Қатты денелердің қарапайым және күрделі қозғалысы

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

Жоспар

І Кіріспе . . . 3

ІІ Негізгі бөлім

Қатты денелердің қарапайым және күрделі қозғалысы

2. 1. Қатты дененің ілгерлемелі қозғалысы және оның қасиеттері . . . 4

2. 2. Қозғалмайтын осьтің төңірегінде қатты дененің айналмалы қозғалысы . . . 6

2. 3. Орташа бұрыштық жылдамдық, айналу жиілігі, бұрыштық үдеу . . . 11

2. 4. Нүктенің салыстырмалы, тасымал және абсолют қозғалыстары . . . 14

2. 5. Жылдамдықтарды қосу туралы теорема . . . 17

2. 6. Үдеулерді қосу туралы теорема . . . 19

Қорытынды . . . 23

Пайдаланған әдебеиттер . . . 24

Кіріспе

Кинематикада статикадағы сияқты абсолют қатты денелер қарастырылады, яғни қозғалыс кезінде дененің кез келген оң нүктесінің арақашықтығы тұрақты болады.

Абсолют қатты дене кинематикасын зерттеу-мынадай мәселелерді қарастырұға келтіріледі:

- қатты дененің қозғалыс түрін анықтау;

- қозғалыстағы қатты дененің кеңістіктен орнын анықтау;

- дененің әр түрлі нүктелерінің траекторияларын анықтай білу;

- дене нүктелерінің жылдамдықтарының өзгеру заңдылығын анықтай

білу;

- дене нүктелерінің үдеулерінің өзгеру заңдылығын анықтай білу. Kейбір жағдайларда кез келген дененің қозғалысын зерттеу барысында оның бip ғана нүктесінің қозғалыс теңдеулері арқылы, дене қозғалысының кинематикалық моделін тұтас беруге болады. Көптеген жағдайда дененің әр бip нүктесінің қозғалыс тендеуі әр түрлі болғандықтан бұлай icтеуге болмайды, сондықтан бip ғана нүктенің кинематикалық параметрлерін білу жеткіліксіз. Бізді қоршап тұрған табиғи ортада қарапайым қозғалыстардан бастап күрделі қозғалыстардың алуан түрлері кездеседі. Енді қатты дененің қарапайым деп саналатын ілгерілмелі және айналмалы қозғалыстарын қарастырайық.

2. 1. Қатты дененің ілгерлемелі қозғалысы және оның қасиеттері

Дененің онымен өзгерместей болып бекітілген түзуі өзінің бастапқы қалпына параллель қалып отыратын қозғалысын ілгерлемелі қозғалыс деп атайды. Мұндай қозғалыста дене нүктелерінің сызатын траекториялары, берілген уақыт мезетіндегі жылдамдықтары мен үдеулері бірдей болады. Мысал ретінде автомобиль қорабының жолдың түзу сызықты бөлігіндегі, велосипед педалінің және 1-суреттен механизмнің ВС буынының қозғалыстарын айтұға болады. Яғни ілгерлемелі қозғалыстағы дене нүктелерінің траекториялары кисық сызықты да болатынын байқаұға болады.

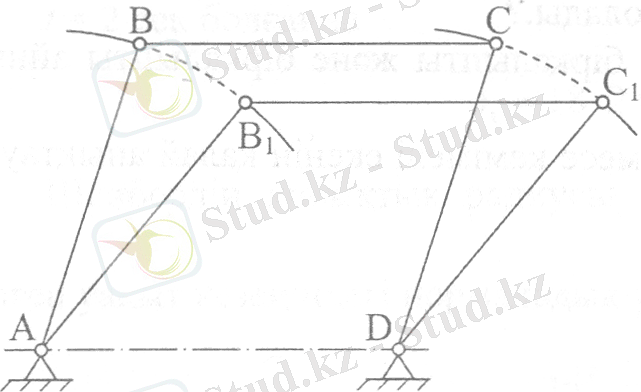
1-сурет

Мысалы велосипедтің АВ педалі (2, а-сурет) қозғалғанда, өзінің бастапқы қалпына параллель қалып отырады, яғни педаль нүктелерінің траекториялары түзу болмаса да педаль үлгерлемелі қозғалыста болады.

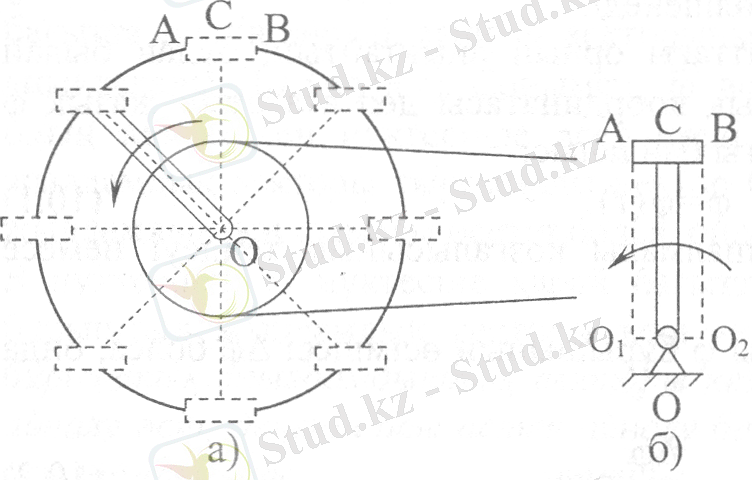
2-сурет

С нүктесінің траекториясы центрі О нүктесінде орналасқан шеңбер болады; сондықтан мысалы басқа А және В нүктелерінің траекториялары да центрлері О ₁ және О ₂ нүктелерінде орналасқан шеңберлер болады. (2, б-сурет) . Бұл шеңберлердің радиустары өзара тең, өйткені олардың траекториялары да бірдей болуы қажет.

Сонымен ілгерлемелі қозғалыста дене нүктелерінің траектоиялары, жылдамдықтары мен үдеулерінің әрбір уақыт кезінде мәндері мен бағыттары бірдей, яғни дене нүктелері конгруентті қозғалыста болады.

2. 2. Қозғалмайтын осьтің төңірегінде қатты дененің айналмалы қозғалысы

Айналмалы қозғалыстың теңдеуі. Дененің бұрыштық, жылдамдығы мен үдеуі. Егер қозғалыстағы дененің кем дегенде екі нүктесі қозғалмайтын болса, онда мұндай дене тұрақты (қозғалмайтын) остен айналмалы қозғалыста болады. Осы қозғалмайтын нүктелер арқылы жүргізілген түзудің барлық нүктелері тыныштық қалпын сақтайды және ол айналу оci деп аталады. Дененің айналу өсінде жатпайтын барлық нүкте траекториялары, центрлері осы осте жататын, ал жазықтықтары осы оске перпендикуляр болатын шеңберлер екенін байқау қиын емес. Енді қозғалмайтын естен айналмалы қозғалатын дененің математкалық моделін құрастырайық. Ол үшін қозғалмайтын естен айналып тұрған дененің (3-сурет) қарастырайық.

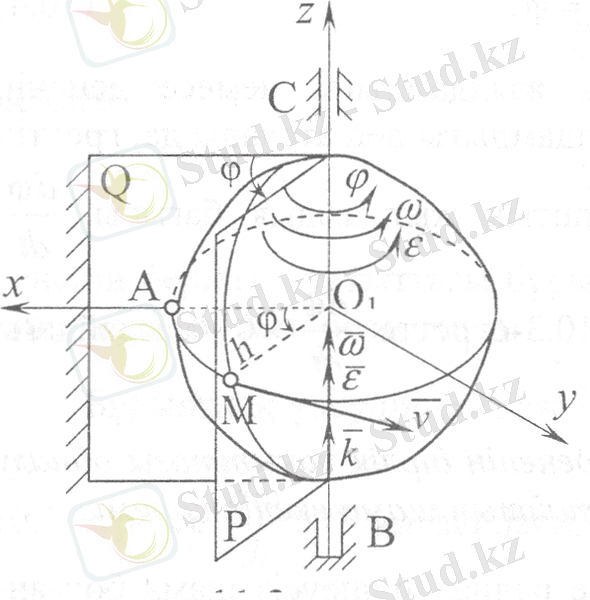
3-сурет

Айналу оci С нүктесінде цилиндрлік подшипникке, В нүктесінде сфералық шарнирге орнатылған. Дененің орны айналу оci арқылы ететін, қозғалмайтын Q және денеге бекітілген Р жарты жазықтықтар арасындағы сәйкес таңбамен алынған eкі жақты φ бұрышымен анықталады. Егер Аz координаталық осінің оң жақ ұшынан қарағанда дененің айналу бағыты сағат тілі айналысына қарама-қарсы болса, онда φ бұрышы оң шама деп, ал дененің айналу бағыты сағат тілі айналуымен бағыттас келсе, онда φ бұрышы тepic шама деп есептелінеді. φ бұрышы әруақытта радианмен өлшенеді.

Дененің кез келген t уақыттағы орнын анықтайтын, бұдан былай айналу бұрышы немесе бұрыштық; координатасы деп аталатын жазық φ бұрышы мен уақыттың арасындағы байланыс:

φ=φ(t) .

дененің қозғалмайтын естен айналмалы қозғалысының теңдеуі немесе айналу заңы болып табылады.

Егер ∆t уақыт аралығындағы φ бұрышының өсімшесі ∆φ болса, онда төмендеп қатынас

$\frac{\mathrm{\Delta}\varphi}{\mathrm{\Delta}t} = \omega_{орт}$

дененің осы уақыт аралығындағы орташа бұрыштық жылдамдығы деп аталады. Осы шаманың ∆t→ 0 шегі, яғни

$\lim_{\mathrm{\Delta}t \rightarrow 0}{}\frac{\mathrm{\Delta}\varphi}{\mathrm{\Delta}t} = \frac{d\varphi}{dt} = \varphi = \omega$

немесе

$\omega = \frac{d\varphi}{dt} = \varphi$

дененің берілген уақыттағы бұрыштық жылдамдығы немесе дененің айналмалы қозғалысының бұрыштық жылдамдығы деп аталады да, гректің Ω, ω (омега) әрпімен белгіленеді. Бұрыштық жылдамдық бағыты $\frac{d\varphi}{dt}$ туындысы таңбасымен анықталады, ал 3-суретте $\frac{d\varphi}{dt} > 0$ жағдайдағы оның оң бағыты көрсетілген.

Сонымен, бұрыштық жылдамдық дененің бірлік уақыттағы айналу бұрышының өзгеру шапшаңдығын сипаттайтын шама екендігін көреміз.

Бұрыштық жылдамдық $\frac{рад}{с}$ немесе радиан өлшеушіс шама болғандықтан $\frac{1}{с}$ пен өлшенеді.

Қатты дененің бұрыштық жылдамдығын айналу өсінің бойымен бағытталатын вектор түрінде қарастырұға болады.

$\overline{\omega} = \omega \bullet \overline{k} = \varphi\overline{k}$ .

мұндағы: $\overline{k}$ - Bz өсінің бойымен бағытталған бірлік орт. Осы $\overline{\omega}$ векторы ұшынан бақылаушы дененің айналуы сағат тип айналуына қарама-қарсы бағытта екенін көреді, яғни $\overline{\omega}$ векторының бағыты оң бұранда ережесімен анықталады (3-сурет) . Сонымен, $\overline{\omega}$ векторы айналу өсінде жатады да, оның кез келген нүктесінде әсер етеді деп саналады, яғни бұрыштық жылдамдық векторы сырғымалы вектор болып табылады. Егер бұрыштық жылдамдықтың шамасы өсетін болса, онда $\overline{\omega}$ векторы айналу оci бойымен В нүктесінен С нүктесіне қарай бағытталады; ал азайатын болса онда бұрыштық жылдамдық векторы кepi қарай бағытталады. Олай болса бұрыштық, жылдамдықтың векторы кез келген уақыт кезеңінде дененің айналу өсі, дененің осы остен айналу бағытын және дененің бұрыштық жылдамдығының модулін анықтайды.

Енді бұрыштық үдеу туралы ұғымды қарастырайық. Егер ∆t уақыт аралығында бұрыштық жылдамдық өсімшесі ∆ω болса, онда

$\frac{\mathrm{\Delta}\omega}{\mathrm{\Delta}t} = \varepsilon_{орт}$

шамасы дененің осы уақыт аралығындағы орташа бұрыштық үдеуі деп аталады. Осы шаманың ∆t → 0 шегі, яғни

$\lim_{\mathrm{\Delta}t \rightarrow 0}{}\frac{\mathrm{\Delta}\omega}{\mathrm{\Delta}t} = \frac{d\omega}{dt} = \varepsilon = \omega$

$\varepsilon = \frac{d\omega}{dt} = \frac{d}{dt}\left( \frac{d\varphi}{dt} \right) = \frac{d^{2}\varphi}{{dt}^{2}} = \varphi$

дененің берілген уақыттағы бұрыштық үдеуі деп аталады да, гректің Е, ε (эпсилон) әрпімен белгіленеді.

Бұрыштық үдеудің бағыты туынды таңбасымен анықталады, ал

3-суретте $\frac{d\omega}{dt} >$ 0 жағдайдағы оң бағыты көрсетілген.

Сонымен, бұрыштық үдеу дененің бірлік уақыттағы бұрыштық жылдамдығының өзгеру шапшаңдығын сипаттайтын шама екенін көреміз.

Бұрыштық үдеудің өлшемі $\frac{рад}{с^{2}}$ немесе $\frac{1}{с^{2}}$ болады.

Бұрыштық үдеуді айналу өсінің бойымен бағытталған $\frac{d\overline{\omega}}{dt} = \overline{\varepsilon}$ векторымен өрнектеуге болады (3-сурет) . Дененің үдемелі айналмалы қозғалысында $\overline{\omega}$ және $\overline{\varepsilon}$ векторлары бағыттас, ал кемімелі қозғалысында қарама-қарсы болады.

Бірқалыпты айналмалы қозғалыс. Егер айналмалы қозғалыстың барлық кезеңінде бұрыштық жылдамдық тұрақты (ω = const ) болса, онда айналмалы қозғалыс бірқалыпты болады. Мұндай қозғалыс тендеуін анықталған интеграл табу арқылы анықтаймыз:

φ = φ ₀ +ωt

мұнда φ ₀ - алғашқы айналу бұрышы (t=0 кезіндегі) .

Бірқалыпты айнымалы айналмалы қозғалыс. Егер айналмалы қозғалыстың барлық кезеңінде бұрыштық үдеу тұрақты (ε = const ) болса, онда айналмалы қозғалыс бірқалыпты айнымалы (үдемелі немесе кемімелі) болады. Бұл айналмалы қозғалыс тендеулерін $\varepsilon = \frac{d\omega}{dt}$ екенін ескере отырын, екі рет анықталған интеграл табу арқылы анықтаймыз:

$\omega = \omega_{0} \pm \varepsilon t$

$\varphi = \varphi_{0} + \omega_{0}t \pm \frac{{\varepsilon t}^{2}}{2}$

мұнда $\omega_{0}$ - бастапқы бұрыштық жылдамдық (t=0 кезіндегі) .

Енді φ айналу бұрышы мен N айналым саны және бұрыштық жылдамдық пен техникада жиі кездесетін айналу жиілігінің $\left( n, \ \frac{айн}{мин} \right)$ араларындағы механика есептен шығаруда пайдаланатын байланыстарды қарастырайық.

Дененің айналу осінде жатпайтын кез келген нүктеге шеңбер бойымен дене өз осінен бір рет айналғанда φ = 2π радианта (360°) бұрылады, ал N айналым санына сәйкес айналу бұрышы

φ = 2π N

Егер дененің бip минуттағы айналу жиілігін $n, \ \frac{айн}{мин}$ деп алсак, онда дененің $\frac{рад}{с}$ пен өлшенетін бұрыштық жылдамдығы

$\omega = \frac{2\pi n}{60} = \frac{\pi n}{30}$

2. 3. Орташа бұрыштық жылдамдық, айналу жиілігі, бұрыштық үдеу

Айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары мен үдеулері айналу z осінен h қашықтығында жататын М нүктесін қарастырайық (4, 5-сурет) . Дене айналғанда М нүктесі радиусы h -қа тең жазықтығы айналу осіне перпендикуляр болатын шеңбер сызады. Бұл шеңбердің О центрі айналу осінде жатады. М нүктесінің өзінің траекториясындағы орнын қозғалмайтын Q жазықтығында (3-сурет) жататын бір А нүктесінен есептелінетін s доғалық координатасымен анықтаймыз. s доғасы есептелуінің оң бағыты ретінде айналу φ бұрышының оң бағыты қабылданады.

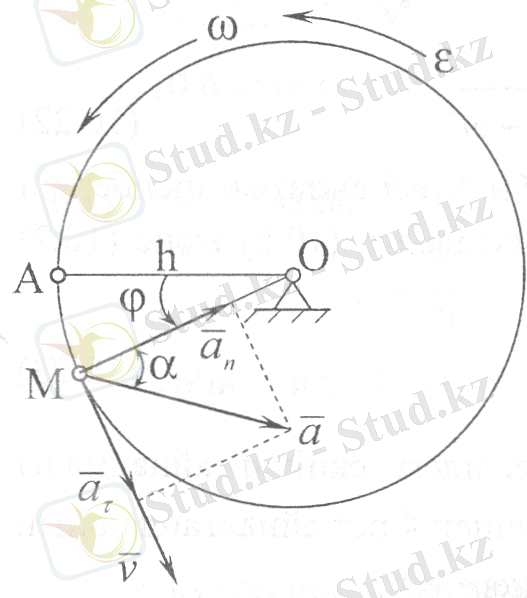
4-сурет

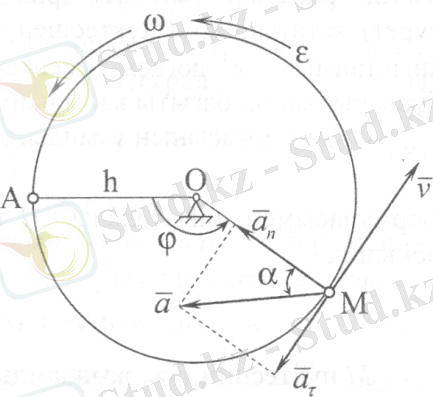
5-сурет

Онда s доғасының ұзындығы

s = h φ = h φ(t)

формуласымен анықталады. М нүктесінің жылдамдығы (9. 26) формула бойынша

$\nu_{М} = \frac{ds}{dt} = h\frac{d\varphi}{dt} = h\omega.$

М нүктесінің осы жылдамдығы нүктенің сызықтық жылдамдығы деп аталады.

Сонымен, айналмалы қозғалыстағы дене нүктесінің сызықтық жылдамдығы дененің бұрыштық жылдамдығы мен нүктенің айналу осіне дейінгі қашықтығының көбейтіндісіне тең. Сызықтық жылдамдық векторы шеңбердің М нүктесінен жүргізілген жанаманың бойымен айналу бағытына қарай бағытталады.

Бұрыштық жылдамдық тұтас дененің кинематикалық сипаттамасы болатындықтан формула бойынша айналмалы қозғалыстағы дене нүктелерінің жылдамдықтары осы нүктелердің айналу өсіне дейінгі қашықтықтарына пропорционал болады.

(9. 32) және (9. 34) формулалары арқылы нүктенің жанама және нормальдық үдеулерін табұға болады:

$a_{\tau} = \frac{dv}{dt} = h\frac{d\omega}{dt} = h\varepsilon$ (10. 15)

$a_{n} = \frac{v^{2}}{\rho} = \frac{\omega^{2}h^{2}}{h} = h\omega^{2}$ (10. 15)

мұнда шеңбер үшін ρ= h

Демек, жанама үдеу векторының модулі:

$\left {\overline{a}}_{\tau} \right = h\left \overline{\varepsilon} \right$

мұнда $\left \overline{\varepsilon} \right$ - бұрыштық үдеудің абсолют шамасы. Дененің үдемелі айналмалы қозғалысында жанама үдеу векторы ${\overline{a}}_{\tau}$ сызықтық жылдамдықтың $\overline{v}$ векторымен бағыттас болады (4-сурет) . Дененің кемімелі айналмалы қозғалысында ${\overline{a}}_{\tau}$ және v векторлары бір-бірiнe қарама-қарсы бағытталады (5-сурет) .

М нүктесінің нормальдық үдеу векторының модулі

$\left {\overline{a}}_{n} \right = a_{n} = h\omega^{2}$

Нормальдық ${\overline{a}}_{n}$ үдеу векторы әрдайым М нүктесі сызатын шеңбер радиусының бойымен айналу осіне қарай бағытталады.

Нүктенің толық үдеу векторының модулі

$a = \sqrt{a_{\tau}^{2} + a_{\tau}^{2}} = h\sqrt{\varepsilon^{2} + \omega^{4}}.$

$\overline{a}$ векторының бағыты осы вектордың М нүктеcі сызатын шеңбердің ОМ радиусымен жасайтын α бұрышымен анықталады. (10. 6) және (10. 7) суреттерден

$tg\alpha = \frac{\left a_{\tau} \right}{a_{n}} = \frac{\varepsilon}{\omega^{2}}$

2. 4. Нүктенің салыстырмалы, тасымал және абсолют қозғалыстары

Осыған дейін нүкте қозғалысы шартты түрде қозғалмайтын деп алынган санақ жүйесінде қарастырылып келді. Көп жағдайда нүкте қозғалысы бірден ең санақ жүйесіне қатысты қарастырылады. Осы санақ жүйелерінің бірi негізгі немесе шартты түрде қозғалмайтын санақ жүйесі деп алынса, екінші (қозғалмалы санақ жүйесі) осы негізгі санақ жүйесіне Қарағанда белгілі бір заңдылықпен қозғалады. Бip мезгілде қозғалмайтын және қозғалмалы санақ жүйелеріне Қарағанда қозғалысы зерттелетін нүктенің немесе дененің қозғалысын күрделі (абсолютты) қозғалыс деп аталады. Мысалы қозғалып бара жаткан су кемесі палубасында домалап бара жатқан шардың жағаға қарағандағы қозғалысын күрделі қозғалыс деп есептеуге болады. Бұл күрделі қозғалыс шардың кемеге (қозғалмалы санақ жүйесіне) қарағандағы қозғалысы мен шардың кемемен біргe жағаға (қозғалмайтын санақ жүйесіне) қарағандағы қозғалысынан құралады. Осылайша шардың күрделі қозғалысы ең қарапайым және оңай зерттелетін қозғалыстарға жіктеледі.

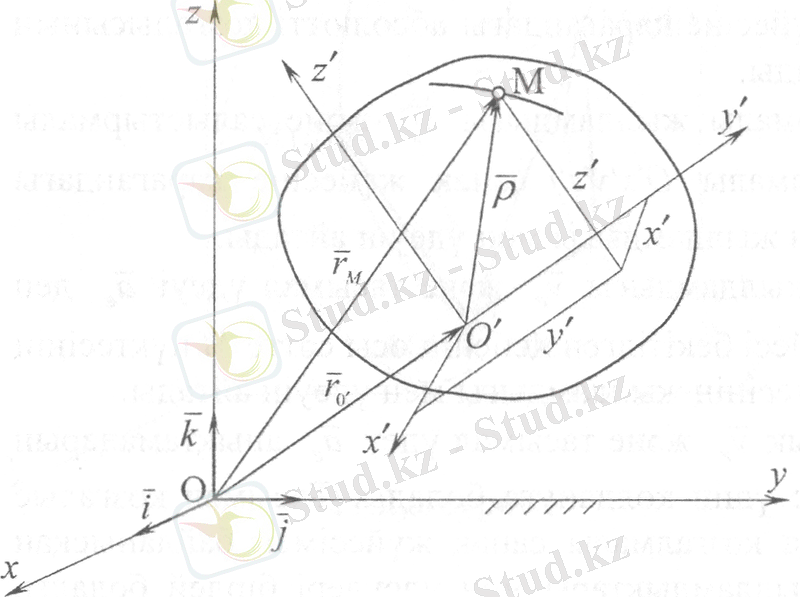
6-сурет

Қозғалмайтын деп алынған Oxyz негізгі санақ жүйесінде, орын ауыстыратын қозғалмалы O'x'y'z' санақ жүйеіне Қарағанда қозғалып бара жатқан М нүктесін (6-сурет) қарастырайық. Осы санақ жүйелерінің әрқайсысы суретте көрсетілмеген белгілі денелермен байланысты болады. Нүктенің қозғалмайтын Oxyz санақ жүйесіне қарағандағы қозғалысын күрделі немесе абсолютті деп, ал O'x'y'z' санақ жүйесіне қарағандағы қозғалысын салыстырмалы қозғалыс деп атаймыз. Қозғалмалы санақ жүйесінің қозғалмайтын санақ жүйесіне қарағандағы қозғалысы бұл нүкте үшін тасымал қозғалыс болады. Олай болса нүктенің осы сәттен тасымал қозғалысын анықтау үшін, дәл осы кезден бастап оны O'x'y'z' қозғалмалы координаталар жүйесіне бекітілген нүкте деп жорамалдауымыз керек, яғни нүкте тек қозғалмалы санақ жүйесімен біргe қозғалады дейміз.

Демек, М нүктесінің тасымал қозғалысы деп қозғалмалы O'x'y'z' санақ жүйесі бекітілген дененің сол сәттен осы М нүктесінің дәл келіп (басып) тұрған нүктесінің қозғалмайтын Oxyz санақ жүйесіне қарағандағы қозғалысын айтамыз.

Нүктенің күрделі қозғалысын зерттеген кезде абсолют, тасымал, салыстырмалы жылдамдықтар және абсолют, тасымал, салыстырмалы үдеулер деген ұғымдар енгізіледі.

М нүктесінің абсолюта жылдамдығы $\overline{v}$ және абсолютті үдеуі $\overline{a}$ деп оның қозғалмайтын санақ жүйесіне қарағандағы абсолютті қозғалысының жылдамдығы мен үдеуін айтады.

М нүктесінің салыстырмалы жылдамдығы $\overline{v}$ _r және салыстырмалы үдеуі $\overline{a}$ _r деп оның қозғалмалы O'x'y'z' санақ жүйесіне қарағандағы салыстырмалы қозғалысының жылдамдығы мен үдеуін айтады.

М нүктесінің тасымал жылдамдығы $\overline{v}$ _e және тасымал үдеуі $\overline{a}$ _e деп қозғалмалы O'x'y'z' санақ жүйесі бекітілген дененің осы сәтте М нүктесінің дәл келіп (басып) тұрған нүктесінің жылдамдығы мен үдеуін айтады.

Осы тасымал жылдамдың $\overline{v}$ _e және тасымал үдеу $\overline{a}$ _e анықтамаларын кез келген тасымал қозғалыс үшін қолдануға болады. Тасымал қозғалыс ілгерлемелі болған жағдайда қозғалмалы санақ жүйесімен байланысқан барлық дене нүктелерінің жылдамдықтары мен үдеулері бірдей болады. Сондықтан тек осы жағдайда ғана қозғалып бара жатқан М нүктесінің тасымал жылдамдығы $\overline{v}$ _e және тасымал үдеуі $\overline{a}$ _e оның қозғалмалы санақ жүйесіне қарағандағы орнына тәуелсіз болады. Демек, бұл жағдайда М нүктесінің тасымал жылдамдығы мен тасымал үдеуі деп қозғалмалы санақ жүйесінің абсолютті жылдамдығы мен абсолютті үдеуін айтуға болады.

Сонымен нүкте күрделі қозғалыста болғанда кинематиканың негізгі мақсаты, нүктенің салыстырмалы және тасымал қозғалыстарын біле отырып оның күрделі қозғалысының жылдамдығы мен үдеуін анықтау болып табылады.

2. 5. Жылдамдықтарды қосу туралы теорема

М нүктесі қозғалмайтын Oxyz санақ жүйесіне қарағандағы қозғалып бара жатқан дененің бетіндеп АВ қисығының бойымен қозғалатын болсын. М нүктесінің күрделі қозғалысы нүктенің АВ қисығының бойындағы салыстырмалы қозғалысы мен нүктенің АВ қисығының денемен біргe Oxyz санақ жүйесіне қатысты тасымалды қозғалысының қосындысына тең.

7-суретте АВ қисығы және қисықтың с орнындағы М нүктесінің орны t уақытына, ал А ₁ В ₁ қисығы және оның D орнындағы нүктенің M ₁ орны t ₁ = t +∆t уақытына сәйкес келеді.

М нүктесі ∆t уақыт аралығында М $\overline{М}$ ₁ абсолют шамасына орын ауыстырады.

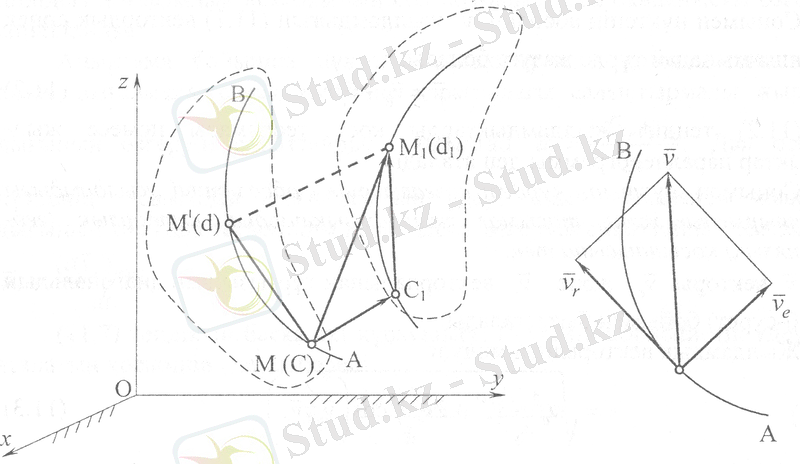
7, а-сурет 7, б-сурет

Нүктенің тасымалды қозғалысындағы орынауыстыруы үшін t уақыт кезеңінде АВ қисығының с орнына дәлме-дәл келетін нүктенің с $\overline{с}$ ₁ = Мс ₁ орынауыстыруы алынады. Нүктенің салыстырмалы қозғалысының орынауыстыруы үшін нүктенің АВ траекториясының бойындағы АВ қисығында анықталатын М $\overline{М}$ ¹ векторы, ал А ₁ В ₁ қисығында с ₁ $\overline{М}$ ₁ векторымен беріледі және М $\overline{М}$ ¹ = с ₁ $\overline{М}$ ₁ .

Мс ₁ М ₁ векторлық үшбұрышынан алатынымыз $\overline{{ММ}_{1}} = \overline{Мс_{1}} + \overline{с_{1}М_{1}}$ . Осы теңдіктің екі жағын ∆t-ға бөліп және ∆ t шексіз нолге ұмтылғандағы жағдайды ескерсек

$\lim_{\mathrm{\Delta}t \rightarrow 0}\frac{{\overline{MM}}_{1}}{\mathrm{\Delta}t} = \lim_{\mathrm{\Delta}t \rightarrow 0}{\frac{{\overline{Mc}}_{1}}{\mathrm{\Delta}t} + \lim_{\mathrm{\Delta}t \rightarrow 0}\frac{{\overline{c_{1}M}}_{1}}{\mathrm{\Delta}t}}$

Анықтамалар бойынша

$\lim_{\mathrm{\Delta}t \rightarrow 0}\frac{{M\overline{M}}_{1}}{\mathrm{\Delta}t} = \overline{v}, \ \lim_{\mathrm{\Delta}t \rightarrow 0}{\frac{{M\overline{c}}_{1}}{\mathrm{\Delta}t}{\overline{v}}_{e}}$

AB қисығы ∆ t шексіз нөлге ұмтылғанда қисығымен беттесуге тырысады, ал М $\overline{М}$ ¹ векторы с ₁ $\overline{М}$ ₁ векторымен дәлме-дәл келеді.

$\lim_{\mathrm{\Delta}t \rightarrow 0}{\frac{\overline{с_{1М_{1{\mathrm{\Delta}t} =}\lim_{\mathrm{\Delta}t \rightarrow 0}{\frac{\overline{{MM}^{1}}}{\mathrm{\Delta}t} = {\overline{v}}_{r}}$