Қатты дененің еркін қозғалысының кинематикасы және қозғалыс теңдеулері


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қазақстандық қазіргі заман “Болашақ” академиясының колледжі
Курстық жұмыс
Пәні: Техникалық механика
Тақырыбы: «Қатты дененің еркін қозғалысы»
Орындаған: Сенбек Ж. Б.
Тобы: ЭРМТ - 12
Тексерген: Бектилеуова С. К.
Ақтау-2014 ж.
Қазақстандық қазіргі заман «Болашақ» академиясы колледжі
КУРСТЫҚ ЖҰМЫСҚА ТАПСЫРМА
пәні бойынша
Студенттің аты - жөні
Тобы
Тақырыбы:
Қолданылатын әдебиеттер:
Берілу мерзімі:
Тапсырылатын мерзімі:
МАЗМҰНЫ
КІРІСПЕ . . . 2
I. ҚАТТЫ ДЕНЕНІҢ ЕРКІН ҚОЗҒАЛЫСЫ
1. 1. Қозғалыс теңдеулері. Дененің еркін қозғалысын ілгерілемелі және сфералық қозғалыстарға жіктеу . 5
1. 2 . Еркін дене нүктелерінің жылдамдықтарын анықтау . . . 7
1. 3 Бұрыштық жылдамдық пен бұрыштық үдеудің таңдап алынған полюске тәуелсіздігі 8
1. 4. Еркін қозғалып бара жатқан дене нүктелерінің үдеулерін анықтау . . . 10
1. 5. Еркін қозғалып бара жатқан дене үшін есептер . . 11
1. 6 Қозғалыс теңдеулері. Дененің еркін қозғалысын ілгерілемелі және сфералық қозғалыстарға жіктеу . . . 16
1. 7 Еркін дене нүктелерінің жылдамдықтарын анықтау . . . 19
1. 8 Бұрыштық жылдамдық пен бұрыштық үдеудің таңдап алынған полюске тәуелсіздігі . . 20
1. 9 Еркін қозғалып бара жатқан дене нүктелерінің үдеулерін анықтау . . . 22
1. 10 Еркін қозғалып бара жатқан дене үшін есептер. 23
ҚОРЫТЫНДЫ . 29
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР . . . 30
КІРІСПЕ
Кинематика (гр. kіnma, kіnmatos - қозғалыс) - механиканың, дене қозғалысының геометриялық қасиеттерін, олардың массасы мен әсер етуші күштерді ескермей зерттейтін бөлімі. Ол дененің неліктен осылай қозғалатынын түсіндірмейді, бірақ "Дене қалай қозғалады?" деген сұраққа жауап береді. Қозғалыс Кинематикасындағы әдістер мен тәуелділіктер әр түрлі механизмдердегі, машиналардағы, т. б. қозғалыстарды есептеуде, сондай-ақ динамика есептерін шешуде пайдаланылады. Соның ішінде қозғалыстың екі түрі болады. Олар: ілгермелі және айнымалы. Ілгермелі қозғалыс - дененің кез-келген екі нүктесін қосатын түзу сызық өзіне-өзі параллель күйде қозғалатын. Мұндай қозғалыс кезінде дененің барлық нүктелері бірдей қозғалады, сондықтан ілгермелі қозғалысты қарастырылады, оның тек бір ғана нүктесінің қозғалысын қарастыру жеткілікті. Бұл жағдайда қозғалысты сипаттау үшін материал нүкте ұғымын қолдануға болады. Механикалық қозғалыс - дегеніміз уақыт туіне қарай дененің немесе оның кейбір бөліктерінің санақ денесі деп аталатын басқа денелерге қатысты кеңістіктегі орын ауыстыруы. Зерттелетін нысанның қасиеттеріне байланысты Кинематика: нүктелер Кинематикасы, қатты денелер Кинематикасы және үздіксіз өзгеріп отыратын орта (деформаланатын денелердің, сұйықтықтардың, газдардың) Кинематика сы болып бөлінеді. Жерге қатысты белгілі бір биіктіктен түсірілген денелер қозғалыс бағытын өзгертпей, вертикаль бағытта жер бетіне жетеді. Жоғарыдан түсірілген дене еркін түсу қозғалысы барысында Жердің тартылысы әсерінен денелер тұрақты және бағыты төменге бағытталған үдеуге ие болады (g=9. 8 м/ 2 ) . Жерге қатысты белгілі бір биіктіктен бастапқы жылдамдықсыз түсірілген дененің Жердің тартылысы әсерінен жасайтын қозғалысы дененің еркін түсуідейміз. Еркін түсу қозғалысын сипаттайтын теңдеулер: h=1/2gt 2 ( t уақытта жүрілген жол), V=gt (t уақыттан кейінгі жылдамдық), V=2gh(Уақытқа тәуелсіз жылдамдық) Дененің шеңбер бойымен өзара тең аралығында бірдей жол жүруі бірқалыпты шеңбер бойымен қозғалыс деп аталады. Дененің шеңбер бойымен қозғалыс барысында дененің бір айналымға жұмсалған уақыты период Т, ал бірлік уақытта жұмсалған айналым саны жиілік ʋ деп аталады . Санақ жүйесі деп санақ дененсінен, онымен байланысқан координаталар жүйесінен және уақыт есептейтін аспаптан тұратын жүйені айтады. Координаталар жүйесі мен санақ жүйесі бір нәрсе емес және оларды шатастыруға болмайды.
Кинематикада кез келген нысанның қозғалысы белгілі бір денемен (санақ денесі) салыстырыла отырып зерттеледі. Қарастырылып отырған нысанның орны, санақ жүйесінің көмегімен, санақ денесі деп аталатын белгілі бір денемен салыстырмалы түрде анықталады. Санақ жүйесі зерттеу мақсатына байланысты алынады. Кинематикада нүктелер мен денелер қозғалысының берілу тәсілі және қозғалыс теңдеулері бойынша қозғалыстың Кинематикалық сипаттамалары (траектория, жылдамдық, үдеу, бұрыштық үдеу, т. б. ) анықталады. Нүктенің қозғалысын сипаттау үшін табиғи, координаттық және векторлық деп аталатын үш тәсілдің бірі пайдаланылады.
I. ҚАТТЫ ДЕНЕНІҢ ЕРКІН ҚОЗҒАЛЫСЫ
1. 1. Қозғалыс теңдеулері. Дененің еркін қозғалысын ілгерілемелі және сфералық қозғалыстарға жіктеу
Дененің кеңістікте қалаған жаққа қозғала алатын мүмкіншілігін оның еркін қозғалысы деп атайды. Мысалы, лақтырылған тастың, зеңбіректен атылған снарядтың, аспанда жасалынатын жоғары ұшу өнерін көрсететін ұшақ қозғалысы және т. т. с. Мысалы, қозғалыс.
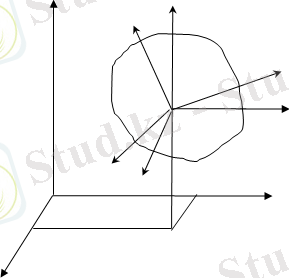
Қозғалмайтын хОуz координаттар жүйесіне қатысты дене еркін қозғалып бара жатқан болсын (2. 1-сурет) . Қозғалып бара жатқан денеге тиісті болған кез келген О 1 нүктені алып ол арқылы екі коодинаттар жүйесін өткізейік. Бірі х 1 О 1 у 1 z 1 денемен байланысты. Екіншісі О 1 xhz. Бұл коодинаттар жүйесінің өстері қозғалмайтын хОуz коодинаттар жүйесінің өстеріне параллель. Онда еркін қозғалып бара жатқан дененің кез келген уақыттағы орнын анықтауға болады, егер қозғалмалы х 1 О 1 у 1 z 1 жүйенің қозғалмайтын хОуz коодинаттар жүйесіне қатысты алатын орны белгілі болатын болса.
z
 z
z
2. 1-сурет
Бұл үшін полюс ретінде алынған О 1 нүктенің кеңістікте алатын орны, яғни х 01 , у 01 , z 01 лердің коодинаттары және сонымен қатар х 1 , у 1 , z 1 өстерінің О 1 xhz коодинаттар жүйесіне қатысты алатын орны белгілі болуы керек. Бұл 12-тарауда келтірілген Эйлер бұрыштары y, j, q арқылы анықталады. Демек, еркін қозғалатын дененің еркіндік дәрежесі 6 ға тең болып оның кеңістіктегі кез келген уақыттағы алатын орны 6 х 01 , у 01 , z 01 , y, j, q параметрлер арқылы табылады. Жалпы жағдайда барлық бұл параметрлер уақытқа байланысты өзгеріп отырады, яғни олар уақытқа тәуелді. Демек, бұл параметрлерді уақыттың функциясы ретінде былай жазуға болады:
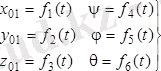 (2. 1)
(2. 1)
(2. 1) өрнектермен анықталатын теңдеулер дененің еркін қозғалысының теңдеулері деп аталады. Бірінші үш теңдеу денеден таңдап алынған О 1 полюс нүктенің қозғалыс теңдеуін береді, яғни дененің еркін қозғалысының ілгерілемелі бөлігі, ал кейінгі үш теңдеу дененің О 1 полюсының төңірегінде оның айналған кездегі сфералық қозғалысын анықтайды. Олай болса жалпы жағдайда дененің еркін қозғалысын екі қозғалысқа жіктеуге болады екен:
- жылдамдығы полюс жылдамдығына тең болған ілгерілемелі қозғалысқа;
- полюс төңірегінде айналудан пайда болатын сфералық қозғалысқа.
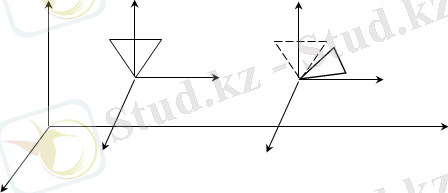
Осындай қорытындыға басқа жолмен де келуге болады. Еркін қозғалып бара жатқан дененің бірер-бір жүйеге қатысты кез келген уақыттағы алатын орнын анықтау үшін бір түзу боында жатпайтын үш нүктенің алатын орындарын білуіміз керек, яғни денемен біріктірілген үшбұрыштың қаралып отырған уақыттағы алатын орны бізге анық болуы шарт (2. 2-сурет) .
 z z
1
z
1
z z
1
z
1
2. 2-сурет
АВС үшбұрышын бір орыннан екінші бір орынға өткізу үшін оған кез келген бір ұшы дәлме-дәл түскенге дейін (мысалы А ұшы) ілгерілемелі көшу өткізіп, содан кейін осы нүктеден өтетін өсь төңірегінде үшбұрышты айландырамыз (2. 2-сурет) .
Полюсті таңдап алғаннан қозғалыстың тек ілгерілемелі бөлігі ғана (х 01 , у 01 , z 01 ) өзгереді, ал айналатын бөлігі (y, j, q) өзгермейді.
1. 2 Еркін дене нүктелерінің жылдамдықтарын анықтау
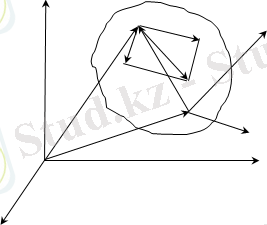
Дене қозғалмайтын хОуz коодинаттар жүйесіне қатысты еркін қозғалып бара жатқан болсын (2. 2-сурет) .
 z
z
2. 2-сурет
О
1
нүктесін полюс ретінде қабылдап дененің кез келген М нүктесінің жылдамдығын анықтайық. Бұл үшін қозғалмайтын О нүктесінен О
1
және М нүктелеріне олардың
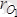 және
және
 радиус-векторларын, ал О
1
полюстен О
1
және М нүктелерді қосатын
радиус-векторларын, ал О
1
полюстен О
1
және М нүктелерді қосатын
 радиус-векторын өткіземіз. Онда
радиус-векторын өткіземіз. Онда
 =
=
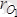 +
+
 .
.
Мұндағы
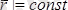 . Себебі еркін қозғалып бара жатқан дене абсолют қатты дене болып есептеледі.
. Себебі еркін қозғалып бара жатқан дене абсолют қатты дене болып есептеледі.
Енді осы өрнекті уақыт бойынша бір рет дифференциалдаймыз, онда
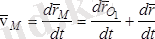 .
.
Бұл жердегі
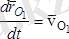 - полюс О
1
дің жылдамдығы;
- полюс О
1
дің жылдамдығы;
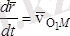 - О
1
полюс төңірегінде айналған кездегі дененің М нүктесінің жылдамдығы. Бұл белгілеулерді еске алсақ, онда
- О
1
полюс төңірегінде айналған кездегі дененің М нүктесінің жылдамдығы. Бұл белгілеулерді еске алсақ, онда
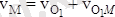 . (2. 2)
. (2. 2)
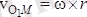 болғандықтан
болғандықтан
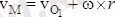 . (2. 3)
. (2. 3)
Сонымен еркін қозғалып бара жатқан дененің кез келген нүктесінің жылдамдығы денеден таңдап алынған полюстың және дене осы полюстың төңірегінде айланған кездегі зерттеліп отырған нүктенің жылдамдықтарының геометриялық қосындысына тең болған шаманы айтады.
1. 3. Бұрыштық жылдамдық пен бұрыштық үдеудің таңдап алынған полюске тәуелсіздігі
Алдын-ала бұрыштық жылдамдық векторының таңдап алынған полюске тәуелсіздігін көрсетейік. Бұл үшін полюс ретінде денеге тиісті оның екі О
1
және О
2
нүктелерін алайық.
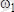 және
және
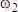 деп осы полюстерден өтетін лездік айналу өсьтеріне қатысты дененің айналу кезіндегі бұрыштық жылдамдықтарының векторларын белгілейік.
деп осы полюстерден өтетін лездік айналу өсьтеріне қатысты дененің айналу кезіндегі бұрыштық жылдамдықтарының векторларын белгілейік.
Осы полюстерден дененің кез келген М нүктесіне
 және
және
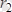 радиус-векторларын жүргізейік. Онда дененің М нүктесінің жылдамдығын былай жазуға болады:
радиус-векторларын жүргізейік. Онда дененің М нүктесінің жылдамдығын былай жазуға болады:
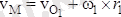 ,
,
немесе
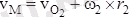 .
.
Бұл өрнектерді өзара теңестіріп табатынымыз:
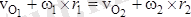 .
.
Егер дененің О
1
нүктесін полюс ретінде қарастырсақ, онда
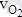 мен
мен
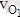 векторлардың арасындағы төмендегідей байланысты анықтаймыз:
векторлардың арасындағы төмендегідей байланысты анықтаймыз:
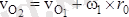
Бұл жердегі
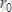 - О
2
полюсының О
1
полюске қатысты радиус-векторы.
- О
2
полюсының О
1
полюске қатысты радиус-векторы.
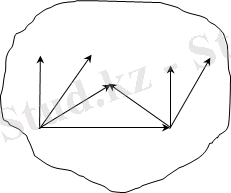
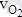 ның өрнегін алдыңғы теңдікке
ның өрнегін алдыңғы теңдікке
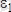 апарып қойсақ, онда
апарып қойсақ, онда
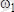
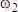
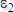
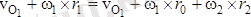

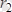 немесе
немесе
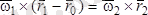
О
1
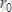 О
2
О
2
Бірақ
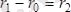 , олай болса:
, олай болса:
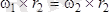 .
.
немесе
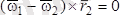
Ақырғы теңдік кез келген r 2 үшін орынды болғандықтан, бұдан
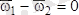
келіп шығады. Ендеше
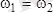
Сонымен бұрыштық жылдамдықтың шамасы денеден таңдап алынған полюске байланысты емес. Ал бұрыштық үдеудің де денеден таңдап алынған полюске байланысты емес екенін көрсету үшін ақырғы өрнектің екі жағын
бірдей дифферециалдаймыз. Бұдан табатынымыз:
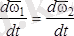 немесе
немесе
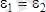
яғни бұрыштық үдеу де полюстың қалай таңдалғанына байланысты емес екен.
1. 4. Еркін қозғалып бара жатқан дене нүктелерінің үдеулерін анықтау
Еркін қозғалып бара жатқан дененің кез келген М нүктесінің үдеуін анықтау үшін оның жылдамдық
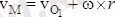 векторын уақыт бойынша дифференциалдаймыз, яғни .
векторын уақыт бойынша дифференциалдаймыз, яғни .
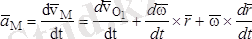
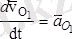 - полюстың жылдамдығы,
- полюстың жылдамдығы,
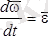 ,
,
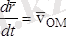 екендерін еске алсақ, онда
екендерін еске алсақ, онда
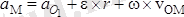
келіп шығады.
Бұл жердегі
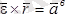 - М нүктенің О полюстен өтетін бұрыштық үдеу өсіне қатысты айналу үдеуі;
- М нүктенің О полюстен өтетін бұрыштық үдеу өсіне қатысты айналу үдеуі;
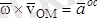 - М нүктесінің О полюстен өтетін лездік айналу өсі Р ға қатысты алынған өське тартқыш үдеуі.
- М нүктесінің О полюстен өтетін лездік айналу өсі Р ға қатысты алынған өське тартқыш үдеуі.
Демек,
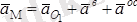 .
.
Бұл өрнек еркін қозғалатын дене үшін Ривальс теоремасын береді
Сонымен еркін дененің үдеуі үш үдеудің геометриялық қосындысынан тұрады. Олар: полюстің үдеуі, О полюстен өтетін бұрыштық үдеу өсіне қатысты айналу үдеуі; О полюстен өтетін лездік айналу өсі Р ға қатысты алынған өське тартқыш үдеуі.
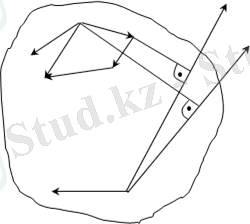

М
2. 4-сурет
Олай болса еркін қозғалатын дененің кез келген нүктесінің үдеуі үдеулердің көпбұрыштарын құрумен анықталады екен (13. 4-сурет) .
1. 5 Еркін қозғалып бара жатқан дене үшін есептер
2. 1-есеп.
Еркін қозғалып бара жатқан дененің А нүктесінің жылдамдық векторы
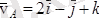 (v
A
-өлшем бірлігі м/сек), бұрыштық жылдамдық векторы
(v
A
-өлшем бірлігі м/сек), бұрыштық жылдамдық векторы
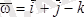 (w-өлшем бірлігі рад/сек) және М нүктесінің А нүктеге қатысты радиус-векторы
(w-өлшем бірлігі рад/сек) және М нүктесінің А нүктеге қатысты радиус-векторы
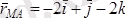 (
(
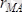 -өлшем бірлігі метр) белгілі болсын. Дененің М нүктесінің жылдамдығы анықталсын.
-өлшем бірлігі метр) белгілі болсын. Дененің М нүктесінің жылдамдығы анықталсын.
Шешуі. А нүкте жылдамдығының қозғалмайтын координаттар өстеріне болған проекциялары v Ax = 2 м/с, v Ay = -1 м/с, v Az = 1 м/с тең. Ал бұрыштық жылдамдықтың осы қозғалмайтын координаттар өстеріне болған проекциялары:
w х = 1 рад/с, w у = 2 рад/с, w z = -1 рад/с.
Радиуса-вектор
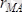 ның осы өстерге болған проекциялары:
ның осы өстерге болған проекциялары:
(
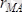 )
х
= -2 м, (
)
х
= -2 м, (
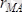 )
у
= 1 м, (
)
у
= 1 м, (
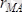 )
z
= -2 м.
)
z
= -2 м.
Олай болса М нүкте жылдамдығының қозғалмайтын координаттар өстеріне болған проекциялары:
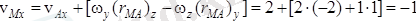 м/с,
м/с,
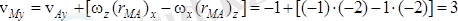 м/с,
м/с,
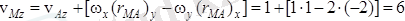 м/с.
м/с.
Ендеше М нүкте жылдамдылығының модулі
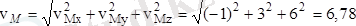 м/с.
м/с.
тең болып шығады.
2. 2-есеп.
Қ
озғалмайтын хОуz санақ жүйесіне қатысты
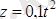 (z - өлшем бірлігі метр, t - секунд) заңға бойсынып лифт вертикал қозғалып бара жатқан болсын. Лифт кабинасының ішінде горизонталь жазықтық бойлап биіктігі О
1
С = 0, 2 м, ұшы ÐАО
1
В = 60
0
бұрышты құраған дөңгелек конус лифтпен байланысты болған х
1
О
1
у
1
z
1
өстер жүйесіне тиісті О
1
z
1
вертикаль өсінің төңірегінде бұрыштық жылдамдығы w = 2 рад/с тең болып бірқалыпты сырғанамай дөңгелейді. Конустың О
1
нүктесі лифтің кабинасымен салыстырғанда қозғалмайды.
Қ
озғалмайтын хОуz санақ жүйесіне қатысты t
1
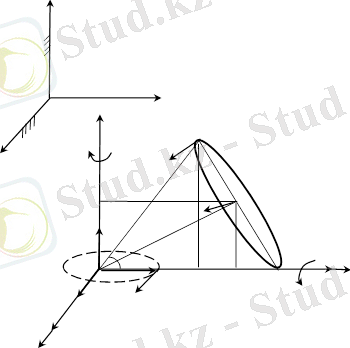
= 1 c болған сәттегі конустың С, А, В нүктелерінің жылдамдықтары және В мен С нүктелерінің үдеулері табылсын (13. 5-сурет) .
(z - өлшем бірлігі метр, t - секунд) заңға бойсынып лифт вертикал қозғалып бара жатқан болсын. Лифт кабинасының ішінде горизонталь жазықтық бойлап биіктігі О
1
С = 0, 2 м, ұшы ÐАО
1
В = 60
0
бұрышты құраған дөңгелек конус лифтпен байланысты болған х
1
О
1
у
1
z
1
өстер жүйесіне тиісті О
1
z
1
вертикаль өсінің төңірегінде бұрыштық жылдамдығы w = 2 рад/с тең болып бірқалыпты сырғанамай дөңгелейді. Конустың О
1
нүктесі лифтің кабинасымен салыстырғанда қозғалмайды.
Қ
озғалмайтын хОуz санақ жүйесіне қатысты t
1
= 1 c болған сәттегі конустың С, А, В нүктелерінің жылдамдықтары және В мен С нүктелерінің үдеулері табылсын (13. 5-сурет) .
Шешуі. 1. С нүктенің жылдамдығын анықтау. Қөзғалмайтын лифтегі конустың сырғанамай домалауы сфералық қозғалыс. Себебі конустың ұшы болып есептелетін О 1 нүктесі қозғалмайды. Қ озғалмайтын лифт ішіндегі конустың домалауы еркін қозғалыс деп есептеледі. Онда конустың өсінде жатқан С нүктенің жылдамдығы төмендегідей формуламен анықталады:
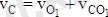 .
.
 z
z
2. 5-сурет
Бұл жердегі
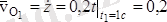 м/с-полюстың жылдамдығы (
м/с-полюстың жылдамдығы (
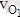 вертикаль жоғары бағытталған),
вертикаль жоғары бағытталған),
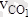 - полюс төңірегінде С нүктенің айналуынан пайда болған жылдамдық.
- полюс төңірегінде С нүктенің айналуынан пайда болған жылдамдық.
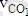 жылдамдығын төмендегідей жолмен табамыз:
жылдамдығын төмендегідей жолмен табамыз:
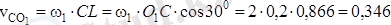 см/с.
см/с.
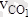 векторы горизонтал жазықтықта жатып, оған қарай бағытталады.
векторы горизонтал жазықтықта жатып, оған қарай бағытталады.
Егер
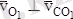 екенін еске алсақ, онда С нүктесінің жылдамдығының модулі:
екенін еске алсақ, онда С нүктесінің жылдамдығының модулі:
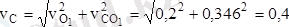 м/с.
м/с.
2. Конустың бұрыштық жылдамдығын анықтау.
Конустың сфералық қозғалысы оның лездік айналу өсінің төңірегіндегі айналуынан тұрады. Конустың лездік өсі О 1 Р оның қозғалмайтын лифтпен жанасатын О 1 В құраушысымен дәлме-дәл келеді. Модуль угловой скорости вращения Конустың лездік өсінің төңірегінде айналуынан пайда болатын бұрыштық жылдамдығының модулі мынадай формуламен табылады:
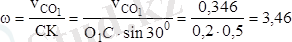 рад/с
рад/с
(СК - С нүктесінен лездік айналу өсіне дейінгі ең жақын арақашықтық) . w векторы лездік айналу өсі О 1 Р бойлап бағытталады (13. 6) .
3. В нүктенің жылдамдығын анықтау
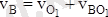 .
.
Бірақ
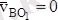 , себебі В нүктесі лездік айналу өсінде жатыр. Сондықтан да
, себебі В нүктесі лездік айналу өсінде жатыр. Сондықтан да
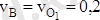 м/с.
м/с.
4. А нүктенің жылдамдығын анықтау
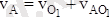 ,
,
мұндағы
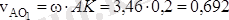 м/с,
м/с,
Сонымен қатар
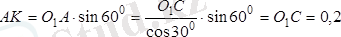 м.
м.
Егер
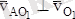 екенін еске алсақ, онда А нүктесінің жылдамдығының модулі:
екенін еске алсақ, онда А нүктесінің жылдамдығының модулі:
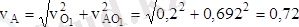 м/с.
м/с.
тең.
5. Конустың бұрыштық үдеуін анықтау.
Конустың бұрыштық жылдамдығының годографын түзейік. w ның модулі өзгермейтін болғандықтан (конустың шайқалуы бірқалыпты), оның
 векторының ұшы горизонтал жазықтық үстінде шеңберді сызады.
векторының ұшы горизонтал жазықтық үстінде шеңберді сызады.
 векторы геометриялық тұрғыдан
векторы геометриялық тұрғыдан
 векторының ұшы ие болатын
векторының ұшы ие болатын
 жылдамдығының модуліне тең (13. 5) . Қаралып отырған жағдайда
жылдамдығының модуліне тең (13. 5) . Қаралып отырған жағдайда
 О
1
z өсінің төңірегіндегі конустың айналу жылдамдығына тең. Онда
О
1
z өсінің төңірегіндегі конустың айналу жылдамдығына тең. Онда
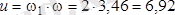 рад/с
2
.
рад/с
2
.
Бұрыштық үдеу
 . Олай болса, оның модулі
. Олай болса, оның модулі
 = 6, 92 рад/с
2
.
= 6, 92 рад/с
2
.
 векторы О
1
нүктеден басталып
векторы О
1
нүктеден басталып
 жылдамдықтың бойымен бағытталады, яғни ол горизонтал жазықтықта жатып
жылдамдықтың бойымен бағытталады, яғни ол горизонтал жазықтықта жатып
 векторына перпендикуляр.
векторына перпендикуляр.
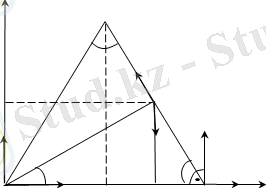
6. Внүктенің үдеуін анықтау
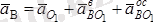 .
.
Бұл жердегі
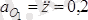 м/с
2
,
м/с
2
,
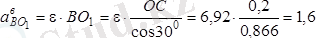 м/с
2
,
м/с
2
,
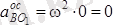 .
.
 z
1
z
1
А
2. 6-сурет
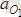 және
және
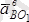 үдеулердің бағыттары 13. 6-суретте көрсетілген. Бұл үдеулер бір-біріне параллель және өзара бағыттас болғандықтан, онда В нүкте үдеуінің модулі
үдеулердің бағыттары 13. 6-суретте көрсетілген. Бұл үдеулер бір-біріне параллель және өзара бағыттас болғандықтан, онда В нүкте үдеуінің модулі
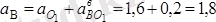 м/сек
м/сек
тең.
7. С нүктенің үдеуін анықтау.
Ол мына формула арқылы табылады, яғни
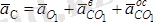
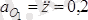 м/с
2
,
м/с
2
,
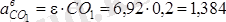 м/с
2
,
м/с
2
,
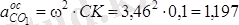 м/с
2
.
м/с
2
.
Мұндағы векторлық теңдеуді у 1 және z 1 өстеріне проекцияласақ, онда:
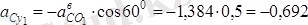 см/с
2
,
см/с
2
,
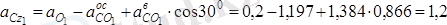 см/с
2
см/с
2
келіп шығады. Олай болса, С нүктенің үдеуінің модулі
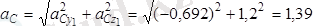 см/с
2
см/с
2
тең.
1. 6 Қозғалыс теңдеулері. Дененің еркін қозғалысын ілгерілемелі және сфералық қозғалыстарға жіктеу
Дененің кеңістікте қалаған жаққа қозғала алатын мүмкіншілігін оның еркін қозғалысы деп атайды . Мысалы, лақтырылған тастың, зеңбіректен атылған снарядтың, аспанда жасалынатын жоғары ұшу өнерін көрсететін самолет қозғалысы және т. т. Мысалы, қозғалыс. Қозғалмайтын хОуz коодинаттар жүйесіне қатысты дене еркін қозғалып бара жатқан болсын(13. 1-сурет) . Қозғалып бара жатқан денеге тиісті болған кез келген О 1 нүктені алып ол арқылы екі коодинаттар жүйесін өткізейік. Бірі х 1 О 1 у 1 z 1 денемен байланысты. Екіншісі О 1 xhz. Бұл коодинаттар жүйесінің өстері қозғалмайтын хОуz коодинаттар жүйесінің өстеріне параллель. Онда еркін қозғалып бара жатқан дененің кез келген уақыттағы орнын анықтауға болады, егер қозғалмалы х 1 О 1 у 1 z 1 жүйенің қозғалмайтын хОуz коодинаттар жүйесіне қатысты алатын орны белгілі болатын болса.
 z
z

z 1
2. 1-сурет
Бұл үшін полюс ретінде алынған О 1 нүктенің кеңістікте алатын орны, яғни х 01 , у 01 , z 01 лердің коодинаттары және сонымен қатар х 1 , у 1 , z 1 өстерінің О 1 xhz коодинаттар жүйесіне қатысты алатын орны белгілі болуы керек. Бұл 12-тарауда келтірілген Эйлер бұрыштары y, j, q арқылы анықталады. Демек, еркін қозғалатын дененің еркіндік дәрежесі 6 ға тең болып оның кеңістіктегі кез келген уақыттағы алатын орны 6 х 01 , у 01 , z 01 , y, j, q параметрлер арқылы табылады. Жалпы жағдайда барлық бұл параметрлер уақытқа байланысты өзгеріп отырады, яғни олар уақытқа тәуелді. Демек, бұл параметрлерді уақыттың функциясы ретінде былай жазуға болады:
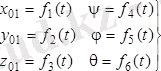 (2. 1)
(2. 1)
(2. 1) өрнектермен анықталатын теңдеулер дененің еркін қозғалысының теңдеулері деп аталады. Бірінші үш теңдеу денеден таңдап алынған О 1 полюс нүктенің қозғалыс теңдеуін береді, яғни дененің еркін қозғалысының ілгерілемелі бөлігі, ал кейінгі үш теңдеу дененің О 1 полюсының төңірегінде оның айналған кездегі сфералық қозғалысын анықтайды. Олай болса жалпы жағдайда дененің еркін қозғалысын екі қозғалысқа жіктеуге болады екен:
1) жылдамдығы полюс жылдамдығына тең болған ілгерілемелі қозғалысқа;
2) полюс төңірегінде айналудан пайда болатын сфералық қозғалысқа.
Осындай қорытындыға басқа жолмен де келуге болады. Еркін қозғалып бара жатқан дененің бірер-бір жүйеге қатысты кез келген уақыттағы алатын орнын анықтау үшін бір түзу боында жатпайтын үш нүктенің алатын орындарын білуіміз керек, яғни денемен біріктірілген үшбұрыштың қаралып отырған уақыттағы алатын орны бізге анық болуы шарт(2. 2-сурет) .
 z z
1
z
1
z z
1
z
1
2. 2-сурет
АВСүшбұрышын бір орыннан екінші бір орынға өткізу үшін оған кез келген бір ұшы дәлме-дәл түскенге дейін (мысалы А ұшы) ілгерілемелі көшу өткізіп, содан кейін осы нүктеден өтетін өсь төңірегінде үшбұрышты айландырамыз (2. 2-сурет) .
Полюсті таңдап алғаннан қозғалыстың тек ілгерілемелі бөлігі ғана (х 01 , у 01 , z 01 ) өзгереді, ал айналатын бөлігі (y, j, q) өзгермейді.
1. 7 Еркін дене нүктелерінің жылдамдықтарын анықтау
Дене қозғалмайтын хОуz коодинаттар жүйесіне қатысты еркін қозғалып бара жатқан болсын (13. 2-сурет) .
 z
z
2. 2-сурет
О
1
нүктесін полюс ретінде қабылдап дененің кез келген М нүктесінің жылдамдығын анықтайық. Бұл үшін қозғалмайтын О нүктесінен О
1
және М нүктелеріне олардың
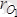 және
және
 радиус-векторларын, ал О
1
полюстен О
1
және М нүктелерді қосатын
радиус-векторларын, ал О
1
полюстен О
1
және М нүктелерді қосатын
 радиус-векторын өткіземіз. Онда
радиус-векторын өткіземіз. Онда
 =
=
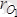 +
+
 .
.
Мұндағы
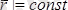 . Себебі еркін қозғалып бара жатқан дене абсолют қатты дене болып есептеледі.
. Себебі еркін қозғалып бара жатқан дене абсолют қатты дене болып есептеледі.
Енді осы өрнекті уақыт бойынша бір рет дифференциалдаймыз, онда
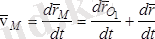 .
.
Бұл жердегі
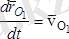 - полюс О
1
дің жылдамдығы;
- полюс О
1
дің жылдамдығы;
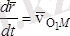 - О
1
полюс төңірегінде айналған кездегі дененің М нүктесінің жылдамдығы. Бұл белгілеулерді еске алсақ, онда
- О
1
полюс төңірегінде айналған кездегі дененің М нүктесінің жылдамдығы. Бұл белгілеулерді еске алсақ, онда
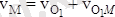 . (2. 2)
. (2. 2)
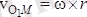 болғандықтан
болғандықтан
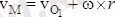 . (2. 3)
. (2. 3)
Сонымен еркін қозғалып бара жатқан дененің кез келген нүктесінің жылдамдығы денеден таңдап алынған полюстың және дене осы полюстың төңірегінде айланған кездегі зерттеліп отырған нүктенің жылдамдықтарының геометриялық қосындысына тең болған шаманы айтады.
1. 8 Бұрыштық жылдамдық пен бұрыштық үдеудің таңдап алынған полюске тәуелсіздігі
Алдын-ала бұрыштық жылдамдық векторының таңдап алынған полюске тәуелсіздігін көрсетейік. Бұл үшін полюс ретінде денеге тиісті оның екі О
1
және О
2
нүктелерін алайық.
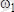 және
және
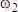 деп осы полюстерден өтетін лездік айналу өсьтеріне қатысты дененің айналу кезіндегі бұрыштық жылдамдықтарының векторларын белгілейік.
деп осы полюстерден өтетін лездік айналу өсьтеріне қатысты дененің айналу кезіндегі бұрыштық жылдамдықтарының векторларын белгілейік.
Осы полюстерден дененің кез келген М нүктесіне
 және
және
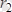 радиус-векторларын жүргізейік. Онда дененің М нүктесінің жылдамдығын былай жазуға болады:
радиус-векторларын жүргізейік. Онда дененің М нүктесінің жылдамдығын былай жазуға болады:
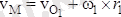 ,
,
немесе
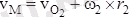 .
.
Бұл өрнектерді өзара теңестіріп табатынымыз:
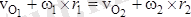 .
.
Егер дененің О
1
нүктесін полюс ретінде қарастырсақ, онда
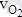 мен
мен
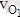 векторлардың арасындағы төмендегідей байланысты анықтаймыз:
векторлардың арасындағы төмендегідей байланысты анықтаймыз:
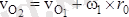
Бұл жердегі
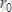 - О
2
полюсының О
1
полюске қатысты радиус-векторы.
- О
2
полюсының О
1
полюске қатысты радиус-векторы.

н
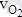 ың өрнегін алдыңғы теңдікке
ың өрнегін алдыңғы теңдікке
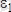 апарып қойсақ, онда
апарып қойсақ, онда
- .

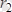 Немесе
Немесе
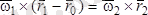 .
.
О
1
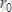 О
2
О
2
Бірақ
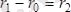 , олай болса:
, олай болса:
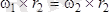 .
.
2. 3-сурет Немесе
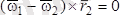 .
.
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz