Транспорттық есеп: математикалық модельдеу, оңтайландыру әдістері және программалық жүзеге асыру


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Техникалық кибернетика кафедрасы
Курстық жұмыс
ТРАНСПОРТТЫҚ ЕСЕП
Тексерген:
Орындаған:
Мазмұны:
Кіріспе . . . 4
1 Қарапайым актілерді белгілеп көрсету . . . 5
2 Жалпы математикалық модельді құру, мақсатты функцияны таңдау және негіздеу . . . 5
3 Алгоритмнің маңызды ойын баяндау . . . 5
3. 1 Солтүстік-батыс және минималдау әдісі . . . 6
3. 2 Потенциалдау әдісі . . . 6
4 Оңтайландыру есебінің айқын математикалық өрнегінің өңделіп, жетілдіруі, оның сандық түрдегі шешімі . . . 7
5 Программа листингісі . . . 12
Программаны баяндау бөлімі . . . 22
Қорытынды . . . 23
Қолданылған әдебиеттер . . . 24
Қосымшалар . . . 25
Есептің қойлымы
Үш А1, А2, А3 теміржол станцияларында 120, 110, және 130 жүк тиелген вагондар
тұрып қалды. Бұл вагондар міндетті түрде В1, В2, В3, В4, В5 темір жол бекеттерінежіберу керек.
2 4 1 6 7
С= 3 3 5 4 2
8 9 6 3 4
Бекеттерге әр вагонның қажеттілігі 80, 60, 70, 100 және 50. А2 теміржол бекетінен В2 және В4 бекеттеріне вагондарды жеткізу мүмкін еместігін ескеріп және бір вагонның жеткізу тарифы С матрицасымен анықталатынын біле тұра, тасымалдаудың жалпы құны сіз болатын жоспарды құру керек.
Кіріспе
Электронды есептеуіш машинаның шығуымен байланысты жаңа ғылыми-техникалық революция ғылымның жаңа даму бағытын орнатты. Осындай бағыттардың бірі - операцияны зерттеу ғылымы.
Операция дегеніміз - белгілі мақсатқа жеткізетін және нақты ниетпен біріктірілген шаралар жиынтығы. Операциялар: басқарылатын және басқарылмайтын болады.
Операцияны зерттеу дегеніміз - автоматтандырылған басқару жүйесіндегі басқару есептерін шешуге қолданатын ғылыми тәсіл. Операцияны зерттеу методологиясы негізгі мына топтарға бөлінеді:
- анықтамалар, кезеңдер, принциптер, есептер;
- операцияны зерттеудің математикалық әдістері. Оған сызықтық бағдарламалау, транспорттық, дискреттік бағдарламалау, бейсызықтық бағдарламалау, динамикалық бағдарламалау, ойындар теориясы кіреді;
- АБЖ жобалау кезіндегі операцияларды зерттеудің әдістерін қолдану. Онда АБЖ-ң алгоритмін қамтамасыз ету, информациямен АБЖ-ны қамтамасыз ету, техникалық қамтамасыз ету керек.
Сызықтық программалау, практикаға маңызды сызықтық функцияның, сызықтық теңсіздіктер немесе теңдеулер түріндегі шектеулердің бар болу кезіндегі максимумын (минимумын) табу, экстремумдық есептерді шешудің классикалық әдістері қажет болмай қалған есебін зерттейді.
Қазіргі уақытқа дейін сызықтық программалаудың ең қарапайым есептерінің бірі, кең тарағаны - транспорттық есеп. Яғни, жүктердің жіберу пункттерінен олардың бару пункттеріне біріктірудің, жүкті тасымалдаудың шығын бағасы минимиза-цияланатын есеп. Оны шешу үшін сызықтық программалау есептерінің барлығына ортақ симплекс әдісінен кішірек болатын сызықтық программалаудың арнайы әдістері қолданылады. Транспорттық есепті шешудің ең танымал әдістеріне потен-циал, солтүстік-батыс, минимал элемент әдістері жатады.
1 Қарапайым актілерді белгілеп көрсету
- а) Үш теміржол станцияларындағы жүктердің шектілігі ескеру (A1, A2, A3) .
- ә) В1, В2, В3, В4, В5 темір жол бекеттеріне қажетті жүктермен қамтамасыз ету.
- б) А2 темір жол бекетінен В2, В4 темір жол бекетіне жүкті жеткізу мүмкін еместігін ескеру.
- в) Тасымалдау құныныңаз болуын қамтамасыз ету.
2 Жалпы математикалық модельді құру, мақсатты функцияны таңдау және негіздеу
Келесі белгілеуді енгізейік:
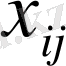 - i карьерінен j құрылыс алаңына жіберілетін құмның мөлшері.
- i карьерінен j құрылыс алаңына жіберілетін құмның мөлшері.
 - карьердің номері;
- карьердің номері;
 - құрылыс алаңның номері;
- құрылыс алаңның номері;
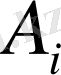 - i-ші карьерден жіберілетін құмның мөлшері;
- i-ші карьерден жіберілетін құмның мөлшері;
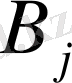 - j-ші құрылыс алаңына қажет құмның мөлшері;
- j-ші құрылыс алаңына қажет құмның мөлшері;
Мақсатты функция келесі түрде болады:
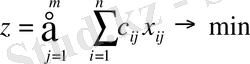
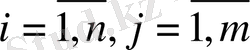
Карьердегі құм толығымен тасылуы керек:
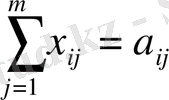
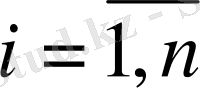
Құрылыс алаңы толығымен қамтамасыз етілуі керек:
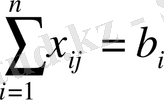
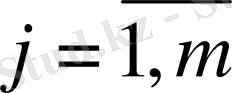

3 Алгоритмнің маңызды ойын баяндау
Транспорттық есеп дегеніміз - тасымалдау құны ең аз болатын жүктерді жіберу пунктерінен қабылдау пунктеріне тасымалдау.
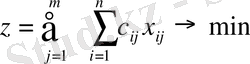 (1)
(1)
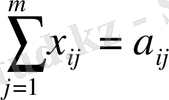 (2)
(2)
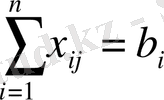 (3)
(3)
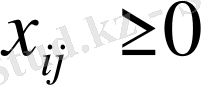 (4)
(4)
Есепті қарастырсақ, онда (1) мақсатты функция транспорт шығынының минимумын көрсетеді. (2) шектеулер жіберу пунктерінің өндіріс қуатының шектілігін ескертеді. (3) шектеулер тұтынушылардың сұраныстарын толық қамтамасыз етуді көрсетеді. Егер
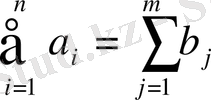 болса, онда (1) -(4) есеп жабық транспорт есебі деп аталады, қарсы жағдайда ашық транспорт есебі деп аталады. Ашық транспорт есебін жабық қылуға болады, ол үшін жалған пунктілер енгізу керек. Жалған пунктінің тасымалдау құны нольге тең.
болса, онда (1) -(4) есеп жабық транспорт есебі деп аталады, қарсы жағдайда ашық транспорт есебі деп аталады. Ашық транспорт есебін жабық қылуға болады, ол үшін жалған пунктілер енгізу керек. Жалған пунктінің тасымалдау құны нольге тең.
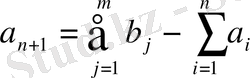
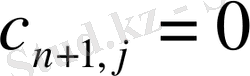
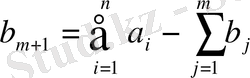
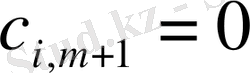
Бұл есепті шешудің көптеген әдістері бар: солтүстік-батыс, минималды элемент, потенциалдар әдісі.
3. 1 Солтүстік-батыс және минималды элемент әдісі
Солтүстік-батыс әдісі деп аталатын себебі, үлестіруді солтүстік-батыс жағынан бастайды.
Минималды элемент әдісі деп аталатын себебі, кестенің ең кіші тасымалдау құны (
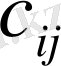 ) тұрған тордан бастайды.
) тұрған тордан бастайды.
Бұл екі әдіс транспорттық есептің тіректі жоспарын табу үшін қолданады. Есеп әрі қарай потенциалдау әдісімен есептеледі.
3. 2 Потенциалдау әдісі
Транспорт есебін потенциалдар әдісімен шығаруға болады. Потенциалдар әдісі тек қана жабық транспорт есебінде қолданылады. Потенциалдар әдісін қолдану үшін тіке транспорт есебіне қосмағыналы есебін құру керек.
Потенциалдар әдісінің алгоритмі:
Алғашқы қадам.
- Басты жоспарды құру.
- Жоспары бар торлар үшінжүйесін жасау.
- Жоспары жоқ торлардың потенциалдығын зерттеу -
Алғашқы қадам бір-рет орындалады.
Жалпы қадам.
- Жоспарды одан да жақсарту.
- Жүйені түзету.
- Түзетілген жүйенің потенциалдығын зерттеу.
Алғашқы жоспар не солтүстік-батыс бұрыш әдісімен, не минималды элемент әдісімен жасалады.
Жоспары бар торларға
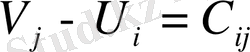 жүйесі жасалады. Жоспары жоқ торларға
жүйесі жасалады. Жоспары жоқ торларға
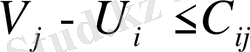 теңсіздіктер жүйесі құралады. Егер бұл шарттар орындалмаса, онда
теңсіздіктер жүйесі құралады. Егер бұл шарттар орындалмаса, онда
 ізделінеді. Табылған барлық
ізделінеді. Табылған барлық
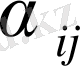 -лардың ішінен ең үлкені
-лардың ішінен ең үлкені
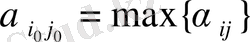 болып алынады.
болып алынады.
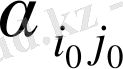 тордан бастап, жоспары бар торларды сағат тіліне қарсы бағыт бойынша цикл құрылады. Сонымен бірге
тордан бастап, жоспары бар торларды сағат тіліне қарсы бағыт бойынша цикл құрылады. Сонымен бірге
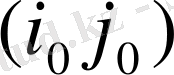 тордан бастап, цикл бұрылатын жерде алма кезек «+», «-» белгілері қойылады. «-» (минуста) тұрған барлық
тордан бастап, цикл бұрылатын жерде алма кезек «+», «-» белгілері қойылады. «-» (минуста) тұрған барлық
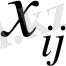 ішінен ең кішісі алынады
ішінен ең кішісі алынады
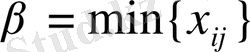
Жаңа жоспар келесідей құрылады:
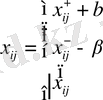
Содан соң жоспары бар торларға жаңа теңдеулер жүйесін жасамыз:
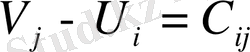
Ал жоспары жоқ торладың потенциалдығын зерттейиіз:
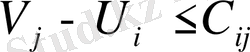 .
.
4 Оңтайландыру есебінің айқын математикалық өрнегінің өңделіп, жетілдіруі, оның сандық түрдегі шешімі
Z=2x 11 +4X 12 +X 13 +6X 14 +7X 15 +
+3X 21 +3X 22 +5X 23 +4X 24 +2X 25 +
+8X 31 +9X 32 +6X 33 +3X 34 +4X 35
X 11 +X 12 +X 13 +X 14 +X 15 =120
X 21 +X 22 +X 23 +X 24 +X 25 =110
X 31 +X 32 +X 33 +X 34 +X 35 =130
X 11 +X 21 +X 31 =80
X 12 +X 22 +X 32 =60
X 13 +X 23 +X 33 =70
X 14 +X 24 +X 34 =100
X 15 +X 25 +X 35 =50
Сипаттамалық кесте
Минималды элемент әдісі
B j
A i
30 0
80
0
60
0
70
20 0
100
0
50
50 0
120
2
50
4
0
1
70
6
0
7
0
80 20 0
110
3
30
3
60
5
0
4
20
2
0
80 0
130
8
8
9
0
6
0
3
80
4
50
80+60+70+100+50=360
120+110+130=360
∑A I =∑B J =80+60+70+100+50=120+110+130
Z MIN ЭЛЕМ =2*50+70*1+3*30+60*3+4*20+80*3+4*50=100+70+90+180+80+240+200=960
Солтүстік-батыс әдіспен жаңа жоспар
V j
U i
0 1
80
80 20
60
0 3
70
80 0
100
45 0
50
0
40
120
2
80
4
40
1
0
6
0
7 7
0
0
50 20 115
3
0
3
20
5
70
4
20
2
0
0 50
3 130
8
0
9
0
6
0
3
80
4
50
2*80+4*40+3*20+5*70+4*20+3*80+4*50=160+160+60+350+80+240+200=1250
uj-u i =c ig vj-u i <=cj g
v 1 -u 1 =2
u 1 =0 v 1 =2 v 3 -u 1 <=1 α 13 =5
v 2 -u 2 =4 u 1 =0 v 2 =4 v 4 -u 1 <=6
v 2 -u 2 =3 v 2 =4, u 2 =1 v 5 -u 1 <=7
v 3 -u 2 =5 v 3 =6 u 2 =1 v 1 -u 2 <=3
v 4 -u 2 =4 v 4 =5 u 2 =1 v 5 -u 2 <=2 α 25 =4
v 4 -u 3 =3 u 3 =2 v 4 =5 u 1 -u 3 <=8
v 5 -u 3 =4 v 5 =6 u 3 =2 v 2 -u 3 <=9
v 3 -u 3 <=6
Vj
U i
2
80
_ 4
40
+ 3
20
_ 5
70
4
20
3
80
4
50
J(-) min{40; 70}=40
V j
U i
2
80
1
40
3
60
5
30
_ 4
20
3
+ 80
4 4
_ 50
2*80+1*40+3*60+5*30+4*20+3*80+4*50=160+40+180+150+80+240+200=1050
v j -u i =c ii v j -u i <=c ij v 1 -u 5 <=8
v 1 -u 1 =c ij v 2 -u 1 <=4 v 2 -u 5 <=9
v 1 -u 1 =2 v 4 -u 1 <=6 v 3 -u 3 <=6
v 2 -u 2 =3 v 5 -u 1 <=7
v 3 -u 1 =1 v 1 -u 2 <=3
v 3- u 2 =5 v 5 -u 2 <=2
v 4 -u 2 =4
v 4 -u 3 =3
v 5 -u 3 =4
v 1 -u 1 =2 v 2 -u 1 <=4
u 1 =0, v 1 =2 v 4 -u 1 <=6
v 3 -u 1 =1 v 5 -u 7 <=7
u 1 =0, v 3 =1 v 2 -u 2 <=3
v 2 -u 2 =3 v 5 -u 2 <=2
v 2 =-1, u 2 =-4 v 1 -u 3 <=8
v 3 -u 1 =1 v 2 -u 3 <=9
v 3 =1, u 1 =0 v 3 -u 3 <=6
v-u2=5
v 2 =1, u 2 =4
v 4 -u 2 =4
v 2 =-4, v 4 =0
v 4 =0, u 3 =3
v 5 -u 3 =u
v 3 =-3, v 5 =1
u j -u i =c ij v j -u i <=c ij
v 1 -u 1 =2 v 2 -u 1 <=4
v 3 -u 1 =3 v 4 -u 1 <=6
v 2 -u 2 =3 v 5 -u 1 <=7
v 3 -u 1 =1 v 2 -u 2 <=3
v 3 -u 2 =5 v 5 -u 2 <=2
v 4 -u 2 =4 v 1 -u 3 <=8
v 4 -u 3 =3 v 2 -u 3 <=9
v 5 -u 3 =4 v 3 -u 3 <=6
V j
U i
_ 2
80
+ 1
40
3
60
5
_ 30
2
20
3
100
4
30
v j -u i =c ij v j -ui≤4
v 1 -u 1 =2 v 1 =2 v 2 -u 1 ≤4
v 3 -u 1 =1 v 3 =1 v 4 -u 1 ≤ 6
v 1 -u 2 =3 v 3 =-1 v 5 -u 1 ≤7
v 3 -u 2 =5 u 2 =-4 v 1 -u 2 ≤ 3 α 21 =3
v 5 -u 2 =2 v 5 =-2 v 4 -u 2 ≤4
v 4 -u 2 =3 v 4 =-3 v 1 -u 2 ≤8
v 5 -u 3 =4 u 3 =-6 v 2 -u 3 ≤9
v 3 -u 3 ≤6 α 33 =1
V ij
U i
V j -u i =c ij
V 1 -u 1 = 2 v 1 =2
V 3 -u 2 =1 v 3 =1
V 1 -u 2 =3 u 2 =-1
V 2 -u 2 =3 v 2 =2
V 5 -u 2 =2 v 5 =1 z*=100+70+90+180+40+300+120=900
V 4 -u 3 =3 v 4 =0
V 5 -u 3 =4 u 3 =-3
5 Программа листингісі
Program transportnaj_zadatsha;
Uses Crt;
Label l1;
Const N=6;
n1=7; n2=7;
Sa:longint=0;
Sb:longint=0;
Type predpr=Array [1. . N] of longint;
rasp=Array [1. . N, 1. . N] of longint;
Var A, B, alfa, betta, B_d, x:predpr;
c, p:rasp;
f, f0, x_min, Sp:longint;
Nt, x_p, r, r_min, ki, kj, Na, Nb, h, l, i, j:byte;
d:char;
u:Array[1. . N*N] of byte;
Procedure Nul (var a:predpr) ; {обнуляет массив}
var i:byte;
Begin
for i:=1 to N do a[i] :=0;
End;
Procedure PrintS (x, y:byte; s:string; c:byte) ;
Begin {вывод строки s}
TextColor(c) ;
GotoXY(x, y) ;
Write(s) ;
End;
Procedure Print (x, y:byte; n:byte; a:longint; c:byte) ;
Begin {вывод числа a}
TextColor(c) ;
GotoXY(x, y) ; Write(' ':n) ;
GotoXY(x, y) ; Write(a) ;
End;
Procedure Rid (var x:longint; y:byte) ; {проседура ввода числа x}
var i:integer;
s:string;
c:char;
j, k:byte;
Begin
s:=''; i:=1;
TextColor(11) ;
Repeat
c:=ReadKey;
Case ord(c) of
48. . 57: begin s:=s+c;
Write(c) ;
inc(i) ;
end;
8: if i>1 then begin dec(i) ;
Delete(s, i, 1) ;
Write(chr(8), ' ', chr(8) ) ;
end;
end;
j:=WhereX;
GotoXY(60, 1) ; ClrEOL;
if i>y then begin
TextColor(4) ;
Write('Не более ') ;
for k:=1 to y-1 do Write('9') ;
TextColor(11) ;
end;
GotoXY(j, 1) ;
Until (ord(c) =13) and (i<y+1) ;
val(s, x, i) ;
End;
Procedure goriz (a, b, c, d, e:char) ; {Процедуры goriz, wertic}
var i, j:byte; {и Tabl выводят таблицу}
Begin
Write(a) ;
for i:=1 to n2 do Write(b) ;
Write(c) ;
for i:=1 to Nb do begin
for j:=1 to n1 do Write(b) ;
if i<>Nb then Write(d) else Write(c) ;
end;
for i:=1 to 4 do Write(b) ;
Write(e) ;
End;
Procedure wertic;
var i:byte;
Begin
Write('¦', ' ':n2, '¦') ;
for i:=1 to Nb-1 do Write(' ':n1, '¦') ;
WriteLn(' ':n1, '¦', ' ' :4, '¦') ;
End;
Procedure Tabl;
Begin
ClrScr;
TextColor(1) ;
h:=6+Na*3;
l:=14+Nb*7;
GotoXY(1, 3) ;
for i:=3 to h do wertic;
GotoXY(1, 2) ;
goriz('+', '-', '-', '-', '+') ;
for i:=1 to Na+1 do begin
GotoXY(1, i*3+2) ;
if (i=1) or (i=Na+1)
then goriz('¦', '-', '+', '+', '¦')
else goriz('+', '-', '+', '+', '¦') ;
end;
GotoXY(1, h+1) ;
goriz('+', '-', '-', '-', '+') ;
TextColor(9) ;
for i:=1 to Na do begin
GotoXY(5, i*3+3) ;
Write('A', i) ;
end;
for i:=1 to Nb do begin
GotoXY(i*(n1+1) +n2-2, 3) ;
Write('B', i) ;
end;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz