Нүкте кинематикасы: қозғалыс теңдеулерінің берілу тәсілдері және жылдамдық пен үдеу


ЖОСПАР
КІРІСПЕ
Нүкте қозғалысы теңдеулерінің берілу тәсілдері
Нүкте жылдамдығы мен үдеуін анықтау
Нүкте қозғалысының теңдеуі табиғи тәсілмен берілген кездегі нүкте жылдамдығы мен үдеуін анықтау.
Нүктенің бірқалыпты және бірқалыпты айнымалы қозғалысы
ҚОРЫТЫНДЫ
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР
КІРІСПЕ
Бұл тарауда нүкте кинематикасы ғана мазмұндалады. Нүкте кинематикасында мынадай екі негізгі мәселе қарастырылады:
- Қозғалыстағы нүктенің берілген санақ жүйесіне қарағандағы орнын уақытқа тәуелді теңдеулер арқылы анықтау;
- осы теңдеулер арқылы қозғалыстағы нүктенің барлық кинематикалық сипаттамаларын (траекториясын, жылдамдығын, үдеуін) табу.
Таңдап алынған санақ жүйесіне қарағанда қозғалып бара жатқан нүктенің кеңістіктегі геометриялық орнындарын қосатын үздіксіз сызық нүкте траекториясы деп аталады.
Кез келген уақытта санақ жүйесіне қарағанда нүкте орнын анықтайтын теңдеулер белгілі болса, нүкте қозғалысы берілген деп есептеледі. Кинематикада нүкте қозғалысы үш түрде: векторлық, координаталық және табиғи тәсілдермен беріледі.
Нүкте қозғалысы теңдеулерінің берілу тәсілдері
Векторлық тәсіл. М нүктесі берілген санақ жүйесіне қарағанда қозғалады делік. Бұл нүктенің тұрақты О центріне қарағандағы орны, шамасы мен бағыты уақытқа тәуелді өзгеріп отыратын радиус-векторымен анықталады. Яғни радиус-вектор уақыттың (1-сурет) вектор-функциясы болады.
(1)
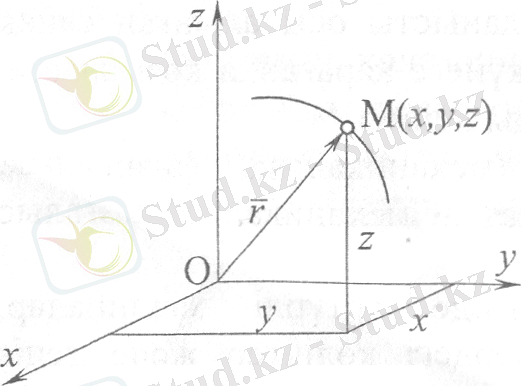
1-сурет
Мұнда - үздіксіз екі рет дифференциалданатын скалярлық аргуметтің функциясы.
Бүл теңдік нүкте қозғалысының векторлық теңдеуі деп аталады. Егер радиус-вектор тұрақты ( = const) болса, онда нүкте тыныштық қалпында болады. Осы теңдеу арқылы нүктенің негізгі кинематикалық сипаттамалары анықталады. Айнымалы радиус-векторы ұшының кеңістіктегі сызатын сызығы сол вектордың годографы деп аталады. Былайша айтқанда, қозғалыста болатын нүктенің траекториясы оның радиус-векторының годографы болады. Векторлық әдіс негізінен кинематика мен динамика тарауларында теориялық мәселелерді зерттеуде жиі қолданылады.
Координаталық тәсіл. Нүктенің кеңістіктегі орнын анықтау үшін тік бұрышты декарттық координаталар жүйесін (1-сурет) таңдап аламыз. Қозғалыс кезінде М нүктесінің х, у, z координаталары уақытқа тәуелді өзгеріп отырады, яғни
х = х(t), у = у(t), z =z (t) (2)
Бір мәнді, үздіксіз және кемінде екі рет дифференциалданатын x(t), y(t), z(t) функциялары М нүктесінің қозғалысын толық анықтайды. Осы (2) теңдеулерден әрбір уақыт кезеңіне сәйкес х, у, z мәндерін, яғни таңдап алынған Oxyz санақ жүйесіне қарағанда нүкте орнын анықтауға болады. Сондықтан (2) теңдеулерді нүктенің тік бұрышты декарттық координаталардағы қозғалыс теңдеулері деп немесе нүктенің қисық сызықты қозғалысының координаталық тәсілмен берілгендегі қозғалыс заңдары деуге болады.
Егер нүкте Оху жазықтықтығында қозғалатын болса, онда оның қозғалыс теңдеулері мына түрде жазылады:
х = x(t) ; у = y(t) . (3)
(2), (3) тендеулерінен (t) параметрін шығарып тастап, нүкте траекториясьгның теңдеуін жазуға болады.
Егер нүкте түзу сызықты қозғалатын болса, онда оның траектория бойындағы қозғалыс теңдеуі
x = x (t) . (4)
Радиус-вектордың координаталар өстеріндегі проекцияларын r х =х, r х =у, r z =z деп алсақ, векторлық және координаталық тәсілдердің қозғалыс теңдеулері арасындағы байланысты бағыттары тұрақты , , (i=j=k=l ) бірлік векторлары арқылы жазуға болады, яғни
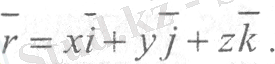 (5)
(5)
Мысал:
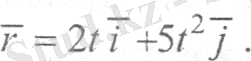 Бұл мысалда
x = 2t, y=5t,
2 = 0 және нүкте
Оху
жазықтықтығында қозғалатынын білуге болады.
Бұл мысалда
x = 2t, y=5t,
2 = 0 және нүкте
Оху
жазықтықтығында қозғалатынын білуге болады.
Қозғалыс теңдеуі векторлық тәсілмен берілсе, нүкте қозғалысын үш скалярлық теңдеудің орнына бір теңдеумен жазуға болады. Векторлық тәсіл кинематика мен динамика теоремаларын дәлелдеуге кеңінен қолданылады.
Нүкте траекториясын анықтау. (2) және (3) теңдеулер нүкте траекториясының параметрлік теңдеулері болады. Осы теңдеулерден уақытты жойсақ, нүкте траекториясының координаталар түріндегі теңдеуін, яғни нүктенің координаталары арасындағы тәуелділікті аламыз.
М нүктесінің траекториясын графикалық жолмен де табуға болады. Ол үшін берілген (2) және (3) қозғалыс теңдеулеріне уақыттың мәндерін қоя отырып нүктенің таңдап алынған санақ жүйесіне қарағандағы орындарын анықтап оларды жатық қисықпен қосамыз.
Механизм конструкциясының ерекшеліктеріне байланысты көптеген есептерде нүкте қозғалысы геометриялық шарттармен анықталады. Осы шарттар арқылы қажетті нүктенің қозғалыс тендеуі мен траекториясы анықталады.
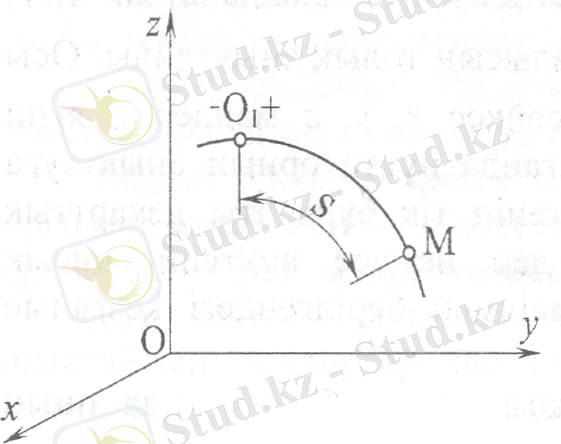
2-сурет
Табиғи тәсіл. Қозғалыс бұл тәсілмен берілгенде (2-сурет) нүкте -траекториясы мен оның осы траектория бойындағы қозғалысының теңдеуі белгілі болады. Траекториядағы О 1 М =s қашықтығын есептеудің бастапқы нүктесін белгілеп, оң және теріс бағыттарын келісіп алған жөн; траектория бойымен өлшенетін, сәйкес таңбамен алынған О 1 нүктесінен М нүктесіне дейінгі қашықтыққа тең кисық сызықты доғалық координатасы, М нүктесінін траекториясындағы, сонымен бірге Oxyz санақ жүйесіндегі орнын анықтайды. Бұдан бұрын уақыттың бастапқы кезін (t=0) анықтап, белгілеп алу қажет. Егер әрбір t уақыт кезіндегі М нүктесінің траекториядағы орнын анықтайтын s(t) заңдылылығы белгілі болса, онда нүкте қозғалысы берілген деп саналады, яғни
s=s(t) . (6)
(6) теңдеуі нүкте қозғалысының табиғи тәсілмен берілгендегі қозғалыс заңы деп аталады.
Сонымен, нүкте қозғалысы табиғи тәсілмен берілгенде мыналар белгіленуі қажет: 1) нүкте траекториясы; 2) траектория бойында s қашықтығы есептелінетін бас нүктенің орны мен оның оң және теріс бағыттары және уақыттың бастапқы кезі; 3) нүктенің траектория бойындағы қозғалыс заңы s=s(t) .
Қозғалыс табиғатына сай s=s(t) функциясы бір мәнді, үздіксіз және екі рет дифференциалданатын болуы қажет.
Координаталық және табиғи тәсілдермен берілген нүкте қозғалысының арасындағы байланыс. Егер нүкте қозғалысы координаталық тәсілмен берілген болса, онда табиғи тәсілге көшу үшін мыналарды анықтап алу қажет: 1) нүкте траекториясының теңдеуі; 2) нүктенің бастапқы уақыт кезеңіндегі орны; 3) нүктенің траектория бойындағы қозғалыс заңы. Нүктенің қозғалыс теңдеуі координаталық тәсілмен берілген кезде, оның траекториясының теңдеуі қалай анықталатыны бізге белгілі. Қозғалушы нүктснің бастапқы уақыт кезеңіндегі орнын анықтау үшін (2) тендеулеріне t =0 мәнін қою керек. Енді осы (2) теңдеулер арқылы нүктенің траектория бойындағы қозғалыс теңдеуін анықтайық.
Дифференциалдық геометриядан траектория доғасының элементі немесе нүктенің қисық сызықты координатасының дифференциалы
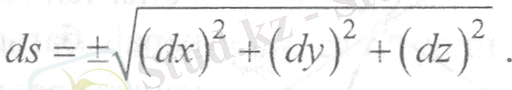
Мұнда таңбасы нүкте доғалық координатаның оң бағытында (яғни s функциясы өсіп отырады) қозғалыста болатынын көрсетеді.
Осы тендеудің сол жағын s 0 ден s-ке және оң жағын нөлден t - ға дейінгі шектерде интегралдай отырып, нүктенің траектория бойындағы қозғалысының теңдеуін анықтаймыз.
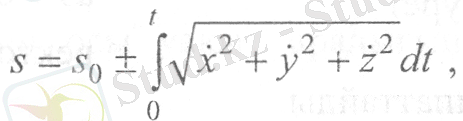 (7)
(7)
мұндагы
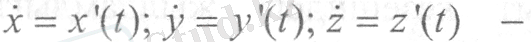 қозғалушы нүктенің координаталарынан уақыт бойынша алынған бірінші туындылар.
қозғалушы нүктенің координаталарынан уақыт бойынша алынған бірінші туындылар.
Егер нүкте түзу сызықты қозғалса, онда нүктенің координаталық тәсілмен берілген қозғалысы, табиғи тәсілге келтіріледі.
Нүкте жылдамдығы мен үдеуін анықтау
Нукте жылдамдығы мен үдеуі-нүкте қозғалысының негізгі кинематикалық сипаттамалары болып табылады.
Нүкте қозғалысының теңдеуі векторлық тәсілмен берілген кездегі нүкте жылдамдығы мен үдеуін анықтау.
Жылдамдық нүктенің бірлік уақытта орын ауыстыру тездігін (шапшаңдығын) анықтайтын физикалық шама. Жылдамдықтың өлшем бірлігі ретшде халықаралық СИ жүйесінде м/сек алынады.
Енді жылдамдықтың қалай анықталатынын қарастырайық. М нүктесі қисық сызықты траекторияның бойымен қозғалатын болсын. Нүктенің кез келген t уақыт кезеңіндегі М орны радиус-векторымен, ал келесі t 1 =t + ∆t уақыт кезеңіндегі М орны = радиус-векторымен (3-сурет) анықталады делік.
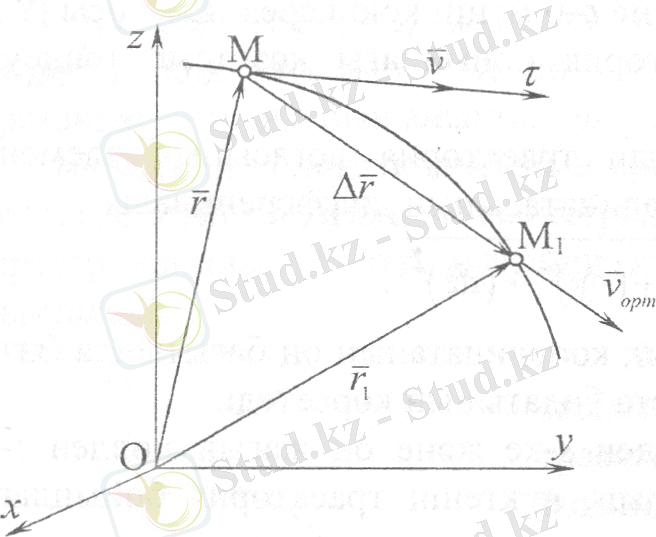
3-сурет
Сонда М нүктесінің ∆t = t 1 - t уақыт аралығындағы орналастырылуы радиус-векторымен анықталады. Осы векторының сәйкес ∆ t уақыт өсімшесіне қатынасы, яғни
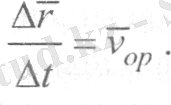 (8)
(8)
М нүктесінің ∆t уақыт аралығындағы орташа жылдамдығы деп аталады және оның векторы ММ 1 қиюшысының бойымен қозғалыстың бағытына қарай бағытталады. Нүктенің ∆t уақыт аралығындағы орташа жылдамдық векторының шамасы мен бағыты осы уақыт аралығына тәуелді екенін атап кетуге болады. Осы ∆t уақыт аралығы неғұрлым аз болса, орташа жылдамдық векторы векторының өзгеруін соғұрлым дәлірек сипаттайды.
Нүктенің кез-келен уақыт кезеңіндегі жылдамдығы орташа жылдамдықтың ∆ t уақыт аралығы нөлге ұмтылғандағы шегі ретінде анықталады, яғни
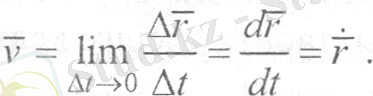 (9)
(9)
Сонымен, нүкте қозғалысы векторлық тәсілмен берілгенде, оның жылдамдыгы радиус-вектордан уақыт бойынша алынган бірінші туындыға тең ввкторлық шама болады. Бұл жылдамдық нүктенің лездік жылдамдығы болып табылады. Уақыт аралығы ∆t нөлге шексіз ұмтылғанда, MM 1 түзуі жанамаға ұмтылатындықтан, М нүктесінің лездік жылдамдығының векторы траекторияның сол нүктесі арқылы жүргізілген Мτ жанамасының бойымен қозғалыстың бағытына қарай бағытталады.
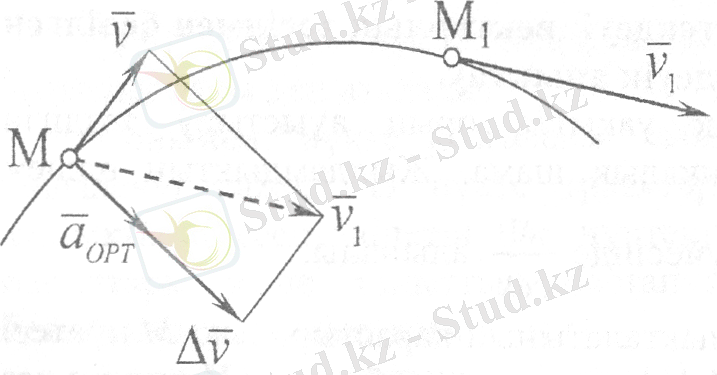
4-сурет
Жалпы жағдайда нүктенің қисық сызықты қозғалысында жылдамдық векторының шамасы мен бағыты өзгеріп отырады. Нүкте түзу сызықты қозғалғанда жылдамдық векторы әрдайым нүкте қозғалып бара жатқан түзудің бойымен бағытталады, сондықтан тек қана жылдамдықтың шамасы ғана өзгереді.
Жылдамдық векторының бірлік уақыттағы шамасы мен бағытының өзгеру шапшаңдығы үдеу деп аталады. Үдеудің өлшем бірлігі ретінде халықаралық СИ жүйесінде алынады.
М нүктесінің t уақыт кезеңіндегі жылдамдығын деп белгілеп (4-сурет), ал ∆t = t 1 − t уақыт аралығы өткен соң жылдамдығы болсын делік. Онда жылдамдықтың осы уақыт аралығындағы өсімшесі ∆ = - векторымен анықталады. ∆ векторын салу үшін М нүктесіне - ге тең вектор түсіріп диагоналы , ал бір қабырғасы болатын параллелограмм тұрғызамыз. Параллелограммның екінші қабырғасы ∆ векторын бейнелейді және ол вектор әр уақытта траекторияның қарастырылып отырған аумағының ойыс жағына қарай бағытталатынын байқаймыз. Жылдамдық векторының ∆ өсімшесінің сәйкес ∆t уақыт аралығына қатынасы нүктенің осы уақыт аралығындағы орташа үдеу векторын анықтайды:
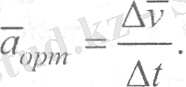 (10)
(10)
векторының бағыты жылдамдық өсімшесі ∆ векторының бағытымсн бағыттас және траекторияның қарастырылып отырған аумағының ойыс жағына қарай бағытталған, бірақ түсірілстін нақты нүктесінің орны болмайды.
Нүктенің берілген t уақыт кезеңіндегі үдеуі, орташа үдеудің ∆t уақыт аралығы нөлге ұмтылғандағы шегі ретінде анықталады, яғни
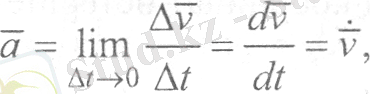 (11)
(11)
немесе
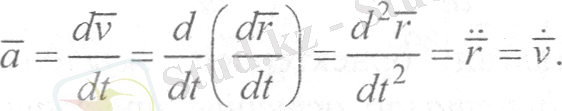 (12)
(12)
Сонымен, нүкте қозғалысы векторлық тәсілмен берілгенде, оның үдеуі жылдамдық векторынан уақыт бойынша алынған бірінші немесе нүктенің радиус-векторынан уақыт бойынша алынған екінші туындыға тең векторлық шама болады.
Сонымен берілген уақыт кезеңінде нүкте үдеуінің векторы жанасушы жазықтықта жатады және кисықтың ойыс жағына қарай бағытталады.
Нүкте қозғалысының теңдеуі координаталық тәсілмен берілген кездегі нүкте жылдамдығы мен үдеуін анықтау. Кеңістікте емін еркін қозғалып бара жатқан нүктенің қозғалысын Oxyz координаталар жүйесіне (5-сурет) қатысты қарастырайық. Жылдамдық векторы нүктенің радиус-векторынан уақыт бойынша алынған бірінші туындыға тең екенін ескере отырып (5) теңдігінің екі жағынан да уақыт бойынша туынды аламыз.
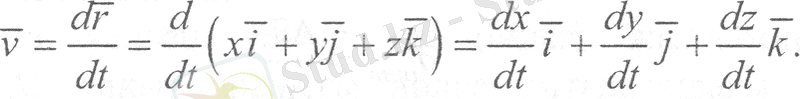 (13)
(13)
4-суретте нүкте жылдамдығының векторы Oxyz координат өстері бойымен құраушыларға жіктелуі көрсетілген, яғни
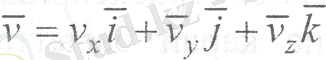 (14)
(14)
мұнда: v x , v у , v z - жылдамдық векторының O x , O y , O z өстеріне проекциялары (13) және (14) формулаларының оң жақтарының теңдігінен, нүкте жылдамдығының координат өстеріне проекцияларын мынадай түрде жазуға болады:
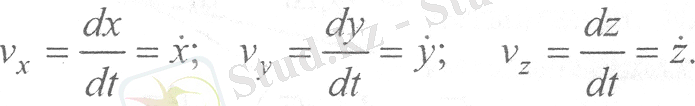
(15)
Осы анықталған өрнектерден жылдамдықтың тік бұрышты декарттық координаталар өстеріне проекциялары қозғалушы нүктенің сәйкес координаталарынан уақыт бойынша алынған бірінші туындыларына тең болатынын көреміз.
Жылдамдықтың сан мәнін (модулін) оның проекциялары арқылы анықтаймыз
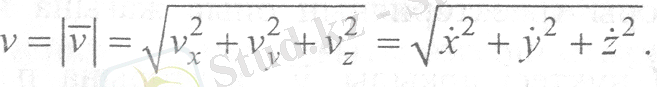 (16)
(16)
Жылдамдық векторының бағыты бағыттаушы косинустар арқылы анықталады.
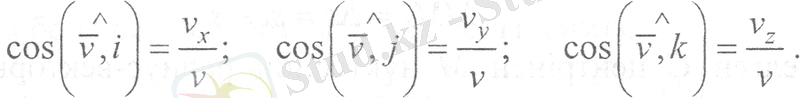 (17)
(17)
Үдеуді анықтау үшін (9) және (14) теңдеулерінің екі жағынан да уақыт ойынша туынды алайық:
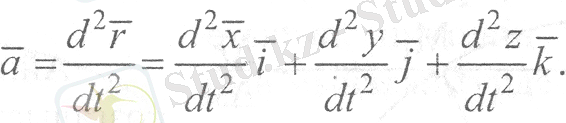 (18)
(18)
Немесе
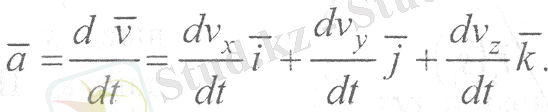 (19)
(19)
Үдеу векторын координат өстеріне мынадай түрде жіктеп жазуға болады:
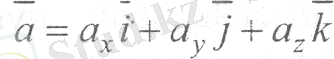 (20)
(20)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz