Созылу немесе сығылу

Күш әсеріне дейін білеудің бетіне оның өсіне перпендикуляр түзу сызықтар жүргіземіз (19.3-сурет). Әрбір сызықты білеудің көлденең қимасының ізі ретінде қарастыруға болады. Білеуді өстік F күшімен жүктегенде бұл сызықтар түзу бір-біріне параллель күйінде қалады, олар штрих сызықтармен көрсетілген. Осының негізінде күштің әсеріне дейінгі жазық қималар, күштің әсерінен кейін де жазық күйін сақтайды. Бұл тәжірибе жазық қималар туралы Бернулли гипотезасын растайды. Білеуді шексіз талшықтардан тұрады деп есептейік. Кез келген өзара параллель екі көлденең қима, созылғанда өзара параллель күйін сақтайды, бірақ бір бірінен белгілі шамаға алшақтайды, әрбір талшық осы шамаға тең ұзарады. Талшықтардың ұзаруына бірдей кернеулер сәйкес келеді, сондықтан әрбір көлденең қимадағы кернеулердің өзгеру заңдылығы тұрақты. Осыған байланысты (19.1) өрнегіндегі тік кернеуді интеграл алдына шығаруға болады.

ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР:

1. А.Іңкәрбеков, С.Жүнісбеков, Ә.Қадырбаев, Ж.Жұмағұлов «Техникалық механика», Алматы: 2009 ж.
2. М.Д. Шинибаев «Теориялық механика» Алматы: 2009
3. А.Дасибеков, М.М. Мирсаидов «Теориялық механика (Кинематика)».Алматы: 2010
4. А Дасибеков, М.М. Мирсаидов «Теориялық механика (Статика)». Алматы: 2010.
5. Дүрманов Б. Жәнібеков Ж. Тобжанова Б. «Жылу техникалары мен жабдықтарын жөндеу және пайдалану» Астана: 2011
6. Ақылбаев Ж. Гладков В. Ильина Л. Тұрмұхамбетов А. «Механика» Астана: 2011
7. Дасибеков А., Мирсаидов М.М. Теориялық механика (Кинематика). «Кітап», Ш., 2010.
8. Дасибеков А., Мирсаидов М.М. Теориялық механика (Статика). «Кітап», Ш., 2010.

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 62 бет
Таңдаулыға:

Жоспар

Кіріспе
Бойлық күш
Білеудің көлденең және көлбеу қималарындағы кернеулер
Бойлық және көлденең деформациялар
Созу және сығу диаграммалары
Статикалық күштің жұмысы. Деформацияның потенциалдық энергиясы
Мүмкіндік кернеулер. Беріктікке есептеу
Статикалық анықталмаған жүйелер
Температуралық кернеу
Пайдаланылған әдебиеттер

Кіріспе

Күш әсеріне дейін білеудің бетіне оның өсіне перпендикуляр түзу сызықтар жүргіземіз (19.3-сурет). Әрбір сызықты білеудің көлденең қимасының ізі ретінде қарастыруға болады. Білеуді өстік F күшімен жүктегенде бұл сызықтар түзу бір-біріне параллель күйінде қалады, олар штрих сызықтармен көрсетілген. Осының негізінде күштің әсеріне дейінгі жазық қималар, күштің әсерінен кейін де жазық күйін сақтайды. Бұл тәжірибе жазық қималар туралы Бернулли гипотезасын растайды. Білеуді шексіз талшықтардан тұрады деп есептейік. Кез келген өзара параллель екі көлденең қима, созылғанда өзара параллель күйін сақтайды, бірақ бір бірінен белгілі шамаға алшақтайды, әрбір талшық осы шамаға тең ұзарады. Талшықтардың ұзаруына бірдей кернеулер сәйкес келеді, сондықтан әрбір көлденең қимадағы кернеулердің өзгеру заңдылығы тұрақты. Осыған байланысты (19.1) өрнегіндегі тік кернеуді интеграл алдына шығаруға болады.

СОЗЫЛУ НЕМЕСЕ СЫҒЫЛУ
Бойлық күш

Сыртқы күштің әсерінен білеудің көлденең қималарында тек бойлық күш N пайда болатын деформацияның түрі орталық созылу немесе сығылу деп аталады. Қалған ішкі күштер (көлденең күш, ию моменті, бұралу моменті) нөлге тең.

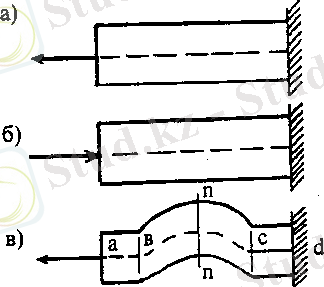
19.1-сурет.

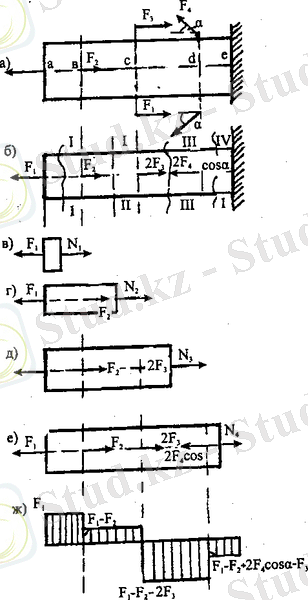
19.2-сурет

Созылу сығылу деформациясына жұмыс істейтін білеу сырық деп аталады. 19.1,а-суретте бір ұшы қатаң бекітілген, екінші ұшында өсі бойымен жүктің әсерімен бейнеленген тік білеу көрсетілген. Бұл білеудің барлық көлденең қимасында тек созушы бойлық күш пайда болады, сондықтан білеу орталық созылған. Күштің кері бағытында (19.1,б-сурет) білеу орталық сығылған.
19.1,в-суреттегі білеудің ab мен cd аралығы орталық созылады, ал bc аралығындағы кез-келген п-п қимасында бойлық күшпен қатар көлденең күш және ию моменті пайда болады.
Созушы бойлық күш оң таңбалы, ал сығушы бойлық күш теріс таңбалы деп есептелінеді.
19.2,а-суретте көрсетілген сырыққа өсі бойымен F1, F2 күштері, өсінен бірдей қашықтықта жатқан оған параллель екі F3 және өспен α бұрышын жасайтын екі F4 күштері әсер етеді.
Күштерді өсі бойына жинаған суретте сырықтың есептеу нұсқасы көрсетілген, сондықтан сырықтың кез келген көлденең қимасында тек бойлық күш пайда болады. Бойлық күштерді қию әдісімен анықтайды. Сырық қанша аралыққа бөлінсе, сонша рет қию әдісін пайдаланады. Қию әдісін сырықтың бос ұшынан бастап, қолданған ыңғайлы, себебі қатаң бекітпедегі тірек реакциясы белгісіз.
Бірінші аралық ab кез келген жерінен І-І қимасы арқылы екіге бөлінеді (19.2,в-сурет).
Қиманың оң бөлігінің сол бөлікке әсерін N1 арқылы белгілеп, оның оң таңбалы (созушы) деп есепеп, содан оңға қарай бағыттайды. Есептеу нәтижесінде N1 таңбасы теріс болса, онда сырық бұл аралықа сығылады.
19.2,в-суреттегі қиылған бөліктің тепе-теңдігін қарастыратын болса, барлық күштерді сырық өсіне проекциялайды, яғни
Σx=N1-F1=0 немесе N1-F1
N2 анықтау үшін bc аралығының кез келген жерінен сырықта II-II қимасымен екіге бөледі. Тепе-теңдік теңдеуінен (19.2, г-сурет)

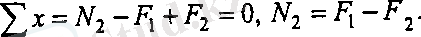
Дәл осындай қалған cd, de арқылы аралықтардағы бойлық күштер (19.2,д-сурет)

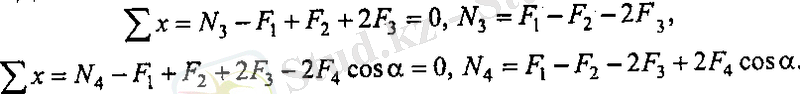
Есептеулердің негізінде әрбір аралықтағы бойлық күштер тұрақты болатындығына көз жеткізуге болады.
Бойлық күштің сырық боймен өзгеру графигі, бойлық күштің эпюрасы деп аталады. Эпюраны тұрғызу үшін, сырық өсіне параллель эпюра өсін жүргізеді (19.2,ж-сурет). Белгілі бір масштабпен осы өске перпендикуляр бағытта әрбір аралық үшін бойлық күштің мәні тұрғызылады. Тұрғызылған эпюраны өске перпендикуляр түзумен штрихтайды (19.2,ж-сурет). Әрбір штрих сызықтың сәйкес көлденең қималарындағы бойлық күштің мәнін білдіреді. Күш әсері бар қималарда, бойлық күш эпюрасында күшке тең секірістер пайда болады, осыған байланысты a, b, c, d, e нүктелерінде секірістер сәйкесінше F1, F2,- 2F3, - 2F4cosα тең.
Ішкі күштердің эпюрасын тұрғызғанда сырықты және есептеу нұсқасын көрсету міндетті емес, екеуінің біреуі көрсетілсе жеткілікті. Сонымен қатар, сырықтың жеке бөліктерін де көрсету аса қажет емес.
Жоғарыдағы сырықты есептегенде, тек сырықтағы (19.2,а-сурет) немесе есептеу нұсқасын (19.2,б-сурет) және бойлық күштің эпюрасын (19.2,ж-сурет) көрсетсе жеткілікті.

Білеудің көлденең және көлбеу қималарындағы кернеулер

Білеудің көлденең қимасында бір қалыпты таралған тік күштердің (кернеулердің) қорытқы күші бойлық N күші болап табылады. Ол тік кернеумен келесі түрде байланысқан.

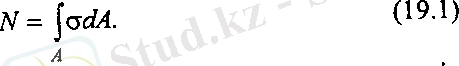
Мұндағы σ қарапайын ауданшадағы кез келген нүктеде әсер ететін тік кернеу, А білеудің көлденең қимасының ауданы.
Σ dA=dN, dA ауданшадағы қарапайым бойлық күш. Кернеудің әрбір нүктедегі мәнін анықтау үшін оның қимадағы өзгеру заңдылығын білу қажет. Бұл заңдылық тәжірибе жүзінде анықталады.
Күш әсеріне дейін білеудің бетіне оның өсіне перпендикуляр түзу сызықтар жүргіземіз (19.3-сурет). Әрбір сызықты білеудің көлденең қимасының ізі ретінде қарастыруға болады. Білеуді өстік F күшімен жүктегенде бұл сызықтар түзу бір-біріне параллель күйінде қалады, олар штрих сызықтармен көрсетілген. Осының негізінде күштің әсеріне дейінгі жазық қималар, күштің әсерінен кейін де жазық күйін сақтайды. Бұл тәжірибе жазық қималар туралы Бернулли гипотезасын растайды. Білеуді шексіз талшықтардан тұрады деп есептейік. Кез келген өзара параллель екі көлденең қима, созылғанда өзара параллель күйін сақтайды, бірақ бір бірінен белгілі шамаға алшақтайды, әрбір талшық осы шамаға тең ұзарады. Талшықтардың ұзаруына бірдей кернеулер сәйкес келеді, сондықтан әрбір көлденең қимадағы кернеулердің өзгеру заңдылығы тұрақты. Осыған байланысты (19.1) өрнегіндегі тік кернеуді интеграл алдына шығаруға болады.

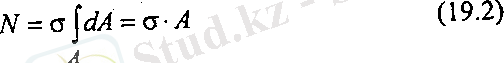
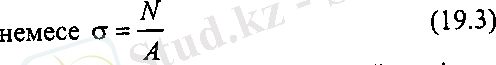
19.3-сурет

Сонымен, білеуді орталық созғанда немесе сыққанда оның көлденең қимасында бойлық күштің көлденең қима ауданының қатынасына тең тұрақты тік кернеу пайда болады.
Білеу қимасы әлсізденгенде (тесікер арқылы), кернеуді есептегенде көлденең қима ауданының әлсіздігін ескеру керек, яғни (19.3) формуладағы А-ның орнына Анетто қолданылады.
Тік кернеудің өзгеру заңдылығын білу үшін оның эпюрасы тұрғызылады. Бұл эпюраның өсі сырық өсіне параллель. Сырық қимасы тұрақты болғанда, тік кернеу эпюрасының түрі, бойлық күш эпюрасының түріне ұқсас, ал қимасы айнымалы сырық үшін тік кернеу эпюрасында тек күш әсері бар қимада ғана емес, қима өзгеретін жерде де секіріс болады.
Көлбеу қималардағы кернеулерді анықтауға тоқталсақ.

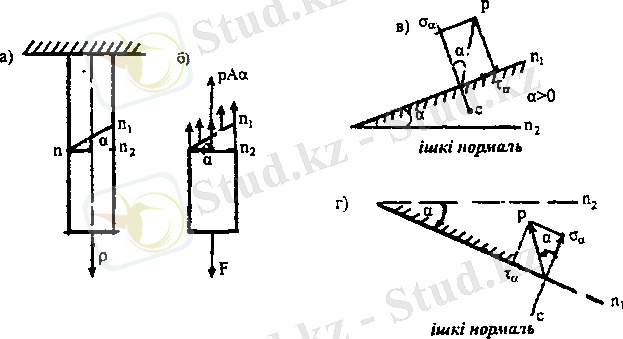
19.4-сурет

Көлбеу қима n-n1 мен көлденең қима n-n2 арасындағы бұрышты α арқылы белгілейміз. Көлденең қиманы сағат тіліне қарсы бұрғанда, көлбеу, қимамен сәйкес келсе, α бұрышы оң, кері жағдайда теріс таңбалы деп есептейміз.
Созылу немесе сығылу деформациясында сырық өсіне параллель талшықтардың ұзаруы бірдей болғандықтан, көлбеу қиманың барлық нүктесіндегі толық кернеу бірдей.
n-n1 қимасы арқылы сырықтан қиып алынған төменгі бөліктің тепе теңдігінен (19.4,б-сурет).

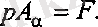
Мұндағы Аа көлбеу қиманың ауданы. А=Ааcosα ескерсек

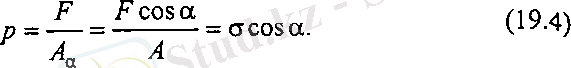
Толық кернеуді тік тік σα және жанама τα кернеулерге жіктесек

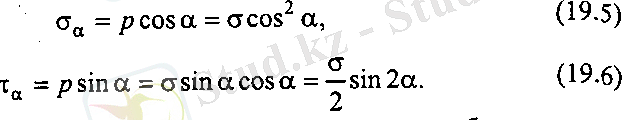
Созылғанда тік кернеу оң таңбалы, сығылғанда теріс таңбалы.
Ішкі нормалардың бойында жатқан С нүктесіне қатысты жанама кернеудің векторы, денені сағат тіліне бағыттас бұраса, ол оң таңбалы (19.4,в-сурет), кері жағдайда теріс таңбалы (19.4,г-сурет).
(19.5) формуладағы тік кернеудің мәні 0 деп (α=90°), FA (α=0) дейін өзгереді. Ең үлкен тік кернеу көлденең қимада пайда болады, сондықтан сығылған немесе созылған сырықты көлденең қимадағы тік кернеу арқылы беріктікке есептейді.
(19.6) формуладан жанама кернеу σ2=F(2A)-дан (α=45°), σ2=F(2A)-ға (α=-45°) дейін өзгереді. α=0, α=90°-та τ=0, яғни тік кернеудік ең үлкен немесе ең кіші мәнге ие болатын қималарында жанама кернеу нөлге тең. Өзара перпендикуляр қималардағы жанама кернеулерді анықтайық. (α2=α1-90°)

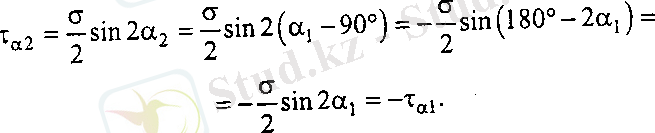
Сонымен, өзара перпендикуляр қималардағы жанама кернеулер өзара тең, таңбалары қарама-қарсы.

Бойлық және көлденең деформациялар

Ұзындығы l, бір ұшы қатаң бекітілген, екінші ұшында F күшімен тартылған, қимасы тұрақты білеуді қарастырайық (19.5,а-сурет). F күшінің әсерінен білеу толық немесе абсолюттік Δl шамаға ұзарады. Білеудің кез келген нүктесіндегі кернеулі күй бірдей, сондықтан εx сызықтық деформациясы барлық нүктеде бірдей. Осыған орай εx=Δll салыстырмалы ұзару немесе салыстырмалы ұзару немесе салыстырмалы бойлық деформация деп аталады.

19.5-сурет

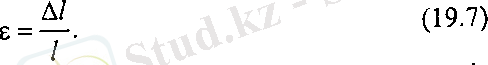
Ұзару деформациясы оң (19.6,а-сурет), сығылу деформациясы теріс (19.5,б-сурет). Созушы күш неғұрлым көп болса, соғұрлым білеудің ұзаруы көп болса, соғұрлым білеудің ұзаруы көп, керісінше, неғұрлым білеудің көлденең қимасының ауданы көп болса, соғұрлым білеудің ұзаруы аз. Білеудің ұзаруы (қысқаруы), оның материалына тәуелді. Білеу бойындағы кернеу пропорционалдық шектен аспаған жағдайда, тәжірибе жүзінде келесі тәуелділік табылған.

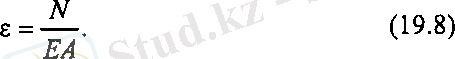
Мұндағы N - бойлық күш, А көлденең қиманың ауданы, Е - материалдың физикалық қасиетіне байланысты анықталатын коэффициент.
(19.3) формуласын ескеретін болсақ

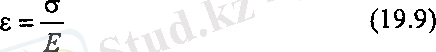
немесе

Білеудің абсолюттік ұзаруы

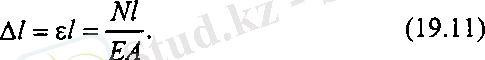
Деформация мен күш бір бірімен тура пропорционалдық байланыста болатындығын, алғашқы болып Р.Гук (1660 ж) тұжырымдаған. (19.8) - (19.11) созылу немесе сығылудағы Гук заңының математикалық өрнектері болып табылады.
Гуктің негізгі заңы (19.9), (19.10). Салыстырмалы бойлық деформация тік кернеуге тура пропорционал.
Жоғарыдағы формулалардағы Е бірінші текті серпімділік модулі (серпімділік модуль) деп аталады.
Ол қатаңдықты білдіретін материалдың физикалық тұрақтысы.
ЕА - созылған немесе созылған білеудің көлденең қимасының қатаңдығы.
(19.11) формуласы білеудің ұзындығы l аралықта тек көлденең қимасы тұрақты жағдайда қолданылады.
Білеу созылғанда немесе сығылғанда бойлық деформациясымен қатар көлденең деформация да орын алады.
Білеу сығылғанда, оның көлденең қимасы ұлғаяды. Күш әсеріне дейін көлденең білеудің көлденең өлшемі b болса, күш әсерінен кейін, ол b+Δb. Δb - абсолюттік көлденең деформация.
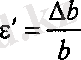- салыстырмалы көлденең деформация. (19.6-сурет)

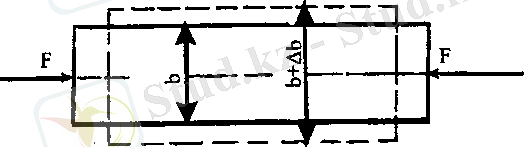
19.6-сурет

Кернеу серпімділік шегінен аспағанда тәжірибенің негізінде көлденең деформация бойлық деформацияға тура пропорционал болатындығы көрсетілген.

μ - білей материалына байланысты көлденең деформация коэффициенті немесе Пуассон коэффициенті деп аталады.
Пуассон коэффициенті μ мен серпімділік модулі Е материалдың серпімділік қасиетін білдіреді.
Созу және сығу диаграммалары

Зерттейтін материалдан жасалған арнайы үлгіні сынау негізінде, оның механикалық сипаттамалары анықталады. статикалық соз.ылуға зерттеу кеңінен таралған. Кейбір тас, беторн, цемент, т.с.с. құрылыс материалдары сығуға зерттеледі.
Зерттеу арнайы машиналарда жүргізіледі. Сынақ барысында арнайы қондырғы үлгіге әсер етуші бойлық күш пен оның ұзаруын байланыстыратын график сызылады, яғни күш пен координата жүйесінде диаграмма алынады. Материалдың қасиеттерін тереңірек түсіну үшін кернеу мен салыстырмалы деформация координата жүйесіндегі диаграмма қолайлы. 19.7-суретте азкөміртекті болаттың созылу диаграммасы көрсетілген.

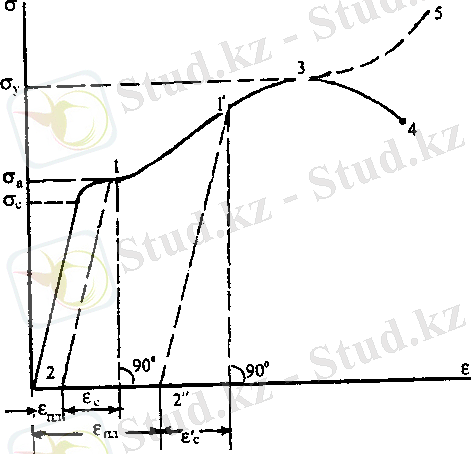
19.7-сурет
Созушы кернеу серпімділік шегі деп аталатын σс мәніне жеткенше, диаграмма түзу сызық, яғни салыстырмалы ұзару кернеуге тура пропорционал, басқаша айтқанда бұл арада Гук заңы орындалады.
Серпімділік шегіне жеткеннен соң ε кернеуге тура пропорционал емес жылдамырақ өзгереді. Кернеу σа аққыштық шегі деп аталатын мәніне жеткен соң, кернеу өспесе де деформация өсуін тоқтатпайды, диаграммада абцисса өсіне параллель аралық пайда болады. Бұл құбылыс материалдың аққыштығы.
Диаграмманың абцисса өсіне параллель аралық, аққыштық аймақша деп аталады. бұл аймақшада жылтыратып өңделген болат үлгінің беті күңгірттеніп, оның өсіне 45° бұрыш жасайтын сызықтар пайда болады. Бұл сызықтарды алғашқы орыстың атақты металлургі Д.К.Чернов байқаған (1839-1921). Сондықтан айтылған сызықтар Чернов сызықтары деген атқа ие болған (19.8-сурет).

19.8-сурет
Металлографиканың зерттеулерінің негізінде аққыштық болат кристалдарының ығысуымен түсіндіріледі, ал Чернов сызықтары осының салдарынан пайда болады.
Үлгінің созылуын жалғастырғанда кернеу ұлғая түседі. Диаграмманың аққыштық аймағының соңынан ең биік нүктеге дейінгі 1-3 аралық қатаю аралығы, үлгі қирамай шыдайтын ең үлкен шартты кернеу беріктік шегі немесе уақытша кернеу σу деп аталады. үлгінің ары қарай созылуы созушы күштің кемуіне әкеледі. Беріктік шек σу ең үлкен созушы күшті үлгінің алғашқы көлденең қимасының ауданына бөлгенге тең.

19.9-сурет
Қатаю аралығында күшті өсіргенде, үлгіде жергілікті жіңішкеру - қылта мойын пайда болады (19.9-сурет). Бұл құбылыс кезінде шартты кернеу күшті, алғашқы қима ауданына бөлгенге тең, сондықтан күштің төмендеуіне сәйкес кернеу де кемиді. (19.7-сурет 3-4 аралық). Қылта мойын қимасындағы нақты кернеу 19.7-суреттегі 3-5 аралықтағыдай өсуі тиіс.
Нақты кернеу мен шартты кернеудің айырмашылығы беріктік шекке жеткенде ғана емес, сынақтың барысында да болады, себебі көлденең деформация негізінде үлгінің қимасы кішірейеді, бірақ күштің уақытша кернеуге жеткенше айтылған айырмашылығы өте аз.
Сыналатын үлгі серпімділік шегіне дейін жүктеп, жүктен босатса, үлгінің деформациясы жүктелгенде қандай заңдылықпен өссе, сол заңдылықпен кемиді, яғни үлгіде тек серпімді деформация пайда болады.
Көптеген материалдар үшін серпімділік шек пен пропорционалдық шек сәйкес келеді.
Үлгі серпімділік, шектен жоғарыда жүктен босатылса, деформация толық жойылмайды, диаграммада ол 1-2 немесе 1′-2′ түзулерімен көрсетілген. Бұл жағдайда үлгінің толық деформациясы серпімділік εс (ε′с) және пластикалық εпл (ε′пл) деформациялардан құралады. Жүктен босатылған үлгіні қайта жүктелгенде, диаграмма әуелі 2 - 1 (2′ - 1′) түзуімен одан ары 1-3-4 (1′-3′-4′) қисығымен бейнеленеді.
Сонымен, үлгіні қайта жүктегенде, оның пропорционалдық шегі, шектен босатылған нүктеге дейін өседі. Бұл құбылыс, техникада кеңінен қолданылатын шынығу деген атқа ие. Мысалы, электр желісіндегі сымдардың салбырауын болдырмас үшін, әуелі оны тартып шынықтырады. Шынығу қажетсіз жағдайда (себебі, материалдың морттық қасиеті жоғарылайды) материалды қыздырып, оны төмендетеді.
Үлгіні созып үзгеннен соң, материалдың пластикалық деңгейі, үлгінің кадрлық салыстырмалы ұзаруы және қалта мойынның қалдық салыстырмалы жіңішкеруі арқылы сипатталады. Бұл шамалар неғұрлым көп болса, материалдың пластикалық қасиеті жоғары.
Кадрлық деформацияның үлгідегі алғашқы ұзындығына қатынасы, кадрлық салыстырмалы деформация (δ) деп аталады. әртүрлі құрылымдық болат материалдары үшін, бұл шама 8:28% аралығында.

Мұндағы lүз үзілген үлгіні бір-біріне түйістіргендегі ұзындығы
Үзілген қимадағы үлгі ауданының өзгеруінің алғашқы көлденең қима ауданына қатынасы, үлгінің кадрлық салыстырмалы жіңішкеруі (Ψ) деп аталады.
Айтылған қатынас жоғары көміртекті морт болат үшін өте аз шамада болады, төменгі көміртекті болат үшін 60% аралығында.

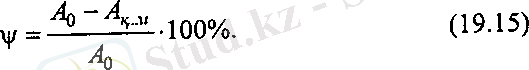
Мұндағы Ақ.м. үзілген ең жіңішке қимасының ауданы.
Серпімділік модулінің мәні болатын химиялық қосылысымен термиялық өңдеуіне айтарлықтай тәуелді емес.
Морт материалдар, мысалы шойын сығылғанда, алғашқыдан бастап Гук заңына бағынбайды, сондықтан, диаграмма қисық сызықты (19.10,а-сурет І қисық).

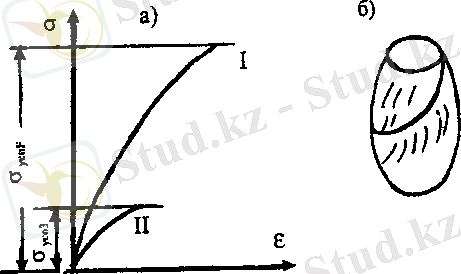
19.10-сурет
Шойынның созылу диаграммасы, сығылу диаграммасына ұқсас, бірақ беріктік шектерінде айырмашылықтары өте көп.
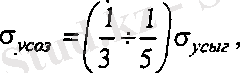яғни, шойын созылуға өте нашар жұмыс істейді. Шойын үлгі сығылғанда, өсіне шамамен 45° бұрыш жасайтын ең үлкен жанама кернеу әсер ететін ауданшаларға, параллель сызаттардың пайда болуынан қирайды (19.14,б-сурет).

Статикалық күштің жұмысы. Деформацияның потенциалдық энергиясы

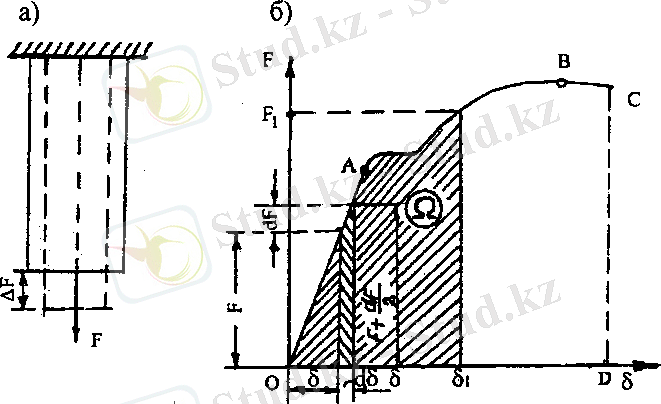
19.11-сурет
Білеу статикалық түрде әсер ететін F күшімен жүктелген (19.11,а-сурет). F күшінің әсерінен білеуде, бойлық деформация пайда болады, яғни білеудің күш әсері тұрған нүктесі орын ауыстырады, сондықтан F күші жұмыс істейді.
F күшінің әсерінен 19.11,б-суретте F, δ координата жүйесінде созылу диаграммасы тұрғызылған. Қандай да бір t уақытқа F күші мен δ орын ауыстыруының белгілі мәндері сәйкес келеді. Өте аз dt уақытта F күші dF-ке өссе, ал білеудің төменгі ұшы dδ жылжиды. Сонда F күшінің жұмысы

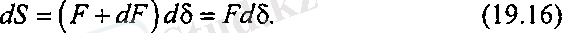
dFdδ екінші ретті аз шама болғандықтан ескерілмейді. (19.16) өрнегін F=0, F=F11 аралығында интегралдап, күштің толық жұмысын анықтаймыз.

Сонымен S жұмысы диаграмманың штрихталған бөлігінің ауданына, диаграмманың OABCD толық ауданы білеуді қиратуға кеткен жұмысқа тең.
F күшінің әсерінен, білеудегі кернеу пропорционалдық шектен аспаса Ω, табаны δ, биіктігі F, үшбұрыштың ауданына тең. Гук заңынан
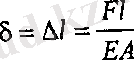, онда жұмыс

(19.18)-дегі F-тен құтылсақ

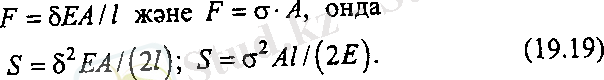
Кернеу, серпімділік шектен аспағанда, материалдың электромагниттік күйі ескерілмейді. Энергияның сақталу заңынан сыртқы күштің жұмысы толық потенциалдық энергияға (U)-ға айналады. Күш әсері тоқтағанда бұл энергия дененің алғашқы өлшемдері мен пішінін қалпына келтіруге жұмсалады, сонымен,

(19.18), (19.19) негіздерінде

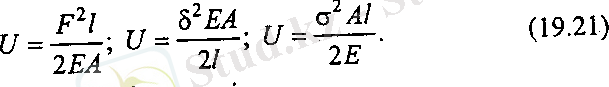
Соңғы өрнектегі A∙l= V білеудің көлемі, онда

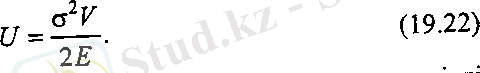
Формуланың екі жағын V-ға бөлсек, деформацияның меншікті потенциалдық энергиясы табылады.

Потенциалдық энергияның өлшем бірлігі, күш пен ұзындықтың көбейтіндісі, онда, меншікті потенциалдық энергияның өлшем бірлігі күшұзындық2.

Мүмкіндік кернеулер. Беріктікке есептеу

Құрылымдарды есептеудің негізгі мақсаты, оның қызметі барысында беріктігін қамтамасыздандыру.
Морт материалдан жасалған құрылымның барлық элементінде нақты кернеу, беріктік шегінен кем болса, беріктігі қамтамасыздандырылған. Құрылымдағы кернеуді, материалдың беріктік шегін дәл табу мүмкін емес (беріктік шектерін жуықтау әдістері арқылы анықтайды).
Құрылымдарды есептегенде, ең үлкен кернеу беріктік шегінен кем мәннен-мүмкіндік кернеуден аспауы тиіс. Беріктік шекті бірден артық қор коэффициенттеріне бөліп, мүмкіндік кернеуді анықтайды. Морт материалдар үшін беріктік шарт келесі түрде жазылады:

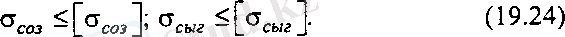
Мұндағы σсоз, σсығ - созылудағы, сығылудағы ең үлкен есептеу кернеулері, [σсоз, σсығ] - созылу мен сығылудағы мүмкіндік кернеулер.
Мүмкіндік кернеулер [σсоз, σсығ] материалдардың σусоз, σусығ беріктік шектеріне байланысты анықталады.

Мұндағы [пу] - мөлшерлі (қажетті) беріктік қор коэффициенті. Пластикалық материалдардың созылуындағы, сығылудағы беріктік шектері бірдей, олар үшін беріктік шарт.

Мұндағы σ құрылымдағы ең үлкен созушы немесе сығушы кернеу.
Пластикалық материалдар үшін мүмкіндік кернеу.

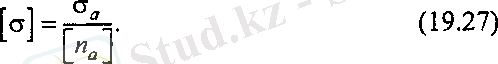
Мұндағы [па] - аққыштық шегіне қатысты мөлшерлі (қажетті) беріктік қор коэффициенті.
Пластикалық материалдарда кернеу, аққыштық шекке жеткенде, күштің аз ғана ұлғаюында деформация жылдам өседі, сондықтан мүмкіндік кернеуді анықтағанда, аққыштық шек қолданылады.
(19.24), (19.26) шарттары негізінде беріктікке есептеу, мүмкіндік кернеу арқылы есептеу деп аталады.
Пластикалық материалдардан жасалған кейбір құрылымдарда, кернеу аққыштық шекке жеткенде, әсер етуші күш айтарлықтай ұлғайғанда, деформация жылдам өспейді. Оларға статикалық анықталмаған және элементтері иіліп бұралатын жүйелер жатады. Мұндай құрылымдар мүмкіндік кернеу (19.24), (19.26) немесе шеткі күй арқылы есептеледі. Соңғы есептеуде, мүмкіндік күшті шеткі мүмкіндік күш деп атайды.
Құрылымның созылған немесе сығылған элементінің кез келген қимасы беріктік шартты қанағаттандыруы тиіс. Ол үшін ең үлкен созушы немесе сығушы кернеу пайда болатын қауіпті қиманы дұрыс таңдай білген жөн.
Білеудің ұзына бойы бойлық күш тұрақты болса, ең кіші көлденең қима қауіпті.
Құрылымды беріктікке есептегенде үш түрлі есептеулер кездеседі.
1. Кернеуді тексеру (тексеру есебі).
2. Қиманы таңдау (жобалау есебі).
3. Күш көтергіштігін анықтау (мүмкіндік жүкті анықтау).
Кернеуді тексергенде, көлденең қималардың аудандары А мен бойлық күш N белгілі. Қауіпті қимадағы кернеуді анықтап мүмкіндік кернеумен салыстырады.

Қимадағы таңдағанда, бойлық күш пен мүмкіндік кернеу белгілі. Таңдалатын аудан беріктік шартты қанағаттандыруы тиіс.

Жүк көтергіштікті анықтағанда, қиманың ауданы мен мүмкіндік кернеу белгілі. Осы шамалар арқылы, күштің мүмкіндік мәні [N] анықталады. []N=A[σ]. [N] мәні бойынша сыртқы күш табылады.
Беріктік қор коэффициенттерінің мәндері, құрылымдардың жауаптылығына байлансты тағайындалады. Жеке жағдайларда төмендетеді, машиналардың үйкелетін бөлшектерінің тозуын, корозия мен шіруін ескергенде, беріктік қор коэффициентін ұлғайтады.
Әртүрлі материалдар үшін беріктік қор коэффициенті келесі аралықтарда қабылданады.

Беріктік қор коэффициенттері мен мүмкіндік кернеулер, құрылымдарда жобалау нормативтеріне байланысты шектеледі. Машина жасау өндірістерінде мүмкіндік кернеулердің ішкі мөлшерлері бар.

Статикалық анықталмаған жүйелер
Берілген сыртқы күштің әсерінен, білеу мен топсалысырық жүйенің бойындағы ішкі күштер, тек статика теңдеулерімен табылса, жүйе стаикалық анықталған. Ішкі күштерді анықтауға статика теңдеулері жеткіліксіз жүйелер, статикалық анықталмаған деп аталады. Мұндай жүйелерді есептеу үшін, оның деформациясын сипаттайтын, (деформацияның біртұтастық теңдеулері) қосымша теңдеулер қажет. Айтылған теңдеулердің саны, жүйенің статикалық анықталмау дәрежесіне тең.
Статикалық анықталған жүйелердің элементтеріндегі ішкі күштер, тек сыртқы күштің әсерінен пайда болады. Статикалық анықталмаған жүйелердің элементтеріндегі ішкі күштер тек сыртқы күштердің әсерінен емес, температураның өзгеруінен, жеке элементтердің дәлсіздікпен жасалуынан, тіректің жылжуына т.с.с. себептерден де пайда болады.
Статикалық анықталмаған жүйелерді есептегенде, қосымша деформация теңдеулерін құру өте маңызды мәселенің бірі.

19.12-сурет
1. Екі ұшы қатаң бекітілген, көлденең қималарының аудандары А1, А2, А3 19.12-суретте көрсетілген білеуді қарастырайық. F күштің әсерінен тіректерде RB, RС реакциялары пайда болады. Барлық күштер бір түзудің бойында жатқандықтан статикадан тек бір теңдеу жазылады (19.12,а-сурет).

RB, RС белгісіздері бір теңдеуден табылмайды, қосымша тағы бір теңдеу қажет, онда жүйе бір рет статикалық анықталмаған болып есептеледі.
Қосымша теңдеуді құру үшін оның әсерін №№№ реакциясымен алмастырамыз (19.12,б-сурет).
F күшінің әсерінен тек оның жоғарғы деформацияланады, білеудің толық орын ауыстыруы FaEA1.
RB реакциясының әсерінен білеу толық деформацияланады, оның мәні үш аралықтың деформацияларының қосындысына тең.

Шындығында, білеудің төменгі бөлігі қатаң бекітілгендіктен, бұл қиманың орын ауыстыруы нөлге тең, онда

Жоғарыдағы теңдеулерден RB анықталады. Тірек реакциялары белгілі болғаннан соң, білеуді статикалық анықталған жүйе ретінде есептейді.
2. Шеткі екі сырықтарының өлшемдері бірдей болаттан, ортадағысы мыстан жасалған үш сырықтан тұратын жүйенің О нүктесі төрт күштің F, N1, N2, N3, әсерінен тепе-теңдік күйде болады. (19.13,а-сурет).

19.13-сурет
Күштердің соңғы үшеуі бойлық күштер - белгісіздер.
Теориялық механикдан белгілі бір нүктеде түйіскен жазық күштер жүйесі үшін, тек екі тепе-теңдік теңдеуі жазылады (Σx=0, Σy=0).
Белгісіздер теңдеулер санынан бірге артық жүйе, бір рет статикалық анықталмаған.
Статика теңдеулері келесі түрде жазылады (19.13,б-сурет).

Бірінші теңдеуден N1=N2 болатындығы ескеріліп, екінші теңдеу келесі түрде жазылады:

екі белгісізді бір теңдеу.
Қосымша теңдеуді жазу үшін жүйенің деформациясын қарастырамыз. F күшінің әсерінен үш сырық та ұзарып O нүктесімен төмен ауысады. N1=N2 және сырықтар бір материалдан жасалғандықтан бірінші, екінші сырықтардың ұзаруы ∆l1, ∆l2 өзара тең, сондықтан О нүктесі тік төмен түседі. Үшінші сырықтың ұзаруы, ∆l3.
Сырықтардың ұзаруы бір-біріне тәуелді, яғни деформациядан кейін де, олар
O1 нүктесінде түйіскен күйде қалады. Сырықтардың алғашқы ұзындықтарын ∆l1=OB1 мен ∆l2 =OC1 ұзарып жаңа ұзындықтары BB1, CC1 19.13,в-суретте бейнеленген. CC1 мен ВВ1 C және B нүктелерінің айналасында айналдырсақ, O нүктесінің жаңа орны O1 нүктесінде қиылысады. Деформация өте аз болғандықтан C1O, BO1 кесінділері CC1 мен BB1-ге перпендикуляр деп есептелінеді. Шеткі сырықтардың жаңа орны BO1, CO1 үзік сызықтармен көрсетілген, ортаңғы сырықтың ұшы O нүктесінде топсамен бекітілгендіктен, ол O1 нүктесіне көшеді, яғни OO1=∆l3 үшінші сырықтың ұзаруы.
Гук заңы бойынша сырықтардың ұзаруы ∆l, ∆l2, ∆l3, оларды созатын бойлық күшке тура пропорционал. 19.13,в-сызбасынан ұзаруларды бір-бірімен байланыстырсақ, қосымша деформацияның біртұтастық теңдеуін аламыз. O1B1O үшбұрышынан

∆l1, ∆l3-ті бойлық күштермен өрнектеу үшін, сырықтардың көлденең қималарының аудандары немесе олардың қатынастары белгілі болуы тиіс.
Сырықтардың көлденең қималарының аудандары А1, А2, серпімділік модульдері Еб, Ем онда

Бұл өрнектерді (19.33) қойсақ

BOD үшбұрышынан l3=l1cos∝ ескеріп,

Сонымен, N1 =N3 байланыстарын қосымша теңдеу алынды (19.34) өрнегін (19.32)-ге қойып

(19.34)-ден

Табылған өрнектерден бойлық күш N қима аудандары мен серпімділік модульдеріне тікелей байланысты емес, олардың қатынастарына тәуелділігі байқалады. n=A1A3 әртүрлі мәніне N1, N2, N3 әртүрлі мәндері сәйкес келеді.
Мүмкіндік кернеуімен табылған күштердің негізінде беріктік шарттан қиманың аудандары анықталады.

Бірінші шарттан А1 анықталып n=A1A3-тен, A3= A1п табылады.
Табылған мәндер (19.35)-нің екінші шартын қанағаттандыратындығына көз жеткізу керек, егер қанағаттандырмаса екінші шарттан, А3 анықталып, А1=пА3 табылады.4

Температуралық кернеу

Сыртқы күштің әсері жоқ болса да температураның әсерінен статикалық анықталмаған жүйелерде кернеу пайда болады. Мұндай жағдай температураның өзгеруінде де болады. Пісіріп қосылған рельстерде температуралық кернеу айтарлықтай. Бұл тұжырымды келесі мысалда көрсетейік.

19.14-сурет
Ұзындығы l, көлденең қимасының ауданы А, серпімділік модулі Е, сырықтың t температурады екі ұшы қатаң бекітілген. Температураның t2 өзгерткендегі кернеуді анықтау керек. (19.14-сурет) t2t1 болса, сырық ұзарып А, В тіректеріне қысым жасайды, ал тіректерден сырыққа реакция күштері әсерінен, ол сығылады. Статика теңдеуінен тіректерде реакциялар өзара тең, бірақ, сан мәні анықталмайды, жүйе статикалық анықталмаған. Ұштары бекітілген сырық температура әсерінен ұзындығын өзгертпейді, сондықтан, оның температура әсерінен ұзаруы ∝l∆t, тірек реакциялары әсерінен қысқаруына ∆lR-ге тең. Онда деформацияның біртұтастық теңдеуі келесі түрде жазылады.

Мұндағы, α сырық материалының сызықтық ұлғаюы коэффициенті

Екі ұшы қатаң бекітілген сырықтың бойындағы кернеу, оның материалының серпімділік модуліне, сызықтың ұлғаюы коэффициентіне және температурасының өзгеруіне ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.