Туынды ұғымын оқытуда тарихи мәліметтерді қолдану әдістемесі


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТІРЛІГІ
МАТЕМАТИКА, ФИЗИКА ЖӘНЕ ТЕХНОЛОГИЯЛАР ФАКУЛЬТЕТІ
Математика кафедрасы
КУРСТЫҚ ЖҰМЫС
Тақырыбы: ТУЫНДЫ ҰҒЫМЫН ОҚЫП ҮЙРЕНУДЕ ТАРИХИ МАҒЛҰМАТТАРДЫ ПАЙДАЛАНУ
МАЗМҰНЫ
КІРІСПЕ
1 МАТЕМАТИКАЛЫҚ ҰҒЫМҒА ЖАЛПЫ ТҮСІНІКТЕМЕ
1. 1 Математикалық ұғымдарды енгізудегі тарихи мағлұматтарды
тиімді пайдалану
2 ТУЫНДЫ ҰҒЫМЫН ЖӘНЕ ОНЫҢ ҚОЛДАНЫЛУЫН ОҚЫП
ҮЙРЕНУДЕ ТАРИХИ МӘЛІМЕТТЕРДІ ПАЙДАЛАНУ
- Туынды ұғымын пайдалануда тарихи мағлұматтарды қолдану
- Туынды оқыту әдістемесі
- Туындыға қолданылатын теоремалар
ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР
КІРІСПЕ
 Кез келген ғылымның негізін үйрену танымның нәтижелері жинақтаған ғылыми ұғымдар мен категориялардың жүйесін меңгеру болып табылады.
Кез келген ғылымның негізін үйрену танымның нәтижелері жинақтаған ғылыми ұғымдар мен категориялардың жүйесін меңгеру болып табылады.
Педагогика ғылыми ұғымдарды олардың таным үрдісіндегі гнесеологиялық және психологиялық маңызына сүйене отырып, білім мазмұнының басты құрылымдық бірлігі ретінде анықтайды.
Ғылыми ұғымдарды саналы да, терең меңгергенде ғана оқушылардың қоршаған дүниені толық, бүтін қабылдауларына жағдай туғызуға болады, жан-жақты өз бетінше және белсенді ойлайтын адам етіп қалыптастыруға болады.
Дүние таным өкілдері ұғым-мидың, материяның жоғарғы жемісі деп атап көрсеткен. Әр ғылым саласы бойынша пайда болған ұғым өзінің даму кезеңдерінде өзгеріссіз қалып қоймайды. Заттар мен құбылыстардың жаңа қасиеттер мен белгілерге ие болуы нәтижесінде ұғым мазмұны қоюланып, молая түседі, көлемі кеңиді, олардың қатыстары мен байланыстары толығырақ айқындалады.
Жұмыстың өзектілігі: математика оқыту барысында оқушылардың қай тақырыпты меңгеруге қиналатындығын анықтаудың маңызы зор. Оқушы қандай да бір тақырыпты өз дәрежесіне меңгере алмаса, соның салдарынан келесі өтілетін материалды түсінбей қалуы мүмкін. Туынды тақырыбын меңгеру және оны басқа ғылымдармен байланысын көре алудың маңызы зор.
Жалпы туынды ұғымына мына түрде анықтама беріледі:
 өсімшесінің
өсімшесінің
 өсімшесіне қатынасының, осы
өсімшесіне қатынасының, осы
 нольге ұмтылғандағы, шегі берілген
нольге ұмтылғандағы, шегі берілген
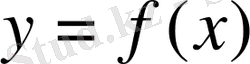 функциясының
х
нүктесіндегі туындысы деп аталады.
функциясының
х
нүктесіндегі туындысы деп аталады.
Курстың жұмыстың мазмұнын ашуға Исқақов, Көбесов, Колягин, Мишин және т. с. с. авторлардың еңбектері мен мақалалары қолданылды.
Жұмыстың зерттеу нысаны: туынды және оны оқып үйренуде тарихи мағлұматтарды қолдану әдістемесі.
Жұмыстың мақсаты:
- Оқыту процесінде оқушының санасына ғылыми теориялардың негізін қалаумен және оның туынды ұғымының қалыптастыру;
- Туынды және оның қолданылу әдістері мен идеяларын толық және терең түсінетін, оқушылардың қиындықтары әртүрлі есептерді шығару қабілеттерін дамытуға кепілдік беретін білімдер, іскерліктер мен дағдылардың жоғары деңгейіне қамтамасыз ету;
- Алынған білімдерді теориялық және тәжірибелік мәселелерді шешуге қолдана білу;
- Оқушыларды туынды және оның қолданылуын оқып үйренуде тарихи мағлұматтарды пайдалану, бұл ұғымды меңгеру арқылы ойлау қабілеттерін дамыту, тиімді жақтарын көре алу, пәнге деген қызығушылығын арттыру болып табылады.
Жұмыстың бағыттылығы: теориялық тарихи зерттеу арқылы.
Жұмыстың міндеті:
- Туынды ұғымын түсіну;
- Оны тәжірибеде қолдана білу;
- Тарихпен байланыстыра отырып түсіну;
- Оқушылардың туынды тақырыбын жетік меңгеруі.
Математикалық ұғымдарды дамыту мен оларды оқушылардың меңгеруін қамтамасыз ету мектеп математикасын оқытудың басты міндеттерінің бірі болып саналады. Ал бұл міндет мектеп математика курсының басты ұғымдарын саналы және баянды түрде таразылауды, соның негізінде көптеген дидактикалық міндеттерді шешуге болатын математикалық ұғымдарды меңгеруді қамтамасыз етуді, оларды оқушыларға оқытып- үйретудің тиімді жолдарын анықтауды қажет етеді.
Білімді меңгеру - ұғымдарды бүтін, тұтас күйінде меңгеру, ал ойлау ұғымдармен, пікірлермен жасалатын әрекет болып табылады. Орта мектеп математикасы бағдарламасының түсініктеме сөздігінде: “ . . . түсінікті де, мазмұнды мысалдар арқылы оқушыларға математикалық ұғымдардың дамуын көрсету керек, оларды ғылыми зерттеулердің кезеңдері және әдістерімен таныстыру керек” екендігіне баса назар аударылған.
“Оқушыларға жалпылау мен ұғымдарды қалыптастыру мектептегі оқытудың ең басты мақсаттарының бірі”, - деп атап көрсеткен В. В. Давыдов. Осыған орай математикалық ұғымдарды дамытудың тиімді жолдарын іздестіру - оқыту мен тәрбиелеудің сапасын көтеруге бірден - бір құрал болып табылады.
Философтар мен қоғамдық ғылым өкілдері де ұғымдардың дамуында тәжірибенің ролін зор екендігіне баса назар аударған. Өздеріңмұң - мұқтаждарын, қажеттіліктерін қанағаттандыру қызметтерінің нәтижесінде ғана, адамдар санасында алғашқы ұғымдар пайда болған. Адамдардың тәжірибелік қызметіне қажет болған шындық дүниесінің сандық қатыстары мен кеңістіктегі формаларын бейнелеу үшін алғашқы математикалық абстракциялық ұғымдар туындалады. Бұған күні бүгінге дейін қолданылып жүрген математикалық терминдердің өзі дәлел бола алады. Мысалы, “трапеция” - гректің сөзі: ”тамақтанатын үстел” дегенді білдіреді, ”симметрия ” - грек сөзі: “біркелкілік, өлшемділік; ”хорда” - грек сөзі: ”шек”; ”цилиндр” - грек сөзі: ”айналдырамын”, “домалатамын”; ”вектор” - латынша: ”апарушы” немесе ”сілтеуші” т. с. с. Математикалық ұғымдардың ең алғашқысы және түп қазығы - сан ұғымы. Сан ұғымы өте ертеде адамзат жазу - сызу білмеген заманда пайда болған А. Көбесов сан ұғымының қалыптасуына алдымен санау амалы себепші болғандығын көрсетеді. Адам саннан бұрын “санауды”, ”түгендеуді” білген. Санау, түгендеу әрекеті негізінде сан ұғымы туады, біртіндеп кеңейеді. Ежелгі қазақтар төрт түлік малдарын санамай-ақ түгендеуі - осының нақты мысалы. Біздің ата - бабаларымыз бір қора қойдың өзін жасына қарай бөліп, әрбір төлді түстеп түгендейтін болған.
Сырттай үстірт қарағанда математикалық ұғымдар тым абстрактілі, жасанды, тәжірибемен еш байланысы жоқ, қоғамдық үрдіске тигізетін әсері жоқ секілді болып көрінуі мүмкін. Ал математикалық ұғымдарға тарих көзімен қарасақ, олардың пайда болуы мен дамуына терең талдау жасасақ, жағдай күрт өзгереді. Ұғымдар терең мәнге, бай мазмұнға толықтырылады, математикалық ұғымдардың жалпылығына, логикалық жинақтылығына, өмірде және тәжірибеде кеңінен қолданылатындығына оның нәтижелерінің өзі - ақ куә болады.
Танымның диалектикалық заңдылықтарына сүйене отырып, математикалық ұғымдарды меңгеруде, ұғымға сәйкес термин сөздермен, символдармен жүйелі түрде мақсатқа бағытталған жұмыс жүргізу керектігін, оқушылардың математикалық ұғым мен білімдерді саналы және белсенді меңгерулерін басқару мүмкіндігін ескеріп, ғылыми - әдістемелік деңгейін ашып көрсетелік.
Оқушыларға жаңа енгізілген термин және символдың тарихи - генетикалық құрылымымен таныстыру. Бұл оқу мазмұны адамгершілікке, оқушылардың "Неге бұл ұғым осындай атпен аталады, неге басқаша аталмайды?” деген сияқты сұрақтарына жауап берудің тәрбиелік және ғылыми мәні бар. Мәселен, (
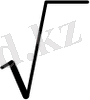 ) таңбасы латынша "radix" сөзінің бірінші әрпі негізінде алынған. Сол сияқты процент белгісі латынша "procentum" сөзін итальяндар "pro cento" түрінде қабылдаған, біртіндеп тез жазу және қысқарту нәтижесінде cto болып, кейін % символы пайда болған. Пирамида латын сөзі, қазақша жалын деген мағынаны береді. Шындығында да, пирамида жанып тұрған жалын формасы сияқты. Медицинада қолданылатын пирамидон дәрісі, сонымен қатар күнделікті өмірде қолданылатын примус та сол мағынаны береді.
) таңбасы латынша "radix" сөзінің бірінші әрпі негізінде алынған. Сол сияқты процент белгісі латынша "procentum" сөзін итальяндар "pro cento" түрінде қабылдаған, біртіндеп тез жазу және қысқарту нәтижесінде cto болып, кейін % символы пайда болған. Пирамида латын сөзі, қазақша жалын деген мағынаны береді. Шындығында да, пирамида жанып тұрған жалын формасы сияқты. Медицинада қолданылатын пирамидон дәрісі, сонымен қатар күнделікті өмірде қолданылатын примус та сол мағынаны береді.
Оқу материалының мазмұнын әртүрлі мүмкіндіктер арқылы орындау үшін, мұғалімге ең алдымен оны меңгеріп қана қоймай, сонымен қатар оның негізгі тарихи этаптарын білген жөн.
Математикалық ұғымдарды енгізудегі тарихи мағлұматтарды тиімді пайдалану үшін:
- Ұғымның шығу тарихы туралы жалпы түсінік болу қажет.
- Ұғымды нақты анықтап, қажет кезде пайдалана білу керек.
- Әрбір ұғымның анықтамасын біле отырып, оның жеке қасиеттерін, түрлерін ажырату, яғни елеулі белгілерін айқын нақты анықтау.
Тарихи деректермен таныстыру сабақ түсіндіру басында 1-2 минуттан аспауы керек. Сабақты қалыпты емес, тың әдістерді қолданып, тарихи деректермен толықтырып отырса, оның нәтижелілігі жоғары болмақ. Оқушыларға тарихи деректер арқылы түсіндіру, олардың осы ұғымға деген зейінін аударып қана қоймай, сол ұғымға деген қызығушылығын арттырады.
2. туынды ұғымын оқып үйренуде тарихи мәліметтерді пайдалану
2. 1. Туынды ұғымын пайдалануда тарихи мағлұматтарды қолдану
Туындылар және олардың функцияларды зерттеуде қолданылуы қарастырылатын математиканың бөлімі дифференциалдық есептеу деп аталады. Айырманы көрсететін
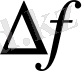 түріндегі өсімше туындылармен жұмыс істегенде елеулі орын алады.
түріндегі өсімше туындылармен жұмыс істегенде елеулі орын алады.
«Туынды» термині derivee деген француз сөзінің қазақша сөзбе-сөз аудармасы, оны 1797 ж. Жозеф Луи Лагранж (1736 - 1813) енгізген, қазіргі кездегі
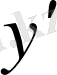 ,
,
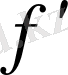 белгілеулерін де сол енгізген-ді. Бұл атау мынадай ұғымның мағынасын ашады:
белгілеулерін де сол енгізген-ді. Бұл атау мынадай ұғымның мағынасын ашады:
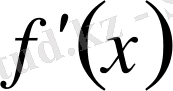 функциясы
функциясы
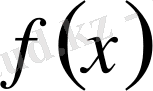 -тен шығады,
-тен шығады,
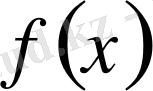 -тің туындысы болып табылады. И. Ньютон функцияның туындысын флюксия деп, ал функцияның өзін флюента деп атаған. Г. Лейбниц дифференциалдық қатынас туралы айтқан және туындыны
-тің туындысы болып табылады. И. Ньютон функцияның туындысын флюксия деп, ал функцияның өзін флюента деп атаған. Г. Лейбниц дифференциалдық қатынас туралы айтқан және туындыны
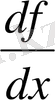 түрінде белгілеген. Бұл белгілеу қазіргі әдебиетте де жиі кездеседі. Лейбниц
түрінде белгілеген. Бұл белгілеу қазіргі әдебиетте де жиі кездеседі. Лейбниц
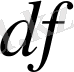 символын
символын
 функциясының дифференциалын белгілеу үшін таңдап алған.
функциясының дифференциалын белгілеу үшін таңдап алған.
 функциясының
функциясының
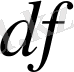 дифференциалы -
дифференциалы -
 туындысының
туындысының
 өсімшесіне көбейтіндісі, яғни
өсімшесіне көбейтіндісі, яғни
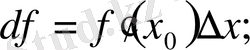
 белгілеуін
белгілеуін
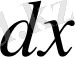 -пен алмастырып, оны былай да жазуға болады:
-пен алмастырып, оны былай да жазуға болады:
 осыдан
осыдан
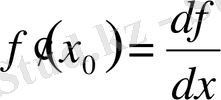 .
.
Дифференциалдық есептеуді Ньютон мен Лейбниц біршама беріректе, XVII ғасырдың соңында құрды. Туынды туралы ғылымды жүйелі дамытып, олар анализдің екі проблемасын тұжырымдады:
- Жүретін жолдың тұрақты (яғни кез келген уақыт мезетіндегі) ұзындығы берілген; көрсетілген уақыт ішіндегі қозғалыс жылдамдығын табу керек.
- Қозғалыс жылдамдығы тұрақты берілген; көрсетілген уақыт ішінде жүрілген жолдың ұзындығын табу керек.
Бірінші ахуал дифференциалдық есептеудің даму бағдарламасына береді.
Ньютон механика есептерін негізге алса (ньютондық анализ ньютондық классикалық механикамен қатар жасалған-ды), Лейбництің артықшылығы ол геометрия есептерін негіз етіп алды.
Анализ идеяларының одан кейінгі дамулары туралы айтқанда (ол идеялар өте тез тарап кетті және өзіне көптеген ізбасарлар тапты) Лейбництің шәкірттері - ағайынды Я. Бернулли және И. Бернуллилердің есімдерін алдымен атаған жөн.
Негізі де, көрсеткіші функция болып келетін дәрежелік-көрсеткіштік функцияның туындысы Ньютонда да, Яков Берниллида да жоқ. Оны Лейбниц пен Иоганн Бернулли тағайындаған. Дифференциалдық есептемедегі анықталмаған өрнектерді шын мәндерін Иоганн Бернулли көрсеткен. Дифференциалдық теңдеулер теориясында
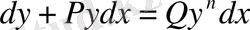
теңдеуі Бернулли теңдеуі деп аталады. Оны 1695 жылы Яков Бернилли ұсынған.
Иоганн Бернуллидың ғалымдарға жазған хаттарында да құнды мағлұматтар кездеседі. Оларда бір тектес дифференциалдық теңдеулердің
 ауыстырмасы арқылы айнымалылары айырылатын теңдеулерге келтірілетіндігі, осы күні Лагранж теңдеуі деп аталатын
ауыстырмасы арқылы айнымалылары айырылатын теңдеулерге келтірілетіндігі, осы күні Лагранж теңдеуі деп аталатын
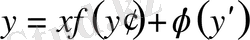
теңдеуінің шешілетіндігі, көптеген шектеусіз қатарлар айтылады.
А. Лопиталь (1661 - 1704) И. Бернуллиден дәріс алған, ол 1696 жылдың өзінде дифференциалдық есептеудің алғашқы курсы «Қисық сызықтарды зерттеуге арналған шексіз аздар анализін» баспадан шығарып үлгерді, бұл жаңа әдістердің таралуына септігін тигізді.
Бұл салада ірі нәтижелерге жеткен Лагранж еді, оның еңбектері анализ негіздерінің мән-мағынасын түсінуде зор роль атқарды. Лейбниц пен Ньютон қалдырған математикалық анализ Лагранжды қанағаттандырмаған, ол анализді қайта құруды көздеген. Анализдің ең негізгі ұғымдарының бірі - туынды ұғымы. Туынды ұғымы түсінікті түрде, айқын, тұжырымдалса, интеграл да, басқа ұғымдар да оңай тұжырымдалады. Туындыны штрих арқылы белгілеуші Лагранж болған
Туындылар таблицасы бойынша дифференциалдар таблицасын жасауға болады. Мысалы,
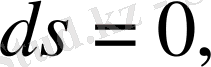
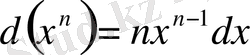 т. с. с.
т. с. с.
Дифференциалдың да геометриялық мағынасын (1 сурет) анықтауға болады. Координаталар системасына
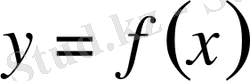 функциясының графигін салайық, оның бойынан
функциясының графигін салайық, оның бойынан
 және
және
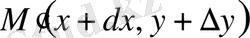 нүктелерін алайық.
нүктелерін алайық.
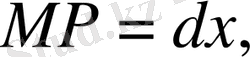
 болады.
болады.
 нүктесінен жанама жүргізсек, ол
нүктесінен жанама жүргізсек, ол
 түзуін бір
түзуін бір
 нүктесінде қиып өтеді. Туындының геометриялық мағынасы бойынша
нүктесінде қиып өтеді. Туындының геометриялық мағынасы бойынша
 бұрышының тангенсі
бұрышының тангенсі
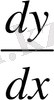 туындыға тең.
туындыға тең.
 үшбұрышынан
үшбұрышынан
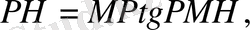 яғни
яғни
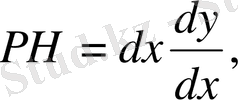

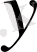 Equation. 3
M
1
Н
Equation. 3
M
1
Н
M Р
y
0
x
x=dx
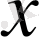 Equation. 3
Equation. 3
1 сурет
Сөйтіп, функцияның
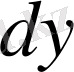 дифференциалы жанау нүктесінің х абциссасы есептеудің
дифференциалы жанау нүктесінің х абциссасы есептеудің
 өсімше қабылдағанда жанаманың оған сәйкес нүктесінің ординатасы қабылдайтын өсімше болып табылады.
өсімше қабылдағанда жанаманың оған сәйкес нүктесінің ординатасы қабылдайтын өсімше болып табылады.
 кесіндісі функция өсімшесінің екінші бөлігі, яғни жоғары ретті шектеусіз
кесіндісі функция өсімшесінің екінші бөлігі, яғни жоғары ретті шектеусіз
 шама болады. Сонымен, дифференциалдың геометриялық мағынасы - қисыққа жүргізілетін жанаманың бұрыштық коэффициенті.
шама болады. Сонымен, дифференциалдың геометриялық мағынасы - қисыққа жүргізілетін жанаманың бұрыштық коэффициенті.
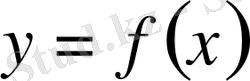 функциясынын дифференциалданғанда
функциясынын дифференциалданғанда
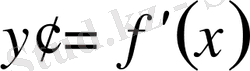 туындысы шығады. Оны бірінші ретті туынды деп атайды. Бірінші ретті туындыны тағы да дифференциалдасақ, бірінші ретті туындының туындысын табамыз. Ол екінші ретті туынды деп аталып, екі штрих арқылы белгіленеді:
туындысы шығады. Оны бірінші ретті туынды деп атайды. Бірінші ретті туындыны тағы да дифференциалдасақ, бірінші ретті туындының туындысын табамыз. Ол екінші ретті туынды деп аталып, екі штрих арқылы белгіленеді:
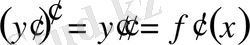 .
.
Үшінші, төртінші т. с. с. ретті туындылар да бола береді. Үшінші ретті туынды. Төртінші, бесінші т. с. с. ретті туындыларда штрих орнына рим цифлары немесе жақшаға алынған үнді цифлары жазылады. Мәселен:
y VI - алтыншы ретті туынды,
y (38) - 38-нші ретті туынды,
y n - n-нші ретті туынды.
Бұлар кейде былай да белгіленеді:
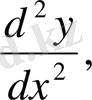
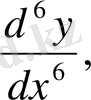 Equation. 3
Equation. 3
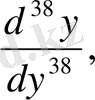 Equation. 3
Equation. 3
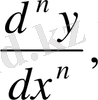
оқылуы "дэ екінші игрек бөлінген дэ икс квадрат" т. с. с.
Туындының ретін функцияның дәрежесімен шатастырмау керек. Олар екі түрлі ұғымға жатады.
Екінші, үшінші ретті т. с. с. ретті туындылар жоғары ретті туындылар деп аталады. Жалпы түрде:
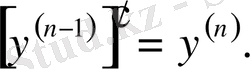
Мысал 1.
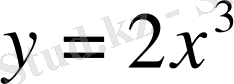 -тің жоғары ретті туындыларын табыңыз.
-тің жоғары ретті туындыларын табыңыз.
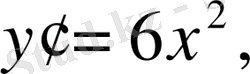

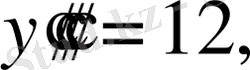
y IV =0 .
Бұдан кейінгі туындылардың бәрі де нольге тең болады.
Екінші ретті туындының механикалық мағынасы бар: егер
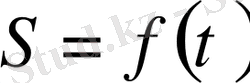 функциясы қозғалыстың математикалық заңы болса, жолдың екінші ретті
функциясы қозғалыстың математикалық заңы болса, жолдың екінші ретті
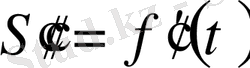 туындысы үдеуді өрнектейді. Сондықтан үдеу жылдамдықтың туындысы болып табылады.
туындысы үдеуді өрнектейді. Сондықтан үдеу жылдамдықтың туындысы болып табылады.
Мысал 2.
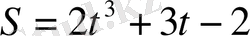 , жол берілген.
, жол берілген.
 болғанда үдеуді табыңыз.
болғанда үдеуді табыңыз.
Шешуі:
 -ке тең болады.
-ке тең болады.
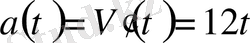 болса, онда
болса, онда
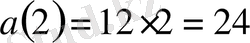
Жауабы:
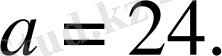
2. 2 Туындыны оқыту әдістемесі
Қазіргі қазақ тіліндегі «жылдамдық», орыс тіліндегі «скорость», француз тіліндегі «витессе», ағылшын тіліндегі «спид», неміс тіліндегі «гешвиндигкайт» сөздері «тау», «тас», «су» сияқты ертеден келе жатқан ескі сөздер емес, бертін жасалған туынды сөздер. Итальян, поляк, үнді, араб, монғол т. б. тілдерде де солай. Дүниеде жылдамдық мағынасында қолданылатын термині жоқ тілдерде кездеседі. Жылдамдық - техниканың даму дәрежесінің ең негізгі көрсеткіштерінің бірі. Тоқу фабрикасындағы ұршық секундына 45 рет айналады. Реактивті ұшақ сағатына 2500 километр жер «қусырады». Жасанды спутник Жер шарын 88 минутта айналып шығады . . . Жылдамдықты анықтайтын сандар фабриканы, ұшақты, спутникті, т. с. с. сипаттаумен қатар, соларды жасап шығарған елдер мен халықтардың ғылыми мен мәдениетін де сипаттайды.
Ежелгі заман орта ғасырларда жылдамдық жөнінде айқын ұғым болмаған, жылдамдық көбінесе жол ұзындығымен, үдеумен шатастырылған. Мәселен, ғасырда жазылған кітаптардың бірінде: «Керуен Дунай өзенінен Сырдарияға дейін төрт ай жүреді» делінген. Мұнда тіпті жолдың ұзындығы да белгісіз. Дунай еуропаның жартысын шарлап келіп, Қара теңізге құяды. Орта Азия жерінің біразын суарып, Аралға құятын Сырдария да сондай. Қай қаладан қай қалаға шейін? Неше шақырым немесе фарсаң? Ол кезде уақытты өлшейтін маятникті немесе серіппелі сағаттар да болмаған. «Жылдамдық» термині Аристотель мен Архимедтің шығармаларында да кездеспейді. Бұл ұғым Винчи еңбектерінен басталды деуге болады. ұлы итальян ғалымы Леонардо да Винчи (1452-1519) әр түрлі машиналардың қозғалыстарын және құстардың ұшу мүмкіндіктерін зерттеген, ұшақ алғашқы проектісін жасаған. Алайда жылдамдықты механиканың негізгі ұғымдарының бірі ретінде ғылыми тұрғыдан алғанда алғаш рет тұжырымдаушы Галилей боды. Жылдамдық туралы есеп, жанама есебімен қатар, туынды ұғымын қалыптастырды.
Дене бір қалыпты v жылдамдықпен қозғалса, t уақыт ішінде түзу сызықтың бойымен s=vt жол жүретіндігі мәлім. Бірақ дүниеде бір қалыпты түзу сызықты қозғалыс болмайды. Бір қалыпты түзу сызықты қозғалыс - есептерді оңайлату үшін қолданылатын шартты түрдегі теориялық ұғым. Кейде жылдамдығының өзгерісі өте аз шама болатын немесе өте аз уақыт ішінде болған қозғалысты, жуық түрде, бір қалыпты деп ұйғарып, есепті қарапайым жағдайға келтіруге болады. Көп жағдайда v орнына қозғалыстың орташа жылдамдығы алынады. 120 километр жолды 2 сағатта жүріп өткен машинаның орташа жылдамдығын «сағатына 60 километр» дейді. Орташа жылдамдық 60 км/сағ болғанымен, машина жолдың кейбір жерлерін сағатына 10, 30, 50, 80 километр жылдамдықпен жүріп өтуі мүмкін.
Орташа жылдамдық механикалық қозғалыстар теориясында елеулі роль атқарады. Бірталай есептер сол арқылы шешіледі. Алайда оның қажетті мағлұматтарды бере алмайтын кезі де болады. Машина көпір үстінен құйғытып өтіп, қозғалыстың жол полициясы тағайындаған ережесін бұзды, көпірге зақым келді. Мектеп жанынан тежеусіз өтіп балаларды қағып кетті . . . Осындайда машинаның дәл көпірден өткен кездегі, мектеп жанынан өткен кездегі жылдамдықтарын білу қажет. Математика тілінен айтқанда уақыттың кез келген t кезіндегі жылдамдықты анықтау керек.
Дененің жүріп өтетін s жолы қозғалыс болатын t уақытқа тәуелді келеді. Сондықтан жол уақыттың функцциясы болады: s=f(t) .
Бұл теңдік әдетте қозғалыстың математика заңы деп аталады.
Дене әуелі
t
уақыт, содан кейін
 уақыт қозғалған болсын. Берілген математикалық заң бойынша ол
t
уақытта
s
,
уақыт қозғалған болсын. Берілген математикалық заң бойынша ол
t
уақытта
s
,
 уақытта
уақытта
 s
жүреді. Сонда:
s
жүреді. Сонда:
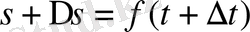 ,
,
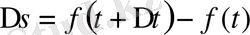 .
.
Соңғы теңдікті өсімшесіне бөлеміз:
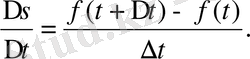
Осы қатынастың
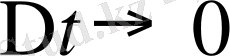 болғандағы шегі қозғалыстың уақыт
t
болған кездегі жылдамдығы деп аталады. Ол
v
әрпімен белгіленеді (
v
- французша «
болғандағы шегі қозғалыстың уақыт
t
болған кездегі жылдамдығы деп аталады. Ол
v
әрпімен белгіленеді (
v
- французша «
 » - «жылдамдық» деген сөздің бірінші әрпі) . Егер айтылып отырған қатынастың тиянақты шегі болмаса, жылдамдық та болмайды. Сөйтіп,
» - «жылдамдық» деген сөздің бірінші әрпі) . Егер айтылып отырған қатынастың тиянақты шегі болмаса, жылдамдық та болмайды. Сөйтіп,
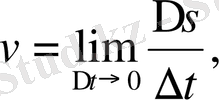
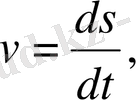
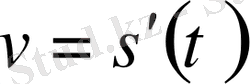
Мысал үшін, жоғарыдан құлаған дененің жылдамдығын қарастырайық. Бұл қозғалыстың Галилей тағайындаған заңы
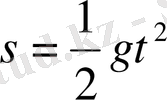 формуламен өрнектеледі,
формуламен өрнектеледі,
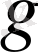 - ауырлық күшінің тұрақты үдеуі,
s
функциясы
s(t)
жолдың қысқаша жазылған түрі. Сонда:
- ауырлық күшінің тұрақты үдеуі,
s
функциясы
s(t)
жолдың қысқаша жазылған түрі. Сонда:
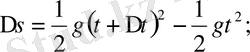
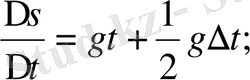
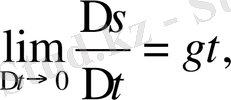
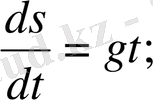

Демек, жоғарыдан құлаған дененің жылдамдығы уақытқа пропорционал болады. Бұл заңды да Галилей тағайындаған.
Жанама мен жылдамдық жөніндегі есептер туынды ұғымына алып келді. Кейін бұлардан басқа да көптеген есептердің туынды арқылы шешілетіндігі анықталды. Мәселен, өткізгіштің көлденең қимасынан өтетін электр шамасының уақыт бойынша алынатын туындысы ток болады, жылу шамасының температура бойынша алынатын туындысы жылу сыйымдылық болады т. с. с. зерттей келгенде сан алуан мәселелердің кілті туындыда болып шықты. Сондықтан есептерді жеке-жеке қарастырмай, жанама есебі, жылдамдық есебі, ток есебі т. с. с. деп бөліп-жармай, туындыны жалпы түрде зерттеу қажет болды.
Алдымен туындының жалпы анықтамасын тұжырымдап алайық.
 өсімшесінің
өсімшесінің
 өсімшесіне қатынасының, осы
өсімшесіне қатынасының, осы
 нольге ұмтылғандағы, шегі берілген
нольге ұмтылғандағы, шегі берілген
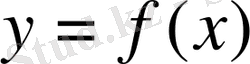 функциясының
х
нүктесіндегі туындысы деп аталады.
функциясының
х
нүктесіндегі туындысы деп аталады.
Анықтама бойынша:
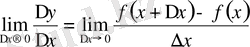
Әдетте бұл туындының
 немесе
немесе
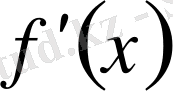 немесе
немесе
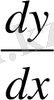 деп белгіленетіндігі алдыңғы тақырыпта айтылған.
деп белгіленетіндігі алдыңғы тақырыпта айтылған.
Келтірілген анықтамадан туындыны табу үшін төмендегідей «төрт сатыға көтерілу» қажеттігі көрінеді.
Бірінші саты. Тәуелсіз айнымалыға өсімше беріп, функцияның өскен мәнін табу керек:
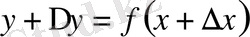 .
.
Екінші саты. Функцияның өсімшесін табу керек:
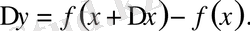
Үшінші саты. Функцияның өсімшесін тәуелсіз айнымалының өсімшесіне бөлу керек:
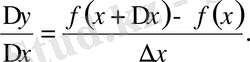
Төртінші саты.
 өсімшесін нольге ұмтылтып, соңғы қатынастың шегін есептеу шығару керек, сол шек туынды болады.
өсімшесін нольге ұмтылтып, соңғы қатынастың шегін есептеу шығару керек, сол шек туынды болады.
Әр түрлі функциялардың туындыларын есептеп шығарғанда, яғни функцияларды дифференциалдағанда, төмендегі алты ереже жиі қолданылады. Алты ереже мынандай түрде беріледі:
I. Тұрақты шаманың туындысы нольге тең болады.
Бір
С
тұрақты шаманы, жалпылық үшін, функция ретінде қарастырып,
 десек, оның «өскен» мәні бәрі бір
десек, оның «өскен» мәні бәрі бір
 болады. Бұдан
болады. Бұдан
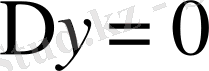 . Сондықтан,
. Сондықтан,
 қандай болса да,
қандай болса да,
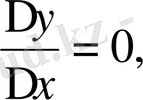
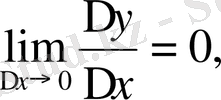
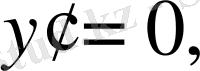
 болғандықтан, мұны кейде былай жазады:
болғандықтан, мұны кейде былай жазады:

II. Тұрақты көбейткішті туындының алдына шығарып жазуға болады.
 ал
ал
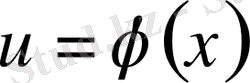 болса (
болса (
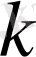 - тұрақты көбейткіш),
- тұрақты көбейткіш),
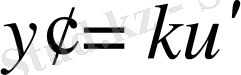 болады. Шынында да:
болады. Шынында да:
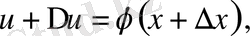


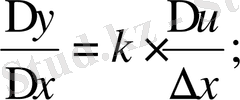


III. Алгебралық қосындының туындысы сол функциялардың туындыларының сәйкес алгебралық қосындысына тең болады.
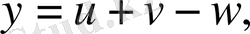 ал
ал
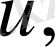
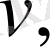
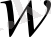
өздері х -ке тәуелді функциялары болсын. Сонда:
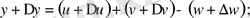
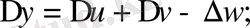
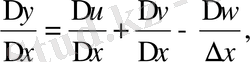

IV. Екі функцияның көбейтіндісінің туындысын табу үшін бірінші функцияның туындысын екінші функцияның өзіне көбейтіп, содан соң екінші функцияның туындысын бірінші функцияның өзіне көбейтіп, шыққан екі көбейтіндінің қосындысын алу керек.

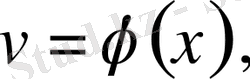
ал
 болсын.
болсын.
Сонда:
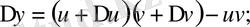
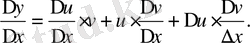
Енді теңдіктің екі жақ бөлігінен де шек аламыз. Соңғы мүшеден,
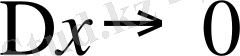 болғанда,
болғанда,
 және
және
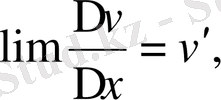 демек,
демек,
 болады. Сондықтан
болады. Сондықтан
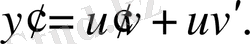 Мұны былай да жазады:
Мұны былай да жазады:
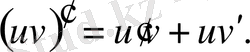 Көбейткіш функциялардың саны бірнешеу болғанда да осы ереже қолданылады:
Көбейткіш функциялардың саны бірнешеу болғанда да осы ереже қолданылады:
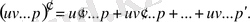
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz