Ондық бөлшектер

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Жоспар

Кіріспе

Ондық бөлшектер

Қысқартылмайтын бөлшек - ондық бөлшекке тең болады

Қорытынды

Пайдаланған әдебиеттер:

Кіріспе

Таза периодты шексіз ондық бөлшек алымы оның периодына, ал бөлімі периодта қанша цифр болса, сонша тоғыздықтан тұратын сан болатын жай бөлшекке тең;

Бүтін бөлігі нөлге тең болатын аралас периодты шексіз ондық бөлшек алымы екінші период басталғанға дейінгі цифрлардан тұратын сан мен бірінші период басталғанға дейінгі цифрлардан тұратын санның айырмасы, ал бөлімі периодта қанша цифр болса сонша тоғыздықтардан және бірінші период басталғанға дейін қанша цифр болса, сонша нөлдерден тұратын жай бөлшекке тең.

Ондық бөлшектер

Анықтама. Ондық бөлшектер деп позициялық ондық санау жүйесінде жазылған, бөлімдері 10-ның дәрежесіне тең болатын жай бөлшектерді, яғни $\frac{m}{10^{n}}$ (мұндағы m, nϵN) түріндегі бөлшектерді айтады. Айталық, бөлшектің алымының ондық жазылуы мынадай: т=т _к . . . т ₀ болсын, яғни

т=т _k 10 ^k + т _k-1 10 ^k-1 + . . . +т ₀

Сонда, n≤k болғанда дәрежелерге амалдар қолдану ережесі бойынша:

Натурал т _k 10 ^k-n +… т _n санын М деп белгілейік. Сонда $\frac{m}{10^{n}}$ бөлшегін былай жазу қабылданған: M, т=т _n-1 . . . т ₀

Сонымен $\frac{m}{10^{n}}\$ бөлшегін жазып көрсетуде т санының ондық жазылуының соңғы n цифрын үтірмен айырады. Егер бөлшектің алымындағы санның таңбалануындағы цифрлар саны n-нен кем болса, онда оның алдына цифрлар саны n+1 болғанға дейін нөлдер жазады да, шыққан санның соңынан бастап n цифрдан соң үтір айырады.

Анықтама. Ондық бөлшекте үтірден кейін орналасқан цифрлар ондық таңбалар деп аталады.

Аныңтамадан келіп шығатын ондық бөлшектердің I бірнеше қасиеттерін атап көрсетейік.

Ондық бөлшектің жазылуында қатар тұрған екі цифрдың сол жағындағысының разрядтың бірлігі оң жағындағысына қарағанда он есе артық болады.
Ондық бөлшекті 10kсанына көбейту үтірді оңға қарайкцифрға жылжыту, ал оны 10kсанына бөлу үтірдіI солға қарай к цифрға жылжыту арқылы жүзеге асырылады.
Ондық бөлшекке нөлдер тіркеп жазғаннан және ондық бөлшектің соңындағы нөлдерді алып тастағаннан оның мәні өзгермейді, яғни натуралт, пжәнеsсандары қандай болса даm10n\frac{m}{10^{n}}және10sm10n+s\frac{10^{s}m}{10^{n + s}}белшектері тең болады.
Екі ондық бөлшекті ортақ бөлімге келтіру үшін олардың ондық таңбалары кемінің соңына, олардың ондық таңбалары бірдей болатындай етіп нөлдер тіркеп жазу жеткілікті.
Екі ондық бөлшектің қайсысының бүтін бөлігі артық болса, сол артық болады. Бүтін бөліктері тең болатын екі ондық бөлшектің тең емес ондық таңбаларының ішіндегі біріншісі қайсысында артық болса, сол ондық бөлшек артық болады.

Кез келген - $\ \ \frac{m}{n}$ (m, nϵN) түріндегі бөлшекті ондық бөлшек түрінде жазуға болама?

Қысқартылмайтын бөлшек - ондық бөлшекке тең болады

Теорема. Қысқартылмайтын бөлшек - ондық бөлшекке тең болуы үшін, оның бөлімінің жай көбейткіштерге жіктелуіне тек 2 немесе 5 сандарының енуі қажетті және жеткілікті болып табылады. Мысалы: - бөлшегін ондық бөлшек түрінде жазуға болады. Себебі бұл қысқармайтын бөлшек және бөлімін жай көбейткіштерге жіктесек оның құрамында тек 2 және 5 сандары бар: 80 = 2 ⁴ • 5.

Мысалы:

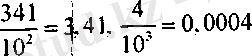
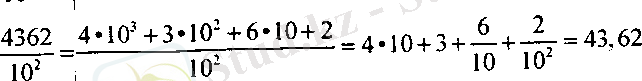
73. Шексіз периодты ондық бөлшектер

Қысқартылмайтын $\frac{p}{q}$ бөлшегі түрінде өрнектелетін a санын ондық бөлшекке айналдыру үшін натурал р санын натурал q санына бөлу керек.

Бұл жағдайда пайда болатын қалдықтар q -дан кем, яғни мына 0, 1, 2 . . . , q -1 түріндегі сандар болатыны өзінен - өзі айқын.

Егер бөлу процесінің белгілі бір қадамында қалдық нөлге тең болса, онда бөлу аяқталады да а = $\frac{p}{q}$ , санының ондық жазылуы ондық таңбалардың шектеулі тізбегімен, яғни шектеулі ондық бөлшекпен өрнектеледі. Егер әрбір қадамда пайда болатын қалдықтардың барлығы нөлден өзгеше болса, онда бөлу ешқашан аяқталмайды. Шынында да, әр түрлі қалдықтар саны шектеулі болатындықтан белгілі бір қадамнан бастап қандай да бір қалдық қайталанады, демек бөліндіде цифрлар қайталана бастайды. Осылайша қайталанатын цифрлар период құрайды. Бұл жағдайда р -ны q - ға бөлу процесі шексіз болады және а = $\ \frac{p}{q}$ санының ондық жазылуы ондық таңбалардың шексіз тізбегімен, яғни шексіз ондық бөлшекпен өрнектеледі. Сонымен бірге осының нәтижесінде шығатын шексіз ондық бөлшек периодты болады және нәтижеде қандай да бір орыннан кейін белгілі бір цифрлар тобы шексіз қайталанып отырады.

Мұндай бөлшекті қайталанатын цифрлар тобын жақшаға алу арқылы жазып көрсетеді және қайталанатын цифрлар тобын бөлшектің периоды деп атайды. Мысалы:

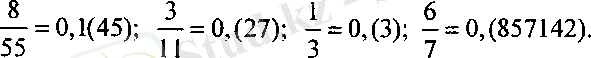
Периоды үтірден кейін басталатын бөлшектерді таза периодты бөлшектер, ал үтір мен период арасында басқа ондық таңбалары болатын бөлшектерді аралас периодты бөлшектер деп атайды. Мұндай бөлшектердің периодында тоғыздық болмайтындығын ескертеміз.

Егер қысқартылмайтын бөлшектің бөлімінің жай көбейткіштерге жіктелуіне 2 және 5 сандары енбесе, онда бұл бөлшекті ондық бөлшекке айналдырғанда таза периодты бөлшек, ал егер бөлімнің жіктелуіне 2 немесе 5 көбейткіштері енетін болса, онда аралас периодты бөлшек шығады (үтір мен периодтың басталу аралығында 2 мен 5 көбейткіштерінің ең үлкен дәреже көрсеткіші қанша болса, сонша цифр болады) . Жалпы алғанда, егер - бөлшегі қысқартылмайтын бөлшек болса және оның бөлімінің жіктелуінде 2 мен 5-тен өзгеше жай көбейткіш болса, онда - бөлшегі шексіз периодты ондық бөлшекпен, ал бөлімнің жіктелуіне тек 2 және 5 сандары ғана енетін болса, онда - бөлшегі шектеулі ондық бөлшекпен өрнектеледі.

Жоғарыда айтылғандардан мынадай қорытынды жасауға болады: кез келген оң рационал сан не шектеулі ондық бөлшекпен не шексіз периодты ондық бөлшекпен өрнектеледі.

Шектеулі ондық бөлшектерді олардың, оң жағына нөлдер тіркеу арқылы шексіз бөлшек түріне келтіруге болады. Шектеулі ондық бөлшекті периоды нөлге тең шексіз ондық бөлшек деп есептеуге келісейік.

Онда кез-келген оң рационал сан шексіз периодты ондық бөлшек түрінде өрнектеледі деп айтуға болады. Сондай-ақ, кері тұжырым да дұрыс болады: кез келген оң шексіз периодты ондық бөлшек қандай да бір оң рационал санды білдіреді.

Енді кері мәселені қарастырайық: шексіз периодты ондық бөлшекті ңалай жай бөлшекке айналдыруға болады?

Айталық, периодты 0, /24 / бөлшегі берілсін. Оған сәйкес болатын санды а деп белгілейік, онда а = 0, 242424 . . .

Егер үтірді оңға ңарай екі орынға жылжытсақ, а саны 100 есе артады, яғни 100 а =24, 24 24 Немесе 100а=24+0, 24 24 . . . Сонымен 100 а = 24+а. Соңғы теңдеуді шешсек а = $\frac{22}{99}$ немесе а = $\frac{8}{33}$ бұдан 24 санының бір мезгілде $\frac{22}{99}$ бөлшегінің алымы және 0, /24 / бөлшегінің периоды екенін байқау оңай.

Енді айталық периоды 0, 7/61/, яғни 0, 76161 . . . бөлшегі берілген делік. Оған сәйкес болатын рационал санды b деп белгілейік. Сонымен b=0, 76161 Егер үтірді оңға қарай бір орын жылжытсақ b саны 10 есе артады, яғни 106=7, 6161 . . . Енді х=7, 6161 . . . деп белгілейік. Егер соңғыда үтірді екі орын оңға жылжытсақ, онда х саны 100 есе артады да, 100 х=761, 6161 . . . немесе 100х=761+0, 6161 . . . Теңдіктің екі жағынада 7-ні қоссақ, 100х+7=761+7, 6161 . . . Ал 7, 6161 . . . =x деп келіскен едік, олай болса 100х+7=761+х:. Бұдан х= $\frac{761 - 7}{99}$