Дискретті кездейсоқ шамалар мен ықтималдық үлестірулері: Бернулли, биномдық, геометриялық және гипергеометриялық үлестірулер


Мазмұны
Кіріспе . . . 6
I. Тарау. Ықтималдылық туралы түсінік
1. 1. Кездойсоқ шамалардың түсініктемесі . . . 7
1. 2. Ықтималдылықтың орташа және дисперсия үлестірілуі . . . 11
1. 3. Бернулли үлестіруі . . . 13
II. Тарау. Биномальды үлестіру
- Геометриялық үлестіру . . . 22
- Гипергеометриялық үлестіру . . . 25
ІІІ. Қорытынды . . . 30
ІУ. Пайдаланылған әдебиеттер . . . 31
К і р і с п е
Қазіргі уақытта ықтималдықтар теориясы барлық жаратылыстану, экономикалық және техникалық ғылымдар ғана емес, тіпті математикадан алшақ деп саналатын тіл ғылымына, педагогика мен психологияға, сондай-ақ социологияға, археологияға еніп, ортақ тіл табысып, ішкі құрылыс заңдарын ашатын пәрменді құралға айналып келеді кеңейтіліп, анықтала түседі де, формальданады. Оқиға ұғымы ықтималдылықтың . Ықтималдықтар теориясының бірінші негізгі ұғымы- оқиға бірте-бірте классикалық анықтамасында бастапқы ұғым болып, формальды логикалық тұрғыдан анықталмайтын жиын ұғымы ретінде түсіндірілсе, аксиоматикалық тұрғыдан оған анықтама берілді. Сондықтан оқиға ұғымы туралы мына жағдайларды ескеру қажет. Оқиғалар мен олардың арасындағы қатыстарды үш рет қайталап отырғанымызды аңғару қиын емес.
Ықтималдылық формальданған, бұл жағдайда ықтималдықтың классикалық, статистикалық (жиіліктік), , геометриялық және аксиоматикалық анықтамалары бір-бірімен салыстыру және жетімсіздігін толықтыру арқылы түсіндіріледі.
Негізгі теоремалардың дәлелдемесі ықтималдылықтың классикалық анықтамасы негізінде келтірілді. Комбинаторика ұғымы қарапайым статистикалық мәліметтер арқылы сипатталады. Мұнда қайталама және қайталанбайтын таңдаамалар сияқты статистика терминдерін енгіземіз. Комбинаторика ұғымы ықтималдықтарды есептеуге кең қолданылады.
Ықтималдық ұғымдарының тарихи дамуы мен ғыылым ретінде қалыптасуы бірнеше сатыдан өтеді. Бұл ғылымның дамуына Европа ғалымдары Б. Паскаль (1623-1662), П. Ферма (1601-1665), Х. Гьюгенс (1629-1695), Я. Бернулли (1654-1775), А. Муавр (1667-1754), П. Лаплас (1749-1827), Ф. Гаусс (1777-1855), С Пуассон (1781-1840) және орыс ғалымы Буяковский (1804-1889) көп үлес қосты.
Кездойсоқ шамалар және ықтималдылықты үйлестіру.
Кездойсоқ шамалардың түсініктемесі .
Математика және статистикадан мамандандыратын жетекші университеттің студенттерінен, олардың мектепте елу тақырыптың шамасында оқыған тақырыптарын атап көрсетуді сұраған. Студенттердің жартысына жуықтары «биномиалды үлестіру» тақырыбын және беп пайызы «дискретті кездойсоқ шамаларды» атаған.
Алайда, екінші тақырыпты оқымай, білмей, бірінші тақырып жайында түсіну мүмкін емес.
Кездойсоқ шамалар дегеніміз-жазықтықта айнымалы шамалардың тек қана бір мәні ғана әр нүктеге тура келетін сандық айнымалы болып табылады (оны функция түрінде сипаттаған дұрыс) .
Таңдамалы жазықтық көпмүшелік болып табылатын
{1, 2, 3, 4, 5, 6} ойын сүйегін лақтырумен байланысқан сынаманы қарастырдық. Қарапайым мысалды алу үшін Х-тың мәнін кездойсоқ шама ретінде анықтау «ойын сүйегінде түскен соң» жеткілікті. Х-1, 2, 3, 4, 5 және 6 мәндерін қабылдаулары мүмкін. Ойын сүйегін екі реттілікте лақтырумен байланысқан тәжірибесінде түскен мәндердің соммасы және әрбір бүтін мәндер 2-ден 12-ге дейін таңдап алынған жазықтық тордағы нүктелер саны саналған, яғни шын мәнісінде кездойсоқ шамалардың мүмкін болтын мәндері қарастырылған.
Кей жағдайларда кездойсоқ шамаларды тиісті формуламен «бөліп» қарастырған тиімдірек болады. Екі реттілікте ойын сүйегін лақтырудың В-жайындағы «мәннің жетіге тең түсу соммасы», ал С-жағдайында «мәннің сегізге тең түсу соммасы» анықталған. Егер Х-кездойсоқ шамасы «түскен мәндер сомасы» ретінде анықталса, онда Х=7 жағдайы В-жағдайына Х=8 ал ол С жағдайына дәлме-дәл ұқсас келеді (осыған, байланысты айта кету, қажет, кездойсоқ шама жағдай, оқиға бола алмайды) . Әлі де В және С жағдайларына ұқсас тоғыз жағдай бар. Жинақталған осы он бір жағдайлар барлық таңдап алынған жазықтықты құрайды, ал бөлек түрде олар түскен шама, мәндерге байланысты жазықтықты бөледі.
Дискретті таңдап алынған жазықтық-нүктелердің шектеулі сандарынан немесе «шексіз сомаларды» нүктелердің көпмүшеліктерінен тұрады, мысалы бүтін барлық оң сандардың көпмүшелікері.
Шексіз таңдап алынған осы жазықтыққа қарама-қарсылық жазықтықтың кез-келген шекті интервалындағы нүктелердің шексіз сандарынан тұрады; шексіз таңдап алынған жазықтықта бақылау қарастырылған шексіз, үздіксіз деректерді береді. Үздіксіз таңдап алынған жазықтық және үздіксіз кездойсоқ шамалар қарастырылады.
Дискретті таңдап алынған жазықтықта анықталған кез-келген кездойсоқ шама-дисскретті кездойсоқ шама деп аталынады. Бірқатар жағдайлардың ықтималдығы - осы жағдайларды құрайтын ықтимал мәндердің соммасы болып табылады. Ойын сүйегі екі реттілік лақтыру жағдайында атап өткендей, таңдап алынған жазықтықтың барлық 36 нүктесі тең ықтималды. Сондықтан таңдап алынған жазықтық кездойсоқ Х- шамасымен бөлінетін он бір жағдайдың ықтималдығы 1/36 -осы жағдайды құрайтын таңдап алынған жазықтықтың нүктелер санына тең.
Дискретті кездойсоқ мәндердің ықтималдығын үлестіру тиісті ықтималдылықтармен бірге кездойсоқ шамалардың көпмүшеліктерін білдіреді. Х-кездойсоқ шамасының ықтималдығын үлестіру мына төмендегідей түрде көрсетіледі.
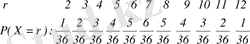
Осы таңдап алынған жазықтың өзінде Х-кездойсоқ шамасын анықтай аламыз «түскен шамалар айырмасы». Бұл жерде таңдап алынған жазықтықтың алты нүктесі бар, Y=0, Y=1 тең оң нүкте және тағы басқалары. Ықтималдылықтарды үйлестіру, тарату 18 сан бөлгішімен ұсынған тиімдірек:
52 картадан тұратын қорабынан қайталамай екі картаны кездойсоқ таңдап алу тәжірибесі үшін Х-кездойсоқ шамалардың ықтималдыдылқтарын үлестіру Х={алынған тұздардың саны} Х=0 48*47 нүктесіне тең таңдап алынған жазықтықтарға тиісті анықталады, «бірінші карта тұз» жағдайы үшін 4*48 нүкте сай келеді, «екінші карта тұз» жағдайы үшін 4*48 нүктесі және Х=2 жағдайында 4*3 нүктесі сай келеді. Таңдап алған жазықтықта барлығы 52*51 нүкте бар, сондықтан Х үшін ықтималдылықты үйлестіру келесі түрде болады:
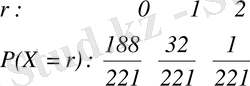
Y=0 кездойсоқ шама үшін ықтималдылықты бөлу «Алынған ликтер соңы» мына төмендегідей болады.
Ықтималдылықтарды графикалық бөлу жиіліктер түріндегі деректер үшін вертикалды кесінділер диаграммасы түрінде ұсынылуы мүмкін. Оқырман үшін осындай қосымшаларды өз беттерінше жасауға мүмкіншілік береді. Ол осы тарауда қарастырылады.
Х-кездойсоқ шамасының үлестірудегі кумулетивті функциясы F(X<x) түрінде анықталады. Х-тан функция түрінде өрнектелген шама кездойсоқ шама кез-келген берілген Х-санынан төмен немесе тең болатынын белгілеуге арналған жазба әріптерін қолданудағы және мәнде үшін алынған қатар әріптер айырмашылықтарына назар аударыңыздар: х-пен кез-келген алгебралық есептеулер орындалса, ол Х-пен орындала алмайды. Сонымен қатар, бұл F(x) функциясының анықтамасы үздіксіз және дискретті кездойсоқ шамалар үшін қолданбалы. Тек қана бүтін, толық мәндерді қабылдайтын дискретті кездойсоқ шамалар үшін F(r) функциясы ықтималдары суммалаумен алынуы мүмкін:
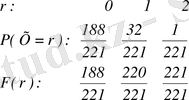
Жалпы жағдайда былай жазуға болады:
F(x) функциясы барлық Х затты шамалары, мәндері үшін анықталған, тіпті Х- кездойсоқ шама тек қана бүтін мәндерді қабылдаса да. Осы мысал үшін F(x) фунц иясының толық жазбасы мынадай: егер, Х және Y - тек қана толық, бүтін мәндерді қабылдап, таңдап алынған жазықтықтан анықталатын болса екі дискретті кездойсоқ шамалар тәуелсіз, байланыссыз деп айтылады, егер:
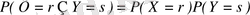
Тәуелсіз кездойсоқ шамалар толық анықталуы біркелкі үздіксіз кездойсоқ шамалар үшін де және дискретті шамаларға да қолданбалы. Х және Y тәуелсіз, егер
кез келген затты х және у үшін.
Осындай түрлі түсініктерді «тәуелсіз жағдайлар», «тәуелсіз сынамалар», «тәуелсіз кездойсоқ шамалар» нақты білу және түсіну ықтималдылықтың қарапайым теориясын терең түсінудің негізі болып табылады.
Орташа және ықтималдылықты үлестіру дисперсиясы.
Біз N бақылау жиынтығынан орташа және дисперсияны анықтадық.
Бірқатар тізбекті бағдарламалар, жиіліктер түрінде ұсынылған деректермен жұмыс істеуге бейімделген. Егер h-ты, түрлі бақылау мәндерін
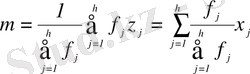 ,
,
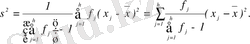
Деректер арасындағы бақылау сандарының өсу шегі бойынша барлық мүмкін болатын мәндер пайда болады, ал қатынасты жиіліктер шекті қатынасты жиіліктерге ұмтылады. Ол
Мұндағы екі жағдайда суммалау барлық
Соңғы формулада
Жақында қаралатын стандартты ықтималдылық үлестірулер үшін
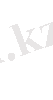
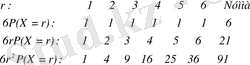
жағдайдағылар таңдап аынған тұздар саны үшін екі картаға алатынымыз:
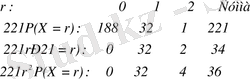

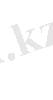
Бернулли үлестіруі
Бұл тарауда, біз ықтималдылықты жеті түрлі типтермен байланысқан есептеу бағдарламаларын ұсынғалы отырмыз. Мысалы, «Биномальды бөлу» жайлы айтқанда шын мәнісінде дискретті кездойсоқ шамалар ға арналған, солатрға қолданылатын үлестірудің ерекше түрін қарастырады. Бірқатар тәжірибелерге сәйкес келетін нақты үлестіру деректі тәжірибенің сандық сипаттамаларының бір немесе бірнеше түрлеріне тәуелді. Оқу құралдарында «параметр» сөзі көптеген жағдайларда «жиынтықты, жинақталған сандық сипаттама» түрінде «статистиканы» анықтай отырып айқындалады. Бұл термин үлестіруге қолданылады.
Үлестірудің барлық жеті, реттік сандық қатарлары бойынша ұсынылады. Ол, осындай бағдарламаларды «ықтималдылықты дискретті үлестіру» деп аталатын біркелкі пакетіне жинақтауға мүмкіндік жасайды. Бірінші бағдарламаға барлық пакет үшін «меню» белгіленген. Бұл тізімде жеті үлестіру түрі зерделеп - зерттелуі мүмкін, ыңғайлы болу үшін алфавиттік қатарда орналастырылған.
Қарапайым үлестіру түрі болып-Бернулли үлестіруі болып табылады. Ондағы кездойсоқ шама екі кіріспеден тұратын таңдап алынған жазықтықта анықталған. Тиісті сынақтар жүргізілетін типті таңдап алынған жазықтықтарды көрсетеміз:
{герб, тор} {жарамды, жарамсыз},
{бала, қыз} {дәл тию, қисық кету},
{қабылданды, қайтарылды } {өлім, жазылу},
Осы көрсетілген жағдайларда «жеңіс, табыс» және «жеңіліс» көріністері көрсетілген . Х-кездойсоқ шамасын табыс саны ретінде анықтаймыз, олай болса Х 0 және 1 мәндерін қабылдауы тиісті. Алайда, «табыс » сөзі бақылаушының міндеті жарамсыз, сапасы бар бұйымдарды тауып алу және сондықтан да «жарамды» сөзі «жеңіліске», ал «жарамсыз» сөзі «табысқа» теңестіріледі.
Результат выполнения программы символы, таңбасы, «жетістік, табыс» ықтималдығын белгілеу үшін қолданылады және осы дара параметр үлестіруді толығымен анықтайды. Жоғарыда қаралған жүйеге қарай отырып орташа және дисперсия мәндерін алу қиын емес:
Айта кетелік, бастапқы және орталық моменттері, бақылау
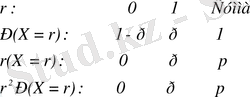
\[\mu=p.\]\[\sigma^{2}=p-\ p^{2}=p(\,I-\ p\,)=p q\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,q=I-p\]
нәтижесінде алынған деректі моменттерге ұқсас ықтималдылықтарды үлестіру үшін анықталады. Ол
Алайда, осындай қарапайым сынақтағы «сәтсіздік» ықтималдылығы
Арқылы белгіленеді. Онда
Программа 1.
100 REM Дискретные распределения вероятностей
110 PRINT:PRINT : PRINT “1. Бернулли распределение”
120 PRINT:PRINT “2. Биномиальное распределение”
130 PRINT:PRINT “3. . Геометрическое распределение”
140 PRINT:PRINT “4. Гипергеометрическое распределение”
150 PRINT:PRINT “5. Отрицательное биномиальное распределение”
160 PRINT:PRINT “6. Пуассоновское распределение”
170 PRINT:PRINT “7. Равномерное дискретное распределение”
200 PRINT:PRINT:PRINT “Какой тип распределение”
210 PRINT “Вам нужен?”
220 PRINT:PRINT “Нажмите 1, 2, 3, 4, 5, 6 или 7”
230 D=VAL(GET$)
240 ON D GOTO 1000, 2000, 3000, 4000, 5000, 6000, 7000.
1000 REM Бернулли распределение
1100 PRINT:PRINT:PRINT “Бернулли распределение”
1110 PRINT:PRINT“Х есть число успехов в одном”
1120 PRINT “испытании Бернулли с вероятностью”
1130 PRINT “успеха р. ”
1140 PRINT:INPUT “Хотите ли вы ввести p в виде дроби?(Y/N) ”; A$
1150 IF A$=’’N’’THEN PRINT:INPUT “Введите р”; GOTO 1170
1160 PRINT:INPUT “Введите числитель, затем знаменатель”; А, В;
P=A/B
1170 G=1-P: V\P*G
1200 PRINT:PRINT “Среднее=p”; P
1210 PRINT “Дисперсия=”; V
1220 PRINT “Стандартное отклонение=; ” SQR(V)
1300 W=G:Y=W
1400 PRINT
1420 PRINT:PRINT” r p(X=r) ”; TAB(21) ; “P(X<=r) ”
1430 PRINT :PRINT ”r P(X=r) ”; TAB(21) ; “P(X<=r) ”
1430 PRINT
1440 FOR I= 0 ТО 1
1460 PRINT “”; “ ”; W; TAB(20) ; Y
1480 W=P:Y=Y+W
1490 NEXT I
1510 PRINT: PRINT “Чтобы вернуться к началу, нажмите R”
1520 R$= GET$
1530 IF R$= “R” GOTO 1100
Ескерту.
- 110-210 қатарларында «меню» ұсынылады, ол жерде бір немесе екі үлестіруді қосу үшін бос орын бар.
- 230 -240 қатарларында қиындықтар болса, онда екінші программаға қараңыз.
- Әр үлестіру түріне, тиісті келетін тәжірибе түрлері мен кездойсоқ шамалар жайлы ақпараттар басылымға берілу керектігі жайлы ережені ұстанамыз. Бұл түсіндірмелерді түсінбейтіндер бағдарламамен жұмыс істеулеріне болады.
- Р-ның шамасын түбір түрінде енгізу басқа да бірқатар бағдарламаларға қосылуы мүмкін.
- 1200-1220 қатарлары 2200-2220, 3200-3220 стандартталған қатарлармен құрастырылған. Бұл жердегі мақсат түрлі бағдарламалардың логикасын, ой-өрісін салыстыруды қысқарту, бір бағдарламадан басқа бағдарламаға қатарларды көшіруді жеңілдету және ұқсас бөлімдерді бөлек, шағын бағдарламаға біріктіру.
Биномиальды үлестіру
N тәжірибесіндегі тізбектелген табыстар, жетістіктер санын, мөлшерін санау талап етілсе, олардың әрқайсысы р- жетістік ықтималдығына ие болып, басқа қалған сынақтарға тәуелді болмаса, онда тиісті кездойсоқ шама биномиальды үлестіруге ие болады. Үлестіру параметрлері n және p шамалары, көп жағдайларда қысқартылған
Жалпы жағдайда,
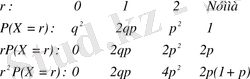
Бұл жағдайда, Бернулли үлестіруіндей
\[q=I-p\]белгіленуі қолданылады. Егер сынаманың тәуелсіздігін және тәуелсіз жағдай үшін ықтималдылықты көбейту ережесін қолдантын болсақ үлестіру формуласын алу да қарапайым.
 \[2\,p q+2\,{\cal p}^{2}=2\,p(\,q+p\,)=2\,p\]
\[2\,p q+2\,{\cal p}^{2}=2\,p(\,q+p\,)=2\,p\]және
\[2\,p q+\mathcal{U}^{2}=2\,p(\,q+2\,p\,)=2\,p(\,I+p\,)\]
Мұнда
Жалпы айтқанда, биномиальды үлестіру тәуелсіз кездойсоқ шамалардың n суммасын үлестіру болып табылады. Олардың әрқайсысы р параметрлі Бернулли үлестіруіне ие. Яғни, Бернулли үлестіруі дегеніміз-
n=1 және n=2 үшін алдын ала алынған нәтижелермен осы формулалардың келісілетін көру жеңіл. Барлық үлестіруді тез есептеуде маңызды роль атқаратын
тиісті формуланы

Программа 2.
2000 REM Биномиальное распределение
2010 Z$=””:CF=0. 5
2100 PRINT:PRINT:PRINT “Биномиальное распределение”
2110 PRINT:PRINT “X есть число успехов в n”
2120 PRINT “испытаниях Бернулли, каждое из которых”
2130 PRINT “имеет вероятность успеха р. ”
2135 REM при n=1 получается распределение Бернулли.
2136 REM если n велико, А р мало, то Х приближенно имеет
2137 REM распределение Пуассона со средним, равным n*р.
2140 PRINT:INPUT “Введите n, p”; N, P
2150 Q=1-P:FL=0
2160 M=N*P:V=M*Q
2200 PRINT:PRINT “Среднее=”; M
2210 PRINT “Дисперсия=”; V
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz