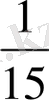Сандар мен бөлшектер: шығуы, дамуы, түрлері және арифметикалық амалдары


Мазмұны
Кіріспе 2
- Сандардың шығуы және оның дамуы 4
- Бөлщек түрлері 8Жай бөлшек 8Ондық Бөлшек 11Периодты Бөлшек 15Үздіксіз бөлшек 18
- Бөлшектің теңдігі. Бөлшектің негізгі қасиеті.
Бөлшектерді қысқарту 20
Қорытынды 22
Пайдаланған әдебиеттер 23
Кіріспе
Бөлшек, арифметикада -бірліктің (бір бүтіннің) бір не бірнеше тең үлестерінен құралған сан. Ол (немесе м/н) белгісімен өрнектеледі, мұндағы м - Бөлшектің алымы, ол бірліктен алынған үлес санын көрсетеді, ал н - Бөлшектің бөлімі, ол бірліктің тең бөлікке бөлінгендігін көрсетеді. Бір санды екінші санға бөлгеннен шығатын сан бөлінді деп аталады. Алымы бөлімінен кіші Бөлшек дұрыс Бөлшек деп, ал алымы бөліміне тең не одан үлкен Бөлшек бұрыс Бөлшек деп аталады. Бөлімі 10 санының бүтін дәрежесі болатын Бөлшек ондық бөлшек деп аталады. Ондық Бөлшек бөлімсіз жазылады. Оның бөлімінде қанша нөл болса, алымының оң жағынан сонша цифр (орын) үтір арқылы ажыратылады. Мысалы, (ал тізбекті Бөлшек жайлы үзіліссіз бөлшек) . Бөлшек туралы алғашқы түсінік ежелгі Вавилонның ескілікті жазуларында кездеседі. Вавилондағы, яғни бөлімі 60-тың дәрежесі болатын Бөлшектің ежелгі арифметикада ерекше маңызы болған. Бірлікті 60 және 3600 = 602 үлеске бөлу әдісі қазіргі кезге дейін сақталған. Мысалы, сағат не градус 60 мин-қа (), ал әрбір минут 60 с-қа бөлінеді. Бөлшекке амалдар қолдану әдісі Мысырдағы Ахмес папирусында (б. з. б. 2000 - 1700 ж. ) кездеседі. Онда Бөлшекті тек түрінде ғана болады деп есептеп, кез келген бөлшекті өзара тең бөлшектердің қосындысы түрінде жазуды ұсынған. Мысалы, бөлшектің осы заманғы белгіленуі ежелгі үнділерде пайда болған. “Бөлшек” термині Еуропаға 1202 жылы арабтардан Леонардо Пизанскийдің еңбегі арқылы енген.
Адамзат тарихында «сан» ұғымы өте ерте қалыптасты.
барлық натурал сандар жиынында қосу, көбейту амалдары ғана орындалады, бірақ азайту амалы әрқашан орындала бермейді. Мысалы, 5-12=х, х
. Бұдан сан ұғымын кеңейту қажет болды.
Енді барлық теріс бүтін сандарды және ноль санын біріктіріп, жаңадан барлық бүтін сандар жиынын
алайық. Бұл жиында қосу, көбейту, азайту амалдары орындалады, бірақ бөлу амалы үнемі орындала бермейді. Мысалы, 3:5=х, х
тағы да сан ұғымын кеңейту қажет болды.
Енді
түріндегі, мұндағы
ЕҮОБ(p, q) =1 барлық бөлшектер жиынын алайық. Мұндай бөлшектер жиынын барлық рационал сандар Q жиыны дейді.
Мысалы, кез келген шаршыны диогоналы оның қабырғасымен өлшемдес емес, яғни квадраты 2- ге тең болатын рационал сан жоқ.
Ондай санды иррационал сан дейді және ол жиынды J әріпімен белгілейді.
Рационал сандар Q жиыны мен иррационал сандар J жиынын біріктіріп барлық нақты сандар Q
J=R жиынын аламыз.
Бөлімдері 10 сандарының көбейтіндісі алымдары натурал сандар болатын
,
,
бөлшектерін қарастырайық. Бөлімдерін 10 санының дәрежелері түрінде жазуға болады. Демек, берілген сандардың әрқайсысы үшін мына теңдіктер:
,
,
,
орындалады.
Мұндай сандар жалпы түрде былай өрнектеледі:
, мұндағы h=10, ал
,
, …
- әрқайсысы 0-ден 9-ға дейінгі цифрлардың бірі.
Бөлімі 10 санының дәрежесі болатын бөлшекті ондық бөлшек дейді. Қысқармайтын бір жай бөлшекті, мысалы
бөлшегін, қарастырайық. Оны ондық бөлшекке айналдыру қажет болсын. Ол үшін бөлшектің алымын бөліміне бөлеміз, нәтижеде
… шектеусіз ондық бөлшек шығады.
- Сандардың және бөлшектердің шығуы және дамуы
Карл Гаусс математиканың сан салаларына сарапқа сала келіп арифметиканы математиканың патшасы деп бағалаған. Ал арифметиканың негізгі ұғымы - сан. Ендеше, сол сан ұғымының қалай пайда болуын ашу, білу - ғылыми методологиялық үлкен мәселе.
Сан туралы ұғым адамзат мәдениетінің тууымен және оның дамуымен тығыз байланысты. Шынында, егер осы ұғым болмаса, өзіміздің рухани өміріміз бен практикалық қызметімізді тиісті дәрежеде көрсете алмас едік. Есеп - қисап жүргізу, уақыт пен қашықтықты өлшеу, еңбек нәтижесінің қорытындысын есептеу сан ұғымынсыз мүмкін емес.
Сан әуел баста заттарды санаудың қажеттілігінен туған математикалы ұғымдардың бірі. Кейін ол математикалық білімнің дауына қарай жетілдірілді. Бұл ұғым өте ерте заманда адамдардың практикалық қызметтерінінен қажеттілігінен келіп туды.
Жалпы алғанда сан ұғымы басқа ешқандай емес тек шындық дүниеден шыққан . Өте ерте заманда пайда болған сан ұғымы көптеген ғасырлар бойы жалпыланып, кеңейе түсті . Сонда сан жайындағы түсініктер адамзаттың практикалық мұқтаждығына, мәселен, шамаларды өлшеудің қажеттілігіне және математиканың өзінің ішкі мұқтаждығына байланысты кеңеіәп отырғандығы байқалады. Мысалы шамаларды дәлірек өлшеудің мұқтаждығы оң бөлшек ұғымының тууына себепті болса, теңдеулерді шешу тәжірибелері мен осы санаудағы теориялық зерттеулерге байланысты теріс сандар пайда болды. Бастапқыда санның жоқ екенін белгілеу үшін қолданылған нөл саны теріс сандар енгізілгеннен кейін сан ретінде қарастырылатын болды.
Француз математигі Рене Декарт (1596-1650) 1637 жылы координаталық түзуді енгізіп теріс және оң сандарға түсінік берді.
-3 -2 -1 0 1 2 3
Нөл саны, натурал сандар және оған қарама -қарсы сандар бүтін сандар жиынын құрайды. Оны Z әріпімен белгілейді. Ал бүтін сандар жиыны және теріс бөлшектер рационал сандар жиынын құрайды. Рационал сандар жиынын Q әріпімен белгілейді. Рационал термині латын тіліндегі «ratio» деген сөзден шыққан. Ол қазақшаға аударғанда «бөлінді», «қатынас» деген мағынаны береді. Яғни бұл жерде рационал сан бүтін сандардың қатынасы деп түсіндіріледі. Мысалы 7=7\1 ; 7=14\2; 7=28\4
Бұлар бөлшек сандар. Жалпы рационал сан ұғымы әртүрлі шамаларды - ұзындықты, салмақты . ауданды, перимеитрді және тағы сол сияқты өлшеу процесіне байланысты пайда болды.
Нәрселерді санауда пайдаланылатын сандарды натурал сандар деп аталады. Натурал сандар қатары 1 санынан басталады. Оның мүшелері шексіз болады. Натурал сандар ұғымының дамуы ерте заманада адамдардың заттар жиынтнғының санын оларды санамай-ақ, яғни өзара бірмәнді сәйкестікті тағайындау негізінде қабылдануымен сипатталады.
Уақыт өте келе адамдар сандарды атауды ғана емес, сонымен қатар оларды белгілеуді де, сондай-ақ олармен амалдар қолдануды да үйренді. «Натурал сан» терминін тұнғыш рет римдік ғалым А. Боэций (шамамен 480-514 жылдар) қолданған. Натурал сан ұғымы қалыптасқаннан кейін сандар дербес объектлерге айналды.
ХІХ ғасырда ғалымдардың назары натурал сандармен есептеулер жұргізуге негіз болған теорияларды құруға және логикалық тұрғыдан негіздеуге аударылды. Натурал сандар ұғымының өте қарапайым және табиғи көрінетіні сондай, ғылымда ұзақ уақыт бойы оны қандай да болсын қарапайым ұғымның терминдерімен анықтау туралы мәселе қойылған жоқ. Бөлшектердің пайда болуы шамаларды өлшеумен пайда болды. Ерте кезде адамдарға сауда - саттық және түрлі есептеу жұмыстарында бөлшектер мен үлестерді есептеу қажет болған. Алғашында математикада бөлшектерді «сынық сандар» деп атаған. Бөлшектер туралы түсініктің дамуында үш түрлі бөлшектер ұғымы қалыптасқан.
- Бірлік бөлшектер - алымдары 1 болатын бөлшектер.
- Жүйеленген бөлшектер. Жүйеленген бөлшектің алымы кез келген бүтін сан, бөлімі тек 10 санының немесе 60 санының дәрежелері ғана болған.
- Жалпы түрдегі бөлшек. Жалпы түрдегі бөлшектің алымы да, бөлімі де кез келген натурал сан болды.
Бөлшектердің мұндай әртүрлілігі есептеу және өлшеу жұмыстарында көптеген қиындықтар туғызды. Бөлшек ұғымының дамуы ғылым мен сауда-саттық жұмыстарында өркендеген елдерде: Мысырда, Вавилонда, Үндістанда және Римде қалыптасты. Ертеде әртүрлі елдер бөлшек сандарды белгілеуде өздерінің түрліше символдарын енгізді. Мысалы, мысырлықтар 1\10-ді -белгісімен, 1\2-ні-- белгісімен және 1\3 -ді -белгісімен көрсеткен. Ежелгі Үндістанда жай бөлшектерді жазуда оның бөлшек сызығын сызбай, алымын үстіне, бөлімін астына жазған. Мысалы, 1\3-ді түріндежазған. Бөлшекті осы түрде жазу тәжік ғалымы әл-Насави (1030 жылдар) ғылыми жұмыстарында орын алған. Ежелден 1\2-ді жарты, 1\4-ді ширек, 1 +1\2-ді бір жарым және т. с. с, деп атаған. Осылайша «жарты», «ширек» ұғымдары қалыптасқан.
1
3
Бөлшек сызығын уал-Хасара және итальяндық Леонардо Пизанский өздерінің жазба есептеулерінде пайдаланған. Леонардо Пизанский «бөлшек» деген сөзді енгізді. Бөлшек сызығы ХҮІ ғасырда ғана белгілеуге толық неді.
Ертедегі вавилондықтар өздерінің ғылыми зерттеулерінде алпыстық бөлшектерді (бөлімі алпыс болатын сан) пайдаланылады. Осыдан қалған бөлшек жүйесінен қазіргі уақыт бірлігіндегі 60-тық жүйе қалыптасқан.
1 мин = 1\60сағ; 1сек = 1\60мин. Бөлшектегі «алым», «бөлім» атауларын ХІІІ ғасырда грек математигі Максим Плаунд енгізген, жалпы түрдегі m\n бөлшегі ежелгі грек ғалымы Архимедтің еңбектерінде пайдаланылған. ХХ ғасырдың алғашқы жылдарында үнділер жай бөлшектерге амалдар қолдануды қалыптастырды.
Самарқанд қаласындағы астрономиялық обсерваторияның негізін салушы әл-каши бөлшек сандарды жазудың барлық түрлендірулер мен есептеулерін айтарлықтай ықшамдайтын түрін, яғни ондық бөлшек деп аталатын жаңа түрін ашты.
ХҮІІ ғасырдың басында ондық бөлшекті жазуды, айыру таңбасы ретінде үтір немесе нүкте қолданыла бастады.
Ондық бөлшектерді есептеу натурал сандарды есептеуге ұқсас және ыңғайлы болғандықтан, ғылымдағы, өндірістегі, күнделікті өмірдегі есептеулерге жиі пайдаланылады. Ондық бөлшектер және ондық бөлшектерге амалдар қолдану туралы ортаазиялық ғалым Әл-Каши өзінің «Арифметика кілті» (1437ж) атты кітабында жазды. Әл-Каши ондық бөлшектерді жазуда үтірді пайдаланбаған, бірақ ол үтірдің орнына тік сызық қойған. Ал, индерландиялық математик Стевин Симон (1548-1620) өзінің ондық бөлшек туралы «Ондық» атты (1585) кітабында үтірді пайдаланбай, бөлшектің бүтін бөлігі мен бөлшек бөлігін бір қатарға үтірсіз жазған. Мысалы, 37, 48 ондық бөлшегін мына түрде жазған: 37 0 4 1 8 2. Үтірдің орнына бірліктің үстіне нөл жазған. 1, 2, 3, . . . цифрларымен ондық таңбалардың ретін белгілеген.
Өмірде, тұрмыста, кездесетін көптегшен шамалар ( жылдамдық, биіктік, температура, баға, т. б. ) көбейіп, азайып өзгеріп отырады. Шамалардың өзгерістерін белгілеу үшін оң сандармен қатар теріс сандар енгізілді. Теріс сандар туралы ең алғашқы ұғым біздің заманымызға дейінгі ІІ ғасырдағы қытай математиктерінің еңбектерінде кездескен. Оң санды «өсу» өзгерісінде қолданса, теріс санды «кему» ретінде қолданған немесе теріс сандар «қарыз» мағынасында қолданса, оң сандарды қолда бар зат «мүлік» деп түсінген.
Кейбір шамалардың тура мағынасы, тура бағыты болумен қатар, қарама- қарсы мағынасы, қарма -қарсы бағыты болады. Шамалардың өзгерісінің сан мәнін жазғанда, оқығанда оның тура мағынасының сан мәнінің алдына «+» таңбасы қойылады. Шаманың қарама-қарсы мағынасының сан мәнінің алдына «-» таңбасы қойылады. Координаталық түзудегі оң (оңға қарай) бағытқа қарама-қарсы (солға қарай) бағыт теріс бағыт деп аталып, ол бағытта теріс сандар кескінделеді. Бір-бірінен тек қана таңбаларымен ажыратылатын сандар қарама-қарсы сандар деп аталады.
Математикаға теріс сандардың енгізілуімен қатар нөл саны да жаңа мағынаға ие болды. Нөл саны санақ басы болып және қарама-қарсы сандардың қосындысы деп есептелді. Үнділер нөлді «сунья» (қазақша «бос» деген мағынаны білдіреді) деп атаған, ал арабтар «ас-сифр» деп аударған, сондықтан ХҮІІ ғасырға дейін нөл «цифр» деп аталып келген .
«Нөл» қазақшаға аударғанда «ешқандай» дегенді білдіретін латынның «nullus» деген сөзінен шыққан.
Қазіргі кездердегі түсінігімізше нөл - сан. Оны басқа сандар сияқты қосуға, азайтуға, көбейтуге, бөлуге болады, тек қана 0-ге санды бөлуге болмайды.
Нөл саны координаталық түзуде санақ басы болатын О нүктесінің координатасы, 0 - саны оң сандар мен теріс сандарды ажыратып тұратын сан, сондықтан 0 саны оң санға да, теріс санға да жатпайды. 0 саны бүтін сандар жиынына жатады.
Қорытындылай келе, натурал сандар жиыны бүтін сандар жиынының ішкі жиыны, бүтін сандар жиыны шектеусіз жиын. Бүтін сандар жиыны, оң және теріс бөлшектер жиыны рационал сандар жиынын құрайды. Мына суретте натурал сандар жиыны бүтін сандар жиынының, ал бүтін сандар жиыны рационал сандар жиынының ішкі жиыны екені Эйлер - Венн дөңгелектері арқылы көрсетілген.
Жалпы, сан ұғымы мұнымен шектеліп қана қоймайды, сандар өте көп әрі шексіз. Рационал сандар жиынына бүтін сандар, оң бөлшек және теріс бөлшек сандар жататыны белгілі. Кез келген рационал санды шектеусіз периодты ондық бөлшекпен жазуға болады. Шектеусіз периодсыз ондық бөлшек түрінде өрнектелген санды иррационал сандар деп атайды. Рационал және иррационал сандар жиындарын нақты сандар жиыны құрайды. Иррационал сандарға және тағы басқа сандар жиынына алдағы уақыттарда толығырақ тоқталып осы баяндаманы әрі қарай жалғастырамыз деген мақсаттамыз.
- Бөлщек түрлеріЖай бөлшек
Жай бөлшек - натурал санның бір немесе бірнеше тең бөліктерінен құралған сан; екі натурал санның қатынасы; ондық бөлшектен өзгеше аталатын арифметикалық бөлшек;
Жай бөлшектерді көбейту
1)
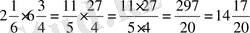
2)
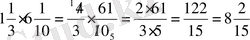
Аралас
сандарды
көбейту
1)
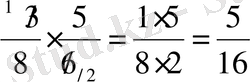
2)
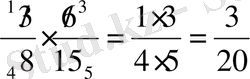
Бөлшекті натурал санға
көбейту
(немесе керісінше)
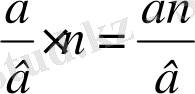 н/е
н/е
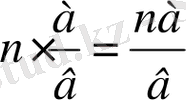
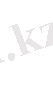
1)
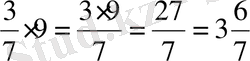
2)
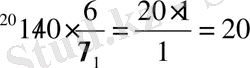
3)
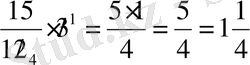
Бөлшектерді
қысқартып
көбейту
Жай бөлшектерді көбейту ережесі
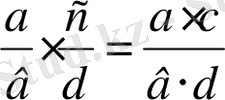 мұнд.
мұнд.
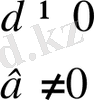
1)
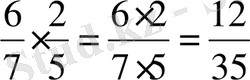
2)
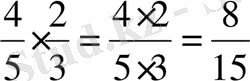
Жай бөлшектерді көбейту
Көбейту амалы :
- Тік төртбұрыштың қабырғалары берілгенде ауданын есептеуде.
- Заттың құнын есептегенде бағасы мен данасы немесе массасы көбейтіледі.
- Жылдамдық пен уақытты көбейтіп, жүрілген жолды есептеуде.
- Тік бұрышты параллепипедтің (м/ы: бөлменің көлемі) көлемін, үш өлшемін ұзындығын, енін, биіктігін көбейтіп есептеуде және т. б. есептер шешуде ондағы шамалар бөлшектермен бірлесе, онда бөлшектерді көбейту амалын білуіміз керек.
Мысалы: Тік төртбұрыш АВСD (плакатта жазылған) ұзындығы
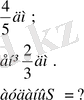
Шешуі: S=ұз. ені
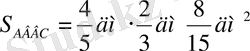
Жауабы:
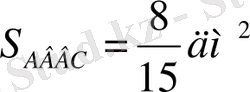
қалай шықты?
Ол үшін қабырғасының ұзындығы 1дм-ге тең шаршы аламыз. Ауданының өлшем бірлігі шаршы бойынша есептелінеді. Ұзындық бойынша шаршыны тең
1 дм.
В
С
дм 2
А 1 дм
D
5 бөлікке, ені бойынша тең 3 бөлікке (бөлшектің бөлімдері бойынша) барлығы тең 15 бөлікке (үлеске) бөлейік. Сонда бір бөліктің ауданы
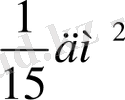
Енді ұзындығынан бөлшектің алымы бойынша 4 бөлікті, енінен бөлшектің алымы бойынша 2 бөлікті бөліп алып, осы бөліктерді бояйық. Сонда ізделенді АВСD тік төртбұрышы шығады. Бұл тік төртбұрышта 8 бөлік боялады. Боялған АВСD тік төртбұрыштың ауданы
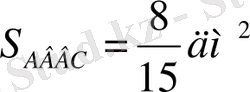
Бұл
жай бөлшегінің алымы көбейтіндісін бөлшектердің алымдарының көбейтіндісі 4·2=8 болса, ал бөлімі олардың бөлімдерінің көбейтінді 5·3=15 екенін көріп тұрмыз.
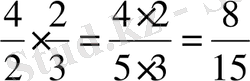
Енді оқушыларға қосымша сұрақтар қойып, оларды жай бөлшектерді көбейту ережесін өздері қорытуға жетелеу керек.
Сұрақтар:
- Шаршы неше бөлікке бөлінеді? (15) .
- Көбейтінді бөлшектің бөлімі қалай табылады? (5·3=15 бөлімдерін көбей-тіп) .
- Тік төртбұрышта неше бөлік бар? (8)
- Көбейтінді бөлшектің алымы қалай табылады? (4·2=8 алымдарын көбей-тіп) .
Осы сұрақтарға жауап беру барысында оқушылар жай бөлшектерді көбейту ережесін өздері тұжырымдап айтады.
Міндетті түрде мұғалімнің өзі ережені оқушыларға ерекше дауыспен айту керек. Сонан соң оның әріппен жазылуын формула
түрінде жазған жөн. Ары қарай тірек конспекті жазылған плакат бойынша түсіндіру.
Жай бөлшектерді көбейткенде бөлшектерді қысқартып, болған соң, көбейту керек. Мысалы:
немесе қысқаша
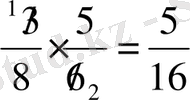
Бөлшекті натурал санға көбейту (немесе керісінше) . Бұл есеп ой қозғауда қарастырылды ғой, сондықтан ережесін оқушылардың өздеріне қорытуға жетелеу керек:
Ереже: Натурал санды бөлшекке көбейткенде натурал сан бөлшектің алымына көбейтіліп, көбейтінді бөлшектің алымы ретінде алынады да, бөлі-мі өзгеріссіз сол қалпында жазылады.
немесе
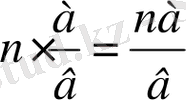
- Ондық Бөлшек
Ондық бөлшек- бөлімі 10 санының бүтін дәрежесі болатын бөлшек (мыс., 1/10=0, 1, 909/1009, 09) . Ондық бөлшек бөлімсіз жазылады, оның бөлімінде қанша нөл болса, алымында оң жағынан сонша сан үтір арқылы ажыратылады. Мысалы, Егер рационал санның бөлімінің жіктеуінде 2 мен 5 сандары қатынасса, ол цифрларының саны шекті Ондық бөлшекке (мыс., ), ал 2 мен 5 сандарынан басқа да жай сан кездессе, бөлшек ақырсыз периодты Ондық бөлшекке айналады. Иррационал сандар шектеусіз периодсыз Ондық бөлшек түрінде көрсетіледі. Барлық жағдайда да акак-1…а0, б1б2… түріндегі Ондық бөлшек мына түрде жазылады: ак10к+ак-110к-1+…+ +а0+ мұндағы ак, ак-1, …, а0, б1, б2, … - санның белгілі бір разрядына сәйкес 0, 1, 2, …, 9 (ак0) сияқты цифр. Ондық бөлшектің жүйесін 1427 ж. Ғийас әд-Дин ибн Масуд Жәмшид әл-Кәши баяндап жазған
Бөлшек сандардың ондық жазылуы
Ондық бөлшектер туралы алғаш рет ХҮ ғасырда ортаазиялық ғалым Әл-Каши ондық бөлшектер, ондық бөлшектерге амалдар қолдануды «Арифметика кілті » деген еңбегінде жазды. Тек натурал сандар көмегімен күнделікті өмірде қажетті өлшеу, зерттеу жұмыстарын жүргізу мүмкін емес, сондықтан ондық бөлшектерді өмірде пайдалану өте қажет, күнделікті тұрмыстада қолданамыз. Әл-Каши еңбектерін одан әрі жалғастырушы нидерландиялық математик Симон Стевин өзінің «Ондық» деген кітабында ондық бөлшектер туралы зерттеулерін жазды. Бөлшек сандар өте қажетті сандар, ол туралы Рим жазушысы Цицерон «Бөлшекті білмейінше математиканы білемін деп ешкім де айта алмайды» десе орыстың ұлы математигі Л. Ф. Магницкий :
Бүтінге келсек жұлынып
Алдына еш жан салмассың
Бөлшекке келсек бұғынып,
Жауабын таба алмассың
Есеп мықты демелік
Бөлшекке көңіл бөлелік.
Ондық бөлшектер дегеніміз бірліктерден де кіші разрядты болатын ондық жүйеде жазылған сан. Ондық бөлшектерді жазғанда бірлік пен ондық үлесің арасына үтір қойылады. Үтірдің алдыңғы бөлігі бүтін бөлік, ал соңындағы бөлік бөлшек бөлік деп аталады.
Ой қозғау: Мына бөлшектер бөлімін 10 келтіріңдер.
Мына бөлшектер бөлімін 100-ге келтіріңдер.
Мына бөлшектер бөлімін 1000-ға келтіріңдер
Осы бөлшектің бүтін бөлігін үтірмен алмастырыңдар, бөлшектің бөліміндегі 10, 100, 1000 сандарды алып тастап, үтірден кейін бөлшектің алымындағы санды жазыңдар. Пайда болған жаңа санды оқуда бөлшек бөліміндегі 10, 100, 1000 сандарды қолданыңдар. 5, 6 3, 21 8, 125 т. с. с.
Ұяшықтардағы сандардың орнын ауыстыра отырып мысалдар берсе оқушылар қызығушылықпен орындайды. Сондай -ақ бүтін және бөлшек бөлігінін разрядтарын шаттаспай айтуга, тез жаттап алуға машықтанады.
Мысалы:
14, 0006, 47, 012 301, 9071
27, 005, 66, 008 65, 527
3, 03, 150, 009 145, 5892
Математикалық диктант:
- интерактивті тақтада сөзбен берілген ондык болшектермен жазу.
-Бөлінділерді жай және ондык бөлшек түрінде жаз
18 :10 = 678 : 1000 = 5687 : 1000 =
5 : 100 = 39 : 100 = 9786 : 100 =
- Ондык бөлшектерді жай бөлшек түрінде жаз.
0, 6 61, 08 100, 5
0, 2 0, 72 11, 3100
2, 03 0, 83 11, 82
Оқулықпен жұмыс: сыныпта, үйде деңгейлік тапсырмалар беру. Қабілетті оқушыларға қосымша есептер беріледі.
Ондық бөлшекті жүйелі түсіндіру, проблеммалық сұрақтар тудыра, бағыт-бағдар, мысалдар бере отырып өз беттерінше меңгерту, алдынғы тақырыптағы ондық бөлшектерге амалдар қолдануды тез ұғып, өз беттерінше есептеуге септігін тигізеді. Өз тәжірибемде өтілген тақырыпты үйде оқып, қажетті ережені «Ереже дәптерге» жазып, өз ойларынан ұқсас мысалдар келтіріп жаттау беріледі және ереже дәптер тұрақты тексеріледі. Білімдерін нактылауда тақырыптық тест алу, жіберілген қатенің мониторингімен жұмыс жүргізу, бұл дегеніміз төменгі сыныптан оқушыларды МАБ-қа, ҰБТ-ге дайындау және білімдерін нақтылау болмақ
Ондық бөлшектерді қосып, азайту натурал сандарды қосып азайту сияқты орындалады. Оларды баған түрінде жазып, разрядтар бойынша қосып азайтамыз.
Ондық бөлшектерді қосу үшін
Ондық бөлшектерді ондық таңбаларының санын нөлдерді тіркеп жазу арқылы теңестіру керек.
Үтірдің астына үтір тура келетіндей етіп, оларды аттас рязрядтар бірінің астына-бірі тұратындай етіп жазу керек
Үтірге көңіл аудармай қосу керек
Шыққан жауапта үтірді берілген бөлшектердегі үтірдің астына келтіріп қою керек
Ондық бөлшектерді азайту үшін
Азайғыш пен азайтқыштағы үтірден кейінгі таңбалардың санын теңестіру керек
Үтірдің астына үтір тура келетіндей етіп, азайғыштың астына азайтқышты жазу керек
Айзайтуды натурал сандарды азайту сияқты орындау керек
Шыққан айырмадағы үтірді азайғыш пен азайтқыштағы үтірдің астына тура келтіріп қою керек
Ондық бөлшектерді қосқанда қосудың ауыстырыдылық, ьерімділік қасиеттері сақталады.
Қосудың қасиеттері
Ауыстырымдылық
Терімділік
a + b = b + a
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz