Жиындар теориясының негіздері: ұғымдар, берілу тәсілдері, амалдар және дәлелдеу әдістері


МАЗМҰНЫ
Кіріспе . . . 2
§1. Жиын ұғымы . . . 4
§2. Жиындардың берілу тәсілдері . . . 10
§3. Жиындарға қолданылатын амалдар . . . 13
§4. Жиындарға байланысты кірістірулер мен теңдіктерді дәлелдеу тәсілдері . . . 22
§5. Сандық жиындар . . . 26
Қорытынды . . . 32
Пайдаланылған әдебиет . . . 34
КІРІСПЕ
Кез келген ғылым саласында «негізгі ұғым» деп аталатын ұғымдар бар. Негізгі ұғымдар негізінде ғылымның сол саласының басқа ұғымдары, тұжырымдары, жалпы теориясы тұрғызылады. Негізгі ұғымдар анықталатын, яғни анықтама берілетін және анықталмайтын, яғни анықтама берілмейтін, тек өзімізге белгілі ұғымдар арқылы түсіндірілетін ұғымдар болып екіге бөлінеді. Мысалы, геометрияның анықтама берілмейтін негізгі ұғымдарына «нүкте», «түзу», «жазықтық» және «арақашықтық» ұғымдары жатады. Жалпы, математиканың кез келген саласы жиындар теориясынан басталуы керек, себебі математиканың кез келген саласы, кез келген бөлімі, кез келген тарауы белгілі бір геометриялық фигуралардың, геометриялық денелердің, теңдеулердің, функциялардың, және т. с. с. математикалық нысандардың жиынын зерттейтіні белгілі. Шынында да, геометрияда геометриялық фигуралардың жиыны, дәлірек айтқанда, планиметрияда жазық фигуралардың жиыны, стереометрияда кеңістіктегі геометриялық денелердің жиыны қарастырылады, алгебрада сандық жиындар қарастырылады, анализ бастамаларында функциялардың жиыны қарастырылады, және т. с. с.
Жиын ұғымы және онымен байланысты басқа да кейбір ұғымдар математиканы алғаш оқытудың негізі болып табылады және онда кеңінен қолданылады. Кейбір оқулықтарда «жиын» термині кездеспейді, бірақ бұл ұғым айқындалмаған түрде қолданылады, ал кейбір оқулықтарда жиын ұғымы символикасымен қоса айқын түрде пайдаланылады. Сан, натурал сандарды қосу және көбейту амалдары және олардың қасиеттері, геометриялық фигура сияқты маңызды ұғымдардың қалыптасуы мектеп математика курсында теориялық-жиындық негізде жүзеге асады.
Жалпы, математиканың кез келген деңгейдегі кез келген саласына арналған оқулықтар мен оқу құралдарында жиындар теориясына тұтас тарау немесе одан кішірек көлемде көңіл бөлінген. Бұл ретте жоғары оқу орындарына арналған әдебиет арасынан /1/-/5/, /9/-/11/, ал мектеп бағдарламасына сәйкес әдебиет арасынан /12/, /15/, /16/-/19/, /21/, /22/ әдебиеттерді атап кетуге болады. Біз жұмысты орындау барысында осы аталған әдебиеттерге баса назар аудардық.
§1. Жиын ұғымы
Жиын ұғымы математиканың негізгі ұғымдарының бірі болып табылады. Негізгі ұғымдарға анықтама берілмейді, олар белгілі ұғымдар арқылы түсіндіріледі. Өзара әртүрлі (бөлек) заттарды қандай да бір қасиеті бойынша біріктіріп, бүтін бір зат ретінде қарастыруға болады. Алынған жаңа зат жиын деп, ал оның құрамындағы заттардың әрқайсысы жиынның элементі деп аталады. «Жиын» сөзі математикада «жиынтық», «жинақ», «класс», «коллекция» деген сөздердің, яғни қайсыбір нәрселер жиынтығын сипаттайтын сөздердің орнына қолданылады, оның үстіне қарастырылып отырған жиынтықта бір ғана нәрсе болуы мүмкін немесе бірде-бір нәрсе болмауы мүмкін.
Мысалдар. Қолымыздағы кітаптың беттерінің жиыны .
Күн жүйесіндегі (системасындағы) планеталар жиыны .
Барлық натурал сандар жиыны .
Координаталық жазықтықтың барлық нүктелерінің
жиыны .
Бұл мысалдардан жиынның элементтерінің саны ақырлы (шектеулі) да, ақырсыз (шектеусіз) да бола алатынын көреміз. Жиынды көбінесе латын алфавитінің үлкен (бас) әріптерімен, ал оның элементтерін кіші әріптермен белгілейді.
Х
жиынының
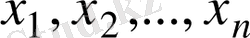 элементтерінен тұратындығы
элементтерінен тұратындығы
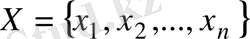 түрінде бейнеленеді.
түрінде бейнеленеді.
Жиын туралы айтқанда кез келген нәрсеге байланысты келесі екі мәселенің біреуі ғана орындалады: не нәрсе бұл берілген жиынға енеді, не нәрсе бұл берілген жиынға енбейді.
х
заты
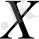 жиынының элементі болатыны
жиынының элементі болатыны
 символымен белгіленеді («
х
символымен белгіленеді («
х
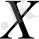 жиынына тиісті», «
х
жиынына тиісті», «
х
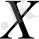 жиынының элементі» деп оқылады) .
жиынының элементі» деп оқылады) .
х
заты
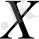 жиынының элементі болмайтыны
жиынының элементі болмайтыны
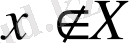 символымен
символымен
белгіленеді (« х Х жиынына тиісті емес», « х Х жиынының элементі емес»
деп оқылады) .
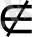 символының орнына
символының орнына
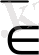 символы да қолданылады.
символы да қолданылады.
Мысал.
Егер
 арқылы натурал сандар жиынын белгілесек, онда
арқылы натурал сандар жиынын белгілесек, онда
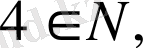
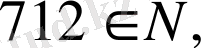
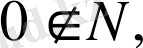

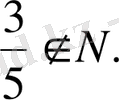
Жиынның өзі ешқашан өзінің элементі болмайды:
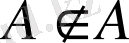 .
.
Жалпылама үшін және тұжырымдамалардың қарапайымдылығы мен қолдануға ыңғайлылығы үшін «құр жиын» ұғымын енгізген жөн.
Бірде-бір элементі жоқ жиынды бос ( құр ) жиын деп атайды да, Ø символымен белгілейді.
Мысалы,
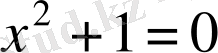 теңдеуінің нақты түбірлері жиыны құр жиын болады.
теңдеуінің нақты түбірлері жиыны құр жиын болады.
Құр жиынмен қатар «бір элементті» жиындарды, яғни бір ғана элементі бар жиындарды қарастыруға тура келеді. Мысалы,
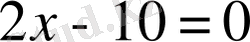 теңдеуінің түбірлерінің жиыны бір элементтен, 5 санынан ғана тұрады. Бір элементті жиынды оның жалғыз элементімен шатастырмау керек.
теңдеуінің түбірлерінің жиыны бір элементтен, 5 санынан ғана тұрады. Бір элементті жиынды оның жалғыз элементімен шатастырмау керек.
Егер
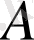 жиынының элементтерінің жалпы атауы
жиынының элементтерінің жалпы атауы
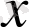 болса, онда кейде былайша жазады:
болса, онда кейде былайша жазады:
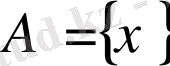 .
.
Анықтама. А және В жиындары берілген болсын. Егер А жиынының әрбір элементі В жиынының да элементі болса, онда А жиыны В жиынының ішкі жиыны ( жиыншасы ) деп аталып, былайша белгіленеді:
 немесе
немесе
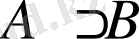 .
.
Мұндай қатынас енгізу ( ену ) деп аталады.
Айталық, А - колледждегі барлық студенттер жиыны, ал В - осы колледждегі бір топтың студенттерінің жиыны болсын. Әрине, В жиыны А жиынының бір бөлігі, немесе, басқаша айтқанда, В жиыны А жиынына кіреді. Сонымен, анықтамаға сәйкес В жиыны А жиынының ішкі жиыны.
Егер
 және
және
 болса, онда
болса, онда
 екендігіне көз жеткізу қиын емес. Шынында да,
А
жиынының әрбір элементі
В
жиынына, ал өз кезегінде
В
жиынының әрбір элементі
С
жиынына тиісті. Ендеше,
А
жиынының әрбір элементі
С
жиынына да тиісті, яғни
екендігіне көз жеткізу қиын емес. Шынында да,
А
жиынының әрбір элементі
В
жиынына, ал өз кезегінде
В
жиынының әрбір элементі
С
жиынына тиісті. Ендеше,
А
жиынының әрбір элементі
С
жиынына да тиісті, яғни
 . Бұл жағдайды Эйлер-Венн диаграммасы арқылы былай кескіндеуге болады (Эйлер-Венн диаграммасы туралы үшінші параграфта толығырақ айтатын боламыз) :
. Бұл жағдайды Эйлер-Венн диаграммасы арқылы былай кескіндеуге болады (Эйлер-Венн диаграммасы туралы үшінші параграфта толығырақ айтатын боламыз) :
B
A
С
Ұғымдар мен нәрселер жиынтықтарының әр түрлі бөліктерін қарастырғанда біз әрдайым ішкі жиын ұғымын қолданып отырамыз. Ана тіліміздегі сөйлемдегі барлық сөздер жиынының әр түрлі ішкі жиындарын - зат есімдерді, сын есімдерді, етістіктерді, т. с. с. қарастырамыз. География және тарих сабақтарында барлық елдер, барлық қалалар, барлық көлдер, т. с. с. жиындардың әр түрлі ішкі жиындарын оқимыз. Осы сияқты күнделікті өмірде де ішкі жиын ұғымын пайдаланамыз. Мысалы, қайсыбір елді мекендегі бір көше бойындағы үйлер сол елді мекендегі барлық үйлер жиынтығының ішкі жиыны болады; жатақханадағы бір қабатта орналасқан бөлмелер жиынтығы сол жатақханадағы барлық бөлмелер жиынының ішкі жиыны болады, бөлмедегі орындықтар жиыны сол бөлмедегі барлық жиһаздар жиынының ішкі жиыны болып табылады және т. с. с.
Ішкі жиын ұғымы математикада да кеңінен қолданылады. «Берілген сөйлемдегі барлық зат есімдердің астын сызыңдар», «1-ден 10-ға дейінгі сандардың ішінен 2-ге бөлінетін сандарды атаңдар», «Берілген сандардың арасынан үш таңбалы сандарды атаңдар», «Әр түрлі фигуралардың ішінен үшбұрыштарды көрсетіңдер», «Туған өлкемізде кездесетін құстарды атаңдар» деген тапсырмаларды орындату арқылы ана тілі сабағында да, табиғаттану сабағында да, математика сабағында да төменгі сынып оқушыларын жиынның бөліктерін ажырата білуге үйретеміз.
Жиын және ішкі жиын ұғымдарын меңгергеннен кейін, біздің енді геометриялық ұғымдарды дәлірек анықтауымызға болады. Геометриядағы ең маңызды ұғымдардың бірі фигура ұғымы «нүкте» және «жиын» ұғымдары арқылы анықталады. Геометриялық фигура деп нүктелердің кез келген құр емес жиынын атайды. Олай болса, жеке алынған нүкте де, нүктелердің шектеулі жиыны да геометриялық фигура болып табылады. Кесінді, түзу, сәуле, үшбұрыш, шеңбер, дөңгелек, доға және де басқа нүктелердің шектеусіз жиындары геометриялық фигуралар болып табылады.
Егер
 нүктесі
нүктесі
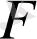 фигурасына тиісті болса, онда жиындар теориясында, жалпы математика курсында қолданылатын және жоғарыда айтылған ережелерге сәйкес
фигурасына тиісті болса, онда жиындар теориясында, жалпы математика курсында қолданылатын және жоғарыда айтылған ережелерге сәйкес
 түрінде жазады; егер
түрінде жазады; егер
 нүктесі
нүктесі
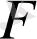 фигурасына тиісті емес болса, онда
фигурасына тиісті емес болса, онда
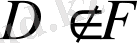 түрінде жазады.
түрінде жазады.
F
. D
T .
Мысалы,
 натурал сандар жиыны,
натурал сандар жиыны,
 бүтін сандар жиыны,
бүтін сандар жиыны,
 рационал сандар жиыны,
рационал сандар жиыны,
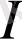 иррационал сандар жиыны,
иррационал сандар жиыны,
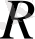 нақты сандар жиыны,
нақты сандар жиыны,
 комплекс сандар жиыны болса, онда
комплекс сандар жиыны болса, онда
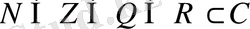 ,
,
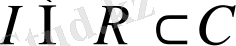 .
.
Кез келген жиын өзінің ішкі жиыны болып табылады:
 .
.
Құр жиын кез келген
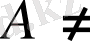 Ø
жиынының ішкі жиыны болады деп есептеледі:
Ø
жиынының ішкі жиыны болады деп есептеледі:
Ø
 .
.
А жиынының құр емес В ішкі жиыны А жиынымен дәлме-дәл келмейтін болса, онда оны меншікті ішкі жиын деп атайды. А жиынының А және Ø ішкі жиындарын оның меншікті емес ішкі жиындары деп атайды.
Мысалы,
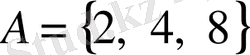 жиынының алты меншікті ішкі жиыны бар:
жиынының алты меншікті ішкі жиыны бар:
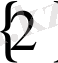 ,
,
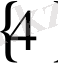 ,
,
 ,
,
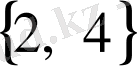 ,
,
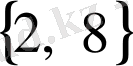 ,
,
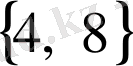 ; екі меншікті емес ішкі жиыны бар:
; екі меншікті емес ішкі жиыны бар:
 және
Ø
.
және
Ø
.
Егер А жиынының элементтерінің саны n болса, онда оның ішкі жиындарының саны 2 n болады.
А жиынының барлық ішкі жиындарының жиынын
А
жиынының булеаны деп атайды. Белгілеуі
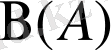 . Сонда
. Сонда
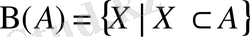 .
.
Анықтама.
Егер
А
және
В
жиындары үшін
 және
және
 кірістірулері бірдей орындалса, яғни бірінің кез келген элементі екіншісіне де тиісті болса, онда
А
және
В
жиындары
тең
дейді де,
А
=
В
символымен белгілейді.
кірістірулері бірдей орындалса, яғни бірінің кез келген элементі екіншісіне де тиісті болса, онда
А
және
В
жиындары
тең
дейді де,
А
=
В
символымен белгілейді.
Мысалы, егер
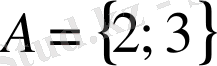 және
В
жиыны
және
В
жиыны
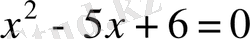 теңдеуінің түбірлерінің жиыны болса, онда
А
=
В
.
теңдеуінің түбірлерінің жиыны болса, онда
А
=
В
.
Басқаша айтқанда, егер
А
және
В
екі жиын бірдей элементтерден тұратын болса, онда оларды тең жиындар деп атайды және
А
=
В
деп жазады. Мысалы,
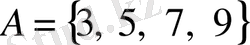 және
және
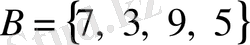 жиындары өзара тең, өйткені бірдей элементтерден тұрады. Элементтерінің орындарын ауыстырғаннан жиын өзгермейді.
жиындары өзара тең, өйткені бірдей элементтерден тұрады. Элементтерінің орындарын ауыстырғаннан жиын өзгермейді.
§2. Жиындардың берілу тәсілдері
Егер әрбір нәрсе туралы оның жиынға тиісті немесе тиісті емес екендігін айта алатын болсақ, онда жиын берілген деп саналады.
Жиынды оның
барлық элементтерін
атау арқылы анықтап беруге болады. Егер
 ,
,
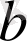 ,
,
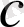 ,
,
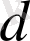 - әртүрлі нәрселердің белгілеулері болса, онда осы нәрселердің жиынын
- әртүрлі нәрселердің белгілеулері болса, онда осы нәрселердің жиынын
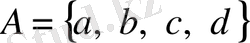
түрінде жазып, оны « А жиыны a , b , c , d элементтерінен тұрады» деп оқиды.
Әрбір нәрсе жиынға тек бір рет қана енеді. Мысалы, 62 545 772 санының әртүрлі цифрларынан тұратын жиын
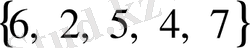 , ал «есеп» деген сөздегі әртүрлі әріптер жиыны
, ал «есеп» деген сөздегі әртүрлі әріптер жиыны
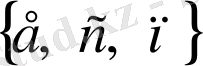 түрінде жазылады.
түрінде жазылады.
Жиынның берілуінің осы тәсілі математикада жиі қолданылады. Мысалы, радиусы R , центрі О нүктесі болатын шеңбердің «центрі О нүктесі, радиусы R болатын шеңбер деп жазықтықтың О нүктесінен R қашықтықта жататын барлық нүктелерінің жиыны» деген анықтамасын еске түсірейік. О нүктесінен R қашықтықта және О нүктесімен бір жазықтықта жату - центрі О нүктесі, радиусы R болатын шеңбердің барлық нүктелеріне тән қасиет және бұл қасиетке шеңберге тиісті емес бірде-бір нүкте ие бола алмайды.
Жиынның берілуінің тағы бір тәсілі оны құрайтын нәрселердің ортақ қасиетін атау болып табылады. Мұндай қасиетті сипаттамалық қасиет деп атайды.
Элементтердің сипаттамалық қасиеті көрсетілген жиынды былай жазуға болады: фигуралық жақшалар ішіне алдымен элементтердің белгіленуін жазады. Содан кейін не вертикаль сызықша, не қос нүкте қояды да, одан кейін осы жиын элементтеріне және тек соларға тән қасиетті жазады. Мысалы, 6-дан кіші натурал сандардың А жиынын қарастырайық. Бұл жиынды былайша жаза аламыз:
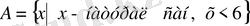
немесе
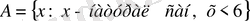 .
.
Егер
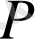 арқылы белгілі бір қасиетті белгілесек, онда осы қасиетті қабылдайтын нәрселердің барлығынан құрылған жиын
арқылы белгілі бір қасиетті белгілесек, онда осы қасиетті қабылдайтын нәрселердің барлығынан құрылған жиын

символымен белгіленеді.
Егер
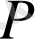 қасиетін бірде-бір нәрсе қабылдамаса, онда
қасиетін бірде-бір нәрсе қабылдамаса, онда
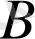 жиыны құр жиын болады.
жиыны құр жиын болады.
Мысалы,
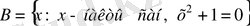
 Ø
(мұнда
Р
қасиеті ретінде
х
заты нақты сан болып, оның квадраты мен 1 санының қосындысы нөлге тең болуы алынған) .
Ø
(мұнда
Р
қасиеті ретінде
х
заты нақты сан болып, оның квадраты мен 1 санының қосындысы нөлге тең болуы алынған) .
Мысалы, 6-дан кіші натурал сандардың
А
жиынын қарастырайық. Бұл жерде
А
жиынының барлық элементтеріне ортақ қасиет, атап айтқанда, олардың «натурал және 6-дан кіші сан болуы» аталып отыр. Қарастырылып отырған
А
жиынының барлық элементтерін атап шығу қиындыққа түспейді:
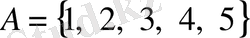 .
.
Жиын элементтерінің өздері де жиын болуы мүмкін. Мысалы, колледждегі топтардың (группалардың) жиыны туралы айтуға болады. Бұл жиынның элементтері - топтар, ал топтың өзі сол топтағы студенттер жиыны болады. Бірақ студенттер колледждегі топтар жиынының элементтері бола алмайды.
Сонымен, қандай да бір жиын берілген болуы үшін не оның элементтерін атап шығу, не оның элементтеріне тән қасиетті көрсету қажет. Екінші тәсіл бірінші тәсілге қарағанда жалпылау екенін айта кетеміз. Мәселе мынада: жиынның элементтерін атап шығу осы жиын шектеулі болғанда ғана мүмкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болғанда да, шектеусіз болғанда да көрсетуге болады.
Бірақ кейбір кезде шектеусіз жиынды да бірінші тәсілді пайдаланып жазып көрсетуге болады. Мысалы, барлық натурал сандар жиынын

арқылы белгілеп, мына түрде жазуға болады:
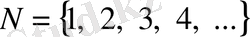 .
.
Әрине, жиынды тек көп нүктелер орнында не болатыны белгілі жағдайда ғана осы түрде жазуға болады.
Барлық натурал сандардан және нөлден тұратын жиынды
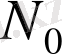 арқылы белгілеп, былайша жазады:
арқылы белгілеп, былайша жазады:
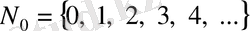 .
.
Бұл жиынды теріс емес бүтін сандар жиыны деп атайды.
Теріс бүтін сандардың жиынын
 арқылы белгілеп, былай жазуға болады:
арқылы белгілеп, былай жазуға болады:
 .
.
Барлық бүтін сандар жиынын, яғни барлық натурал сандардан, барлық теріс бүтін сандардан және нөлден тұратын жиынды
 арқылы белгілеп, былай жазады:
арқылы белгілеп, былай жазады:
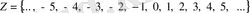 .
.
§3. Жиындарға қолданылатын амалдар
Енді жиындарға қолданылатын кейбір амалдарды анықтайық.
1. Жиындардың бірігуі. Екі жиынның бірігуі.
Анықтама.
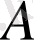 және
және
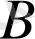 жиындарының ең болмағанда біреуіне тиісті элементтерден, тек сол элементтерден ғана тұратын жиынды
жиындарының ең болмағанда біреуіне тиісті элементтерден, тек сол элементтерден ғана тұратын жиынды
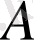 және
және
 жиындарының
бірігуі
деп атайды да,
символымен белгілейді.
жиындарының
бірігуі
деп атайды да,
символымен белгілейді.
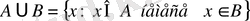 .
.
Жиындарға қолданылатын амалдарды түсіндіруді жеңілдету үшін жиындардың жазықтықтағы кескіндері болатын Эйлер-Венн диаграммалары деп аталатын геометриялық кескіндерін қолданады. Екі жиынның бірігуін Эйлер-Венн диаграммасы арқылы былайша кескіндеуге болады. А мен В жиындарын дөңгелектер арқылы белгілесек, олардың бірігуі боялған облыс болады. А мен В жиындарының ортақ элементтері жоқ болса, яғни олар қиылыспайтын болса, онда да бұл екі жиынның бірігуі анықталады.
A
B
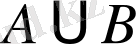
A
B
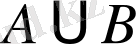
Жоғарыдағы тәсілмен үш және одан да көп жиындардың бірігуін анықтауға болады. Мысалы,
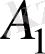 ,
,
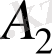 ,
,
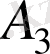 , . . . ,
, . . . ,
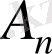 n
жиынның бірігуі
n
жиынның бірігуі

A
B

С
немесе
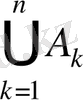
арқылы белгіленеді.
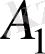 ,
,
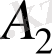 ,
,
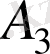 , . . . ,
, . . . ,
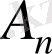 , . . . жиындар тізбегінің бірігуі
, . . . жиындар тізбегінің бірігуі
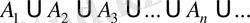
немесе
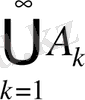
арқылы белгіленеді.
Мысалы,
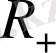 барлық оң сандардың жиыны болса, онда
барлық оң сандардың жиыны болса, онда
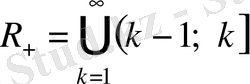 .
.
Егер
 болса, онда
болса, онда
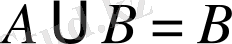
болатыны түсінікті, бұдан дербес жағдайда
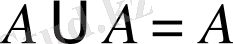 .
.
2. Жиындардың қиылысуы. Екі жиынның қиылысуы.
Анықтама.
А
және
В
жиындарының екеуіне де тиісті элементтерден тұратын жиынды
А
және
В
жиындарының
қиылысуы
деп атайды да,
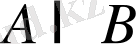 символымен белгілейді.
символымен белгілейді.
A
B
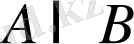
 .
.
Екі жиынның қиылысуын Эйлер-Венн диаграммасы арқылы былайша кескіндеуге болады. А мен В жиындарын дөңгелектер арқылы белгілесек, олардың қиылысуы боялған облыс болады. А мен В жиындарының ортақ элементтері жоқ болса, яғни олар қиылыспайтын болса, онда да бұл екі жиынның қиылысуы анықталады, және ол құр жиын болады.
Егер
А
және
В
жиындарының бір де бір ортақ элементі болмаса, яғни бұл екі жиын қиылыспайтын болса, онда
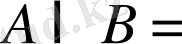 Ø.
Бұл жағдайда
А
және
В
жиындары
қиылыспайды
деп те атайды.
Ø.
Бұл жағдайда
А
және
В
жиындары
қиылыспайды
деп те атайды.
A
B
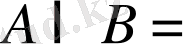 Ø
Ø
Жоғарыдағы тәсілмен үш және одан да көп жиындардың қиылысуын анықтауға болады. Мысалы,
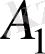 ,
,
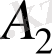 ,
,
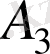 , . . . ,
, . . . ,
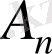 n
жиынның қиылысуы
n
жиынның қиылысуы
A
B
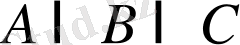
С
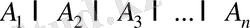
немесе

арқылы белгіленеді.
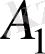 ,
,
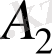 ,
,
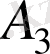 , . . . ,
, . . . ,
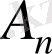 , . . . жиындар тізбегінің қиылысуы
, . . . жиындар тізбегінің қиылысуы

немесе
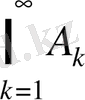
арқылы белгіленеді.
Мысалы,
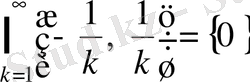 ,
,
яғни бір элементті жиын, ал
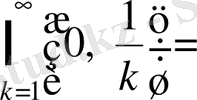 Ø
,
Ø
,
яғни құр жиын.
Егер
 болса, онда
болса, онда
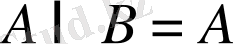
болатыны түсінікті, бұдан дербес жағдайда
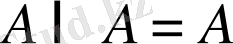 .
.
3. Екі жиынның айырмасы.
Анықтама.
А
жиынына тиісті, ал
В
жиынына тиісті емес элементтерден тұратын жиынды
А
және
В
жиындарының
айырмасы
деп атайды да,
 символымен белгілейді.
символымен белгілейді.
А
және
В
жиындарының айырмасын
 символымен қатар A\B символымен де белгілейді.
символымен қатар A\B символымен де белгілейді.
A
B
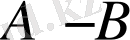
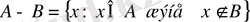
немесе
A\B=
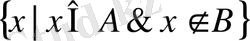 .
.
А
және
В
жиындарының айырмасын қарастырғанда бұл жиындардың реттелген болуы маңызды екенін атап кетеміз.
В
-
А
және
В
-
А
жалпы жағдайда екі түрлі нәрселер. Себебі,
A
B
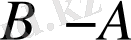
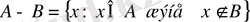 болса,
болса,
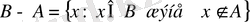 , яғни
, яғни
 және
және
 екеуі екі түрлі жиындар екендігі көрініп тұр.
екеуі екі түрлі жиындар екендігі көрініп тұр.
Мысалы, егер
 және
және
 болса, онда
болса, онда
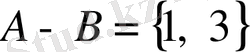
және
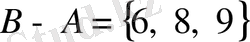 .
.
Әрине, егер
 және
және
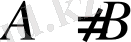 болса, онда
болса, онда
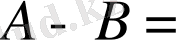 Ø.
Ø.
1-теорема.
 .
.
2-теорема.
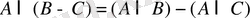 .
.
Екі жиынның айырмасы кез келген жағдайда анықталған. Екі жиын қиылысатын болса, онда олардың айырмасы анықтамаға сай, бірінші жиынға тиісті, ал екінші жиынға тиісті емес элементтерден тұратын жиын екені түсінікті. Яғни бұл жағдайда бірінші жиыннан екі жиынға ортақ элементтерді алып тастағанда осы екі жиынның осы реттегі айырмасы шығады. Ал егер екі жиын қиылыспайтын болса, яғни
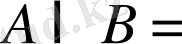 Ø
болса, онда
Ø
болса, онда
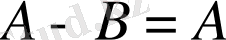 және
және
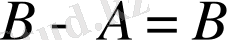 . Бұл екі жағдай төмендегі Эйлер-Венн диаграммаларында сәйкесінше бейнеленген.
. Бұл екі жағдай төмендегі Эйлер-Венн диаграммаларында сәйкесінше бейнеленген.
A
B
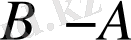
A
B
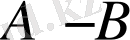
Егер
 және
және
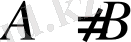 болса, онда
болса, онда
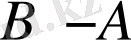 анықталған және бұл айырма келесі пунктте анықталатын толықтауыш жиын болады.
анықталған және бұл айырма келесі пунктте анықталатын толықтауыш жиын болады.
B

A
4. Әмбебап жиын. Қандай жиын қарастырсақ та, оның басқа бір үлкен жиынның ішкі жиыны болатынын көруге болады. Мысалы, топ студенттерінің жиыны курс студенттерінің жиынының ішкі жиыны, ал соңғысы университет студенттерінің жиынының ішкі жиыны т. с. с. Бұл мысалдан үлкен жиын ұғымы өзгеріп отыратынын түсінуге болады.
Жиындар теориясында жеткілікті дәрежеде ауқымды жиынды алып, оның көлемінен шығып кетпейтіндей бекітілген жиынды алып қарастырады да, ол жиынды
әмбебап
(
универсал
)
жиын
деп атайды. Қарастырылатын жиындардың барлығының барлық элементтері осы әмбебап жиынға тиісті деп есептеледі, яғни қарастырылатын жиындардың барлығы да осы әмбебап жиынның ішкі жиындары болады. Әмбебап жиынды
 (орыстың «универсальный» («әмбебап») деген сөзінің бірінші әрпі) символымен белгілеу келісілген.
(орыстың «универсальный» («әмбебап») деген сөзінің бірінші әрпі) символымен белгілеу келісілген.
Кез келген жиынды графикалық түрде кескіндеуге болады. Ол үшін тұйық контур сызамыз да, жиынның элементтері осы контурдың ішіндегі нүктелермен кескінделген деп түсінеміз. Суретте нүктелерді жекелеп көрсету міндетті емес. Универсал жиын тіктөртбұрыш түрінде, оның ішкі жиындары осы тіктөртбұрышта жататын тұйық контур ретінде кескінделеді. Жиындарды бұл түрде кескіндеу Эйлер-Венн диаграммалары деп аталады.
Көп жағдайда сыртқы төртбұрышты сызбайды, универсал жиынды атап көрсетпейді.
5. Толықтауыш жиын.
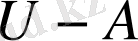 жиыны
жиыны
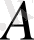 жиынының
жиынының
 әмбебап жиынына дейінгі
толықтауыш жиыны
(
толықтауышы
) деп аталады және
әмбебап жиынына дейінгі
толықтауыш жиыны
(
толықтауышы
) деп аталады және
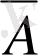 символымен белгіленеді, яғни
символымен белгіленеді, яғни
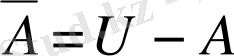 .
.
Сонда, егер
 болса, онда
болса, онда
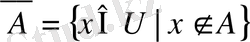 .
.
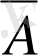
А
Мысалы,
 әмбебап жиыны ретінде нақты сандар жиыны
әмбебап жиыны ретінде нақты сандар жиыны
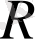 , ал оның ішкі жиыны ретінде рационал сандар жиыны
, ал оның ішкі жиыны ретінде рационал сандар жиыны
 алынса, онда
алынса, онда
 -дің толықтауыш жиыны
-дің толықтауыш жиыны
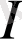 иррационал сандар жиыны болады, яғни
иррационал сандар жиыны болады, яғни
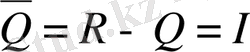 .
.
6. Жиындар теориясының негізгі 19 теңдігі.
1º.
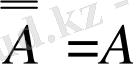 .
.
2º.
 .
.
3º.
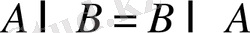 .
.
4º.
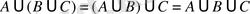 .
.
5º.
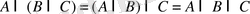 .
.
6º.
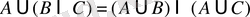 .
.
7º.
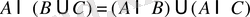 .
.
8º.
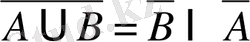 .
.
9º.
 .
.
10º.
 .
.
11º.
 .
.
12º.
 .
.
13º.
 Ø
Ø
 Ø
.
Ø
.
14º.
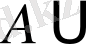 Ø
Ø
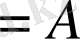 .
.
15º.
 .
.
16º.
 .
.
17º.
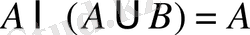 .
.
18º.
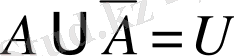 .
.
19º.
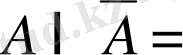 Ø
.
Ø
.
1º-қасиет
екі рет толықтау заңы
, 2º мен 3º-қасиеттер
коммутативтік
(орын ауыстыру)
заңдары
, 4º пен 5º-қасиеттер
ассоциативтік
(терімділік)
заңдары
, 6º мен 7º-қасиеттер
дистрибутивтік
(үлестірімділік)
заңдары
, 8º бен 9º-қасиеттер
Де Морган заңдары
, 12º-15º-қасиеттер
құр жиын мен әмбебап жиын
(
Ø
мен
 )
заңдары
, 16º мен 17º-қасиеттер
жұтылу заңдары
деп аталады.
)
заңдары
, 16º мен 17º-қасиеттер
жұтылу заңдары
деп аталады.
Бұл он тоғыз қасиеттің әрқайсысының алатын орны бар және оларды дәлелдеу қиынға соқпайды.
7. Екі жиынның симметриялық айырмасы.
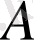 және
және
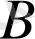 жиындарының
симметриялық айырмасы
деп
жиындарының
симметриялық айырмасы
деп
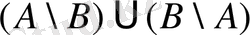 ережесімен анықталатын жиынды атап, оны
ережесімен анықталатын жиынды атап, оны
 символымен белгілейді, яғни
символымен белгілейді, яғни
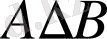
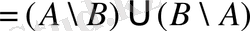 .
.
Келесі теңдіктер орындалады:
A
B
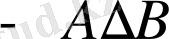
U
1.
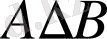
 .
.
2.
 -
-
коммутативтік.
3.
 .
.
4.
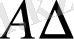 Ø
Ø
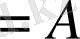 .
.
§4. Жиындарға байланысты кірістірулер мен теңдіктерді дәлелдеу тәсілдері
Жиындарға байланысты кірістірулер мен теңдіктерді дәлелдеудің негізгі екі тәсілі бар. Олардың біріншісі - анықтамалар мен дәлелденген теңдіктер және қатыстарды қолдану тәсілі, екіншісі - Эйлер-Венн диаграммаларын амалдардың негізгі қасиеттерімен қоса пайдалана отырып дәлелдеу қажет болатын өрнектің екі жағын параллель түрлендіру тәсілі. Осы екі тәсілдің қолданылуларын бір нақты мысалмен түсіндіреміз.

 теңдігін дәлелдейік.
теңдігін дәлелдейік.
1-тәсіл - анықтамалар мен дәлелденген теңдіктер және қатыстарды қолдану тәсілі.
 болсын. Онда екі жиынның айырмасының анықтамасына сәйкес
болсын. Онда екі жиынның айырмасының анықтамасына сәйкес
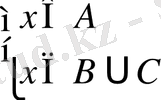 .
.
Бұдан
 , және
, және
 .
.
Әрі қарай
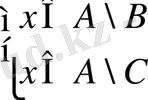 және
және
 ; яғни теңдіктің сол жағындағы жиынының әрбір элементі теңдік таңбасының оң жағындағы жиынға тиісті екендігі, яғни
; яғни теңдіктің сол жағындағы жиынының әрбір элементі теңдік таңбасының оң жағындағы жиынға тиісті екендігі, яғни

 кірістіруі дәлелденді.
кірістіруі дәлелденді.
Енді
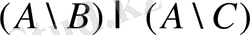
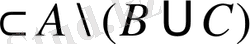 кірістіруін дәлелдейік. Ол үшін
кірістіруін дәлелдейік. Ол үшін
 элементін аламыз. Екі жиынның қиылысуының анықтамасынан
элементін аламыз. Екі жиынның қиылысуының анықтамасынан
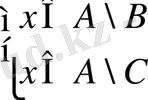 екендігі шығады. Соңғы қатынастардан екі жиынның айырмасының анықтамасы бойынша келесі қатынастар алынады:
екендігі шығады. Соңғы қатынастардан екі жиынның айырмасының анықтамасы бойынша келесі қатынастар алынады:
 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz