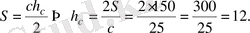Мектеп бітірушілерге арналған математикадан кешенді тест тапсырмалар жинағы: 5 нұсқа, 125 есептің толық шешуі мен талдауы


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 58 бет
Таңдаулыға:
МАЗМҰНЫ
Кіріспе . . . 3
1-нұсқа . . . 5
2-нұсқа . . . 22
3-нұсқа . . . 39
4-нұсқа . . . 53
5-нұсқа . . . 69
Қолданылған әдебиеттер тізімі . . . 86
Кіріспе
Қымбатты мектеп бітіруші жас дос!
Сені алда үлкен жауапкершілікті талап ететін мектеп бітіру және жоғары оқу орнына қабылдау емтиханы күтіп тұр. Мұндай үлкен де жауапты сынақтан ойдағыдай өту үшін жеткілікті дәрежедегі дайындық қажет.
1999 жылдан бастап еліміздің жоғары оқу орындарына қабылдау Қазақстан Республикасы Білім және ғылым министрлігінің Білім беру мен тестілеудің мемлекеттік стандарттарының ұлттық орталығы (БТМСҰО) өткізетін кешенді тест сынағы түрінде жүргізілуде. Шығармашылық емтихандары бар мамандықтардан басқа мамандықтарды қалаған талапкерлер қабылдау емтиханында міндетті үшінші пән ретінде математикадан тестілік тапсырма орындайтыны баршаға аян. БТМСҰО жыл сайын (1999-2014 жылдар) жоғары оқу орындарына түсуге тілек білдіруші талапкерлерге арнап әдістемелік құрал (тестілік тапсырмалар жинағы) дайындап, ұсынып отырғаны белгілі. 2001-жылдан бастап жыл сайын шыққан жинақтарда есептер нұсқаларға (варианттарға) бөлініп, әр жылғы жинақ 20-35 нұсқадан тұратын құрал түрінде шығарылды.
Біз бұл еңбекте БТМСҰО бекіткен тест бағдарламасына енетін базалық тест тапсырмасы жинағына сәйкес құрастырылған 5 нұсқаны толық шешуімен беріп отырмыз, яғни 125 есеп егжей-тегжейлі талданып, геометрия есептері көрнекі сызбалармен сүйемелдей отырып шешілген. Мұндай толық талдаулар сіздерге өз беттеріңізше есептер шешу барысында көп көмегін тигізеді деген ойдамыз. Сонымен қатар, еңбектің соңында осы жұмысты орындау барысында автор қолданған және жас математик-ұстаздар мен оқушыларға танысуға ұсынылатын әдебиеттер тізімі келтірілген.
Бұл еңбекке еніп отырған материалдар 2009-2015 жылдар аралығында Батыс Қазақстан облысының Қаратөбе мектеп-гимназиясында, 2011-2014 оқу жылдар аралығында еліміздің алдыңғы қатарлы мектептерінің бірі болып табылатын Батыс Қазақстан облысы Теректі аудандық «Үміт» лингвистикалық гимназиясында толығымен талданды. Оқу-әдістемелік құралы мектеп мұғалімдеріне де оқу процесінде көмекші құрал ретінде көмегін тигізуі мүмкін.
ІСКЕ СӘТ!
1-нұсқа
1.
Өрнектің мәнін табыңыз:
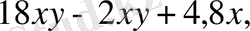 мұндағы
мұндағы
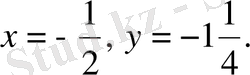
А) 12, 4 .
B)
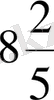 .
.
C) -12, 4 .
D)
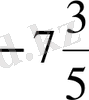 .
.
E) 7, 6 .
Шешуі.
Ұқсас мүшелерін біріктіріп,
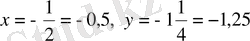 екенін ескерсек,
екенін ескерсек,
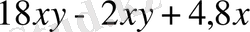 =16
xy
+ 4, 8
x
=
=16
xy
+ 4, 8
x
=
=16 ∙ (-0, 5) ∙ (-1, 25) + 4, 8 ∙ (-0, 5) = 10-2, 4 = 7, 6.
Жауабы. 7, 6. E) .
2. Сағатына 70 км/сағ жол жүретін жүрдек поезд С станциясынан D станциясына қарай шықты, ал 1 сағат өткеннен кейін оған қарама-қарсы D станциясынан сағатына 45 км/сағ жол жүретін жүк поезы шықты. Егер CD темір жол бөлігінің ұзындығы 530 км болса, онда осы екі поезд бірімен-бірі D станциясынан қандай қашықтықта кездесер еді?
А) 220 км.
B) 190 км.
C) 180 км.
D) 200 км.
E) 210 км.
Шешуі. 1-ші сағатта жүрдек поезд 70 км жүреді, қалған 530 - 70 = 460 км жолды екі поезд жүріп өтеді. Екі поезд А нүктесінде кездеседі делік және DA = x болсын. Есеп шарттарына сәйкес теңдіу құрып, оны шешеміз:
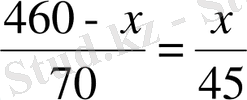 ,
,
 ,
,
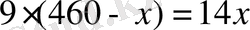 ,
,
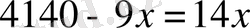 ,
,
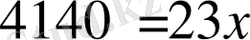 ,
,
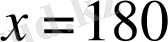 км. Яғни, жүк поезы кездескенге дейін 180 км жол жүреді.
км. Яғни, жүк поезы кездескенге дейін 180 км жол жүреді.
х
C
D
70 км
А
460- х км
Жауабы. 180 км. С) .
3.
Түбірлері бойынша квадрат теңдеу құрыңыз:
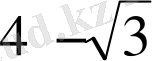 және
және
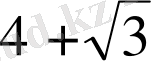 .
.
А) x 2 - 8x + 13 = 0.
B) -x 2 - 8x + 13 = 0.
C) x 2 - 8x - 13 = 0.
D) x 2 + 8x + 13 = 0.
E) x 2 + 16x + 12 = 0.
Шешуі.
Келтірілген
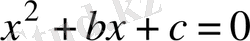 квадраттық теңдеуі үшін Виет теоремасын қолданамыз:
квадраттық теңдеуі үшін Виет теоремасын қолданамыз:
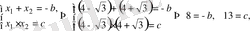 яғни
яғни
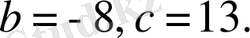 Белгісіздердің табылған мәндерін орындарына қоямыз:
Белгісіздердің табылған мәндерін орындарына қоямыз:
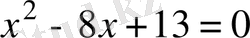 .
.
Жауабы.
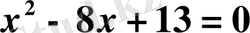 . А) .
. А) .
4.
Теңдеуді шешіңіз:
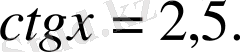
А)
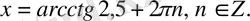
B)
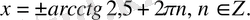
C)
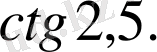
D)
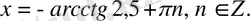
E)
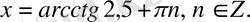
Шешуі.
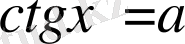 теңдеуінің шешімі
теңдеуінің шешімі
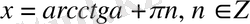 түрінде жазылатынын ескерсек, теңдеудің шешімін бірден табамыз:
түрінде жазылатынын ескерсек, теңдеудің шешімін бірден табамыз:
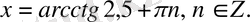
Жауабы.
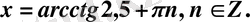 Е) .
Е) .
5. 72 санын 12, 5 % кемітіңіз.
А) 9.
B) 63.
C) 64, 8.
D) 11.
E) 70, 2.
Шешуі. 72 - ∙72 = 72 - 0, 125∙72 = 72 - 9 = 63.
Жауабы. 63. B) .
6.
Теңсіздікті шешіңіз:
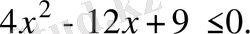
А) 1.
B) 2, 5 .
C) 3, 5.
D) 1, 5.
E) 4, 5.
Шешуі.
1
-тәсіл
. Алдымен берілген теңсіздікке сәйкес квадраттық теңдеуді шешеміз, яғни түбірлерін табамыз:
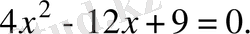 Дискриминанты
Дискриминанты
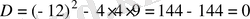 , сондықтан теңдеудің бір ғана түбірі бар:
, сондықтан теңдеудің бір ғана түбірі бар:
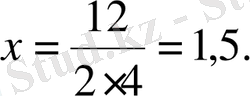 Теңдеудің бас коэффициенті оң, яғни параболаның тармақтары жоғары қараған және теңдеудің бір ғана түбірі бар болғандықтан, квадрат үшмүшенің графигі абсцисса өсінен жоғары орналасқан. Сонымен,
Теңдеудің бас коэффициенті оң, яғни параболаның тармақтары жоғары қараған және теңдеудің бір ғана түбірі бар болғандықтан, квадрат үшмүшенің графигі абсцисса өсінен жоғары орналасқан. Сонымен,
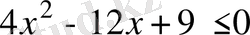 теңсіздігі бір ғана
теңсіздігі бір ғана
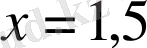 нүктесінде орындалады.
нүктесінде орындалады.
2
- тәсіл
. Берілген теңсіздіктің сол жағы айырманың квадраты екенін ескеріп, оған мәндес теңсіздік аламыз:
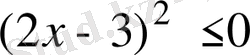 . Квадрат ешқашан теріс болмайтынын ескерсек, соңғы теңсіздіктің
. Квадрат ешқашан теріс болмайтынын ескерсек, соңғы теңсіздіктің
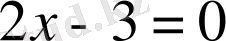 теңдеуімен мәндес екенін көреміз, яғни
теңдеуімен мәндес екенін көреміз, яғни
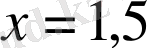 .
.
Жауабы.
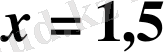 .
D) .
.
D) .
7.
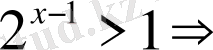
Теңсіздіктің дұрыс шешімін анықтаңыз:
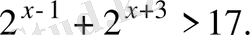
А)
2
х
B)
1
х
C)
2
х
D)
1
х
E)
1
х
Шешуі.
1
-тәсіл
.
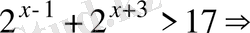
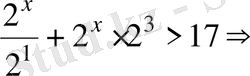
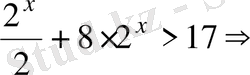

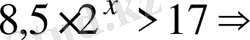

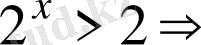
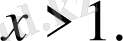
2
-тәсіл
.
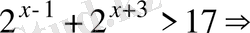
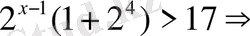
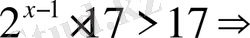

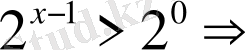
 .
.
Жауабы.
1
х
В) .
8.
Есептеңіз:
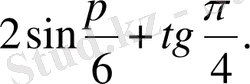
А)
.
B)
.
C)
.
D) 2.
E)
.
Шешуі.
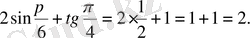
Жауабы. 2. D) .
9. 1-ден 135-ке дейінгі (135-ті қоса санағанда) барлық тақ сандардың қосындысын табыңыз.
А) 4624.
B) 4556.
C) 4623.
D) 4692.
E) 4554.
Шешуі.
Берілген сандар бірінші мүшесі
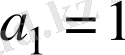 , соңғы (68-ші) мүшесі
, соңғы (68-ші) мүшесі
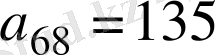 , ал айырмасы
, ал айырмасы
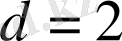 болатын арифметикалық прогрессия құрайды. Арифметикалық прогрессияның алғашқы
болатын арифметикалық прогрессия құрайды. Арифметикалық прогрессияның алғашқы
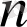 мүшесінің қосындысының формуласын қолданамыз:
мүшесінің қосындысының формуласын қолданамыз:
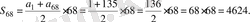
Жауабы. 4624. A) .
10.
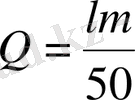 өрнегінің
өрнегінің
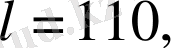
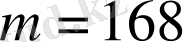 болғандағы сан мәнін табыңыз.
болғандағы сан мәнін табыңыз.
А) 17.
B) 210.
C) 370.
D) 369, 6.
E) - 420.
Шешуі.
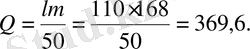
Жауабы. 369, 6. D) .
11.
Өрнекті ықшамдаңыз:
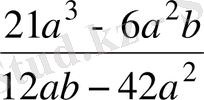 .
.
А)
.
B)
.
C)
.
D)
.
E)
.
Шешуі.
Алымы мен бөлімінде ортақ көбейткіштерді жақша сыртына шығарып, ықшамдаймыз:
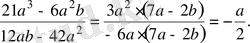
Жауабы.
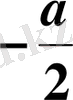 .
A) .
.
A) .
12.
Теңдеулер жүйесін шешіңіз:
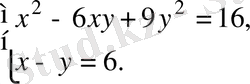
А) шешімі жоқ.
B) (7; 1), (11; 5) .
C) (-7; -1), (-6; -5) .
D) (3; 6), (9; -5) .
E) (8; -4), (0; 9) .
Шешуі.
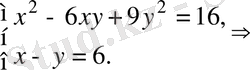
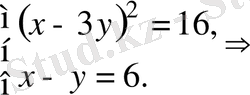
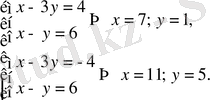
Сонымен, жүйенің екі шешімі бар: (7; 1), (11; 5) .
Жауабы. (7; 1), (11; 5) . В) .
13.
Теңсіздіктер жүйесін шешіңіз:
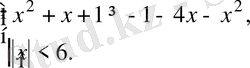
А) (-∞; -6)
(-2; -0, 5) .
B) (-6; 2)
(6; + ∞) .
C) (-6; -2)
(-0, 5; 6) .
D) (-2; -0, 5)
(6; + ∞) .
E) (-6; -2]
[-0, 5; 6) .
Шешуі.
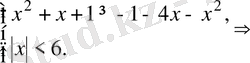
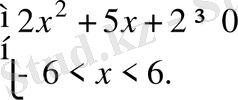
Жүйедегі квадраттық теңсіздікті шешеміз:
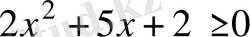 . Ол үшін алдымен оған сәйкес квадраттық теңдеуді шешеміз:
. Ол үшін алдымен оған сәйкес квадраттық теңдеуді шешеміз:
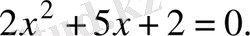 Дискриминант
Дискриминант
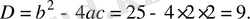 Сонда теңдеудің түбірлері:
Сонда теңдеудің түбірлері:
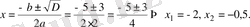
Бас коэффициенті оң болғандықтан квадраттық теңсіздіктің шешімі
 болады. Бұл шешімнің жүйедегі екінші
болады. Бұл шешімнің жүйедегі екінші
 теңсіздігімен қиылысуы есептің жауабын береді:
теңсіздігімен қиылысуы есептің жауабын береді:
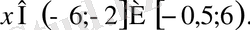
Жауабы.
 .
Е) .
.
Е) .
14.
Анықталу облысын табыңыз:
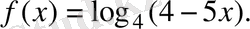
А) (1; ∞) .
B) (- ∞; - 0, 8) .
C) (- ∞; 0, 8) .
D) (- ∞; 0) .
E) (0, 8; ∞) .
Шешуі.
Логарифмнің анықтамасы бойынша логарифм астындағы өрнек оң болуы керек, сондықтан
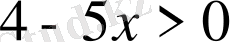 болуы керек. Бұдан
болуы керек. Бұдан
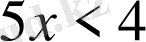 теңсіздігі шығады немесе
теңсіздігі шығады немесе
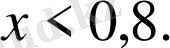
Жауабы.
 .
С) .
.
С) .
15.
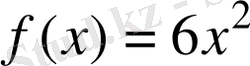 функциясы берілген.
функциясы берілген.
 есептеңіз.
есептеңіз.
А) 14.
B) 28.
C) 16.
D) 24.
E) 8.
Шешуі.
Тұрақтыны туынды таңбасының алдына шығаруға болатыны туралы теореманы және дәрежелік функцияның туындысының формуласын пайдаланамыз:
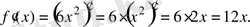 Алынған туындыда айнымалы орнына берілген мәнін қоямыз:
Алынған туындыда айнымалы орнына берілген мәнін қоямыз:
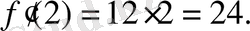
Жауабы. 24. D) .
16.
Функцияның туындысын табыңыз:
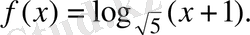
А)
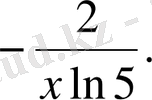
B)
.
C)
.
D)
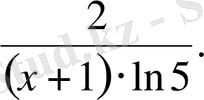
E)
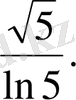
Шешуі. 1 -тәсіл . Логарифмдік функцияны және күрделі функцияны дифференциалдау ережелерін қолданамыз:
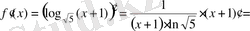
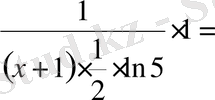
=
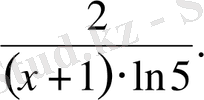
2 -тәсіл . Алдымен логарифмнің қасиеттерін қолдана отырып берілген функцияны түрлендіріп аламыз:
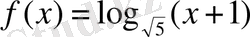

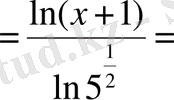
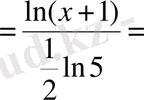
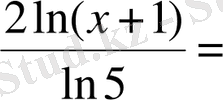
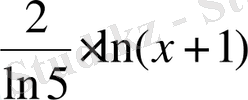 .
.
Енді туынды табамыз:
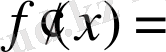
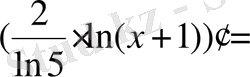
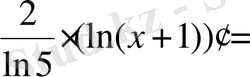
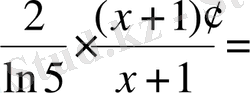
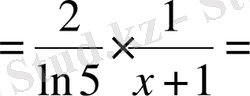
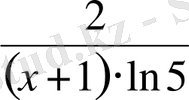 .
.
Жауабы.
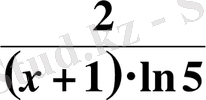 . D) .
. D) .
17. Сырттай сызылған шеңбердің радиусы 6 см, ал қарсы жатқан бұрыш 45º-қа тең болатын үшбұрыштың қабырғасын табыңыз.
А) 6 см.
B)
см.
C)
см.
D) 3 см.
E)
см.
Шешуі.
Синустар теоремасы бойынша
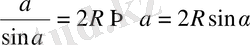 , яғни ізделінді қабырға
, яғни ізделінді қабырға
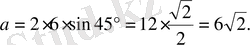
Жауабы.
 .
B) .
.
B) .
18.
Егер тіктөртбұрыштың қабырғалары 6 см және 6
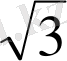 см болса, диагональдары арасындағы кіші бұрышын табыңыз.
см болса, диагональдары арасындағы кіші бұрышын табыңыз.
А) 135º.
B) 45º.
C) 60º.
D) 120º.
E) 100º.
Шешуі.
Тіктөртбұрыштың қабырғалары
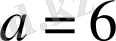 см және
см және
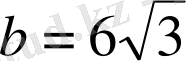 см делік. Бір жағынан тіктөртбұрыш ауданы
см делік. Бір жағынан тіктөртбұрыш ауданы
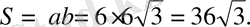 Екінші жағынан, кез келген дөңес төртбұрыштың ауданын
Екінші жағынан, кез келген дөңес төртбұрыштың ауданын
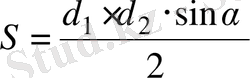 , мұндағы
, мұндағы
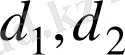 − төртбұрыштың диагональдары, ал
− төртбұрыштың диагональдары, ал
 − олардың арасындағы бұрыш, формуласымен есептеуге болатынын ескерсек, онда
− олардың арасындағы бұрыш, формуласымен есептеуге болатынын ескерсек, онда
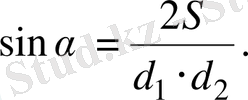 Тіктөртбұрышта
Тіктөртбұрышта
 болады; диагональді
болады; диагональді
 арқылы белгілесек, Пифагор теоремасы бойынша
арқылы белгілесек, Пифагор теоремасы бойынша
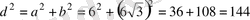 . Сонымен,
. Сонымен,
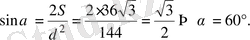
Жауабы. 60º. С) .
19. Тік бұрышты үшбұрыштың ауданы 150-ге, катеттерінің біреуі 15-ке тең. Тік бұрышының төбесінен түсірілген биіктіктің ұзындығын табыңыз.
А) 12.
B) 24.
C)
.
D)
.
E) 20.
c
h c
Шешуі.
Тік бұрышты үшбұрыштың катеттерінің белгілісі
 , белгісізі
, белгісізі
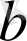 делік. Тік бұрышты үшбұрыштың ауданы
делік. Тік бұрышты үшбұрыштың ауданы
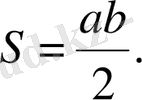 Екінші жағынан
Екінші жағынан
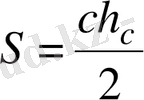 , мұндағы
, мұндағы
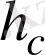 − тік бұрыштың төбесінен түсірілген, яғни гипотенузаға түсірілген биіктік. Есеп шарты бойынша берілген үшбұрыш ауданы
− тік бұрыштың төбесінен түсірілген, яғни гипотенузаға түсірілген биіктік. Есеп шарты бойынша берілген үшбұрыш ауданы
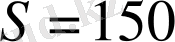 , яғни
, яғни
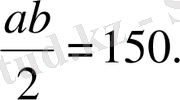 Бұдан
Бұдан
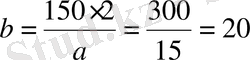 . Пифагор
. Пифагор
a
b
теоремасы бойынша гипотенуза
Әрі қарай
a
Жауабы. 12. А) .
20. 60º - қа тең АСВ бұрышының қабырғалары центрі О 1 және О 2 болып келетін және өзара жанасатын шеңберлерді жанайды ( О 2 - кіші шеңбердің центрі) . СО 1 =12 см. Центрі О 2 болып келетін шеңбердің радиусын табыңыз.
А)
см.
B)
см.
C) 3 см.
D)
см.
E) 2 см.
Шешуі.
,
нүктелері
бұрышына іштей сызылған шеңберлердің центрлері болғандықтан
бұрышының биссектрисасына тиісті болады, яғни
.
мен
арқылы
түзуінің сәйкесінше үлкен және кіші шеңберлермен жанасу нүктелерін белгілейік.
және
болатыны түсінікті.
және
үшбұрыштары тікбұрышты және ұқсас болады (
бұрышы ортақ) . Тікбұрышты үшбұрышта
бұрышқа
B BBC
A C
O 1 BBC
O 2 2 1 BBC
KBBC
NBBC
C BBC
LB BBC
PB BBC
қарсы катет гипотенузаның жартысына тең болғандықтан,
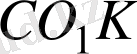
үшбұрышынан
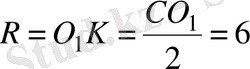 . Екі шеңбердің жанасу нүктесін
. Екі шеңбердің жанасу нүктесін
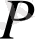 арқылы белгілейік.
арқылы белгілейік.
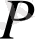 нүктесі
нүктесі
 биссектрисасына тиісті болады, себебі екі шеңбердің жанасу нүктесі олардың центрлерін қосатын кесіндіге тиісті болады, ал екі шеңбердің центрлері
биссектрисасына тиісті болады, себебі екі шеңбердің жанасу нүктесі олардың центрлерін қосатын кесіндіге тиісті болады, ал екі шеңбердің центрлері
 биссектрисасына тиісті. Кіші шеңбердің радиусы
биссектрисасына тиісті. Кіші шеңбердің радиусы
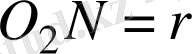 болсын.
болсын.
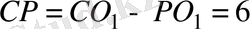 болатыны көрініп тұр.
болатыны көрініп тұр.
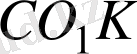 және
және
 үшбұрыштарының ұқсастығынан
үшбұрыштарының ұқсастығынан
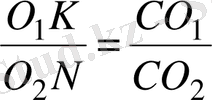 немесе
немесе
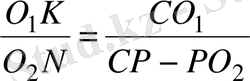 , яғни
, яғни
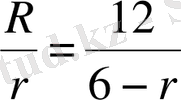 немесе
немесе
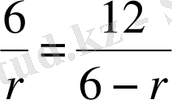 . Соңғы теңдеуді
. Соңғы теңдеуді
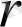 -ға қатысты шешсек,
-ға қатысты шешсек,
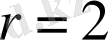 екендігі шығады.
екендігі шығады.
Жауабы. 2. Е) .
21. AB =5; BC =13; CD =9; DA =15; AC =12 болатын ABCD төртбұрышының ауданын табыңыз.
А) 88.
B) 98.
C) 84.
D) 104.
E) 108.
Шешуі.
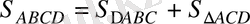 .
.
A
BA
C
DCBA
Екі үшбұрыштың аудандарын Герон формуласын қолданып табуға болады:
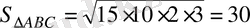 ,
,
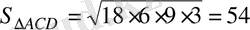 .
.
Сонымен,
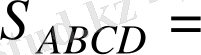
 .
.
2
-тәсіл.
 және
және
 үшбұрыштарының тікбұрышты үшбұрыштар екендігін байқасақ (егер қабырғалары
үшбұрыштарының тікбұрышты үшбұрыштар екендігін байқасақ (егер қабырғалары
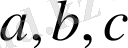 болатын үшбұрыштың қабырғалары үшін
болатын үшбұрыштың қабырғалары үшін
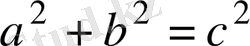 теңдігі орындалса, онда үшбұрыш гипотенузасы
теңдігі орындалса, онда үшбұрыш гипотенузасы
 - ға тең тікбұрышты үшбұрыш болады; біздің жағдайымызда
- ға тең тікбұрышты үшбұрыш болады; біздің жағдайымызда
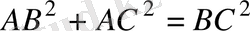 және
және
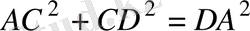 ), онда есеп жеңілірек шығады:
), онда есеп жеңілірек шығады:
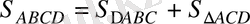
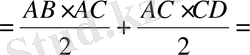
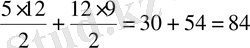 .
.
Жауабы. 84. C) .
22.
 -нің қандай мәнінде
-нің қандай мәнінде
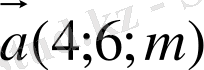 және
және
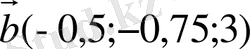 векторлары коллинеар болады?
векторлары коллинеар болады?
А) -8.
B) 4.
C) -24.
D) 1.
E) -4.
Шешуі.
Екі вектордың коллинеар болуының қажетті және жеткілікті шартын қолданамыз:
 . Бұдан
. Бұдан
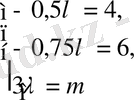 жүйесін аламыз. Жүйені шешеміз:
жүйесін аламыз. Жүйені шешеміз:
 .
.
Жауабы. -24. C) .
23. A (1; 3; -2), B (-5; 7; 8) нүктелері берілген. М нүктесі АВ кесіндісінің ортасы болса, М нүктесінің координаталарын табыңыз.
А) М (5; -2; 5) .
B) М (-2; 5; 3) .
C) М (3; 5; 5) .
D) М (-2; 5; 5) .
E) М (5; 5; 3) .
Шешуі.
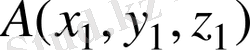 және
және
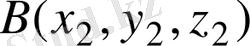 нүктелерін қосатын кесіндінің ортасының координаталарының формулаларын қолданамыз:
нүктелерін қосатын кесіндінің ортасының координаталарының формулаларын қолданамыз:
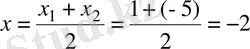 ,
,
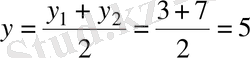 ,
,
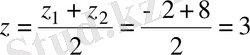 .
.
Жауабы. М (-2; 5; 3) . В) .
24. Тік бұрышты параллелепипедтің үш өлшемі 2 см, 3 см, 6 см. Оның диагоналінің ұзындығын табыңыз.
А) 8 см.
B) 9 см.
C) 11 см.
D) 7 см.
E) 6 см.
Шешуі.
Тік бұрышты параллелепипедтің диагоналі
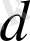 оның үш өлшемі
оның үш өлшемі
 ,
,
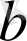 және
және
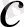 арқылы былайша өрнектеледі:
арқылы былайша өрнектеледі:
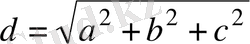 . Осы формулаға есептің берілгендерін қойсақ:
. Осы формулаға есептің берілгендерін қойсақ:
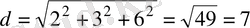 (см) .
(см) .
Жауабы . 7 см. D) .
25. Конус қандай фигураны айналдырғанда шығады?
А) Тік бұрышты үшбұрышты катеті арқылы айналдырғанда.
B) Дөңгелекті диаметрі арқылы айналдырғанда.
C) Тік бұрышты үшбұрышты гипотенуза арқылы айналдырғанда.
D) Тең бүйірлі үшбұрышты бүйір қабырғасы арқылы айналдырғанда.
E) Тік төртбұрышты диагоналі арқылы айналдырғанда.
Шешуі. Тік бұрышты үшбұрышты катеті арқылы айналдырғанда конус шығады.
Жауабы. Тік бұрышты үшбұрышты катеті арқылы айналдырғанда. А) .
2-нұсқа
1. Пішіні квадрат тәрізді жер бөлігінің сызбасы 1:500 масштабымен жасалған. Оның қабырғасы сызбада 16 см. Осы жер бөлігінің ауданын есептеп табыңыз.
А) 6400 м 2 .
B) 64000 м 2 .
C) 6, 4 м 2 .
D) 64 м 2 .
E) 640 м 2 .
Шешуі. Квадрат қабырғасын x арқылы белгілесек, есеп шартынан 1:500 = 16: x теңдеуін (пропорция) аламыз. Бұл теңдеуден x =(500∙16) :1=8000 см=80 м. Сонымен, S = x 2 = 6400 м 2 .
Жауабы. 6400 м 2 . А) .
2.
Есептеңіз:
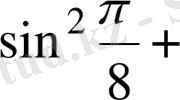
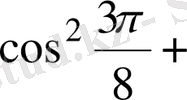
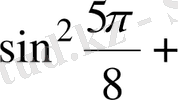
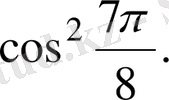
А) 3.
B) -1.
C) 2.
D) 4.
E) 1.
Шешуі. 1 -тәсіл. Дәрежені төмендету формулаларын қолданамыз:
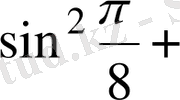
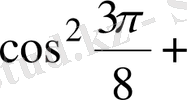
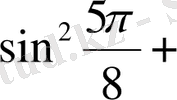
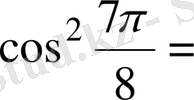
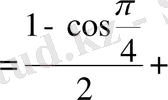
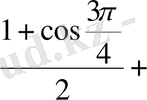
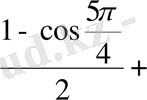
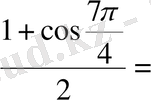
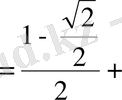
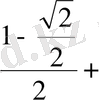
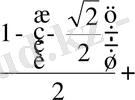
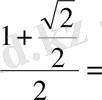
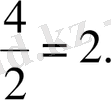
2 -тәсіл. Келтіру формулаларын қолданамыз:
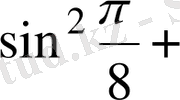
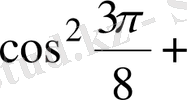
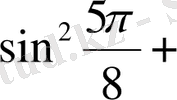
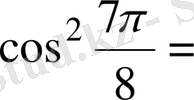
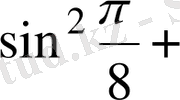
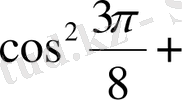
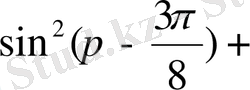
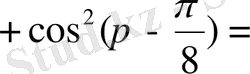
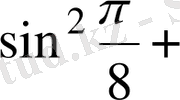
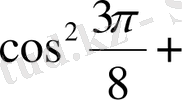
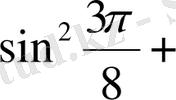
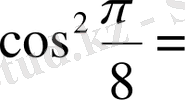
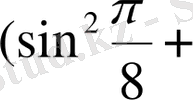
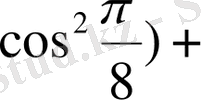
+
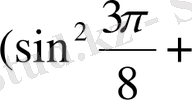
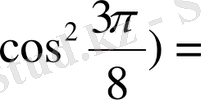 1+1=2.
1+1=2.
Жауабы. 2. C) .
3.
Функцияның өсу аралығын табыңыз:
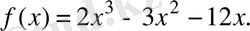
А)
.
B)
.
C)
.
D)
.
E)
.
Шешуі. Функцияның туындысын тауып, туындының таңбасы тұрақты болатын аралықтарды анықтаймыз; туынды оң болатын аралықтарда функция өседі.
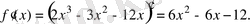

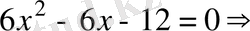
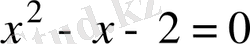 . Түбірлері:
. Түбірлері:
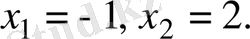
Жауабы.
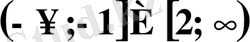 .
В) .
.
В) .
4.
Теңдеулер жүйесін шешіңіз:
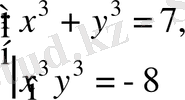 .
.
A)
,
.
B)
,
.
C)
,
.
D)
,
.
E)
,
.
Шешуі:
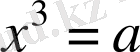 ,
,
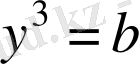 алмастыруын енгізіп, жүйені
алмастыруын енгізіп, жүйені
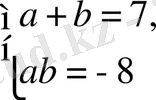
түріне келтіреміз.
Оның шешімдері:
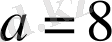 ,
,
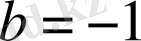 немесе
немесе
 ,
,
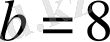 . Бұдан
. Бұдан
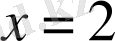 ,
,
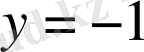 немесе
немесе
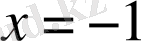 ,
,
 .
.
Жауабы. (2; -1), (-1; 2) . C) .
5.
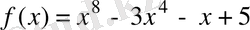 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
А)
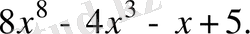
B)
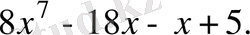
C)
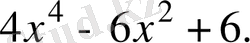
D)
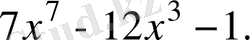
E)
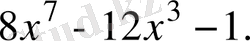
Шешуі.
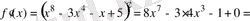
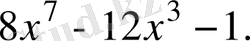
Жауабы.
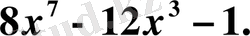 E) .
E) .
6. Кубтың диагоналі 12 см-ге тең. Кубтың көлемін табыңыз.
А) 216 см 3 .
B) 144 см 3 .
C) 216
см 3 .
D) 144
см 3 .
E) 192
см 3 .
Шешуі.
Тік бұрышты параллелепипедтің диагоналі
 оның үш өлшемі
оның үш өлшемі
 ,
,
 және
және
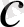 арқылы былайша өрнектеледі:
арқылы былайша өрнектеледі:
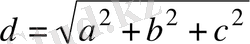 . Куб барлық қырлары тең тікбұрышты параллелепипед болғандықтан
. Куб барлық қырлары тең тікбұрышты параллелепипед болғандықтан
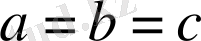 , сондықтан
, сондықтан
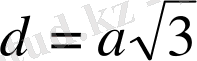 . Бұдан
. Бұдан
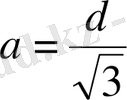 екендігі шығады. Кубтың көлемі
екендігі шығады. Кубтың көлемі
 немесе
немесе
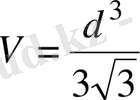 . Есептің шарты бойынша
. Есептің шарты бойынша
 см. Олай болса,
см. Олай болса,
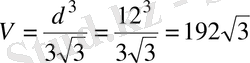 (см
3
) .
(см
3
) .
Жауабы.
192
 см
3
.
E) .
см
3
.
E) .
7. Теплоход белгілі бір жылдамдықпен 72 км жол жүруі керек еді. Ол іс жүзінде жолдың бірінші жартысын белгіленген жылдамдықтан 3 км/сағ-қа кем, ал екінші жартысын 3 км/сағ-қа артық жылдамдықпен жүріп өтті. Теплоход барлық жолға 5 сағат уақыт жұмсады. Теплоход қанша уақытқа кешікті?
A) 10 мин.
B) 12 мин.
C) 14 мин.
D) 18 мин.
E) 11 мин.
Шешуі.
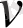 - теплоходтың бастапқы жылдамдығы. Есеп шартынан оның барлық жолға жұмсаған уақытына қатысты
- теплоходтың бастапқы жылдамдығы. Есеп шартынан оның барлық жолға жұмсаған уақытына қатысты
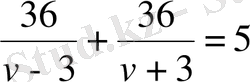 теңдеуін аламыз. Бұдан
теңдеуін аламыз. Бұдан
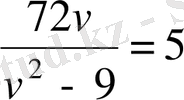 немесе
немесе
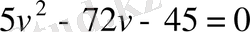 квадрат теңдеуі шығады. Оны шешсек
квадрат теңдеуі шығады. Оны шешсек
 және
және
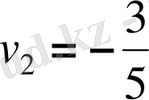 , яғни
, яғни
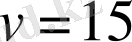 км/сағ, себебі жылдамдық теріс бола алмайды. Бастапқы жылдамдықпен жүргенде жұмсалатын уақыт
км/сағ, себебі жылдамдық теріс бола алмайды. Бастапқы жылдамдықпен жүргенде жұмсалатын уақыт
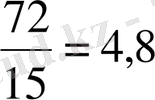 сағ. Кешіккен уақыт
сағ. Кешіккен уақыт
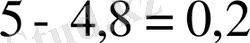 cағат, яғни 12 минут.
cағат, яғни 12 минут.
Жауабы. 12 минут. B) .
8. Құс фермасында қаздар үйрекке қарағанда 2 есе көп еді. Біраз уақыттан кейін қаздар саны 20 %-ке, ал үйрек саны 30 %-ке өсті. Сонда қаздар мен үйректер сандары барлығы 8400 басқа өскені анықталды. Құс фермасында қаздардың саны қанша және үйректер саны қанша болды?
A) 24000 қаз, 12000 үйрек.
B) 26800 қаз, 17600 үйрек.
C) 28800 қаз, 15600 үйрек.
D) 30600 қаз, 18600 үйрек.
E) 32800 қаз, 20800 үйрек.
Шешуі.
 - қаздар,
- қаздар,
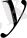 - үйректер (бастапқы) саны. Есеп шарттарынан
- үйректер (бастапқы) саны. Есеп шарттарынан
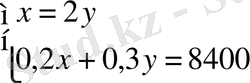 теңдеулер жүйесін аламыз да, оны шешеміз:
теңдеулер жүйесін аламыз да, оны шешеміз:
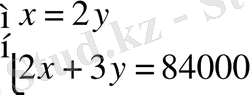 ,
,
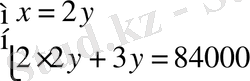 ,
,
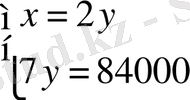 ,
,
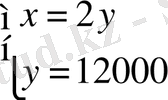 ,
,
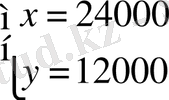 , Сонымен, бастапқыда 24000 үйрек және 12000 қаз болған, ал соңында
, Сонымен, бастапқыда 24000 үйрек және 12000 қаз болған, ал соңында
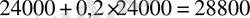 үйрек,
үйрек,
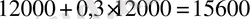 қаз.
қаз.
Жауабы. 28800 қаз, 15600 үйрек. C) .
9.
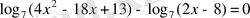 теңдеуін шешіңіз.
теңдеуін шешіңіз.
A) 1, 5.
B) 1, 5; 3, 5.
C) 1; 3.
D) 3; 5.
E) Түбірі жоқ.
Шешуі.
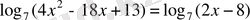 ,
,
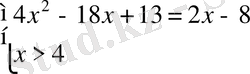 ,
,
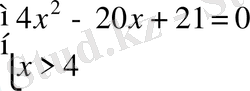 ,
,
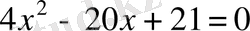 ,
,
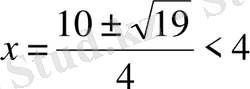 , ø.
, ø.
Жауабы . Түбірі жоқ. C) .
10.
Теңдеуді шешіңіз:
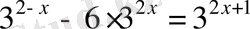 .
.
A) 6.
B) 4.
C) 2.
D) 1.
E) 0.
Шешуі.
Дәреженің қасиеттерін пайдаланып, теңдеуді түрлендіреміз:
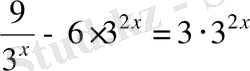 ,
,
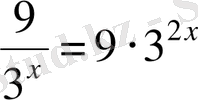 ,
,
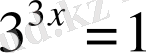 ,
,
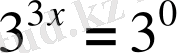 ,
,
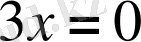 ,
,
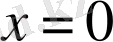 .
.
Жауабы . 0. E) .
11.
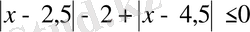 теңсіздігінің неше бүтін шешімі бар?
теңсіздігінің неше бүтін шешімі бар?
A) 3.
B) 4.
C) 2.
D) 0.
E) ∞.
Шешуі.
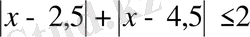 ,
,
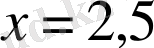

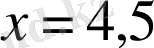 .
.
 -тен 2, 5 пен 4, 5 нүктелеріне дейінгі қашықтықтардың қосындысы 2-ден артық емес дегенді білдіреді. 2, 5 пен 4, 5 нүктелерінің ара қашықтығы 2-ге тең. Сондықтан, есеп шартын
-тен 2, 5 пен 4, 5 нүктелеріне дейінгі қашықтықтардың қосындысы 2-ден артық емес дегенді білдіреді. 2, 5 пен 4, 5 нүктелерінің ара қашықтығы 2-ге тең. Сондықтан, есеп шартын
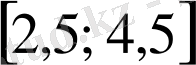 кесіндісіне тиісті нүктелер ғана қанағаттандыратынын көреміз және бұл кесіндіге тиісті екі-ақ бүтін сан бар: 2 және 3 сандары.
кесіндісіне тиісті нүктелер ғана қанағаттандыратынын көреміз және бұл кесіндіге тиісті екі-ақ бүтін сан бар: 2 және 3 сандары.
2, 5
4, 5
-
-
+
Жауабы. 2. C) .
12.
Есептеңіз:
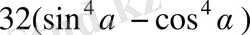 , егер
, егер
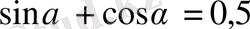 .
.
A)
.
B)
.
C)
.
D)
.
E)
.
Шешуі.
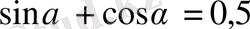

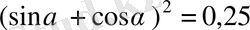


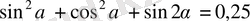


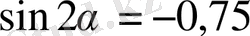

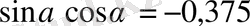


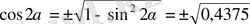 .
.
Сонда
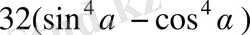
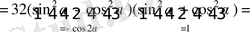
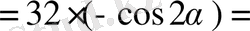
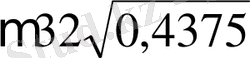 .
.
Жауабы.
 .
A) .
.
A) .
13.
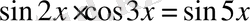 .
.
A)
,
.
B)
,
;
,
.
C)
,
.
D)
,
;
,
.
E)
,
.
Шешуі.
1
-тәсіл.
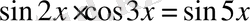

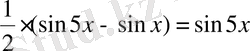




 ; 1)
; 1)
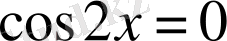 ;
;
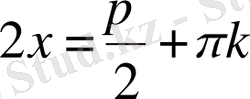 ;
;
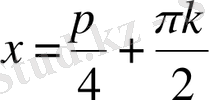 ,
,
 ; 2)
; 2)
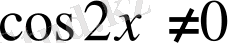

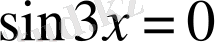 ;
;
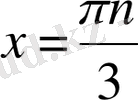 ,
,
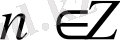 .
.
2
-тәсіл.
 екенін ескерсек жоғарыдағы
екенін ескерсек жоғарыдағы
 теңдеуіне келеміз.
теңдеуіне келеміз.
Жауабы.
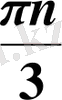 ,
,
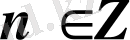 ;
;
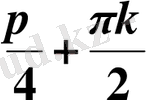 ,
,
 .
D) .
.
D) .
14.
Теңсіздікті шешіңіз:
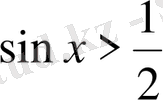 .
.
A)
,
.
B)
,
.
C)
,
.
D)
,
.
E)
,
.
Шешуі:
Суреттен
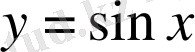 функциясы өзінің негізгі анықталу облысы болатын
функциясы өзінің негізгі анықталу облысы болатын
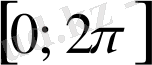 аралығының
аралығының
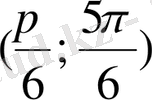 интервалында берілген
интервалында берілген
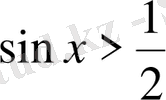 теңсіздігін қанағаттандыратынын көреміз. Оған функцияның периодын қосып есептің жауабын аламыз:
теңсіздігін қанағаттандыратынын көреміз. Оған функцияның периодын қосып есептің жауабын аламыз:
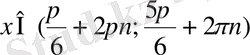 ,
,
 .
.
π/6
х
у
О
1
1/2
5π/6
Жауабы.
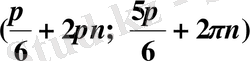 ,
,
 . B) .
. B) .
15.
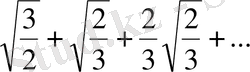 қосындысын табыңыз.
қосындысын табыңыз.
A)
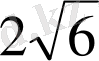 .
.
B)
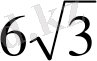 .
.
C)
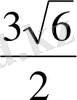 .
.
D)
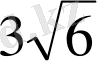 .
.
E)
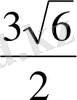 .
.
Шешуі.
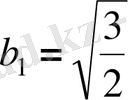 ,
,
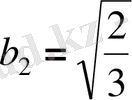 ,
,
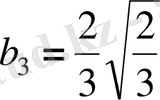 деп белгілейік те,
деп белгілейік те,
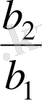 ,
,
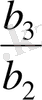 қатынастарын есептейік:
қатынастарын есептейік:
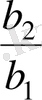
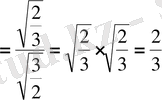 және
және
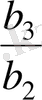
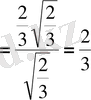 .
.
Бұл бірінші мүшесі
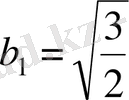 , еселігі
, еселігі
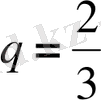 болатын шексіз кемімелі геометриялық прогрессия. Сондықтан шексіз кемімелі геометриялық прогрессияның қосындысының формуласы бойынша
болатын шексіз кемімелі геометриялық прогрессия. Сондықтан шексіз кемімелі геометриялық прогрессияның қосындысының формуласы бойынша
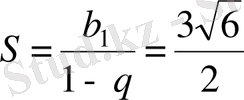 .
.
Жауабы.
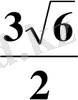 . C) .
. C) .
16.
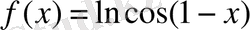 функциясының туындысын табыңыз.
функциясының туындысын табыңыз.
A) 1/(sin(1-x) ) .
B) tg(1-x) .
C) -1/(cos(1-x) ) .
D) tg(x-1) .
E) sin(1-x) .
Шешуі
.
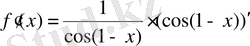 =
=
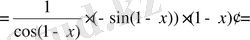
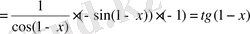 .
.
Жауабы.
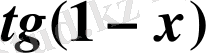 . B) .
. B) .
17.
Мына сызықтармен шектелген фигура ауданын есептеңіз:
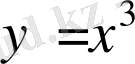 ,
,
 ,
,
 .
.
A) 4.
B) 12.
C) 1.
D) 5.
E) 6.
Шешуі .
Ньютон-Лейбниц формуласын қолданамыз:
y
xy
O
2 bxy
y=x 3
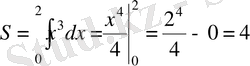 .
.
Жауабы. 4. A) .
18.
Қабырғалары
 және
және
 болатын
болатын
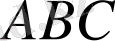 үшбұрышы берілген және осы қабырғалар арасындағы бұрышы
үшбұрышы берілген және осы қабырғалар арасындағы бұрышы
 болсын.
болсын.
 төбесінен шығатын биссектрисаның ұзындығы неге тең?
төбесінен шығатын биссектрисаның ұзындығы неге тең?
A)
.
B)
.
C)
.
D)
.
E)
.
C
B
A
b
C/2
C/2
a
l
D
Шешуі
. Суреттегідей белгілеулер енгізіп, аудандар тәсілін қолданамыз.
 ,
,
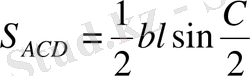 ,
,
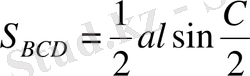 .
.
Сонда есеп шартынан:
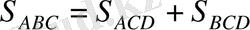


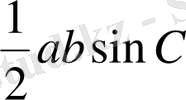
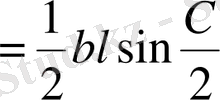
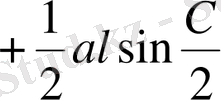


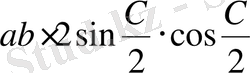
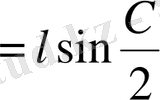
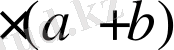


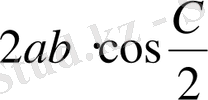
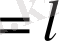

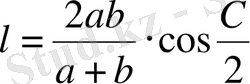 .
.
Жауабы
.
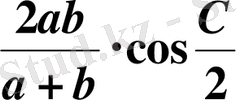 .
E) .
.
E) .
19.
 параллелограмының үш төбесінің координаталары берілген:
параллелограмының үш төбесінің координаталары берілген:
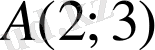 ,
,
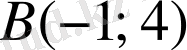 және
және
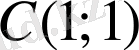 . Төртінші
. Төртінші
 төбесінің координаталарын табыңыз.
төбесінің координаталарын табыңыз.
A) (2; 1) .
B) (0; 4) .
C) (5; 1) .
D) (4; 1) .
E) (4; 0) .
Шешуі.
1-
тәсіл
. Параллелограмның диагональдары қиылысу нүктесінде қақ бөлінеді.
 диагональдардың қиылысу нүктесі болсын. Кесіндінің ортасының формуласын екі рет қолданамыз.
диагональдардың қиылысу нүктесі болсын. Кесіндінің ортасының формуласын екі рет қолданамыз.
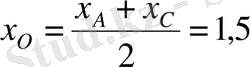 ,
,
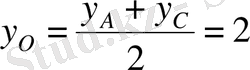 .
.
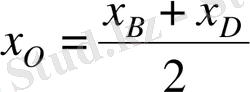

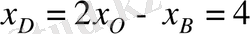 ; тап осылайша
; тап осылайша
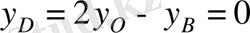 .
.
A
D
B
C
О
Сонымен,
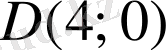 .
.
2-
тәсіл
.
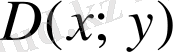 делік. Параллелограмның қарама-қарсы қабырғалары тең болатындықтан
делік. Параллелограмның қарама-қарсы қабырғалары тең болатындықтан
 және
және
 векторлары тең болуы керек. Вектордың координаталарын табу үшін оның ұшының координаталарынан басының сәйкес координаталарын азайтады:
векторлары тең болуы керек. Вектордың координаталарын табу үшін оның ұшының координаталарынан басының сәйкес координаталарын азайтады:
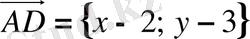 және
және
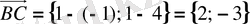 . Тең векторлардың сәйкес координаталары тең болатындықтан:
. Тең векторлардың сәйкес координаталары тең болатындықтан:
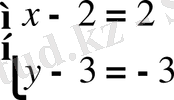 . Бұдан
. Бұдан
 және
және
 .
.
A
D
B
C
3-
тәсіл
.
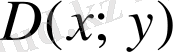 делік. «Қозғалыс» тақырыбын еске түсірейік. Параллелограм-ның қарама-қарсы қабырғалары тең болатындықтан
DC
қабырғасын
AB
қабырғасын параллель көшіру (қозғалыс) арқылы алуға болады. Сонда
C
нүктесі
B
нүктесінің, ал
D
нүктесі
A
нүктесінің бейнесі болады.
C
нүктесінің координаталарын
B
нүктесінің координаталарына сәйкесінше 2 және −3 сандарын қосу арқылы алуға болатыны көрініп тұр. Сондықтан,
D
нүктесінің координаталарын
A
нүктесінің координаталарына сәйкесінше 2 және −3 сандарын қосу арқылы алуға болады, яғни x=2+2=4, y=3+(−3) =0. Сонымен,
делік. «Қозғалыс» тақырыбын еске түсірейік. Параллелограм-ның қарама-қарсы қабырғалары тең болатындықтан
DC
қабырғасын
AB
қабырғасын параллель көшіру (қозғалыс) арқылы алуға болады. Сонда
C
нүктесі
B
нүктесінің, ал
D
нүктесі
A
нүктесінің бейнесі болады.
C
нүктесінің координаталарын
B
нүктесінің координаталарына сәйкесінше 2 және −3 сандарын қосу арқылы алуға болатыны көрініп тұр. Сондықтан,
D
нүктесінің координаталарын
A
нүктесінің координаталарына сәйкесінше 2 және −3 сандарын қосу арқылы алуға болады, яғни x=2+2=4, y=3+(−3) =0. Сонымен,
 және
және
 .
.
A
D
B
C
Жауабы
.
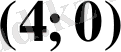 . B) .
. B) .
20. Екі шардың беттерінің аудандарының қатынасы 4:1. Көлемдерінің қатынасын табыңыз.
A) 2:1.
B) 4:1.
C) 6:1.
D) 8:1.
E) 2:3.
Шешуі.
1
-тәсіл
.
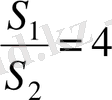

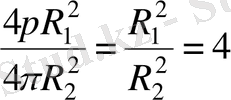

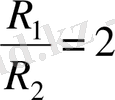 . Көлемдерінің қатынасы
. Көлемдерінің қатынасы
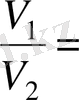
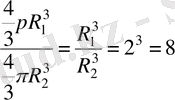

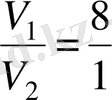 .
.
2 -тәсіл . Кез келген екі шар ұқсас болады. Ұқсас денелердің көлемдері мен беттерінің аудандарының қатынасы
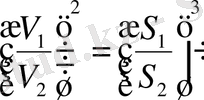 ,
,
бұдан
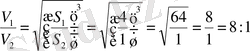 .
.
Сонымен, көлемдерінің қатынасы
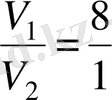 .
.
Жауабы. 8:1. D) .
21. Ұқсас екі төртбұрыштың периметрлерінің қатынасы 2:3. Аудандарының қатынасын табыңыз.
A) 2:3.
B)
:
.
C) 1/2:1/3.
D) 4:9.
E) 6:8.
Шешуі. Ұқсас көпбұрыштар үшін
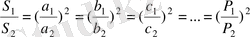
немесе
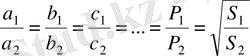 ,
,
яғни ұқсас көпбұрыштардың сәйкес қабырғаларының қатынастары өзара тең. Сонымен,
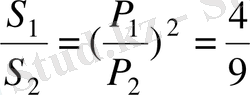 .
.
Жауабы
.
 . D) .
. D) .
22. Қабырғалары 5 см, 12 см және 13 см болатын үшбұрыш берілген. Ұзындығы 13 см-ге тең қабырғасына қарсы жатқан бұрышты табыңыз.
A) 60°.
B) 75°.
C) 90°.
D) 120°.
E) 105°.
Шешуі. Есеп шарттарын пайдаланып үшбұрыш қабырғалары a =5 см, b =12 см, c =13 см делік және 13 см-ге тең қабырғасына қарсы жатқан бұрышты γ арқылы белгілейік.
1 -тәсіл . Косинустар теоремасы бойынша
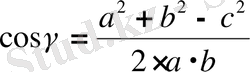
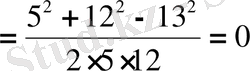

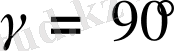 ;
;
2
-тәсіл
.
 екенін байқасақ, Пифагор теоремасы бойынша үшбұрыш - тікбұрышты, яғни
екенін байқасақ, Пифагор теоремасы бойынша үшбұрыш - тікбұрышты, яғни
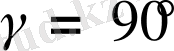 .
.
Жауабы
.
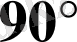 . С) .
. С) .
23.
Теңдеулер жүйесін шешіңіз:
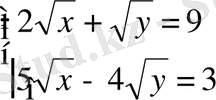 .
.
A) (9; 4) .
B) (16; 1) .
C) (16; 4) .
D) (16; 9) .
E) (9; 9) .
Шешуі
.
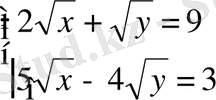 ;
;
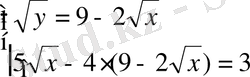 ;
;
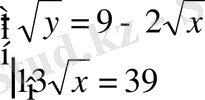 ;
;
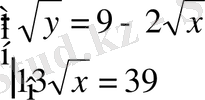 ;
;
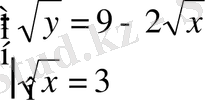 ;
;
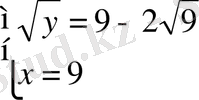 ;
;
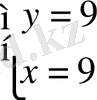 .
.
Жауабы . x=9, y=9. E) .
24.
Теңсіздікті шешіңіз:
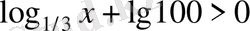 .
.
A) (−∞; 1/9) .
B) (−∞; 9) .
C) (0; 9) .
D) (0; 1/9) .
E) (0; −1/3) .
Шешуі
.
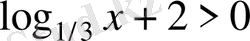 ,
,
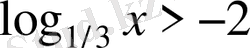 ,
,
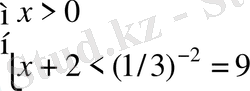 ,
,
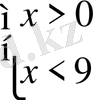 ,
,
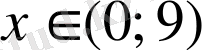 .
.
Жауабы. (0; 9) . C) .
25.
Теңсіздікті шешіңіз:
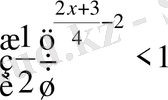 .
.
A) х<2, 5.
B) х>3, 5.
C) х>2, 5.
D) х>4.
E) х<2.
Шешуі
.
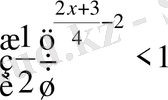 ;
;
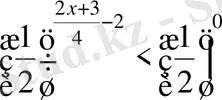 . Көрсеткіштік теңсіздіктің негізі 1/2<1, сондықтан дәреже көрсеткіштері үшін теңсіздік таңбасы қарама-қарсыға өзгереді:
. Көрсеткіштік теңсіздіктің негізі 1/2<1, сондықтан дәреже көрсеткіштері үшін теңсіздік таңбасы қарама-қарсыға өзгереді:
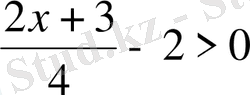 ,
,
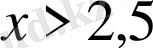 .
.
Жауабы. х>2, 5. C) .
3-нұсқа
1.
 және
және
 сандарының ең үлкен ортақ бөлгішін табыңыз.
сандарының ең үлкен ортақ бөлгішін табыңыз.
A) 2.
B) 6.
C) 9.
D) 4.
E) 3.
Шешуі. Берілген сандарды жай көбейткіштерге жіктейміз де, бір жіктелуден екі жіктелуге де тиісті барлық көбейткіштерді алып, оларды өзара көбейтеміз:
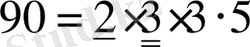 ;
;
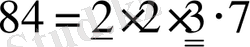 . ЕҮОБ(90; 84)
. ЕҮОБ(90; 84)
 .
.
Жауабы. 6. B) .
2.
Теңдеулер жүйесін шешіңіз:
 .
.
A)
,
.
B)
,
.
C)
,
.
D)
,
.
E)
,
.
Шешуі.
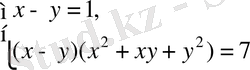 ,
,
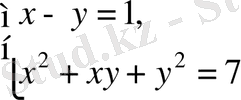 ,
,
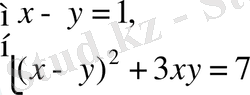 ,
,
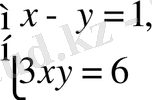 ,
,
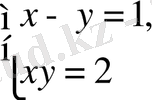 , (2; 1), (-1; -2) .
, (2; 1), (-1; -2) .
Жауабы. (2; 1), (-1; -2) . D) .
3. Құрамындағы никельдің мөлшері 5 % және 40 % болатын болаттың екі түрлі сорты бар. Құрамындағы никельдің мөлшері 30 % болатын 140 т болат алу үшін екі сорттың әрқайсысынан неше тоннадан алу керек?
A) 50 т; 90 т.
B) 40 т; 100 т .
C) 60 т; 80 т.
D) 70 т; 70 т.
E) 80 т; 60 т.
Шешуі.
Болаттың екі түрлі сортын сәйкесінше
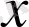 және
және
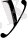 деп белгілесек, есеп шартынан келесі сызықтық теңдеулер жүйесін алып, оны шешеміз:
деп белгілесек, есеп шартынан келесі сызықтық теңдеулер жүйесін алып, оны шешеміз:

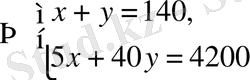
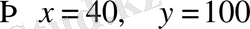 .
.
Жауабы. 40 тонна; 100 тонна. B) .
4. Катер өзен ағысымен 75 км және ағысқа қарсы 75 км жүрді. Катер барлық жолға тынық суда 80 км жүретін уақыттан 2 есе артық жұмсады. Егер ағынның жылдамдығы 5 км/сағ болса, катердің жылдамдығы неге тең?
A)
км/сағ.
B)
км/сағ.
C)
км/сағ.
D) 20 км/сағ.
E) 40 км/сағ.
Шешуі.
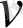 ,
,
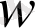 - сәйкесінше катердің және ағыстың жылдамдықтары. Есеп шарттарынан
- сәйкесінше катердің және ағыстың жылдамдықтары. Есеп шарттарынан
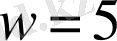 км/сағ,
км/сағ,
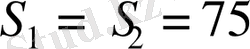 км, және келесі жүйені аламыз:
км, және келесі жүйені аламыз:
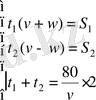

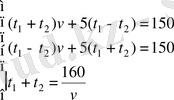

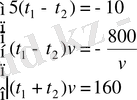


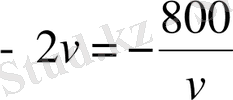

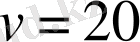 км/сағ.
км/сағ.
Жауабы.
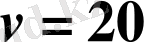 км/сағ. D) .
км/сағ. D) .
5.
Теңдеуді шешіңіз:
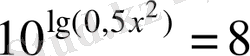 .
.
A) 4.
B) 5.
C)
.
D) 10.
E)
.
Шешуі
. Негізгі логарифмдік теңбе-теңдіктен
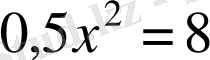 , яғни
, яғни
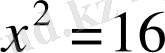 ,
,
 .
.
Жауабы
.
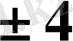 . С) .
. С) .
6.
Теңдеуді шешіңіз:
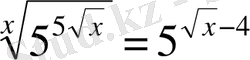 .
.
A) −1.
B) 50.
C) 4.
D) 9.
E) 25.
Шешуі.
Сол жағын түрлендіреміз:
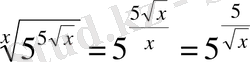 .
.
Сонда
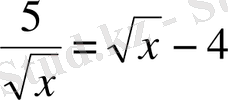 ,
,
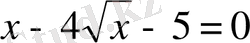 ,
,
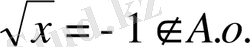 ,
,
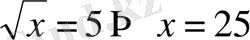 .
.
Жауабы . 25. Е.
7.
Теңсіздікті шешіңіз:
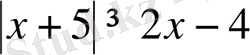 .
.
A)
.
B)
.
C)
.
D)
.
E)
.
Шешуі.
1)
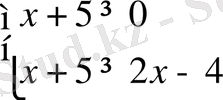 ,
,
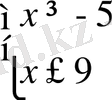 ,
,
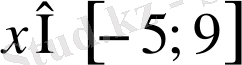 ;
;
2)
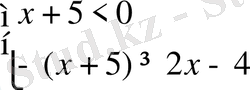 ,
,
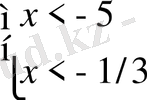 ,
,
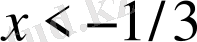 . Сонымен,
. Сонымен,
 .
.
Жауабы
.
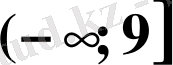 . D) .
. D) .
8.
Өрнекті ықшамдаңыз:
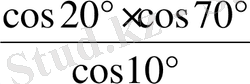 .
.
A)
.
B)
.
C)
.
D)
.
E)
.
Шешуі.
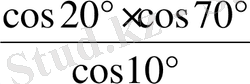
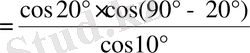
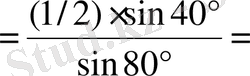
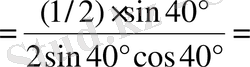
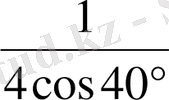 .
.
Жауабы
.
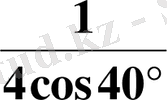 . E) .
. E) .
9.
Теңдеуді шешіңіз:
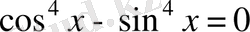 .
.
A)
,
.
B)
,
.
C)
,
.
D) Шешуі жоқ.
E)
,
.
Шешуі.
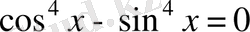

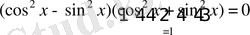


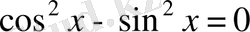

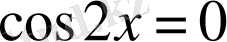 ;
;
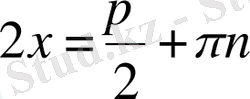 ;
;
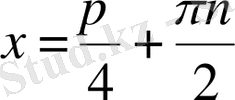 ,
,
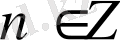 .
.
Жауабы
.
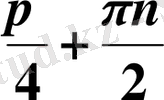 ,
,
 . C) .
. C) .
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz