Параметрге тәуелді есептер: теория, шешу әдістері және ҰБТ-ға арналған мысалдар


Параметрге тәуелді есептер
Жоспар
Кіріспе орнына . . .
Есеп шығару үлгілері . . .
Кіріспе орнына
Жыл сайын жалпы орта мектепті бітіруші түлектер Ұлттық бірыңғай тестілеуде математика пәнінен де емтихан тапсыратыны белгілі. Талапкерлер үшін ҰБТ-да математикадан қиындықтар туғызатын есептер қатарына параметрге қатысты есептерді де жатқызуға болады. Параметрге қатысты есептер, шын мәнінде, оқушылар үшін қиын есептер болып табылады. Бірінші себебі: «Параметр» тақырыбы мектеп математика курсында жеке тақырып болып табылмайды. Екіншіден, мектеп бағдарламасы бойынша мұндай есептер күнделікті сабақтарда қарастырылмайды. Үшіншіден, параметр, бір жағынан, айнымалы болып табылады да, ал екінші жағынан белгілі бір жағдайларда тұрақты деп есептеледі. Осының ара-жігін ажырата білмеуі себепті, оқушы бұл тақырыпқа берілген есептерді шешуде қиындықтарға тіреледі. Мақалада осы тақырыпқа қатысты бірнеше есепті толық шешу жолдарымен келтіреміз.
Есеп шығару үлгілері
1-есеп.
 -ның қандай мәндерінде
-ның қандай мәндерінде
 теңсіздігі орындалады?
теңсіздігі орындалады?
Шешуі.
Квадраттық үшмүше теріс болуы үшін оның бас коэффициенті теріс және дискриминанты теріс болуы керек, яғни
а
параметрі
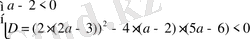 теңсіздіктер жүйесін қанағаттандыруы керек. Осы теңсіздіктер жүйесін шешеміз.
теңсіздіктер жүйесін қанағаттандыруы керек. Осы теңсіздіктер жүйесін шешеміз.
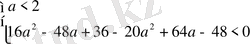
немесе
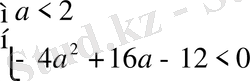
немесе
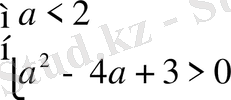
немесе
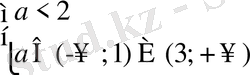 .
.
Бұдан
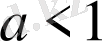 .
.
Жауабы.
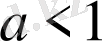 .
.
2-есеп.
Теңдеулер жүйесінің бір ғана шешімі болатындай
а
-параметрінің қабылдайтын бүкіл мәндерін табыңыз:

Шешуі
.
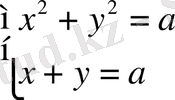 ;
;
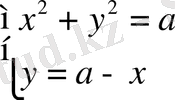 ;
;
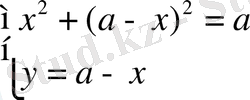 ;
;
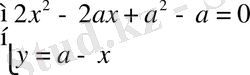 .
.
Теңдеулер жүйесінің бір ғана шешімі болуы үшін оның құрамындағы теңдеулердің әрқайсысының бір-бірден ғана түбірлері болуы керек. Жүйедегі бірінші теңдеу квадраттық теңдеу болып табылады, оның бір ғана шешімі болуы үшін оның дискриминанты нөлге тең болуы керек:
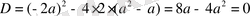

 ,
,
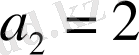 .
.
Жауабы
.
a
=
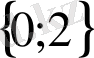 .
.
3-есеп. х-ті табыңыз: 4 + a x = 3x + 1.
Шешуі
. 4 +
a
x = 3x + 1
 (
a
-3) x = -3
(
a
-3) x = -3

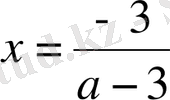

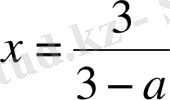 , егер
a
≠ 3; ал
a
= 3 болғанда түбірі жоқ, себебі нөлге бөлуге болмайды.
, егер
a
≠ 3; ал
a
= 3 болғанда түбірі жоқ, себебі нөлге бөлуге болмайды.
Жауабы
.
a
≠ 3 болғанда,
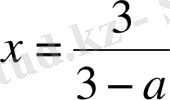 ;
a
= 3 болғанда түбірі жоқ.
;
a
= 3 болғанда түбірі жоқ.
4-есеп.
 -ның қандай мәндерінде
-ның қандай мәндерінде
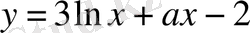 функциясының кризистік нүктелері болмайтынын табыңыз.
функциясының кризистік нүктелері болмайтынын табыңыз.
Шешуі.
Берілген функцияның анықталу облысы:
 . Туындысын табамыз:
. Туындысын табамыз:
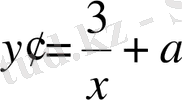 . Оны нөлге теңестіреміз (кризистік нүкте болуының қажетті шарты) :
. Оны нөлге теңестіреміз (кризистік нүкте болуының қажетті шарты) :
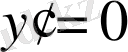 . Яғни
. Яғни
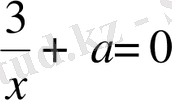 ,
,
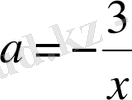

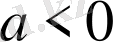 . Бұдан
. Бұдан
 теріс болғанда берілген функцияның кризистік нүктелері бар болады деген шығады. Сонымен,
теріс болғанда берілген функцияның кризистік нүктелері бар болады деген шығады. Сонымен,
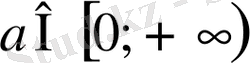 болғанда берілген функцияның кризистік нүктелері жоқ.
болғанда берілген функцияның кризистік нүктелері жоқ.
Жауабы.
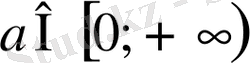 .
.
5-есеп.
 -ның қандай мәндерінде
-ның қандай мәндерінде
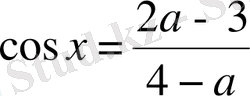 функциясының шешімі бар болады?
функциясының шешімі бар болады?
Шешуі.
Косинус функциясының мәндерінің облысы
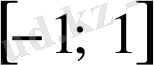 аралығы, сондықтан
аралығы, сондықтан
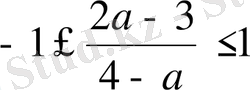 болуы керек.
болуы керек.
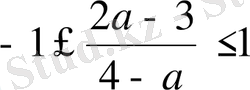

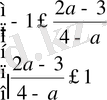


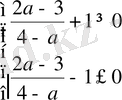

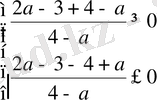

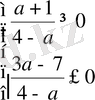


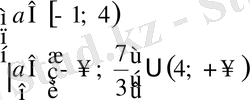

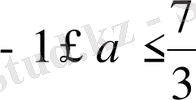
Жауабы.
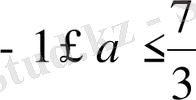 .
.
6-есеп.
 -ның қандай мәнінде
-ның қандай мәнінде
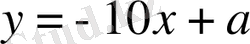 түзуі
түзуі
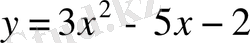 функциясының графигіне жанама болады?
функциясының графигіне жанама болады?
Шешуі.
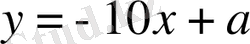 түзуі берілген функция графигіне жанама болатындықтан, берілген функцияның туындысы оның бұрыштық коэффициентіне, яғни
түзуі берілген функция графигіне жанама болатындықтан, берілген функцияның туындысы оның бұрыштық коэффициентіне, яғни
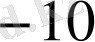 -ға тең болуы керек:
-ға тең болуы керек:
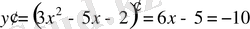

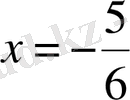 .
.
Жанасу нүктесінде


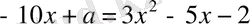

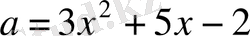 .
.
Жанасу нүктесінің абсциссасы
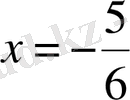 болғандықтан,
болғандықтан,
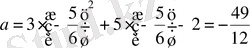 .
.
Жауабы.
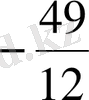 .
.
7-есеп.
 -ның қандай мәндерінде
-ның қандай мәндерінде
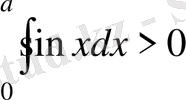 теңсіздігі орындалады?
теңсіздігі орындалады?
Шешуі.
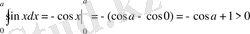 , яғни
, яғни
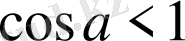 . Косинус функциясы
. Косинус функциясы
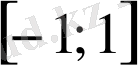 аралығынан ғана мәндер қабылдайтын болғандықтан,
аралығынан ғана мәндер қабылдайтын болғандықтан,
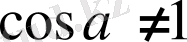 болуы жеткілікті. Бұдан
болуы жеткілікті. Бұдан
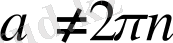 ,
,
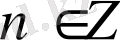 .
.
Жауабы.
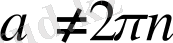 ,
,
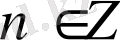 .
.
8-есеп.
 -ның қандай мәндерінде
-ның қандай мәндерінде
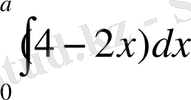 интегралының мәні 3-тен аспайды?
интегралының мәні 3-тен аспайды?
Шешуі.
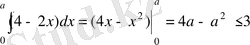

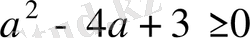 .
.
Соңғы квадраттық теңсіздікті шешіп, есептің жауабын аламыз:
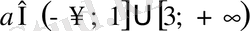 .
.
Жауабы.
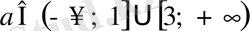 .
.
Қолданылған әдебиеттер тізімі
1. Математика - 2005 // Математика пәні бойынша оқу-әдістемелік құрал. - Астана: «Ұлттық тестілеу орталығы» РМҚК, 2005. - 256 б.
2.
Математика - 2012 // Математика пәні бойынша оқу-әдістемелік құрал. - Астана: «Ұлттық тестілеу орталығы» РМҚК, 2012. - 134 б.
3.
Математика - 2015 // Математика пәні бойынша оқу-әдістемелік құрал. - Астана: «Ұлттық тестілеу орталығы» РМҚК, 2015. - 124 б.
4. Альсейтов А. Г. Математика талапкерге: Ұлттық Бірыңғай Тестілеуге дайындалуға арналған тест нұсқалары. - Орал. - Полиграфсервис. 2012. - 220 б.
5. Альсейтов А. Г. Математика: Формулалар жинағы (анықтамалық материалдар) . - Орал. - Полиграфсервис. 2012. - 156 б.
6. Альсейтов А. Г. Математикадан қиындығы жоғары есептер. «Математика және логика». №6, 2012. 12-14 бет.
7. Альсейтов А. Г. Математика: Ұлттық бірыңғай тестілеу емтихандарында кездесетін күрделілігі жоғары, таңдамалы және «стандартты емес» есептер. - Орал. - Полиграфсервис. 2013. - 332 бет.
8. Альсейтов А. Г. Математика. 1-бөлім: Арифметика. Алгебралық теңдеулер. - Орал. - Полиграфсервис. 2013. - 212 бет.
9. Альсейтов А. Г. Математика. 4-бөлім: Функциялар. Туынды. Интеграл. - Орал. - Полиграфсервис. 2013. - 220 бет.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz