Қозғалысқа байланысты мәтін есептер

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Қозғалысқа байланысты мәтін есептер

Жоспар

Кіріспе . . . 2

1. Теңдеулер мен теңдеулер жүйелерін құруға берілген есептер (мәтін есептер) . . 3

2. Қозғалысқа байланысты есептер . . . 5

3. Қозғалысқа байланысты есептерді шешу жоспары . . . 6

4. Қозғалысқа байланысты есептердің негізгі түрлері . . . 8

4. 1. Бір пункттен екінші пунктке қарай бір бағытта қозғалыс . . . 8

4. 2. Екі пункттен бір-біріне қарама-қарсы бағытта қозғалыс . . . 9

4. 3. Бір пункттен екінші пунктке қарай жолда кідірісі бар қозғалыс . . . 10

4. 4. Су жолымен қозғалыс . . . 11

4. 5. Шеңбер бойымен қозғалыс . . . 12

Қолданылған әдебиеттер тізімі . . . 14

Кіріспе

Математика пәнінен ұлттық бірыңғай тестілеуде талапкерлер үшін қиындық туғызатын есептер қатарына теңдеулер мен теңдеулер жүйелерін құруға арналған есептер, қысқаша айтқанда, мәтін есептер жатады. Бұл түрдегі есептерді шешу үшін алдымен есептің түрін анықтап алып, содан кейін есеп шығару үшін қолданылатын формуланы (формулаларды) немесе ережені таңдап алу керек. Содан кейін ғана есептің берілгендерін пайдалана отырып, теңдеу немесе теңдеулер жүйесін құрады. Мұндай есептер негізінен сызықты теңдеуге немесе олардың жүйелеріне, квадраттық теңдеу немесе олардың жүйелеріне, сызықтық және квадраттық теңдеулердің жүйелеріне келтіріледі. Бұл тақырыпқа арналған есептерді шешу, шын мәнінде, белгілі бір дәрежеде ұзақ процесс болып табылады: есептің берілгендеріне (шарттарына) сәйкес тәуелсіз және тәуелді айнымалыларды белгілеп алу, оларды байланыстыратын теңдеу немесе теңдеулер жүйелерін құру және оларды шешу.

Осы мақалада мәтін есептердің ішінен қозғалысқа қатысты есептерді, олардың негізгі түрлерін және олардың әрқайсысына сәйкес есептерді шығару үлгілері келтіріледі.

1. Теңдеулер мен теңдеулер жүйелерін құруға берілген есептер (мәтін есептер)

Кез келген мәтін есепті шешу негізгі үш мәселеден тұрады:

1) Белгісіздерді дұрыс таңдап алу.

2) Теңдеуді, теңсіздікті немесе олардың жүйесін құру және нені табу қажеттігін анықтау.

3) Алынған теңдеуді (теңсіздікті) немесе олардың жүйесін шешу.

Сонымен қатар мәтін есептердің негізгі түрлерін айыра білу мен олардың ішіндегі ең қарапайымдарын шығара білу үлкен рөл атқарады.

Еліміздің жоғары оқу орындарына қабылдау емтихандарында мәтін есептер де кездеседі. Сондықтан мұндай есептердің негізгі түрлері мен оларды шығару жолдарын қарастырған жөн.

Қазақстан Республикасы Білім және ғылым министрлігінің Білім беру мен тестілеудің мемлекеттік стандарттарының ұлттық орталығы (БТМСҰО) 1999-2014 жылдар аралығында ұсынған тест жинақтарындағы мәтін есептерді шартты түрде келесі түрлерге бөлуге болады (жақшаның ішінде 1-ші қолданылған әдебиеттегі мәтін есептердің осы түрге жататындарының нөмірлері келтірілген) :

- қозғалыс (684, 686, 687, 690, 691, 694, 695, 697, 698, 703, 704, 711, 716, 717, 724, 731, 732, 743, 744, 747, 748, 762, 767, 769, 783, 784, 785, 786) ;

- бірлесіп жұмыс жасау (734, 741, 765, 787, 791, 807) ;

- жоспарлау және еңбек өнімділігі (688, 693, 730, 788, 805, 806) ;

- пайыздар (проценттер ) (685, 702, 707, 712, 713, 714, 715, 719, 720, 721, 723, 728, 733, 735, 742, 756, 757, 758, 759, 764, 772, 773, 774, 775, 776, 777, 778, 792, 795, 796, 797, 798, 799, 802, 808, 811, 812) ;

- құймалар мен қоспалар (725, 800, 801) ;

- арифметикалық амалдардың компоненттерінің арасындағы байланыс (689, 692, 696, 699, 700, 701, 705, 706, 708, 709, 710, 718, 722, 726, 727, 729, 736, 737, 738, 739, 740, 745, 746, 749, 750, 751, 752, 753, 754, 755, 760, 761, 763, 766, 768, 770, 771, 779, 780, 781, 782, 789, 790, 793, 794, 803, 804, 809, 810) .

2. Қозғалысқа байланысты есептер

Бұл түрдегі есептердің негізгі компоненттері:

а) жүрілген жол (

\[\begin{array}{l}{{\mathcal{C}}}\\ {{\mathsf{A}}}\end{array}\]

) ;

б) жылдамдық ( ) ;

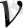в) уақыт (

\[\underline{{\land}}\]

) .

Бұл шамалардың арасындағы байланыс келесі формулалармен өрнектеледі:

\[\scriptstyle S=y\]

;

\[\nu=\frac{S}{t}\]

;

\[t={\frac{S}{v}}\]

; (1)

және бұл шамалар бір бірлік жүйесінде болулары керек; мысалы, егер жол километр -мен, ал уақыт сағат -пен есептелетін болса, онда жылдамдық км/сағ -пен есептеледі.

3. Қозғалысқа байланысты есептерді шешу жоспары

1. Есеп шарты бойынша белгісіз болатын бір шаманы таңдап алып, оны x , y немесе z және т. с. с., арқылы белгілейді.

2. Қай шама есеп шарты бойынша белгілі екендігін анықтайды.

3. Үшінші (қалған) шаманы (1) формулалардың бірінің көмегімен белгісіз ( x ) және белгілі шамалар арқылы өрнектейді.

4. Есептің шартын ескере отырып, үшінші шаманың қалай өзгеретіндігін (өседі, кемиді және т. с. с. ) көрсететін теңдеу құрады.

Егер арнайы айтылмаған болса, онда қозғалысты бірқалыпты деп есептейміз.

Қозғалыстың басқа режиміне көшудің және бағыттың өзгеруінің кез келгені лезде ( орысша: мгновенно) болады деп есептейміз.

Егер екі дене қозғалысты бір мезгілде бастайтын болса, онда олар кездесетін жағдайда, екі дене қозғалыс басталғаннан кездескенге дейін бірдей уақыт жұмсайды. Бір дене екінші денені қуып жететін жағдайда да тап солай болады.

Егер екі дене қозғалысты әртүрлі уақытта бастайтын болса, онда олар кездескенге дейін қозғалысты алғашқы бастағаны көбірек уақыт жұмсайды.

Өзен бойымен қозғалысқа қатысты есептерде келесі формулаларды

қолданған дұрыс:

\[\nu_{a.a.}=\nu+\nu\]

;

\[\nu_{a.e.}=\nu-\nu\]

;

\[\nu=\frac{\nu_{a\,\bar{d}\circ}+\nu_{a\,\bar{s}_{*}}}{2}\]

мұндағы

\[\nu_{a,{\bar{a}}}.\]

- ағыс бағытымен жылдамдық,

\[\nu_{a,\theta}.\]

- ағысқа қарсы жылдамдық,

\[\downarrow\rangle\]

- қайықтың меншікті жылдамдығы,

\[\mathbf{}W\]

- ағыстың жылдамдығы.

Екі дененің шеңбер бойымен

\[{\mathcal{V}}_{1}\]

және

\[\nu_{2}\]

(

\[\nu_{1}>\nu_{2}\]

) тұрақты жылдамдықтарымен қозғалысы кезінде олардың кездесулерінің арасындағы уақыт келесі формулалармен есептеледі:

а) егер екі дене бір бағытта қозғалса, онда:

\[\frac{\phi\hat{a}l\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}\hat{a}}{\nu_{1}-\nu_{2}}\]

;

ә) егер екі дене қарама-қарсы бағытта қозғалса, онда:

\[\frac{\phi\tilde{d}l\tilde{a}\tilde{a}\tilde{a}\tilde{\partial}}{\nu_{1}+\nu_{2}}\]

4. Қозғалысқа байланысты есептердің негізгі түрлері

1) Бір пункттен екінші пунктке қарай бір бағытта қозғалыс.

2) Екі пункттен бір-біріне қарама-қарсы бағытта қозғалыс.

3) Бір пункттен екінші пунктке қарай жолда кідірісі бар қозғалыс.

4) Су жолымен қозғалыс.

5) Шеңбер бойымен қозғалыс.

Енді осы қозғалысқа байланысты мәтін есептердің негізгі түрлеріне мысалдар ретінде есептердің толық шығару жолдарын келтіреміз.

4. 1. Бір пункттен екінші пунктке қарай бір бағытта қозғалыс

Мысал. Ара қашықтығы 18 км-ге тең А пунктінен В пунктіне қарай жаяу жолаушы шықты. Оның артынан 2 сағаттан кейін, әр сағат сайын жаяу жолаушыға қарағанда 4, 5 км-ге артық жол жүретін велосипедші шықты. Егер В пунктіне жаяу жолаушы мен велосипедші бір уақытта жеткені белгілі болса, онда велосипедшінің жылдамдығын табу керек.

Шешуі. v - велосипедшінің жылдамдығы. Есеп шартынан оның жұмсайтын уақыты

\[\frac{18}{\nu}\]

(себебі S = v ∙ t ), жаяу адамның жұмсайтын уақыты

\[\frac{18}{\nu-4.5}\]

екендігі шығады. Сондықтан, есеп шарттарын ескере отырып, келесі теңдеуді аламыз:

\[\frac{18}{\nu-4.5}\]

\[\frac{18}{\nu}\]

\[=2\]

; және оны түрлендіріп,

\[{\mathcal{D}}\nu^{2}\,_{=}\ \Theta\nu\,_{+}\ \mathcal{\otimes}1\equiv\emptyset\]

квадраттық теңдеуін аламыз. Оның түбірлері

\[\nu_{1}=9\]

\[\nu_{2}=-\lambda_{5}.\]

. Сонымен, есептің жауабы

\[\scriptstyle\nu=9\]

км/сағ, себебі жылдамдық теріс бола алмайды.

Жауабы.

\[\scriptstyle\nu=9\]

км/сағ.

4. 2. Екі пункттен бір-біріне қарама-қарсы бағытта қозғалыс

1-мысал. Ара қашықтығы 500 км екі қаладан бір мезгілде қарама-қарсы бағытта трактор мен одан жылдамдығы 4 есе артық жүк машинасы шығып, 4 сағаттан кейін кездесті. Трактор жылдамдығы қандай?

Шешуі. v - трактордың жылдамдығы. Есеп шартынан жүк машинасының жылдамдығы

\[{\mathrm{d}}\nu\]

және

\[(\nu+4\nu)\chi\lambda=500\]

, себебі екі көлік бір мезгілде шыққандықтан, олар жолды бірлесіп жүріп өтеді. Соңғы теңдеуден

\[5v=125\]

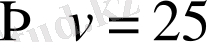км/сағ.

Жауабы.

\[\nu=25\]

км/сағ.

2-мысал. Сағатына 70 км/сағ жол жүретін жүрдек поезд С станциясынан D станциясына қарай шықты, ал 1 сағ өткеннен кейін оған қарама-қарсы D станциясынан сағатына 45 км/сағ жол жүретін жүк поезы шықты. Егер CD темір жол бөлігінің ұзындығы 530 км болса, онда осы екі поезд бірімен-бірі D станциясынан қандай қашықтықта кездесер еді?

Шешуі. 1-ші сағатта жүрдек поезд 70 км жүреді, қалған 530 - 70 =460 км жолды екі поезд

\[\frac{460}{70+45}=\frac{460}{115}=4\]

сағатта жүріп өтеді, яғни жүк поезы кездескенге дейін 4 сағат жүреді. Олай болса, жүк поезы кездескенге дейін 45 ∙ 4 = 180 км жол жүреді.

Жауабы. 180 км.

3-мысал. Бір мезгілде А және В пункттерінен бір-біріне қарама-қарсы бағытта жолға шыққан екі велосипедші 2 сағ-тан кейін жолықты. А-дан В-ға дейінгі қашықтық 42 км-ге тең. Егер бірінші велосипедші сағатына екіншісіне қарағында 3 км жолды артық жүріп отырса, онда олардың әрқайсысының жылдамдығының қандай болғаны?

Шешуі. 1-ші және 2-ші велосипедшілердің жылдамдықтарын сәйкесінше x және y деп белгілейік. Есеп шарттарынан келесі жүйені аламыз:

\[\textstyle{\frac{1}{k}}\,=\,y+1,\]

\[\textrm{l i}_{[2y+3=21}\]

\[\mathrm{P}\ \ y=9,\ \ \ x=12\]

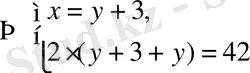
Жауабы. 12 км/сағ, 9 км/сағ.

4. 3. Бір пункттен екінші пунктке қарай жолда кідірісі бар қозғалыс

1-мысал. Поезд жолда 6 мин-қа тоқталды да, өзінің кешігуін 20 км-лік жол кесіндісінде жойды. Ол үшін поездың қозғалыс кестесі бойынша жорамалдаған жылдамдығынан 10 км/сағ артық жылдамдықпен жүруіне тура келді. Берілген жол кесіндісіндегі поездың кесте бойынша жорамалданған жылдамдығын табыңыздар.

Шешуі. 6 минут

\[={\frac{1}{10}}\]

сағат. Есеп шарты бойынша

\[{\frac{20}{\nu+10}}+{\frac{1}{10}}={\frac{20}{\nu}}\]

\[\mathbf{\mathcal{D}}\]

\[{\frac{200+\nu+10}{10\nu+100}}={\frac{20}{\nu}}\]

\[\nu^{2}+10\nu-2000=0\]

. Соңғы квадраттық теңдеудің түбірлері:

\[\nu=40\]

км/сағ,

\[\nu=-50\]

- бөгде түбір, себебі жылдамдық - теріс емес шама.

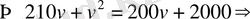
Жауабы.

\[\nu=40\]

км/сағ.

2-мысал. Шаңғышының 30 км-лік ара қашықтығы жүгіріп өтуі тиіс еді. Жүгіруді белгілеген уақытынан 3 мин кешірек бастаған шаңғышы жоспарланған жылдамдықтан 1 км/сағ артық жылдамдықпен жүгіріп отырып, белгіленген жерге дер кезінде келіп жетті. Шаңғышы қандай жылдамдықпен жүгірді?

Шешуі. Шаңғышының жүгірген жылдамдығы v болсын, сонда оның бастапқы жүгіруге тиісті жылдамдығы

\[\nu-\hat{\Lambda}\]

болады. 3 минут=0, 05 сағат екенін ескере отырып, есеп шартына сәйкес теңдеу құрамыз:

\[{\frac{30}{\nu-1}}-{\frac{30}{\nu}}\!=\!0{\mathrm{,}}\!05\]

. Бұдан

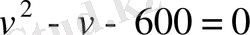квадрат теңдеуі шығады. Оны шешіп,

\[\nu_{1}=\mathcal{D}\]

\[\nu_{2}=-24\]

түбірлерін аламыз. Жылдамдық теріс бола алмайтынын ескерсек,

\[\nu=25\]

км/сағ екендігі шығады.

Жауабы.

\[\nu=25\]

км/сағ.

4. 4. Су жолымен қозғалыс

1-мысал. Қайықшы 16 км қашықтықты өзеннің ағысы бойымен, ағысқа қарсы жүруге кеткен уақытқа қарағанда 6 сағатқа тезірек жүріп өтеді; сонымен қатар ағынсыз судағы қайықтың жылдамдығы өзен ағысы жылдамдығынан 2 км/сағ-қа артық. Қайықтың тынық судағы жылдамдығын және өзен ағысының жылдамдығын табу керек.

Шешуі. v , w - сәйкесінше қайықтың және ағыстың жылдамдықтары.

Есеп шартынан

\[\nu=\,w+2\]

\[{\frac{16}{\nu+w}}={\frac{16}{\nu-w}}-6\]

. Екінші теңдеуге бірінші теңдеуден v -ның мәнін қойсақ:

\[{\frac{16}{2w+2}}={\frac{16}{2}}-6\]

немесе

\[{\frac{16}{2w+2}}=2\]

, яғни

\[\scriptstyle w=3\]

км/сағ, және

\[\nu=\,w+2\]

болғандықтан,

\[\nu=5\]

км/сағ болады.

Жауабы.

\[\scriptstyle w=3\]

км/сағ,

\[\nu=5\]

км/сағ.

2-мысал. Моторлы қайық ағынсыз суда 54 км жолды жүруге кететін уақытта өзен ағысымен 28 км, ағынға қарсы 25 км жол жүрді. Егер өзен ағысы жылдамдығы 2 км/сағ болса, онда қайықтың ағынсыз судағы жылдамдығын анықтау керек.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.