Теңдеулер мен олардың жүйелерін құруға арналған күрделі мәтін есептері: классификациясы және шешімдері


Күрделі мәтін есептер
Жоспар
Кіріспе . . . 2
Теңдеулер мен олардың жүйелерін құруға берілген есептер
(мәтін есептер) классификациясы . . . 3
Есептер шығару . . . 4
Қолданылған әдебиеттер тізімі . . . 11
Кіріспе
Мектеп математика курсында, соның ішінде Ұлттық бірыңғай тестілеуде математика пәнінен талапкерлерге ұсынылатын есептердің ішінде теңдеулер мен олардың жүйелерін құруға берілген есептер, қысқаша айтқанда, мәтін есептер ерекше орын алады. Себебі мәтін есептер, біріншіден өмірге жақын, дәлірек айтқанда өмірде болып жатқан құбылыстар мен іс-әрекеттерге байланысты болады, екіншіден, ол теңдеулерді құру үлкен сауаттылықты талап етеді (өйткені, мәтін есептер негізінен физикалық құбылыстарды бейнелейді) . ҰБТ-да ұсынылып жүрген есептердің ішінде қиын, күрделілігі жоғары, тіпті олимпиадалық сипаттағы есептер де кездеседі (мысалы, 7-есеп) .
Бұл мақалада математика пәнінен ҰБТ-да талапкерлерге ұсынылып жүрген мәтін есептер ішіндегі күрделірек деген бірнеше есепті толық шешулерімен келтіреміз. Мақала соңындағы қолданылған әдебиеттер тізімінен автордың талапкерге осы тақырыпқа қатысты қосымша оқу үшін ұсынатын еңбектерін көруге болады. Мәтін есептер мен олардың түрлері және олардың әрбір түрін шешудің тәсілдерімен толығырақ қолданылған әдебиеттер тізіміндегі 8-кітаптан танысуға болады.
Теңдеулер мен олардың жүйелерін құруға берілген есептер (мәтін есептер) классификациясы
Еліміздің жоғары оқу орындарына қабылдау емтихандарында мәтін есептер де кездеседі. Сондықтан мұндай есептердің негізгі түрлері мен оларды шығару жолдарын қарастырған жөн.
Қазақстан Республикасы Білім және ғылым министрлігінің Білім беру мен тестілеудің мемлекеттік стандарттарының ұлттық орталығы (БТМСҰО) 1999-2014 жылдар аралығында ұсынған тест жинақтарындағы мәтін есептерді шартты түрде келесі түрлерге бөлуге болады (жақшаның ішінде 1-ші қолданылған әдебиеттегі мәтін есептердің осы түрге жататындарының нөмірлері келтірілген) :
- қозғалыс (684, 686, 687, 690, 691, 694, 695, 697, 698, 703, 704, 711, 716, 717, 724, 731, 732, 743, 744, 747, 748, 762, 767, 769, 783, 784, 785, 786) ;
- бірлесіп жұмыс жасау (734, 741, 765, 787, 791, 807) ;
- жоспарлау және еңбек өнімділігі (688, 693, 730, 788, 805, 806) ;
- проценттер (685, 702, 707, 712, 713, 714, 715, 719, 720, 721, 723, 728, 733, 735, 742, 756, 757, 758, 759, 764, 772, 773, 774, 775, 776, 777, 778, 792, 795, 796, 797, 798, 799, 802, 808, 811, 812) ;
- құймалар мен қоспалар (725, 800, 801) ;
- арифметикалық амалдардың компоненттерінің арасындағы байланыс (689, 692, 696, 699, 700, 701, 705, 706, 708, 709, 710, 718, 722, 726, 727, 729, 736, 737, 738, 739, 740, 745, 746, 749, 750, 751, 752, 753, 754, 755, 760, 761, 763, 766, 768, 770, 771, 779, 780, 781, 782, 789, 790, 793, 794, 803, 804, 809, 810) .
Есептер шығару
1-есеп. Турист өзен ағысымен 90 км-ді қайықпен жүзді де, қалған 10 км-ді жаяу жүріп өтті. Оның жаяу жүріп өткен уақыты, қайықпен жүзуге кеткен уақытынан 4 сағатқа кем еді. Егер турист қайықпен жүзіп өткен уақытындай жаяу жүрсе, ал жаяу жүріп өткен уақытындай қайықпен жүзсе, онда олардың жүрген жолдары бір-біріне тең болар еді. Турист қанша уақыт жаяу жүрді және қанша уақыт қайықпен жүзіп өтті?
Шешуі.
Турист
x
сағат жаяу жүрген,
у
сағат қайықпен жүзген болсын. Онда
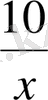 - жаяу жүргендегі жылдамдығы,
- жаяу жүргендегі жылдамдығы,
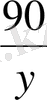 - қайықпен жүзгендегі жылдамдығы. Есеп шарты бойынша
- қайықпен жүзгендегі жылдамдығы. Есеп шарты бойынша
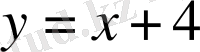 және
және
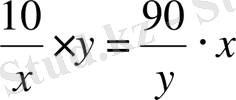 . Екінші теңдеуден
. Екінші теңдеуден
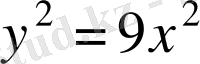 немесе
немесе
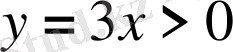 , себебі уақыт теріс емес шама.
, себебі уақыт теріс емес шама.
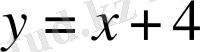 және
және
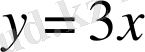 теңдеулерінен
теңдеулерінен
 ,
,
 .
.
Жауабы.
 сағ,
сағ,
 сағ.
сағ.
1-есеп. Катер өзен ағысымен 75 км және ағысқа қарсы 75 км жүрді. Катер барлық жолға тынық суда 80 км жүретін уақыттан 2 есе артық жұмсады. Егер ағынның жылдамдығы 5 км/сағ болса, катердің жылдамдығы неге тең?
Шешуі. v , w - сәйкесінше катердің және ағыстың жылдамдықтары.
Есеп шарттарынан
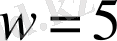 км/сағ,
км/сағ,
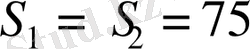 км, және келесі жүйені аламыз:
км, және келесі жүйені аламыз:
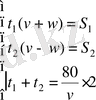 .
.
Жүйенің алғашқы екі теңдеуін мүшелеп қоссақ және азайтсақ, келесі теңдеулер жүйесін аламыз:
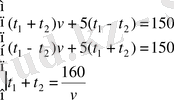 .
.
Жүйенің үшінші теңдеуінен
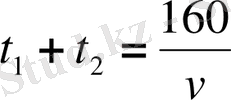 мәнін алғашқы екі теңдеуге қойсақ:
мәнін алғашқы екі теңдеуге қойсақ:
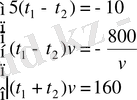 және соңғы жүйенің бірінші теңдеуінен
және соңғы жүйенің бірінші теңдеуінен
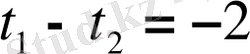 болғандықтан, екінші теңдеуі
болғандықтан, екінші теңдеуі
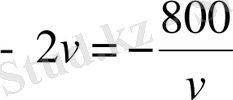 түрін қабылдайды, бұдан
түрін қабылдайды, бұдан
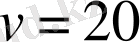 км/сағ.
км/сағ.
Жауабы.
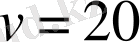 км/сағ.
км/сағ.
3-есеп. Өзен жағасында орналасқан А және В пункттерінің ара қашықтығы 10 км. А пунктінен шыққан қайық өзен ағысының бойымен жүзіп В пунктіне келді де, кідірместен кері қайтты. Егер қайықтың тынық судағы жылдамдығы 3 км/сағ болса, онда А-дан В-ға жету үшін В-дан А-ға жетуге кеткен уақыттан 2 сағ 30 мин кем уақыт жұмсалар еді. А пунктінен В пунктіне 2 сағатта жету үшін қайықтың тынық судағы жылдамдығының қандай болуы қажет?
Шешуі.
v
,
w
- сәйкесінше қайықтың және ағыстың жылдамдықтары. Есеп шарттарынан келесі теңдеуді аламыз:
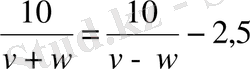 . Шарт бойынша
. Шарт бойынша
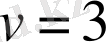 болғандықтан, теңдеу
болғандықтан, теңдеу
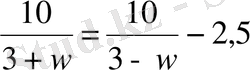 түріне келеді. Оны түрлендіріп,
түріне келеді. Оны түрлендіріп,
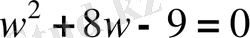 квадраттық теңдеуін аламыз. Оның түбірлері
квадраттық теңдеуін аламыз. Оның түбірлері
 ,
,
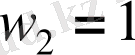 . Жылдамдық теріс бола алмайтындықтан:
. Жылдамдық теріс бола алмайтындықтан:
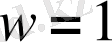 км/сағ. Ара қашықтығы 10 км болатын А пунктінен В пунктіне қайық өзен ағысының бойымен 2 сағатта жету үшін қайықтың тынық судағы жылдамдығы
км/сағ. Ара қашықтығы 10 км болатын А пунктінен В пунктіне қайық өзен ағысының бойымен 2 сағатта жету үшін қайықтың тынық судағы жылдамдығы
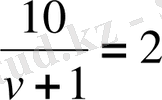 теңдеуін қанағаттандыруы керек, оның түбірі
теңдеуін қанағаттандыруы керек, оның түбірі
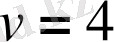 км/сағ.
км/сағ.
Жауабы. 4 км/сағ.
4-есеп. Сағат тілдері секіріссіз қозғалады деп есептесек, сағат 4-ті көрсеткеннен кейін, қанша уақытта минуттық тіл сағаттық тілді бірінші рет қуып жетеді?
Шешуі.
Минуттық тіл минутына
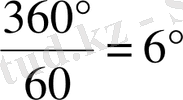 градусқа бұрылады; ал сағаттық тіл минуттық тілден 12 есе баяу қозғалатын болғандықтан (себебі сағаттық тіл дөңгелекті бір айналғанда минуттық тіл дөңгелекті 12 рет айналады) минутына
градусқа бұрылады; ал сағаттық тіл минуттық тілден 12 есе баяу қозғалатын болғандықтан (себебі сағаттық тіл дөңгелекті бір айналғанда минуттық тіл дөңгелекті 12 рет айналады) минутына
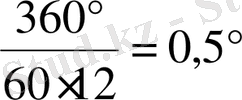 градусқа бұрылады. Сонда 1 минутта минуттық тіл мен сағаттық тіл арасындағы 120°-тық айырмашылық (қашықтық) 6° - 0, 5°=5, 5° -қа қысқарады. 120°-тық айырмашылықты жою үшін, яғни минуттық тіл сағаттық тілді бірінші рет қуып жетуі үшін
градусқа бұрылады. Сонда 1 минутта минуттық тіл мен сағаттық тіл арасындағы 120°-тық айырмашылық (қашықтық) 6° - 0, 5°=5, 5° -қа қысқарады. 120°-тық айырмашылықты жою үшін, яғни минуттық тіл сағаттық тілді бірінші рет қуып жетуі үшін
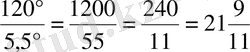 минут қажет.
минут қажет.
IV
XII
120°
O
Жауабы.
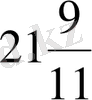 минут.
минут.
5-есеп. Қозғалып тұрған эскалатормен бала 30 секундта жүгіріп түседі, ал қозғалмай тұрған эскалатормен 45 секундта жүгіріп түседі. Эскалатордың өзі қанша уақытта түседі?
Шешуі
.
Жүрілетін жолды 1 деп алуға болады. Қозғалып тұрған эскалатормен бала қозғалмай тұрған эскалатормен түскенге қарағанда тез түсетін болғандықтан, бала мен эскалатордың қозғалыс бағыттары бірдей деген сөз; сондықтан баланың қозғалып тұрған эскалатормен түскендегі жылдамдығы оның қозғалмай тұрған эскалатормен түскендегі жылдамдығы мен эскалатор жылдамдығының қосындысына тең (өзен ағысы бағытымен қозғалысқа ұқсас), яғни:
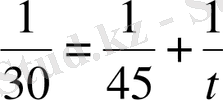 . Бұдан
. Бұдан
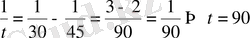 секунд.
секунд.
Жауабы . 90 секунд.
6-есеп. Үйден мектепке дейін 400 м. Жоғары сынып оқушысы төменгі сынып оқушысына қарағанда бұл жолға 300 адым аз жұмсайды, себебі оның адымы төменгі сынып оқушысының адымына қарағанда 30 см үлкен. Әрбір баланың адымының ұзындығын табыңыз.
Шешуі.
Жоғары сынып оқушысының адымының ұзындығын
х
, төменгі сынып оқушысының адымының ұзындығын
у
делік. Есеп шарттарына сәйкес (1 метр=100 сантиметр)
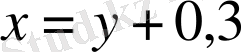 , және келесі теңдеулер жүйесін құрып, оны шешеміз:
, және келесі теңдеулер жүйесін құрып, оны шешеміз:
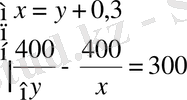 ,
,
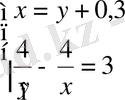 .
.
Жүйенің екінші теңдеуінен
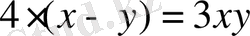 ,
,
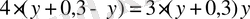 ,
,
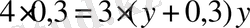 ,
,
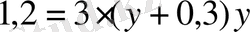 ,
,
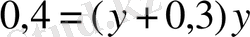 ,
,
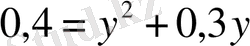 ,
,
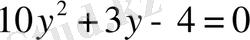 .
.
Соңғы квадраттық теңдеудің дискриминанты
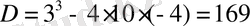 , сонда
, сонда
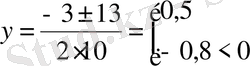 . Сонымен, төменгі сынып оқушысының адымының ұзындығы 0, 5 м, ал жоғары сынып оқушысының адымының ұзындығы
. Сонымен, төменгі сынып оқушысының адымының ұзындығы 0, 5 м, ал жоғары сынып оқушысының адымының ұзындығы
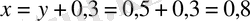 м.
м.
Жауабы. 0, 5 м және 0, 8 м.
7-есеп. Бір кесек металдың массасы 880 г, ал екіншісінікі 858 г және бірінші кесектің көлемі екіншісінен 10 см 3 кем. Біріншісінің тығыздығы екіншісінің тығыздығынан 1 г/см 3 артық. Металлдың әр кесегінің тығыздығын табыңыз.
Шешуі
.
Бірінші және екінші кесектердің көлемдерін, массаларын және тығыздықтарын сәйкесінше
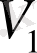 ,
,
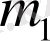 және
және
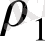 ,
,
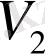 ,
,
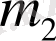 арқылы белгілейік. Көлем, масса және тығыздық арасындағы байланысты (
арқылы белгілейік. Көлем, масса және тығыздық арасындағы байланысты (
 ) және есептің берілгендерін ескере отырып, (
) және есептің берілгендерін ескере отырып, (
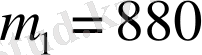 ,
,
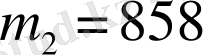 ) теңдеулер жүйесін құрамыз:
) теңдеулер жүйесін құрамыз:
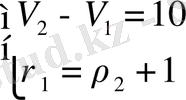 .
.
Оны түрлендіреміз:
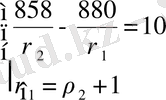 ,
,
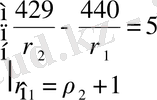 ,
,
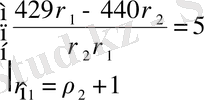 ,
,
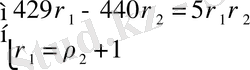 ,
,
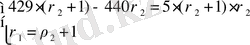 ,
,
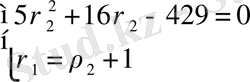 .
.
Жүйенің бірінші теңдеуін шешеміз. Оның түбірлері
 және
және
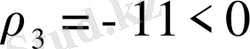 . Тығыздық оң шама болуы себепті, есептің жауабы
. Тығыздық оң шама болуы себепті, есептің жауабы
 г/см
3
және
г/см
3
және
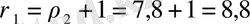 г/см
3
болады.
г/см
3
болады.
Жауабы . 8, 8 г/см 3 , 7, 8 г/см 3 .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz