Шамалар туралы мәлімет және кестелік шамаларды өңдеу алгоритмдері


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:
Мазмұны
Кіріспе3
І-ТАРАУ. ШАМА ТУРАЛЫ МӘЛІМЕТ.
1. 1Шамалар ұғымы. Шаманың типтері. …. 4
1. 2 Кестелік шамалар. Сандық алгоритмдердің кесте түріндегі
орындалуы8
ІІ-ТАРАУ. КЕСТЕЛІК ШАМАЛАРМЕН ЖҰМЫС ІСТЕУ АЛГОРИТІМІ.
2. 1 Кестклік шамаларды өндеу. 13
2. 2 Кестелік шамалар және жұмыс істеу. ……. . 18
Қорытынды. 24
Пайдалынған әдебиеттер25
Кіріспе
Шамалар - информацияны өңдеу кезінде қолданылатын объектілер. Яғни, шамаларға алғашқы деректер (алғашқы информациялар) және нәтиже деректер (өңдегеннен кейінгі информация) жатады. Бұл жағдайда информацияның хабары маманың есімі ретінде, ал информацияның мазмұны шамаңың мәні ретінде қарастырылады.
Шамалар, өздерінің есімдеріне мәндер беру тәсіліне байланысты тұрақты шама және айнымалы шама болып екіге бөлінеді.
Егер шаманың мәні қолданып отырған қатынас тілінің жалпы интерпретациялау (түсіну) ережесін құрған кезде анықталса, онд мұндай шамаларды тұрақты дейміз. Демек, тұрақты шамаға атау берген кезде оның мәні бірге анықталады. Мәнімен бірге оның тип де белгілі болады. Мысалы, 1, 3 және 5 цифрларынан құрылған 135 тізбегін тұрақты шаманың атауы деп қарастырсақ, онда бұл шаманың мәні "бір жүз отыз бес" деген бүтін сан болады. Ал осы цифрлардан басқа тізбек 315 құрастырсақ, онда ол мәні "үш жүз он бес" деген бүтін сан болатын басқа тұрақты шаманың атауы болады. Осылардан мынадай тұжырым шығады:
Тұрақты шаманың есімі, мәні және типі өзгермейді, олардың барлығы бір мезгілде анықталады.
Енді айнымалы шамаға анықтама берейік. Егер шаманың атауына берілген мән өңдеу кезінде өзгеретін ; болса, онда мұндай шаманы айнымалы шама дейміз. [1]
Әдетте, айнымалы шаманың мәнінің типі өзгермеуі тиіс. Ал олай болмаған жағдайда, осы шаманы өңдеу кезінде көп, мүмкін болатын шешуі қате шығатын, қиындықтар пайда болады.
Информатикада айнымалы шамаға атау беру үшін идентификатор деген ұғымды пайдаланады. Идентификатор - әріптен басталатын және әріптер мен цифрлардан құралған ұзындығы шектелген тізбекті айтады.
І-ТАРАУ. ШАМА ТУРАЛЫ МӘЛІМЕТ
1. 1Шамалар ұғымы. Шаманың типтері
Шаманың мәні өзінің типімен сипатталады. Жалпы, шаманың мәндерін: сандың, символдық және логикалық типтерге бөлуге болады.

Берілген шамаларды өңдеу үшін осы шамаларға амалдар қолдану керек. Ал амалдарды қолдана білу үшін олардың анықтамаларын, белгілерін және қасиеттерін білу қажет.
Амалдарды шамалардың қай типтерінде анықталғандығына айланысты сандық амалдар, символдық амалдар және логикалық амалдар деп топтастырып атауға болады.
Айта кететін бір жағдай, ол осы амалдардың қайсысы болмасын математиканың түрлі саласында анықталған және зерттелген. Мысалы, символдық амалдардың барлығы "Математикалық ингвистика" деген тілдің құрамы мен қасиеттерін зерттейтін аласында, логикалық амалдардың барлығы "Математикалық логика" істен саласында, ал сандық амалдардың барлығы математиканың басқа
салаларында (арифметика, алгебра және т. б. ) анықталады.
Әрбір шама типтерінде орындалатын амалдардың қасиеттерін тықтауға болады. Ол қасиеттер топтастырылады да, осы шамаларға байланысты аксиоматика құрайды.
Төменде қарастыратын әртүлі типті шамаларға арналған аксиоматикалардың көп ұқсастықтары бар. Олар типтері сәйкес фнектердің эквиваленттігін көрсетеді, солардың ішінде коммутативтік, ассоциативтік және дистрибутивтік заңдылықтары бар. Осындай заңдылықтар берілген күрделі өрнектерді қарапайымдап, ондағы амалдар санын қысқартады және орындалуын жеңілдетеді. Олардың практикадағы маңызы өте зор. [3]
Сандың тип сандар жиынынан және оларда анықталған амалдар юн осы амалдардың қасиеттерінен қүрылады. Олар бүтін, нақты коне комплекс сандар болып үшке бөлінеді.
Ескертпе:
Информатикада сандық шамаларды өңдеу әртүрлі сандардың септеу жүйесін қажет етуі мүмкін. Ондай жүйелердің негіздері 1, 3, 4, . . . болуы ықтимал. Олардың бір бірінен айырмашылығы тек андардың мәндерін әртүрлі әдіспен белгілеу, ал сандарда шықталған амалдардың түрі және олардың қасиеттері бірдей болады. Сондықтан төменде алдымен бізге жақсы таныс сандардың ондық (негізі 10) есептеу жүйесінде жазылуы, оларда анықталған амалдар түрі және осы амалдардың қасиеттері беріледі. Сонан кейін сандардың басқа (негіздері басқа) есептеу жүйелері қарастыралады, себебі ондық есептеу жүйесіндегі сандарға байланысты айтылғандардың барльғы басқа есептеу жүйесіндегі сандарға жарайды деугеболады. Бүтін сандар араб цифрлары арқылы кескінделеді, олардың тері мәндерінің алдына "-" таңбасы жазылады, ал оң мәндерінің алдын "+" таңбасы жазылуы мүмкін.
Мысалдар:
- - 52 - теріс бүтін сан
- 376 - оң бүтін сан
- +41 - оң бүтін сан
Нақты сандар, бейнелеу тәсіліне байланысты екі топқа бөлінеді Олар: тұрақты нүктелі нақтылар және жылжымалы нүктел нақтылар.
Тұрақты нүктелі нақтылардың бейнесі бүтін және бөлшеі бөліктерден тұрады. Бүтін бөлік бөлшек бөліктің алдында (сол жағында) орналасады және олар өзара оңдық белгісі деп аталаты " " таңбасы арқылы айырылады. Олардың мәндерінің оң немесе терістігін көрсету үшін кескіндердің алдына "+" немесе "-" таңбасы жазылады. Кескіндердің екі бөліктері де араб цифрларымен бейнеленеді. [4]
Жылжымалы нүктелі нақты сандардың кескіні мантисса, есептеу жүйенің негізі және реті деп аталатын бөліктерден тұрады. Мантиссаның да, реттің де мәндері оң немесе теріс болуы мүмкін. Оларды белгілеу үшін мәндерінің алдында "+" немесе "-" жазылады. Рет бүтін сандар сияқты, ал мантисса тұрақты нүктелі нақты сияқты бейнеленеді.
Егер М мантиссаны, р ретті, q есептеу жүйенің негізін белгілесе, пида жылжымалы нүктелі нақты сандардың кескіні мынадай белады:
Осы айтылғандарды түсіну үшін кестеде жылжымалы нүктелі иақтыларға мысалдар қарастырылған.
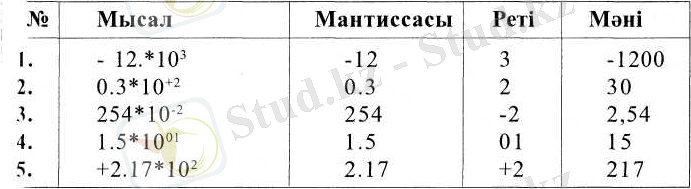
кесте. Жылжымалы нүктелі нақтыларға мысалдар
Бір ғана нақты санның жылжымалы нүктелі түрде көптеген жазылуы болуы мүмкін. Мысалы, бір ғана 3. 14 деген санның мынадай жазылулары болады:

Комплексті сандардың кескіні алгебралық қосынды түрінде беріледі. Оның бірінші қосылғышы (сол жақтағы) нақты бөлік, ал екіншісі жорамал бөлік деп аталады. Оларды бір-бірінен айыру үшін жорамал бөліктен кейін оның белгісі ретінде "і" әрпі жазылады. Нақты бөлік те, жорамал бөлік те нақты сандар түрінде жазылады.

1. 2 Кестелік шамалар. Сандық алгоритмдердің кесте түріндегі
орындалуы
Көрнекілік-материалдың түсінікті болуының алты шарттарының бірі екені белгілі:Сандық алгоритмдердің атқарылу процесі-көрнекілікті қажет ететін материалдардың бірі.
А. П. Ершов бастаған, зерттеушілер тобының оқулығында сандық мәліметтермен алгоритмнің орындалу процесін көрнекі. бейнелеуге мүмкіндік беретін тәсіл ретінде "кестенің - атқарылуын пайдалану" қарастырылады. 'Бұл компьютер болмаған кездегі есептеу процесін көрнекілеудірудің бірден бір тәсілі, болды. Бірақ бұл тәсіл әлі де өзінің мәнін жойған жоқ. Енді А-ны В-ға бөлгендегі қаддықты табу -мысалын қарастырайық (А =17, И=5) .
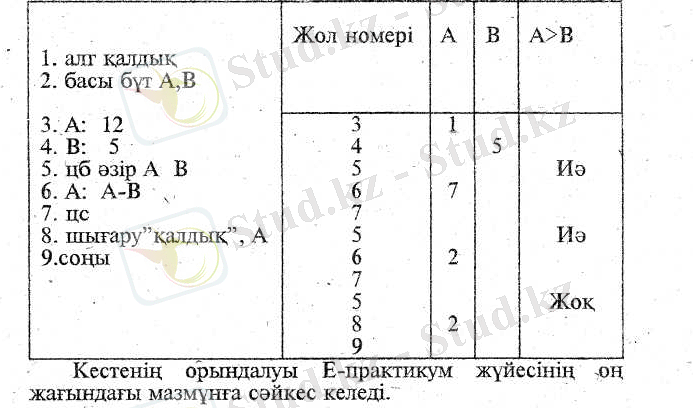
Көпшілік жағдайда оқушылардың жіберетін қатесі цикл аяқталар алдындағы соңғы цикл шартын тексермейді. Цс сөзін көргеннең кейін цикл шарты жалған екен деп циклдан шығып кетеді. Мұның себебі, әрекеттің жеткіліксіз формальдылығы болып табылады. [5]
Енді цикл құруды- қарастырайық. Егер циклды жоғарыдан төмен қарай жазылған дайын күйшде көрсетсек онда оның қалай алынғаны жұмбақ тәрізді түсініксіз күйінде қалады, Циклдың құрылу процесін төмендегідей әдіспен түсіндіруге болады. А[1:10] кестесінің мәндерінің қосындысын есептеу мысалын қарастырайық. Қадамдар мынадай тәсілмен шығарыдады. 1) Алдымен қосындының кезекті элементтің мәніне артатыны қайталанатындығын түсіндіреміз. Мысалы:
S:»S+А[1]
S:-S+А[2]
2) Осы қатынастарды жалтшлаймыз:
S:- S+ А[І]
3) Сәйксс келетін қайталану командасын тандаймыз.
Егер нәтиже орындалатын әрекеттің ретіне тәуелсіз болса, онда "үшін" циклын таңдаймыз.
- Тұжырым жасаймыз: элементтің әрбір номеріүшін қосындының мәнін элементке арттырамыз. Қайта-лану параметрі І - 1-ден 10-ға дейінгі мән кабылдайды:.
- Осы әрекетті формальды түрде жазайық:
Цб ұшін I бастап 1 дейін 10
S=S+ А[І] Цс
Кестедегі элементтср саны 10 емес, ноль болса, онда цикл бірде бір рет орындалмай, қосындының нольге тең болатынын ескертуіміз қажет. Олай болса, қосындыны есептер алдында есептегішке ноль меншіктеу қажет.
S=0
Енді командалардың пайда болу ретіже көңіл аударайық. Алдымен қайталанатьш командаларды анықтаймыз. Одан кейін ыңғайлы қайталану командасын таңдаймыз. Қайталанатын әрекеттерді жалпылаймыз, индекстің пайда болуын түсіндіреміз. Тек осы әрекеттен кейін есептегішті тазалаймыз, яғни ноль меншіктейміз.
Егер командаларды емес, жасалған талқылаудын қадамын номерлесек окушылардың дәптерге немесе тақтаға жазатын. командаларының реті төмендегідей болады: .
4 S:-о
2 Цб үшін I бастап I дейін 10
1 S:=S . [1]
3 Цс
Кестедегі ең үлкен элементті іздеу
Енді кестедегі ең -үлкен- элементті іздеу мысалын қарастырайық. Бұл алгоритм практикада өте жиі кездеседі, бірақ оның қиындығының қалай пайда болын тұрғанын, ешкім онша мән бермейді.
А[1:10] кестесі берілсін, ; А[1], А[2] элементтерінің үлкенін М[2], М[2] мен А[3] элементтернің үлкенін -М[3], . . . , . 'М[9] мен А[10] элементтерінің үлксенін М[10] арқылы белгілейік. Бүдын ортақ қатынасты шығарамнз: І>-2 болғандағы А[І] элементтерінің ішіндегі ең үлкені М[І] болып табылады. [6]
Мынадай сұрақ пайда болады: жалпы ережеге келу үшін М[1] -неге тең? Оның" алдында ешқандай элемент болмағандықтан, ол өзі үлкен элемент болып есептеледі. Сондықтан- М[1] элементі А[1] элементіне тең болады:
Енді М[1], М[2], . . . мәндерінің тізбегі. . қалай есептелетінін қарастырайық:
Егер М[1] < А[2]
ондаМ[1] =A[2]
әйтпесе М[2] := М[1]
бітті
егер М[2] :< А[3]
онда М[3] : = А[3]
әйтпесе М[3) := М[2]
бітті

Бұл формула М[І] элементінің 2-дең, 10-ға дейінгі-мән қабылдайтынын анықтайды. Мәңді индекс бойынша іріктеудің ретін біле отырып, әзір немесе үшін циклын пайдаланамыз. Енді соңғы жағдайды қарастырамыз. Формула ретімен: пайдаланынатын болса, - онда әрбір есептеуден кейін І-дің қадамың І-ге арттыру қажет: І:=І+1. Цикл денесі құрылды. Соңғы мән М[10] :болғандықтан, орындалатын амалдар үшін шарт былай; құрылады: І<=10. М[1] -элемент белгілі болғандықтан,
Тағы да жолдардың табылуретінід дәптерге немесе тақтаға жазылу реті екенін атап көрсетеміз. [7]
Енді мына мәселеге баса көңіл аудару қажет. -Мұндағы пайдаланынып отырған индекстер зердеден көп орын алатыны белгілі. Зердені үнемдеу мақсатында М-нің; иңдексін қалдырып жазуға; бола ма? Олай болса, алдымен талдап көрейік, Мысалы, М[3] элементінің
мәні М[4] -элемент есептелгеннен кешін пайдаланыла ма? Әрине, жоқ. Онда мынадай болжам енгіземіз: максимумның, барлық мәндері үшін-индекссіз бір ғана М айнымасын пайдалануға болады. Бұдан кейін барлық М-нің қасындағы жақша мен индекстерді алып
тастаймыз

ІІ-ТАРАУ. КЕСТЕЛІК ШАМАЛАРМЕН ЖҰМЫС ІСТЕУ
АЛГОРИТІМІ
2. 1 Кестклік шамаларды өндеу.
Кестелік шамалар немесе кестелер алгоритмдік шамалардың ерекше түріне жатады. Кестелер информациялардың өте үлкен массивтерімен жұмыс істеу алгоритмдерін жазу үшін пайдаланылады. Кестелік шамалар сандық немесе литерлік шамалардан тұруы мүмкін. Бұл мәндер кесте элементтері деп аталады. Сонда информацияны өңдеу процесі кестеден информацияның қажетті элементін іздеу, кестеге жаңа элементтер жазу, кестедегі элемент-тердің орналасу ретін өзгерту және тағы сол сияқты операцияларды орындауға келіп саяды.
Кестелердің ең көп тараған түрі сызықтық және тік төртбұрышты кестенің элементтері қағазға жазылған кезде тік жолға (бағанға) немесе көлденең жолға орналастырылады да, әр элемент реттік нөмірмен нөмірленеді.
Кесте элементтерінің нөмірі осы элементтің индексі деп аталады. Кестедегі қажетті элементті оның индексі бойынша іздеуге болады. Ол үшін ізделінді элементтің индексін көрсету жеткілікті. Мысалы А [6] жазуы әңгіме А сызықтық кестенің 6-шы элементі туралы болып отырғанын көрсетеді.
Қандай да болмасын бір шаманың сызықтық кесте болатынын көрсету үшін кестенің атың, элементтерінің типін және оның элементтерінің бастапқы жәйе соңғы реттік нөмірлерін көрсету жеткілікті. Алғоритмдік тілде кестенің мазмұндалуы былайша жазылады: алдымен кестеге енетін элементтердің типін көрсететін қызметші сөз (бүт, нақ, лит) және кес қызметші сезі, одан кейін кестенің аты, оған тіркес квадрат жақша ішіне кесте элементтерінің бастапқы және соңғы реттік нөмірлері қос нүктемен бөлініп жазылады. Мысалы:
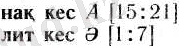
Егер кесте екі немесе одан да көп жолдан немесе бағаннан тұрса, ондай кесте тік төртбұрышты деп аталады. Тік төртбұрышты кестелер де сызықтық кестеғе ұқсас сипатталады. Тек қана тік төртбұрышты кестелерде блардың жолдарының да, бағандарының да элементтерінің бастапқы және соңғы реттік нөмірлері көрсетілуі керек. Мысалы:




2. 2 Кестелік шамалар және жұмыс істеу
ЭЕМ қуаттылығының құпиясы - жоғары жылдамдық және
үлкен көлемді зерде. Біз ЭЕМ жұмысының жылдамдығын пайдалануды үйрендік: цикл комндалары қысқа алгоритімдер құрастыруға мүмкіндік береді, Оларды ормндағанда ЭМТ үлкен тізбегін жылдам атқарады. Алайда осыған дейін біздің алгоритмдерімізді орындау барысында ЭЕМ зересінде сақталатын информация көлемі тіпті де үлкен емес еді - немесе бүтін сандар болатын. Ал, егер жүзден жүз мыңдаған сандармен жұмыс істеу қажет болса ше?Информацияның үлкен көлемімен жұмыс істейтін алгорритмдерді жазу үшін алгоритимдік тілде арнаулы кестелік шамалар(немесе кестелер) бар. [8]
Таблицалық-шамалар басқа шамалардан, элементтерден әдетте бүтің немесе нақты шамалардаң тұрады. Элементтер кестеде -әрқалай орналасуы мүмкін, бірақ ең жиі кездесетіні сызықтық кестелер .
\
Сызықтық кестелер.
Басқа кез келген шама сияқты сызықтық кесте де ЭЕМ зердесінен орын алады, оның аты және мәні болады, мысалы:

Роботтың көмегімен горизонталь дәліздегі радиациялық жағдайды зерттеу
қажет балсын, мысалы радиоактивті торкөздер
санын, радиацияның ең жоғарғы деңгейін, орташа деңгейін, қауіпті
торкөздер санын және т. б. анықтау керек болсын, Бұл есептің
шешуін екі кезеңге бөлу тиімді - информация жинау және оны
өңдеу, яғни:
І) Роботты дәлізден өткізіп, барлық торкөздердегі радиация
деңгейін есте сақтау (нақты элементті кестені пайдаланып) ;
2) ЭЕМ зердееінде сақталған информацияны өндеп, сол дәліздің қажетті сипаттамаларын есептеу (бұл кезеңде Робот қажет емес.
... жалғасы«Радиация» командасы бойынша Робот ЭЕМ-ге өзі тұрған торкөздегі радиация деңгейін хабарлайтынын еске түсірейік. Радиация деңгейін есте сақтағаннан кейін («а [і] : = радиация» комаңцасы) Робот дәліздің келесі торкөзіне кешетіндіктен («оңға» командасы) алғорнтм орындалғанда а[1] -де бірінші торкөздегі радиация деңгейі сақталады, одан кейін а [2] -де екінші торкөздеғі радмация деңгейі сақталады және т. б. Робот дәлізден шыққан кезде кестеде дәлізді радиациялық барлауға қажетті барлық информация жиналады. [9]
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz