Функцияның туындысы: теориясы, мектепте оқыту әдістемесі және қолданылуы


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 47 бет
Таңдаулыға:
Мазмұны
Кіріспе . . . . . . 3
I тарау. Функцияның туындысы . . . 6
1. 1 Функцияның туындысы деген не? . . . 6
1. 2 Функцияның туындысы ұғымына алып келетін есептер . . . 16
1. 3 Дифференциалдау ережелері . . . 16
1. 4 Функцияның дифференциалы . . . 20
1. 5 Лагранж теоремасы . . . 26
1. 6 Жоғарғы ретті туындылар . . . 26
II тарау. Функция туындысы ұғымын мектепте оқыту . . . 28
2. 1 Функция туындысы ұғымын жалпы орта білім беретін
мектеп бағдарламасына енгізудің қажеттілігі . . . 28
2. 2 Оқушыларға функция туындысы ұғымын үйрету тәсілі . . . 29
2. 3 Күрделі функцияның туындысы . . . 32
2. 4 Кері функцияның туындысы . . . 32
III тарау. Туындының мектеп математика курсында қолданылулары . . . 34
3. 1 Туындының геометриялық қолданылулары . . . 34
3. 2 Туындының механикалық қолданылулары . . . 35
3. 3 Функцияның нүктеде және аралықта өсуі мен кемуі . . . 35
3. 4 Функцияның экстремумдары . . . 36
3. 5 Функцияның аралықтағы ең үлкен және ең кіші мәндері . . . 38
3. 6 Функцияны дөңестікке зерттеу. Иілу нүктелері . . . 38
3. 7 Функцияны толық зерттеу және оның графигін салу . . . 39
Қорытынды . . . 44
Қолданылған әдебиеттер тізімі . . . 47
Кіріспе
Қазіргі қоғамдағы ғылым мен техниканың, әсіресе, компьютерлік техника мен технологиялардың даму деңгейі «біліммен қаруланған адам» даярлау қағидасынан «іс-әрекет жасауға үйретілген маман» даярлау қағидасына көшуді қажет етуде. Осы қажеттіліктің іс жүзіне ауысуы қазіргі педагогика ғылымы саласындағы кейбір мәселелерді шешуге мүмкіндік береді.
Математика пәнінің жаңа бағдарламасында «кез келген адам өз өмірінде кездесетін күрделі есептерді орындау: кесте, диаграмма, график түріндегі ақпаратты оқи алуы қажет» делінген.
Математикалық ұғымдардың ішіндегі ең іргелі де, негізгілерінің бірі функционалдық (функция) тәуелділік ұғымы. Бұл ұғымның басқа ұғымдардан басты ерекшелігі ― ол басқа оқу пәндерінде де жиі қолданылады. Функционалдық тәуелділік ― қоршаған ортаны оқып үйренуге негізделген математикалық модель. Осы модель арқылы дүниенің біртұтас ғылыми бейнесі оқып-игеріледі. Функционалдық тәуелділікті оқып-үйрену кезінде зерттелетін құбылыстардың мәні көрнекі түрде айқындалады, ұғымды оқушылардың меңгеруі басқа ұғымдардың дұрыс қалыптасуына тікелей әсерін тигізеді. Функциялық тәуелділіктің дербес жағдайы, яғни функцияның дербес жағдайы ― сандық тізбек. Туынды ұғымы математикалық анализдің негізгі ұғымдарының бірі және математикалық анализдің негізгі тұжырымдарының барлығы дерлік осы ұғым арқылы анықталатынын ескерсек, бұл ұғымның математикалық талдауға арналған кез келген оқулықтан ойып тұрып орын алатынына оңай көз жеткізуге болады. Ана тілімізде жарық көрген және өз мезгілінде университеттер мен педагогикалық институттардың физика, математика, механика факультеттері, жоғары білімді техникалық мамандар және экономика саласының мамандарын даярлайтын жоғары оқу орындарының студенттерінің математикалық анализ бен жоғары математика саласынан сапалы білім алуына үлкен жағдай жасаған О. Ә. Жәутіков /1/, Х. И. Ибрашев пен Ш. Т. Еркеғұлов /2/, Б. Т. Төлегенов /3/, Н. Темірғалиев /4/ сияқты математик-ғалымдардың еңбектерінде туынды тақырыбы терең қарастырылған. Жалпы орта білім беретін мектептерге арналған математика оқулықтарының ішінен Кеңес Одағы кезінен бері пайдаланылып келе жатқан А. Н. Колмогоровтың /5/, ал отандық соңғы буын оқулықтардың ішінен Ә. Н. Шыныбековтың /6/ және Қ. Д. Шойынбеков бастаған авторлық ұжымның еңбектерін /7/ атауға болады. 1935 жылы қазақтың тұңғыш жоғары математика оқулығын жазып шығарған Әлімхан Әбеуұлы Ермековтің еңбегінің «Сызықтық функция» тарауының «Түзу сызықтың бұрыштық коэффициентті теңдеуі. Сызықтық функцияның негізгі қасиеттері» параграфында сызықтық функцияның туындысы мен дифференциалы және туынды арқылы бұрыштық коэффициентті табу қарастырылған /8/.
Туындыға қатысты теориялық материалдар мен есептерді қамтитын және сәйкесінше жоғары оқу орындарында /9-15/ және жалпы орта білім беретін мектептерде қосымша ретінде және факультативтік сабақтар мен түрлі деңгейлердегі математикалық сайыс, конкурс, олимпиадаларға дайындық кезінде қолданылып жүрген /16-25/ оқулықтар мен оқу құралдарын атауға болады. Функцияның туындысы ұғымына қатысты және оның қолданылуларына байланысты ғылыми және ғылыми-әдістемелік журналдар мен газет беттерінде жарияланған /26-29/ мақалаларды атап кетеміз. Біз олардың барлығын дипломдық жұмысты орындау барысында жан-жақты талқылап, қажет материалдарды қолданып отырдық.
Жұмыстың мақсаты:
1) математикалық анализдің, жалпы математиканың іргелі ұғымдарының бірі болып табылатын шек ұғымының нақты қолданылуының ең негізгілерінің бірі болып табылатын функцияның туындысы ұғымын оқушылардың меңгеруін жетілдірудің шарттарын анықтау;
2) туындыны қолдануды меңгеру жолдарын, оны жүргізудің әдістемесін жасау.
Жұмыстың міндеті:
1) оқушыларда функцияның туындысы ұғымын қалыптастыру мен меңгертуді жүйелеу;
2) функцияның туындысының бар болуының қажетті шартын талдау;
3) функцияның туындысын оқып-үйренудің жалпы математиканы оқып-үйренгенде алатын орнын көрсету;
4) функцияның туындысын есептеудің тәсілдерін көрсету.
Зерттеу нысаны : «Алгебра және анализ бастамалары» пәнін оқып-үйренгенде оқушыларға функцияның туындысы ұғымын және туындыны қолдануды үйрету.
Ғылыми ізденіс әдісі:
- Педагогикалық, математикалық және басқа да әдістемелік әдебиеттерге, тақырыпқа байланысты ғылыми мақалаларға талдау жасау.
- Педагогикалық озық іс-тәжірибелерді жинақтау, талдау.
- Педагогикалық озық технология әдістерімен танысып, оның элементтерін пайдалану.
Ғылыми жаңалығы және алынған нәтижелер: Функцияның нүктедегі туындысы және аралықтағы туындысы ұғымдары тыңғылықты және тиянақты талданды; туындыға қатысты негізгі теоремалар мен қағидалардың тұжырымдамаларында берілген шарттардың әрқайсысының алатын орны талқыланды. Функцияның туындысы ұғымының мектеп математика курсында алатын орны және туындының мектеп математика курсы көлемінде негізгі қолданылулары толық талданды.
Дипломдық жұмыс кіріспеден, үш тараудан, қорытындыдан және 29 аталымды қамтитын қолданылған әдебиеттер тізімінен тұрады; көлемі 48 бет.
I тарау. Функцияның туындысы
1. 1 Функцияның туындысы деген не?
Шек ұғымы функциялық тәуелділік ұғымы сияқты математикалық талдаудың маңызды концепцияларының бірі. Математикалық талдауда негізгі үш амал бар, олар: қосу, көбейту және шекке көшу. Басқа амалдардың барлығы осы амалдарға туынды амалдар болып табылады. Қосу мен көбейту мектеп математика курсының негізгі амалдары болып табылатыны баршаға аян. Шек ұғымының негізгі қолдануларының бірі - туынды, дәлірек айтқанда, функцияның туындысы шекке көшу амалы арқылы анықталады. Дифференциалдау мен интегралдау ілімдері математикалық талдаудың негізгі (орталық) бөлімдері болып табылады.
Туынды туралы көптеген тұжырымдарды білеміз, соған қарамастан біз, біріншіден, оны тереңірек түсіну үшін, екіншіден, өзіміз үйренген туынды концепциясын толықтырып, тереңдетіп және кеңейту үшін бұл ұғыммен тыңғылықты және тиянақты айналысуымыз керек.
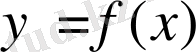
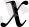 тәуелсіз айнымалысының
тәуелсіз айнымалысының
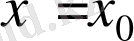 нүктесінің қандай да бір маңайында анықталған функция болсын. Егер біз
нүктесінің қандай да бір маңайында анықталған функция болсын. Егер біз
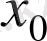 нүктесінен осы маңайға тиісті
нүктесінен осы маңайға тиісті
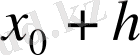 нүктесіне көшетін болсақ, онда
нүктесіне көшетін болсақ, онда
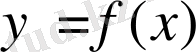 функциясы
функциясы
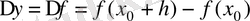 өсімшесіне ие болады, ал
өсімшесіне ие болады, ал
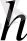 аргументтің өсімшесі
деп аталады;
аргументтің өсімшесі
деп аталады;
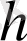 оң да, теріс те бола алатынын атап кетеміз, яғни
оң да, теріс те бола алатынын атап кетеміз, яғни
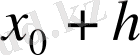 нүктесі
нүктесі
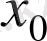 нүктесінің оң жағында да, сол жағында да жата алады. Егер біздің
нүктесінің оң жағында да, сол жағында да жата алады. Егер біздің
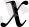 тәуелсіз айнымалысы өзгергенде
тәуелсіз айнымалысы өзгергенде
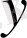 шамасы (функциясы) қаншалықты тез өзгеретіндігі жөнінде мәлімет алғымыз келсе, яғни
шамасы (функциясы) қаншалықты тез өзгеретіндігі жөнінде мәлімет алғымыз келсе, яғни
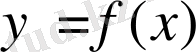 функциясы аргументтің осындай өзгерісіне қаншалықты сезімтал екендігін білгіміз келсе, онда біз, әрине, қандай да бір тәсілмен
функциясы аргументтің осындай өзгерісіне қаншалықты сезімтал екендігін білгіміз келсе, онда біз, әрине, қандай да бір тәсілмен
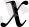 тәуелсіз айнымалысының өзгеруі мен
тәуелсіз айнымалысының өзгеруі мен
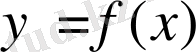 функциясының оның (
функциясының оның (
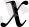 тәуелсіз айнымалысының) өзгерісі салдарынан пайда болған өсімшесін сәйкестендіріп салыстыруымыз керек. Бұл мақсатта
тәуелсіз айнымалысының) өзгерісі салдарынан пайда болған өсімшесін сәйкестендіріп салыстыруымыз керек. Бұл мақсатта
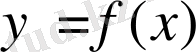 функциясының
функциясының
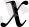 тәуелсіз айнымалысының өсімшесінің бірлігіне есептелген орташа өсімшесін беретін
тәуелсіз айнымалысының өсімшесінің бірлігіне есептелген орташа өсімшесін беретін
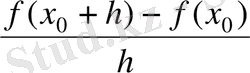 (1)
(1)
қарастырады. Бірақ бұл есептеу
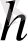 -тың нақты мәні арқылы жүргізілген болғандықтан, жалпы алғанда,
-тың нақты мәні арқылы жүргізілген болғандықтан, жалпы алғанда,
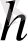 -тың әртүрлі мәндерінде әртүрлі нәтиже беретін болады. Қойылған мәселе бірмәнді шешілуі үшін
-тың әртүрлі мәндерінде әртүрлі нәтиже беретін болады. Қойылған мәселе бірмәнді шешілуі үшін
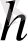 шамасын қандай да бір бірыңғай принципке негіздеп таңдап алуымыз қажет.
шамасын қандай да бір бірыңғай принципке негіздеп таңдап алуымыз қажет.
Егер мақсатымыз ретінде
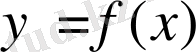 функциясының
функциясының
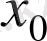 нүктесіне жақын жердегі мінезін зерттеу болатын болса, онда
нүктесіне жақын жердегі мінезін зерттеу болатын болса, онда
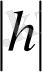 шамасын неғұрлым кішкентай етіп алсақ,
шамасын неғұрлым кішкентай етіп алсақ,
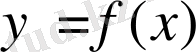 функциясының «өзгергіштік» мөлшері ретінде алған (1) шамасы біздің талабымызды соғұрлым көбірек қанағаттандыратын болады. Шын мәнінде, (1) шамасы функцияның
функциясының «өзгергіштік» мөлшері ретінде алған (1) шамасы біздің талабымызды соғұрлым көбірек қанағаттандыратын болады. Шын мәнінде, (1) шамасы функцияның
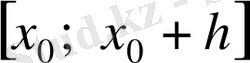 кесіндісіндегі «орташа өзгергіштігін» көрсетеді, ал ол кесінді
кесіндісіндегі «орташа өзгергіштігін» көрсетеді, ал ол кесінді
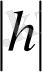 шамасы неғұрлым кіші болған сайын
шамасы неғұрлым кіші болған сайын
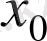 нүктесіне соғұрлым жақындай түседі. Осы пайымдаулардан кейін, шекке көшу ұғымымен таныс бізге, қойылған мәселені неғұрлым қанағаттанарлықтай етіп шешу үшін
нүктесіне соғұрлым жақындай түседі. Осы пайымдаулардан кейін, шекке көшу ұғымымен таныс бізге, қойылған мәселені неғұрлым қанағаттанарлықтай етіп шешу үшін
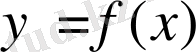 функциясының
функциясының
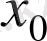 нүктесіне жақын жердегі өзгеруінің сипаттамасы ретінде (1) шамасының
нүктесіне жақын жердегі өзгеруінің сипаттамасы ретінде (1) шамасының
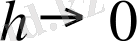 жағдайындағы шегін (бұл шек бар деп есептей отырып) қарастыру керек екендігін, яғни
жағдайындағы шегін (бұл шек бар деп есептей отырып) қарастыру керек екендігін, яғни
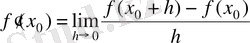 (2)
(2)
шамасын қарастыру керек екендігін түсінуімізге болады. Өзге де жалпы қабылданған белгілеулер бар:
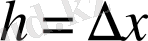 ,
,
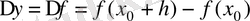 ,
,
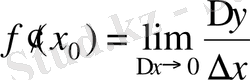 .
.
Соңғы шаманы
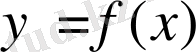 функциясының
функциясының
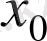 нүктесіндегі (немесе «
нүктесіндегі (немесе «
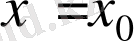 жағдайындағы») туындысы деп атайды. Сонымен, берілген функцияның берілген нүктедегі туындысы бұл функцияның берілген нүктенің оған өте жақын маңайындағы салыстырмалы өзгергіштігін сипаттайды;
жағдайындағы») туындысы деп атайды. Сонымен, берілген функцияның берілген нүктедегі туындысы бұл функцияның берілген нүктенің оған өте жақын маңайындағы салыстырмалы өзгергіштігін сипаттайды;
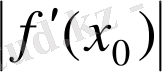 неғұрлым үлкен болған сайын
неғұрлым үлкен болған сайын
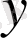 шамасы
шамасы
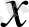 шамасының
шамасының
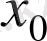 бастапқы мәнінен өте аз ауытқуының өзіне өте сезімтал болады;
бастапқы мәнінен өте аз ауытқуының өзіне өте сезімтал болады;
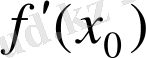 шамасының таңбасы осы өзгергіштіктің бағытын сипаттайды:
шамасының таңбасы осы өзгергіштіктің бағытын сипаттайды:
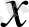 шамасының
шамасының
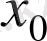 бастапқы мәнінен өте аз ауытқуының салдарынан
бастапқы мәнінен өте аз ауытқуының салдарынан
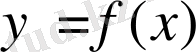 функциясының өсуі немесе кемуіне байланысты, сәйкесінше,
функциясының өсуі немесе кемуіне байланысты, сәйкесінше,
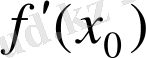 шамасы оң немесе теріс болады. Егер
шамасы оң немесе теріс болады. Егер
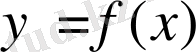 функциясын графиктік түрде бейнелейтін болсақ, яғни аталған функцияның графигін тұрғызатын болсақ, онда бізді қызықтырып отырған өзгергіштік
функциясын графиктік түрде бейнелейтін болсақ, яғни аталған функцияның графигін тұрғызатын болсақ, онда бізді қызықтырып отырған өзгергіштік
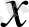 шамасы өзінің
шамасы өзінің
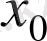 мәнінен өткенде сызылған қисық қаншалықты тік көтерілетіндігін немесе түсетіндігін бейнелейді. Дәл терминдерде туынды
мәнінен өткенде сызылған қисық қаншалықты тік көтерілетіндігін немесе түсетіндігін бейнелейді. Дәл терминдерде туынды
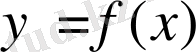 функциясының графигіне аргументі
функциясының графигіне аргументі
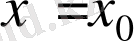 нүктесінде жүргізілген жанаманың бұрыштық коэффициенті арқылы бейнеленеді; бұл қасиетті математикада туындының геометриялық мағынасы деп атайды.
нүктесінде жүргізілген жанаманың бұрыштық коэффициенті арқылы бейнеленеді; бұл қасиетті математикада туындының геометриялық мағынасы деп атайды.
Туындының ең нақты және қарапайым түсіндірілуі
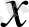 тәуелсіз айнымалысы уақытты білдірген жағдайда мүмкін болады. Бұл жағдайда (1) шамасы
тәуелсіз айнымалысы уақытты білдірген жағдайда мүмкін болады. Бұл жағдайда (1) шамасы
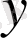 шамасының
шамасының
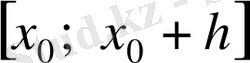 уақыт аралығындағы өзгеруінің орташа жылдамдығын білдіреді, ал
уақыт аралығындағы өзгеруінің орташа жылдамдығын білдіреді, ал
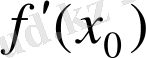 туындысы бұл өзгерістің
туындысы бұл өзгерістің
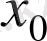 уақыт мезетіндегі «нақты жылдамдығын» білдіреді. Дербес жағдайда, егер
уақыт мезетіндегі «нақты жылдамдығын» білдіреді. Дербес жағдайда, егер
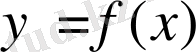 функциясы қозғалыстағы нүктенің (материалдық нүктенің) тұрақты
функциясы қозғалыстағы нүктенің (материалдық нүктенің) тұрақты
 уақыт мезетінен
уақыт мезетінен
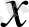 уақыт мезетіне дейін жүрген жолын білдіретін болса, онда туынды ұғымы механикадағы лездік жылдамдық ұғымымен дәл келеді, яғни бұл жағдайды функцияның нүктедегі туындысы қозғалып келе жатқан нүктенің осы нүктедегі (уақыт мезетіндегі) лездік жылдамдығына тең болады; бұл қасиетті ғылымда туындының механикалық мағынасы деп атайды.
уақыт мезетіне дейін жүрген жолын білдіретін болса, онда туынды ұғымы механикадағы лездік жылдамдық ұғымымен дәл келеді, яғни бұл жағдайды функцияның нүктедегі туындысы қозғалып келе жатқан нүктенің осы нүктедегі (уақыт мезетіндегі) лездік жылдамдығына тең болады; бұл қасиетті ғылымда туындының механикалық мағынасы деп атайды.
Зерттеліп отырған құбылыстың локальдік (жергілікті) сипаттамасын нағыз маңызды қатынаста - өзара байланыстағы екі айнымалы шаманың бірінің өзгерісі салдарынан екіншісінің өзгеруін сандық қатынаста бағалауы туындының математикалық талдаудың қолдану өрісінде: механика, астрономия, химия, биология және де жаратылыстану ғылымдарының басқа салаларында маңызды рөлге ие болуына мол мүмкіндік ашады.
Адам (оқушы) туынды ұғымын бірінші рет естігенде «неге туынды деп аталады? Әңгіме шек, сан, өсімше туралы болып отырған жоқ па?» деген сұрақтарды қоюы әбден мүмкін. «Туынды» деген сөз «функцияның туындысы» дегеннің қысқаша түрі. Барлық пайымдаулар мен есептеулер
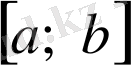 кесіндісінің (тұйық аралығының) ерікті түрде алынған (бір ғана)
кесіндісінің (тұйық аралығының) ерікті түрде алынған (бір ғана)
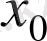 нүктесінде жүргізілгендіктен, біз осы пайымдаулар мен есептеулерді осы аралықтың кез келген
нүктесінде жүргізілгендіктен, біз осы пайымдаулар мен есептеулерді осы аралықтың кез келген
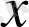 нүктесі үшін (әр жолы есептегелі отырған шек бар деп санай отырып) жүргізе аламыз. Осы тәсілмен алынған
нүктесі үшін (әр жолы есептегелі отырған шек бар деп санай отырып) жүргізе аламыз. Осы тәсілмен алынған
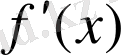 функциясы
функциясы
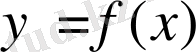 функциясының туындысы деп аталады. Бұл барлық ойқорытулар туынды функцияның тұтас
функциясының туындысы деп аталады. Бұл барлық ойқорытулар туынды функцияның тұтас
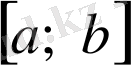 кесіндісіндегі емес, ал оның жекелеген нүктелерінің нақты өте кішкене маңайындағы мінезін сипаттауға бағытталған және берілген аралықтың әр нүктесінде ерекше есептелінетін берілген функцияның локальді (жергілікті) сипаттамасы деген негізгі фактіде ештеңе өзгертпейді.
кесіндісіндегі емес, ал оның жекелеген нүктелерінің нақты өте кішкене маңайындағы мінезін сипаттауға бағытталған және берілген аралықтың әр нүктесінде ерекше есептелінетін берілген функцияның локальді (жергілікті) сипаттамасы деген негізгі фактіде ештеңе өзгертпейді.
Егер
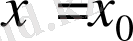 нүктесінде
нүктесінде
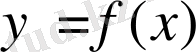 функциясының туындысы бар болса, онда
функциясының туындысы бар болса, онда
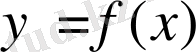 функциясы
функциясы
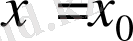 нүктесінде дифференциалданады деп аталады немесе дифферециалданатын функция деп аталады. Егер де
нүктесінде дифференциалданады деп аталады немесе дифферециалданатын функция деп аталады. Егер де
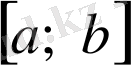 кесіндісінің әрбір ішкі нүктесінде
кесіндісінің әрбір ішкі нүктесінде
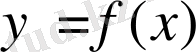 функциясының туындысы бар болса, онда
функциясының туындысы бар болса, онда
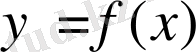 функциясы
функциясы
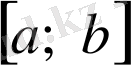 кесіндісінің ішінде дифференциалданады деп аталады немесе дифферециалданатын функция деп аталады. Функцияның дифференциалдануы, оның үзіліссіздігі сияқты, локальді қасиет екендігі түсінікті.
кесіндісінің ішінде дифференциалданады деп аталады немесе дифферециалданатын функция деп аталады. Функцияның дифференциалдануы, оның үзіліссіздігі сияқты, локальді қасиет екендігі түсінікті.
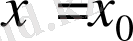 нүктесінде үзіліссіз функция ғана осы нүктеде дифференциалдануы мүмкін; бұл (1) өрнектегі бөлшектің бөлімі нольге ұмтылғанда шектің бар болуы үшін осы бөлшектің алымының да нольге ұмтылуы қажеттігінен көрініп тұр, ал бұл өз кезегінде
нүктесінде үзіліссіз функция ғана осы нүктеде дифференциалдануы мүмкін; бұл (1) өрнектегі бөлшектің бөлімі нольге ұмтылғанда шектің бар болуы үшін осы бөлшектің алымының да нольге ұмтылуы қажеттігінен көрініп тұр, ал бұл өз кезегінде
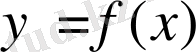 функциясының
функциясының
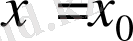 нүктесінде үзіліссіздігін білдіреді. Кері тұжырым, жалпы жағдайда, дұрыс емес; үзіліссіз функция дифференциалданбайтын болуы да мүмкін. Осындай ең қарапайым мысалдардың бірі ретінде
нүктесінде үзіліссіздігін білдіреді. Кері тұжырым, жалпы жағдайда, дұрыс емес; үзіліссіз функция дифференциалданбайтын болуы да мүмкін. Осындай ең қарапайым мысалдардың бірі ретінде
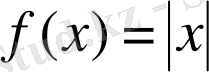 (1. 1-сурет) функциясын келтіруге болады; бұл функцияның бүкіл сан түзуінде үзіліссіз екендігін дәлелдеу қиын емес. Нақты санның модулінің (абсолют шамасының) анықтамасын қолданып
(1. 1-сурет) функциясын келтіруге болады; бұл функцияның бүкіл сан түзуінде үзіліссіз екендігін дәлелдеу қиын емес. Нақты санның модулінің (абсолют шамасының) анықтамасын қолданып
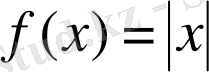 функциясын ашып жазамыз:
функциясын ашып жазамыз:

Сондықтан
 ,
,
яғни
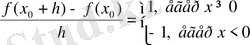 .
.
Демек
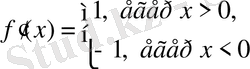 , және
, және
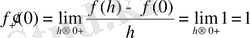 және
және
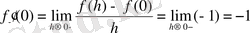 болады. Сонымен, оң жақты және сол жақты туындылар бар болып, олар
болады. Сонымен, оң жақты және сол жақты туындылар бар болып, олар
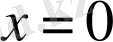 нүктесінде өзара тең емес, демек,
нүктесінде өзара тең емес, демек,
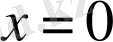 нүктесінде
нүктесінде
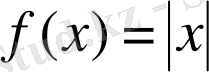 функциясының жай (екі жақты) туындысы жоқ.
функциясының жай (екі жақты) туындысы жоқ.
Егер
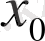 нүктесінде
нүктесінде
 функциясының оң жақты және сол жақты туындылары бар болып, бірақ жай туындысы болмаса, онда
функциясының оң жақты және сол жақты туындылары бар болып, бірақ жай туындысы болмаса, онда
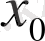 нүктесі функцияның сыну нүктесі деп аталады.
нүктесі функцияның сыну нүктесі деп аталады.
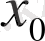 нүктесі
нүктесі
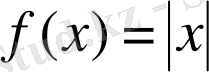 функциясының сыну нүктесі болады.
функциясының сыну нүктесі болады.
Екінші мысал ретінде графигі 1. 2-суретте келтірілген функцияны қарастыруға болады, бұл функцияның аналитикалық өрнегін келтіріп жатудың қажеті жоқ, функция үзіліссіз, бірақ
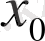 нүктесінде (1) өрнектің
нүктесінде (1) өрнектің
 және
және
 болғандағы шектері бар бола тұрып, өзара тең болмайды, бұны геометриялық тұрғыдан
болғандағы шектері бар бола тұрып, өзара тең болмайды, бұны геометриялық тұрғыдан
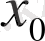 нүктесінде берілген қисықтың анықталған нақты жанамасы болмайды деп түсіндіруге болады.
нүктесінде берілген қисықтың анықталған нақты жанамасы болмайды деп түсіндіруге болады.
1. 2-сурет
0
у
х
х 0
1. 1-сурет
0
у
х
Жоғарыдағы екі мысал үзіліссіз функцияның жеке алынған нүктеде туындысы болмайтындығының мысалдары, дей тұрғанмен олардың осы туындысы жоқ нүктелерде сол жақты және оң жақты туындылары бар. Туындысы жоқ функциялар қарастырылғанда жағдай ылғи да осылай бола ма? Үзіліссіз функция бұдан да тереңірек мағынада дифференциалданбайтын жағдайлар бар екенін көрсетелік.
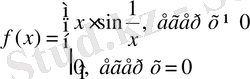 функциясын қарастырайық. Графигі 1. 3-суретте бейнеленген. Осы функцияның
функциясын қарастырайық. Графигі 1. 3-суретте бейнеленген. Осы функцияның
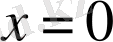 нүктесінің маңайындағы мінезін анықтайық. Кез келген
нүктесінің маңайындағы мінезін анықтайық. Кез келген
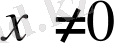 үшін
үшін
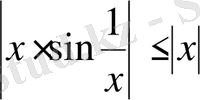 және
және
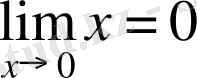 болғандықтан
болғандықтан
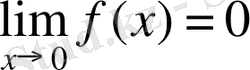 , біз, берілген функцияның
, біз, берілген функцияның
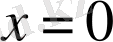 нүктесінде үзіліссіз екендігін көреміз. Бірақ
нүктесінде үзіліссіз екендігін көреміз. Бірақ
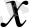 нольге ұмтылғанда, мысалы, оң жағынан ұмтылғанда
нольге ұмтылғанда, мысалы, оң жағынан ұмтылғанда
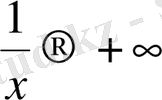 , ал
, ал
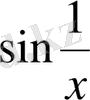 1 мен
1 мен
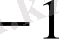 аралығында шексіз рет тербеледі;
аралығында шексіз рет тербеледі;
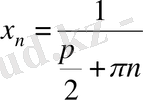 тізбегін алатын болсақ, онда
тізбегін алатын болсақ, онда
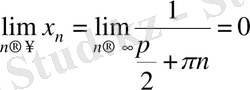 , және
, және
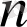 жұп (яғни
жұп (яғни
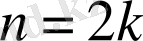 ) болғанда
) болғанда
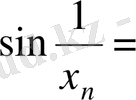
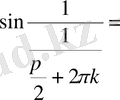
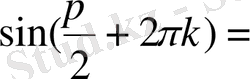
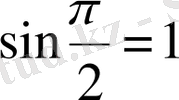 , ал
, ал
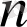 тақ
тақ
(яғни
 ) болғанда
) болғанда
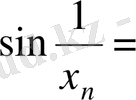
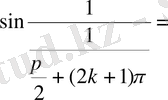
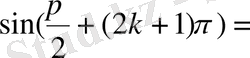
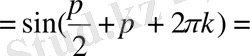
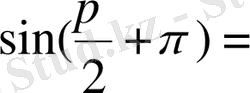
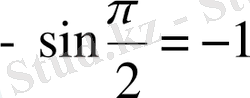 . Сондықтан
. Сондықтан
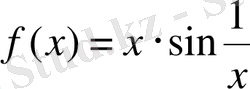
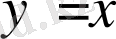 және
және
 түзулері арасында шексіз рет тербеледі де, (1) өрнек
түзулері арасында шексіз рет тербеледі де, (1) өрнек
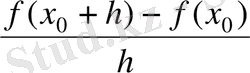
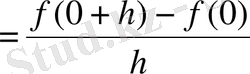
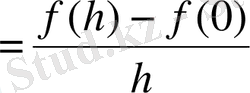
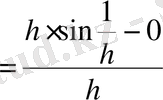
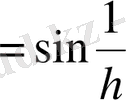 түріне келтіріліп, өзінің дербес шектері ретінде
түріне келтіріліп, өзінің дербес шектері ретінде
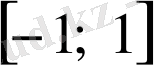 кесіндісінің кез келген мәнін
кесіндісінің кез келген мәнін
қабылдай алады; оның жоғарғы шегі
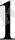 -ге тең, ал төменгі шегі
-ге тең, ал төменгі шегі
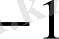 -ге тең.
-ге тең.
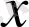 нольге сол жағынан ұмтылған жағдайда да тап осылай болады; сонымен
нольге сол жағынан ұмтылған жағдайда да тап осылай болады; сонымен
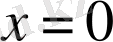 нүктесінде берілген функцияның сол жақты туындысы да, оң жақты туындысы да жоқ.
нүктесінде берілген функцияның сол жақты туындысы да, оң жақты туындысы да жоқ.
Жалпы жағдайда (1) өрнектің
 болғанда да,
болғанда да,
 болғанда да жоғарғы және төменгі шектері бар болады; бұл төрт шекті берілген функцияның берілген нүктедегі
туынды сандары
деп атайды; олардың әрқайсысы сан да бола алады,
болғанда да жоғарғы және төменгі шектері бар болады; бұл төрт шекті берілген функцияның берілген нүктедегі
туынды сандары
деп атайды; олардың әрқайсысы сан да бола алады,
 және
және
 символдарының бірі де бола алады. Сонымен, кез келген функцияның кез келген нүктеде (нүктенің қандай да бір маңайында анықталған болған жағдайында) төрт туынды саны бар болады: оң жақты жоғарғы, оң жақты төменгі, сол жақты жоғарғы, сол жақты төменгі. Егер оң жақты екі туынды сандар тең болса, онда берілген функцияның берілген нүктеде оң жақты туындысы бар болады және ол туынды туынды сандарға тең болады. Дәл осылай, егер сол жақты екі туынды сандар тең болса, онда берілген функцияның берілген нүктеде сол жақты туындысы бар болады және ол туынды туынды сандарға тең болады. Төрт
символдарының бірі де бола алады. Сонымен, кез келген функцияның кез келген нүктеде (нүктенің қандай да бір маңайында анықталған болған жағдайында) төрт туынды саны бар болады: оң жақты жоғарғы, оң жақты төменгі, сол жақты жоғарғы, сол жақты төменгі. Егер оң жақты екі туынды сандар тең болса, онда берілген функцияның берілген нүктеде оң жақты туындысы бар болады және ол туынды туынды сандарға тең болады. Дәл осылай, егер сол жақты екі туынды сандар тең болса, онда берілген функцияның берілген нүктеде сол жақты туындысы бар болады және ол туынды туынды сандарға тең болады. Төрт
1. 3-сурет
0
у
х
туынды сан да ақырлы болып, өзара тең болса (және тек осы жағдайда ғана) функция берілген нүктеде дифференциалданады. Қандай да бір нүктеде төрт туынды сандардың барлығы да шексіз болатын жағдайлар бар. Мысал ретінде
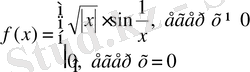 функциясын келтіруге болады. Бұл функцияның
функциясын келтіруге болады. Бұл функцияның
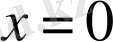 нүктесіндегі төрт туынды сандарының барлығы да шексіз екенін көрсетуге болады.
нүктесіндегі төрт туынды сандарының барлығы да шексіз екенін көрсетуге болады.
Егер жоғарыдағы суреттегі функция бейнесі әртүрлі нүктеде әрқилы екенін ескерсек, онда бір ғана функцияны дифференциалдауға қатысты қарастырғанда оның қандай күрделі құбылыс болатынын аңғаруға болады. 1. 3-ші суретте бейнеленген құбылыс тек қана оқшауланған нүктелерге ғана тән деп айтуға болмайды. Әр нүктеге қатысты құрылымы өте күрделі болатын және тұтас бір аралықта немесе бүкіл сан түзуінің бір де бір нүктесінде дифференциалданбайтын функциялар бар. Бүкіл сан түзуінде үзіліссіз, бірақ ешбір нүктеде дифференциалданбайтын функция мысалы ретінде Вандер-варден алғаш қарастырған қатар мен тригонометриялық функциялар арқылы өрнектелетін функцияны атап кетуге болады.
Туынды сандарды қолдану мысалын қарастырайық. Дифференциалданатын функциялар үшін олардың өсу мен кемуге қатысты сипаттамасы функцияның туындысының таңбасымен тығыз байланысты. Егер
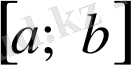 кесіндісінің барлық нүктелерінде
кесіндісінің барлық нүктелерінде
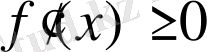 болса, онда
болса, онда
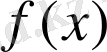 - осы кесіндіде (сегментте) кемімейтін функция, ал егер
- осы кесіндіде (сегментте) кемімейтін функция, ал егер
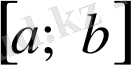 кесіндісінің барлық нүктелерінде
кесіндісінің барлық нүктелерінде
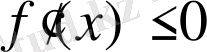 болса, онда
болса, онда
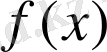 - осы кесіндіде (сегментте) өспейтін функция. Функцияның өсуі мен кемуінің бұл белгілері олардың қолдану аясы көлемінде, яғни берілген функция дифференциалданатын болған жағдайда артық ештеңені қолданбай-ақ қою мүмкіндігін қамтамасыз етеді; бірақ функция дифференциалданбайтын болған жағдайда бұлар тәріздес белгілер ештеңе бермейді; соған қарамастан онша терең емес зерттеулердің өздері функцияның өсуі мен кемуінің оларға ұқсас белгілері барлығын және ол белгілердің функцияның дифференциалданатын- тәуелсіз екендігін көрсетеді. Бұған көз жеткізу үшін келесі тұжырымды дәлелдейміз.
- осы кесіндіде (сегментте) өспейтін функция. Функцияның өсуі мен кемуінің бұл белгілері олардың қолдану аясы көлемінде, яғни берілген функция дифференциалданатын болған жағдайда артық ештеңені қолданбай-ақ қою мүмкіндігін қамтамасыз етеді; бірақ функция дифференциалданбайтын болған жағдайда бұлар тәріздес белгілер ештеңе бермейді; соған қарамастан онша терең емес зерттеулердің өздері функцияның өсуі мен кемуінің оларға ұқсас белгілері барлығын және ол белгілердің функцияның дифференциалданатын- тәуелсіз екендігін көрсетеді. Бұған көз жеткізу үшін келесі тұжырымды дәлелдейміз.
Теорема
.
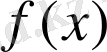 функиясы
функиясы
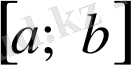 кесіндісінде үзіліссіз болсын және осы функцияның төрт туынды санының біреуі - оны
кесіндісінде үзіліссіз болсын және осы функцияның төрт туынды санының біреуі - оны
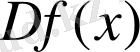 арқылы белгілейік - барлық
арқылы белгілейік - барлық
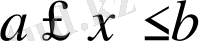 үшін теріс емес болсын, онда
үшін теріс емес болсын, онда
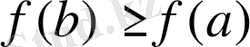 .
.
Әрине, белгінің бұл түрдегі тұжырымдалуы әдеттегі тұжырымдалуынан едәуір күштірек, себебі мұнда мәселе кез келген үзіліссіз функция (ол дифференциалданбайтын болуы да мүмкін) туралы болып тұр.
Дәлелдеу
. Теорема тұжырымына кері жорып,
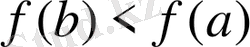 делік.
делік.
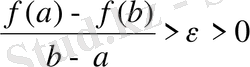 шарттарын қанағаттандыратындай
шарттарын қанағаттандыратындай
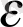 санын алайық. Анықтық үшін
санын алайық. Анықтық үшін
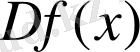 -
-
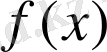 функциясының оң жақты жоғарғы туынды саны болсын.
функциясының оң жақты жоғарғы туынды саны болсын.
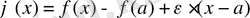 функциясын қарастырайық; сонда
функциясын қарастырайық; сонда
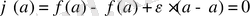 және
және
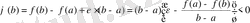 , яғни
, яғни
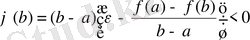 . (3)
. (3)
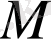 -
-
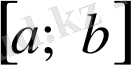 кесіндісінің
кесіндісінің
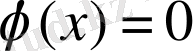 болатындай барлық нүктелерінің жиыны болсын, және
болатындай барлық нүктелерінің жиыны болсын, және
 - осы жиынның ең жоғарғы шекарасы болсын. Егер
- осы жиынның ең жоғарғы шекарасы болсын. Егер
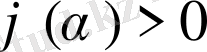 (немесе
(немесе
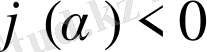 ) болса, онда
) болса, онда
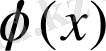 функциясы үзіліссіз болуы себепті
функциясы үзіліссіз болуы себепті
 нүктесін кез келген
нүктесін кез келген
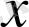 нүктесінде
нүктесінде
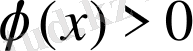 (немесе сәйкесінше
(немесе сәйкесінше
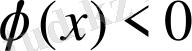 ) болатындай етіп
) болатындай етіп
 маңайымен қоршай алған болар едік. Екінші жағынан, жоғарғы шекараның анықтамасына сәйкес
маңайымен қоршай алған болар едік. Екінші жағынан, жоғарғы шекараның анықтамасына сәйкес
 нүктесінің кез келген маңайы
нүктесінің кез келген маңайы
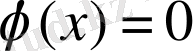 болатындай нүктелерді қамтуы керек. Бұл қарама-қайшылық
болатындай нүктелерді қамтуы керек. Бұл қарама-қайшылық
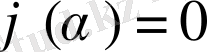 екендігін көрсетеді.
екендігін көрсетеді.
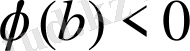 болғандықтан
болғандықтан
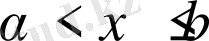 үшін
үшін
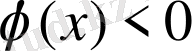 ; мұндай кез келген
; мұндай кез келген
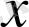 үшін
үшін
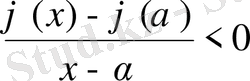 ,
,
және сол себепті
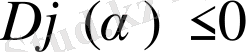 . Бірақ
. Бірақ
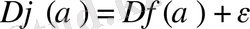 ,
,
бұдан
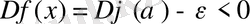 ,
,
бұл теореманың шартына қайшы келеді. Сонымен, теорема дәлелденді.
1. 2 Функцияның туындысы ұғымына алып келетін есептер
Туынды ұғымына алып келетін есептер ішінде мектеп оқушыларына таныс және олардың түсінулеріне еш қиындығы жоқ есептер бар, олардың қатарына 1. 1-параграфта келтірілген және туындының механикалық мағынасы деп аталған жылдамдық туралы есепті, сол параграфта келтірілген және туындының геометриялық мағынасы деп аталған функция графигіне белгілі бір нүктеде жүргізілген жанама туралы есепті, сонымен қатар химиялық реакцияның жылдамдығы туралы есепті және тағы басқаларын жатқызуға болады.
1. 3 Дифференциалдау ережелері
Жалпы жағдайда функцияның туындысын белгілі бір ережелерге сүйене отырып табу қажет.
Берілген
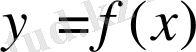 функциясының туындысын туындының анықтамасын қолдана отырып табу үшін келесі алгоритмді қолдану керек:
функциясының туындысын туындының анықтамасын қолдана отырып табу үшін келесі алгоритмді қолдану керек:
1)
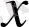 аргументіне
аргументіне
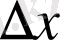 өсімшесін бере отырып функцияның өсірілген мәні табу керек:
өсімшесін бере отырып функцияның өсірілген мәні табу керек:
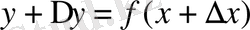 ;
;
2) функцияның сәйкес өсімшесін табу керек:
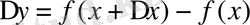 ;
;
3) функцияның өсімшесінің аргументтің өсімшесіне қатынасын құру керек:
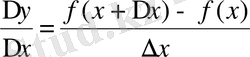 ;
;
4) қатынастың
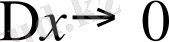 жағдайындағы шегін табу керек:
жағдайындағы шегін табу керек:
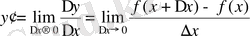 .
.
Негізгі элементар функциялардың туындыларын осы алгоритмді ұстана отырып есептеп алғаннан кейін «дифференциалдау ережелері» деп аталатын ережелерді енгізіп, содан кейін дифференциалданатын функциялардың туындыларын соңғы ережелерге сүйене отырып есептеген жөн; себебі ылғи да берілген функция туындысын жоғарыда келтірілген алгоритм арқылы тауып отыру өте қолайсыз және көп уақыт талап етеді. Жоғарыда аталған алгоритмді қолданып туындыны есептеуге мысалдар келтірейік.
1
-мысал
.
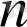 натурал сан болғанда
натурал сан болғанда
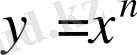 функциясының туындысы
функциясының туындысы
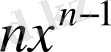 -не тең, яғни
-не тең, яғни
егер
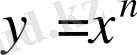 , онда
, онда
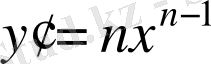 . (1)
. (1)
Дәлелдеуі . Берілген функция
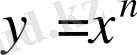 .
.
1) Егер
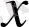 аргументіне
аргументіне
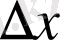 өсімшесін берсек, онда :
өсімшесін берсек, онда :
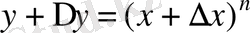 .
.
2) Ньютон биномының формуласын қолдана отырып функцияның сәйкес өсімшесін табамыз:
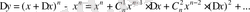
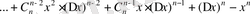
немесе
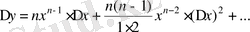
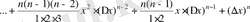 .
.
3)
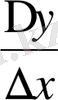 қатынасын табамыз:
қатынасын табамыз:
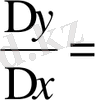
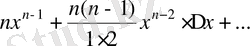
 .
.
4) Қатынастың
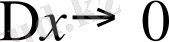 жағдайындағы шегін табамыз:
жағдайындағы шегін табамыз:
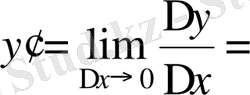
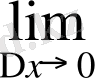
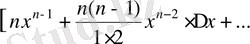
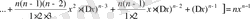 ,
,
сонымен,
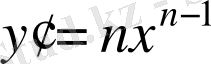 . Теорема дәлелденді.
. Теорема дәлелденді.
2
-мысал
.
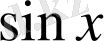 функциясының туындысы
функциясының туындысы
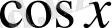 болады, яғни
болады, яғни
егер
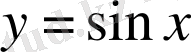 , онда
, онда
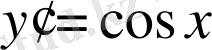 . (2)
. (2)
Дәлелдеуі . Берілген функция
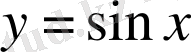 .
.
1) Егер
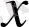 аргументіне
аргументіне
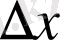 өсімшесін берсек, онда :
өсімшесін берсек, онда :
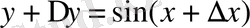 .
.
2) Ньютон биномының формуласын қолдана отырып функцияның сәйкес өсімшесін табамыз:
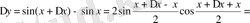
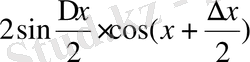 .
.
3)
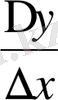 қатынасын табамыз:
қатынасын табамыз:
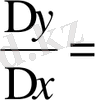
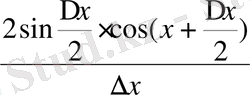
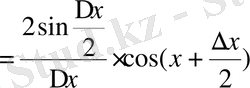
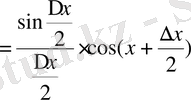 .
.
4) Қатынастың
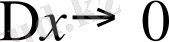 жағдайындағы шегін табамыз:
жағдайындағы шегін табамыз:
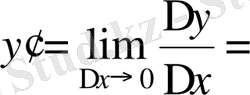
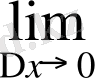
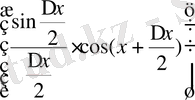

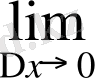
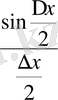
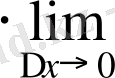
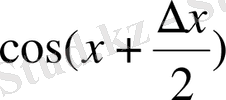

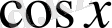 , себебі
, себебі
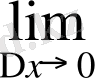
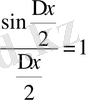 (бірінші тамаша шекті еске түсірелік) және
(бірінші тамаша шекті еске түсірелік) және
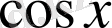 функциясы анықталу облысында үзіліссіз функция болуы себепті
функциясы анықталу облысында үзіліссіз функция болуы себепті
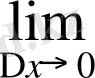
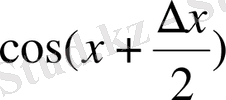
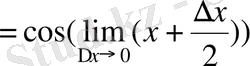
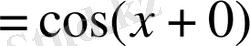
 ,
,
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz