Матроидтарда қолданылатын алгоритм

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

Мазмұны

Кіріспе . . . 2

І тарау. Матроидтарда қолданылатын алгоритм

Матроид түралы ұғым . . . 3
Циклдер матроиды, Еркін матроид, Бинарлы матроид . . . 3
Бағаналық матроид . . . 4

ІІ тарау. Негіздер мен қарапайым циклдар

2. 1 Матроидтың қарапайым циклі . . . 6

2. 2 Салдарлары . . . 7

2. 3 Матроидтар мен комбинаторлық тиімділендіру . . . 7

Қорытынды . . . 13

Пайдаланылған әдебиеттер . . . 14

Кіріспe

Алгоритмда сараң алгоритмдер маңызды рөл ойнайды, олар түсіну мен жүзеге асыру үшін қарапайым салыстырмалы жылдам жұмыс жасайды, сараң алгоритмнің көмегімен шешуге болатын көптеген әр алуан тапсырмалар белгілі. Дегенмен, көптеген тапсырмалардың нақты шешемін табу үшін сараң алгоритмді қолдану мүмкіндігін барлық уақытта дәлелдеу мүмкін емес. Бұл мақалада сараң алгоритмдердің теоретикалық негізі - матроидтер теориясы қарастыратын болады. Оның көмегі арқылы барынша жиі сараң алгоритм қолдануы мүмкіндігін орнатуға болады. Кейін анықгалғандай ол үшін көпшілік зерттеулер матроид болып табылатындығы қажет. Алдымен матроидқа анықтама беріледі, сосын матроидтармен тікелей байланысты бірқатар стандарттық тапсырмалар қарастырылатын болады.

Циклдер матройды

- Матроид бірқатар бағаналар қабырғаларының мәнінің элементтері, ал негіздер бұл бағана каркастары; матроидтар циклі ретінде бағаналардың іргетастық циклдары қызмет етеді.

Еркін матроид

- Е көбейтіндісінің өзі жалғыз ғана негіз ретінде қызмет ететін матроид.

Маршрут

- Кезектесуші жүйелілік

a=v0, e 1, v 1, e 2, …, v _n _-1 , e _n , v _n = b

Бағаналардың биіктіктері мен қабырғалары осындай е= ( v -1, v ), маршруттар биіктіктерді біріктіреді дейді. а және b маршрут соңы. Бұл жерде маршрутты тек олардың биіктіктерін есептеумен беруге болады.

а = v 0, v 1, …, v _n = b немесе оның қабырғалары е 1, е2, . . . , е _п соңғы егер

оған енетін қабырғалар саны әрине қарама-қарсы жағдайда аяқсыз.

Аяқсыз n. тек бір ғана нүктесіне ие және бір жақты аяқсыз маршрут деп аталады. Аяқсыз биіктіксіз n. екі жақты аяқсыз нүкте деп аталады.

Бинарлы мартоид

-Тұтас сандар бойынша көрсетілген матроид бағана кесіндісі матроиды мен циклді матроид және графикалық матроид бинарлы деп аталады.

Келісімділік

Әңгіме үшін алдымен осы мақалада қолданылатын терминдер себебі бойынша бағытталуы қажет. Графада цикл деп ондағы әрбір жабық жолдарды атаймыз. Онда бағана қабырғаларының әрбірі бір реттен көп кездеседі. Барлық қарастырылған бағаналар бағытталмаған. Бағаналардың бағаналық матроидтарын М деп белгілейміз. Матрицаның векторлы матроидын М (А) деп белгілейміз.

Матроид туралы ұғым

Келесі матрицаны қарастырамыз.

1001000

0101110

0010110

Е көбейтіндісін анықтаймыз. Матрица бағаналырының {1, 2, 3, 4, 5, 6, 7} нөмірлерден тұратын көбейтінді сияқты, ал 1 көбейтіндісін, Е көбейтіндісінен тұратын көбейтінді сияқты. Олармен анықталатын векторлар R заттық сандарының аймағы үстінде тәуелсіз сызықтық болып табылады. Тұрғызылған 1 көбейтіндісі қандай қасиеттерге ие деген сұрақты қоямыз.

1. Бір көбейтіндісі бос емес. Тіпті егер не бастапқы көбейтіндісі бос болса да - Е=□, егер 1 бос орынға ие көбейтіндінің бір элементінен тұрады.

і = {{□}}.

2. Бір көбейтіндісінің кез келген элементінің кез келген көбейтіндісі осы көбейтінді элементі болады. Бұл қасиет түсінікті - егер векторлардың бірқатар жиынтығы аймақ үстінде сызықтық тәуелсіз болса, онда оның кез келген жиынтығы сызықтық тәуелсіз болады.

З. Сондай-ақ бір көбейтіндісінде тағы да бір маңызды және превиальды емес қасиет бар. Егер X, Ү I, әрі [Х] =[Ү] +1, бұл кезде х Х-Ү, элементі бар. Тағы мұндай Ү□{х}□I бұл кезеңде ол біршама қызғылықты және таңғаларлық болып көрінеді. Кейіннен бұл түсінікті болады.

Матроид ұғымының өзін анықтауға өтеміз. Матроид деп - матроидтың тәуелсіз көбейтінділерінің көбейтіндісі деп аталатын 1 көбейтіндісінің және матроидтың негіздік көбейтіндісі деп аталатын Е соңғы көбейтіндісінен тұратын Е I көбейту сыңарларын айтады. Әрі 1 жоғарыда айтылған 3 қасиетті қанағаттандырады. №2 қасиет мұрагерлік қасиет деп те аталатындығын айту қажет.

Қарастырылым мысалда сызықтық тәуелсіз бағаналар көбейтіндісі шындығында да матроид болып табылатындығын дәлелдейміз. Бұл үшін матроид анықтаудын үшінші қасиетті дәлелдеу жеткілікті. Қарсы әдіс дәлелдемесін жүргіземіз.

Дәлелдеме. Х, Ү І [Х] =[Ү] +1 болсын. w Х□Ү қамтитын вектор кеңістігі болсын. Оның өлшем бірлігі [X] кем емес болуы керек. Ү□{х} барлық х Х-Ү үшін сызықтық тәуелсіз болады деп болжамдайық. Онда Ү w кеңістігінде негіз түзеді. Бұл жерде [X] dim W [Ү] . Дегенмен, X және Ү шарттары бойынша сызықтық тәуелсіз векторлардан тұрады және [Х] >[Ү], қарама-қайшылық аламыз. Векторлардың мұндай көбейтіндісі матроид болып табылады. Оны кейде векторлық матроид деп те атайды.

Бағаналық матроидты қарастырамыз

Бағаналар бағытталмаған және 4 биіктікпен тесік болып табылатын 7 қабырғадан тұрады. Айталық Е осы бағана қабырғаларынан тұратын көбейтінді болсын, Е={1, 2, 3, 4, 5, 6, 7}, ал I бағана циклі өзіне әрбір элементті иеленбейтін Е көбейтіндісінің көбейтіндісі болады. Бұл сыңар матроид болып табылады. Оны бағаналы матроид дейді және М(G) белгілейді.

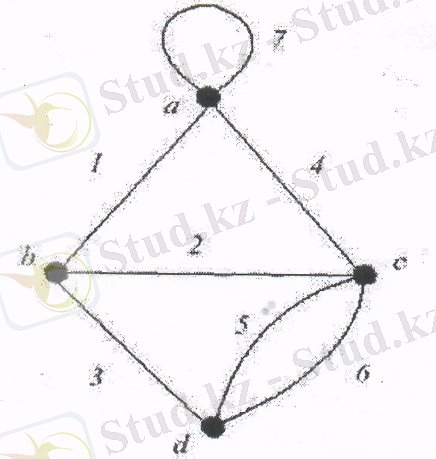
Теорема -1

Айталық 6 сызықша бағана, ал А _G - оның инциденция матрицасы. Егер де А _G -ді аймақ ішіндегі матрица ретінде қарастыратын болсақ, {0, 1}, мұнда барлық операциялар екінші модуль бойынша орындалады, осы кезде А _G - құрастырылады. Векторлық матроид өзінде циклі жоқ тәуелсіз көбейтінді ретінде көптеген қабырғаларға ие болады және М(G) =М[А _G ] .

Дәлелдеме. Х□А _G X циклға ие болған жағдайда ғана сызықтық тәуелді болатындығын дәлелдеу қажет. X өзіне С циклін иемденетіндігін болжаймыз. Егер С - тесік болса, онда X нөлдік векторға ие болады және ол сызықты тәуелсіз болады. Егерде С тесік емес болса, онда осы циклдағы әрбір биіктік С-ның екі қабырғасына сәйкес болады және екінші модуль бойынша векторлар жиынтығы нөлдік вектор болады. Осының себебінен X сызықтық тәуелді болады.

Енді X сызықтық тәуелсіз деп болжамдаймыз. D және X сызықтық тәуелді көбейтінділер аламыз. Егер де D нөлдік вектордан тұратын болса, онда X тесікке және циклға ие болады.

Егер де D нөлдік векторға ие болмаса: өйткені {0, 1} аймағында жалғыз ғана нөлдік емес элемент - 1 бар болады, онда D-дағы векторлар жиынтығы нөлдік вектор болып табылады. Бұл D - минимальды сызықтық тәуелді көбейтінді себебінен болады. Осы айтылғандардан D цикл қабырғаларына ие екендігі көрінеді және егер қандай да бір биіктікте D инцидентті қабырғасы болса, онда минимум ретінде тағы да бір оған инцидентті қабырға бар болады. Аяғында d ₁ қабырғасын аламыз және v ₀ v ₁ биіктіктері осы қабырғаларға сәйкес болсын. Айталық v ₁ биіктігіне d ₂ қандайда бір қабырғасы инцидентті болсын. Айталық v ₂ биіктігі d ₂ қабырғасының екінші ұшы болсын. Осы үрдісті жалғастырайық. Нәтижесінде екі жүйелілік алынады - v ₀ , v ₁ , . . . d ₁ , d ₂ , . . . биіктіктер саны мен D аяқты болатындықтан, мұнда v биіктіктерінің қандайда бірі қайталануы тиіс. Бұл болған кезде D-дағы цикл табылады. Сәйкес циклмен X табылады.

Негіздер мен қарапайым циклдар

Тікелей матроидтардың көмегі арқылы әр алуан міндеттерді шешуге өту үшін осы теориядан тағы да бір маңызды ұғымды қарастыру қажет. Матроидтар базасы - матроидтардың максималды тәуелсіз көбейтінділері.

Матроидтың қарапайым циклі - матроидтардың минимальды тәуелді көбейтіндісі.

Екі көбейтінді береміз - М матроидтың барлық мүмкін базаларынан тұратын көбейтінді, оны В _М деп белгілейміз және М матроидтың барлық мүмкін қарапайым циклдарынан тұратын көбейтінді, оны С _М деп белгілейміз. Матроидтар мұрагерлік қасиеттерге ие болғандықтан, бұл екі көбейтіндінің кез келгені матроидты толығымен анықтай алады.

Теорема - 2

X көбейтіндісі келесі екі қасиет орындалған жағдайда ғана М матроид базасының көбейтіндісі болып табылады:

1. В көбейтіндісі бос емес.

2. Егер де В ₁ , В ₂ □В, х□В ₁ , - В ₂ болса, онда □В ₂ -В ₁ бар болады. Бұл кезде (В ₁ -х) □{у}□В.

Дәлелдеме. Онда келтірілген екі қасиет орындалсын делік. В барлық базаға ие екендігін дәлелдеу қажет. Қайтадан қарама-қайшылықтан дәлелдеме жүргіземіз. Айталық В ₁ □В бірақ I элементі бар. Ол мұндай

В ₁ □{I}□В, І=В ₁ -В. Дегенмен бұл кезде Ү□В-(В□{I}) элементі жоқ болады.

Айталық В - базалар көбейтіндісі, екі қасиет те орын алатындығын дәлелдейміз. Алғашқы қасиет көрініп тұр. Екінші қасиетті қарастырамыз, х В ₁ -В ₂ бірақ В ₂ -В ₁ жоқ болады, мұнда В ₁ -х {y} В дегенмен бұл матроидтардың үшінші қасиетіне қарама-қайшы, өйткені [В ₁ {х}] +1=[В ₂ ] және мұндай бар болу тиіс.

Салдарлары

Кез келген базаның қуаттылығы екі қасиет бойынша бірдей болып табылады. Матроид рангасы деп оның базасының қуаттылығын атайды.

Теорема - 3

С көбейтіндісі келесі үш қасиет орындалған жағдайда ғана матроидтың қарапайым цикльдарының көбейтіндісі болып табылады:

1. С элементтерінің ешқайсысы бос көбейтінді болып табылмайды.

2. С-ның ешқандай элементі С-ның басқа элементінің көбейтіндісі болып табылмайды.

З. Егер де С ₁ және С ₂ көбейтіндісі □ С және е □ С ₁ □ С ₂ болса, онда (С ₁ □С ₂ ) - е қандайда бір С ₁ элементіне ие болады.

Дәлелдеме.

Келтірілген екі дәлелдемеге ұқсас. Оқырманға оны өз бетімен жасау ұсынылады.

Матроидтар мен комбинаторлық тиімділендіру

Матроидтар комбинаторлық тиімділенген байланысты тапсырмаларға және шешімі сараң алгоритмдерге негізделген тапсырмаларда кең қолданыс тапты.

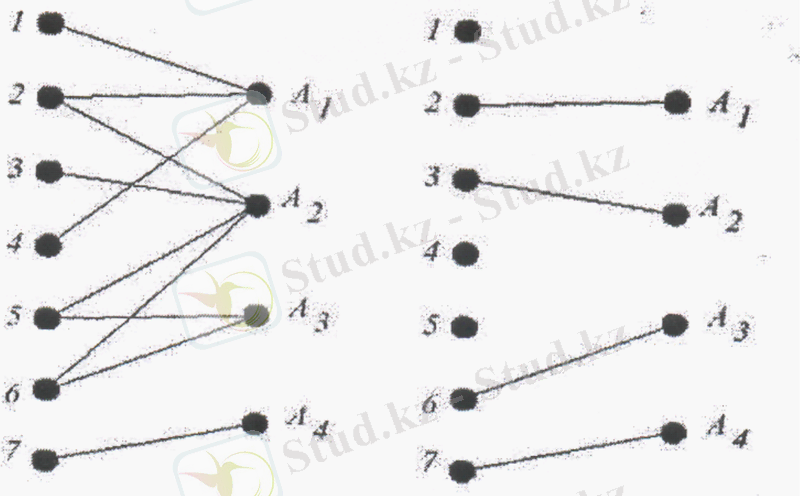
Мынадай тапсырмалар қарастырамыз: менеджерде m бір адам үшін J ₁ , J ₂ , J ₃ , J _m бір күндік жұмыс бар және ол қандайда бір жұмыс жиынтығын орындай алатын n жұмысшыларға ие. Менеджер оның жұмысшылары бір күн ішінде қандай максимальды жұмыс көлемін орындауға қабілетті екенін білгісі келеді. Кейіннен анықталғандай бұл қандайда бір матроид рангы болады.

Айталық А - қандайда бір Е көбейтіндісінің көбейтіндісі. Мысалыға, айталық А=({1, 2, 4}, {2, 3, 5, 6}, {5, 6}, {7}, көбейтінді кезінде E={1, 2, 3, 4, 5, 6, 7}. Е көбейтіндісі Е - {Х ₁ , Х ₂ , . . . , Х _k } А-жартылай трансверсалы деп аталады, егерде Ф мен {1, 2, . . . k} {1, 2, . . . , m} өзара біртектес сәйкестігі бар болса, әрі x _i □ А _Ф(i) кез келген і үшін. Егер m=k, болса, онда мұнда жартылай трансверсан трансверсаль деп аталады. Егерде {2, 3, 6, 7} көбейтіндісін алатын болсақ, онда бұл суретте сол жақтан көргеніміздей А үшін трансверсаль болады.

Теорема - 4

Айталық А Е көбейтіндісінің қандайда бір көбейтіндісі. Ал 1 - А көбейтіндісінің жартылай трансверсальдарының көбейтіндісі. Онда Е сыңары, 1 - матроид.

Дәлелдеме

Жартылай трансверсальдың әрбір көбейтіндісі - жартылай трансверсаль. Бос көбейтінді де жартылай трансверсаль. Сондықтан матроидтардың алғашқы екі қасиеті орындалады. Матроидтардың үшінші қасиетін дәлелдеу үшін екі үлесті бағана тұрғызамыз. Ол сондай-ақ максималды сыңарлар сәйкестігі мына суретте белгіленеді. Айталық сол жақтағы биіктіктер Е көбейтіндісінің элементтеріне ал оң жақтағы биіктіктер А көбейтіндісінің элементтеріне сәйкес болады. Оң жаққа сол үлестегі қабырға сол үлестің сәйкес элементі оң үлес сәйкес элементіне жататын жағдай да ғана болады. Жартылай трансверсаль болады және [X] =[Y] +1. сыңарлар сәйкестігінен Х-қа сәйкес қабырғаны көк түске, ал Y-ге сәйкесін қызыл түске бояймыз, әрі сыңарлар үйлесіміне сәйкес қабырғалар күлгін түске боялатын болады. Осылайша [X-Y] қабырғалары көк түске, [Y-X] қызыл түспен алынады және [X-Y] =[Y-X] +1 арақатынасы орындалатын болады. Бастапқы бағанадан қызыл және көк қабырғалармен индукцияланған H бағанасын қарастырамыз. Әрбір биіктік екі көк және қызыл қабырғаға не бір көк немесе қызыл қабырғаға сәйкес енеді. Байланыстылықтың кез келген бөлігі не жол, не қызыл және көк қабырғалардан кезектестірілген цикл ретінде көрінеді. Бағаналар екі үлесті болғандықтан кез келген цикл қабырғалардың жұп санынан тұрады. Өйткені көк қабырғалар қызылға қарағанда бір санға артық, мұнда көк қабырғамен басталатын және аяқталатын жол болуы тиіс. Бұл жолды H` белгілейміз. Н-ді көк және қызыл түске боялған қабырғалар бағанадағы сыңарлар үйлесімдігін түзетіндігін аламыз. Ары қарай Е көбейтіндісі осы сыңарлар үйлесіміне сәйкестеіп Y□{x} түріне ие болатындығын көрсету оңай, мұнда Х-бұл Х ал Y-ден бірқатар элемент. Бөлім басында қойылған тапсырмаға оралайық. Жартылай трансверсальдардан матроид рангасы бір күн ішінде жұмысшылар орындай алатын максимарды жұмыс көлміне тең екі үлесті бағанадағы максималды сыңарлар үйлесімі қуаттылығына сәйкес болады.

Салдар-1

В матроидтың кез келген негізі үшін М(Е) және кез келген р Е/B көбейтінді B p нақты бір циклға ие және бұл цикл p арқылы өтеді.

Келесі қадамда біз қос матроид ұғымын қарастырамыз.

Бұл қадамда біз сараң алгоритм ұғымын қарастырамыз.

Айталық Е - бос емес соңғы көбейтінді және w - R ақиқат сандары көбейтіндісіндегі Е қызметі. w (е) санын е Equation. 3 Е элементінің салмағы деп атайтын боламыз. Кез келген бос емес а Equation. 3 е мәселен

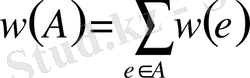
және w (А) А көбейтіндісінің салмағы деп атайтын боламыз.

Бірқатар жиынтығын ең болмағанда бір бос емес көбейтінді бар болғанда келтіреміз. В-ға салыстырмалы теориялық көбейтінділік енгізілім жартылай реттелген көбейтіндісі ретінде қарайтын боламыз. Элементтер қолайлылығы үшін жартылай реттелген көбейтінді 1 нысан деп атайтын боламыз.

Ары қарай В тәуелсіздік аксиомасын қанағаттандырады, яғни нысан көбейтіндісі нысан болып табылады деп санайтын боламыз.

Келесі тапсырманы қарастырамыз: жартылай реттелген көбейтіндіде В нысаны минимальды мүмкін салмақ максималды нысанын құрастырады.

Нысандар ұяшығына қандай жағдайларда келесі алгоритм берілген тапсырманы шешетінін зерттейміз.

Сараң алгоритм.

7. е ₁ , ретінде Е-дегі барынша аз мүмкін салмақ элементін таңдаймыз, ол мынадай {e ₁ , } B.

8. Айталық е ₁ , . . . , е _i-1 , элементтері таңдалған делік. Еі ретінде барынша аз мүмкін салмақ элементін таңдаймыз. Ол мынадай:

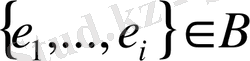Equation. 3 және Equation. 3

9. Мүмкін болғанға дейін екінші шартты орындаймыз. Үрдіс міндетті түрде аяқталады және 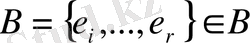максималды нысаны құрастырылады.

Айталық В - М=М(G) матроидының бірқатар негізі. Бұл кезде В сәйкес коостово деп те атайды. Лемма екі күшімен М(G) матроидының тәуелсіз көбейтінділері - сол және тек сол бағана қабырғаларының көбейтіндісі, олар әрбір негізбен бос емес қиылысуға ие. Демек, М(G) Ко тәуелді көбейтінділері - G бағанасында барлық бос топтар сүрту кезінде қирайтын сол және тек сол қабырғалар көбейтіндісі, яғни байланыстылық бөліктерінің саны ұлғаяды. Осылайша М(G) Ко тәуелді көбейтінділері - бағана қабырғаларының нақты кесуші көбейтінділері, ал онда көп циклдер - бұл кесінділер. Демек, циклдер мен бағана кесінділері - бұлар өзара қос нысандар. М*(G) матроиды М(G) матроидына қосарлы, G бағанасының кесінді матроиды деп аталады.