Инерциялық емес санақ жүйелерін дифференциалдық теңдеулер негізінде компьютерлік модельдеу: Фуко маятнигі мен Кориолис күшінің виртуалды эксперименттері


Мазмұны
Кіріспе . . . 4
І тарау. Инерциялық емес санақ жүйесі(ИЕСЖ) . . . 6
1. 1. Ілгерілемелі, айналмалы қозғалыстағы ИЕСЖ . . . 6
1. 2. Жер бетінде ИЕСЖ құбылыстарының байқалу мысалдары . . . 9
1. 3. Фуко маятнигі . . . 11
1. 4. Кориолис күші . . . 13
ІІ тарау. ИЕСЖ құбылыстарына модель құрастыруға қажетті аппараттар . . . 20
2. 1. ИЕСЖ тақырыбына модельдерді құрастыру теориясы . . . 20
2. 2. Екінші ретті дифференциалдық теңдеулерді сандық шешу жолдары . . . 20
2. 3. Компьютерлік модельдеуде қолданылған бағдарламалау тілі - Delphi. 21
ІІІ тарау. Дифференциалдық теңдеулер көмегімен жасалған модельдермен виртуальді эксперимент жүргізу . . . 23
3. 1. Фуко маятнигін сандық модельдеу . . . 23
3. 2. Жер бетіндегі Кориолис күшінің байқалуын сандық модельдеу . . . 27
Қорытынды . . . 29
Пайдаланылған әдебиеттер . . . 30
Кіріспе
Ғылыми жобаның өзектілігі:
Инерциялық санау жүйесі тұрғысынан қарағанда тыныштық қалыпта тұрмайтын немесе бірқалыпты түзу сызықты қозғалыста болмайтын санау жүйелері инерциялық емес санақ жүйелері деп аталады.
Жер бетінде болатын көптеген инерциялық емес санақ жүйелерінен пайда болатын әсерлерді біз байқамаймыз. Жердің айналуы барысында өзендер мен мұхит ағындарымен сезілетін Кариолис күші өте аз болғанымен, олардың әсерінен болатын желдер мен өзендердің орын ауыстыруы жылдар өте үлкен маңызға ие болады. Міне Жердің өз өсінен айналуы салдарынан болатын үдерістерді дифференциалдық теңдеулер арқылы модельдеу, оларды түсіну қоғамға бұрыннан керекті деп есептейміз.
Жердің географиялық ендікке байланысты ауырлық күшінің өзгеруін, мұхит ағыстарының пайда болуын дифференциалдық теңдеулерді шешу әдістерімен модельдеу олардың қозғалыс ерекшеліктерін көрнекілендіру мүмкіндігін береді. Бұл мәселені шешуде компьютерлік моделдеу мен дифференциалдық теңдеулерді шешудің сандық әдістерін қолданудың маңызы өте зор. Тарихта белгілі Фуко маятнигінің қозғалыс траекториясы функция арқылы сипатталынбайды, оның әр уақыт мезеті үшін сандық шамасын компьютерлік модель арқылы алуға болады.
«Дифференциалдық теңдеулер көмегімен физика есептерін шешу және оны компьютерлік модельдеуде пайдалану» тақырыбы қазіргі компьютерлік технологиялардың және дифференциалдық теңдеулерді сандық әдістермен шешу әдістерінің маңыздылығы осы ғылыми жобамның өзектілігін білдіреді.
Ғылыми жобаның гипотезасы:
- бағдарламалау тілінде құрылған компьютерлік модель көмегімен кез келген планетада орналасқан Фуко маятнигіне әсер ететін шамаларды (планетаның айналу периоды, географиялық ендігі, еркін түсу үдеуі) өзгерту арқылы виртуальді тәжірибелер жүргізіп, сәйкес нәтижелер алуға болады;
- компьютердегі динамикалық модельдер құбылысты толығымен түсіндіргені виртуальді тәжірибененің зертханалық жұмыстың аналогы ретінде қарастыруға болатындығын түсіндірілетіндігі болып табылады;
- Фуко маятнигіне центрден тепкіш күштің әсері тарихи тәжірибеде көрінбегенімен, идеалданған үйкеліссіз виртуальді экспериментте байқалуы тиіс және бірте-бірте амплитуда артуы керек.
Ғылыми жобаның мақсаты:
Зерттеу жұмысымның барысында физиканың күрделі тақырыптарының бірі - Механиканың инерциялық емес санақ жүйесінің физикалық заңдылықтары мен бағдарламалау тілдері арасындағы сандық байланысты қалыптастыру жолдарын ұйымдастыру, түрлі планетада орналасқан Фуко маятнигімен виртуальді тәжірибелер жүргізіу ғылыми жобамның мақсатын анықтайды.
Ғылыми жобадан күтілетін нәтиже:
Инерциялық емес санақ жүйесіне байланысты үдерістерді дифференциялдық теңдеулер көмегімен бағдарламалау тілінде модельдеу арқылы Фуко маятнигіне центрден тепкіш күштің әсерінен амплитуданың артатына көз жеткізу.
І тарау. Инерциялық емес санақ жүйесі (ИЕСЖ)
1. 1. Ілгерілемелі, айналмалы қозғалыстағы ИЕСЖ
Галилейдің салыстырмалық принципі бойынша инерциялық санау жүйесінің ішінде жүргізілген кез келген механикалық тәжірибелер жүйенің тыныштық қалыпта тұрғанын немесе оның бір қалыпты түзу сызықты қозғалыста екенін анықтауға мүмкіндік бермейді. Инерциялық санау жүйесінің ішіндегі материялық нүктелер жиынына, денеге әсер ететін қорытқы күш олардың үдеуін бір мәнді анықтауға мүмкіндік береді.
Кез келген қозғалмайды деп қаралатын жүйені инерциялық санау жүйесі ретінде алуға болады. қозғалмайтын инерциялық санау жүйесінде қарағанда бірқалыпты түзу сызықты қозғалыстағы жүйелер де инерциялық санау жүйелері болады. Инерциялық санау жүйелерінде Ньютонның екінші заңы ең қарапайым түрде жазылады:
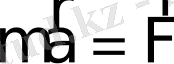
ИЕСЖ тұрғысынан Ньютонның екінші заңының түрі өзгермейтін болу үшін, формулаға кіретін үдеу абсолют қозғалысқа қатысты үдеу болу керек, яғни
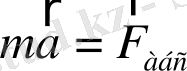 . Бірақ абсолют үдеуді анықтау салыстырмалы үдеуді анықтаудан қиынырақ екені түсінікті. Сондықтан, ИЕСЖ тұрғысынан Ньютонның екінші заңын
. Бірақ абсолют үдеуді анықтау салыстырмалы үдеуді анықтаудан қиынырақ екені түсінікті. Сондықтан, ИЕСЖ тұрғысынан Ньютонның екінші заңын
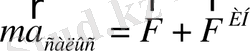 түрінде жазу ыңғайлырақ.
түрінде жазу ыңғайлырақ.
Арбаға бекітілген кронштейнге байланған жіпке жүк ілінген (1-сурет) . Арба тыныштық қалыпта тұрса немесе бірқалыпты түзу сызықты қозғалыста болса, ауырлық күші жіптің керілу күшімен Т теңгеріліп тұрады.
(1- сурет) . Арба бірқалыпты түзу сызықты қозғалады.
1. 5. 5(2) - сурет. Горизонтал жазықтықта
домалайтын түтас цилиндрдің
толық кинетикалық
энергиясын анықтау.
Енді арбаға байланған горизонтал жіпті пайдаланып, арбаға
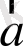 үдеу беріп, оның жылдамдығын, тасымалдау жылдамдығын арттырайық. Горизонтал жіпті тұрақты күшпен тартсақ, арба тұрақты
үдеу беріп, оның жылдамдығын, тасымалдау жылдамдығын арттырайық. Горизонтал жіпті тұрақты күшпен тартсақ, арба тұрақты
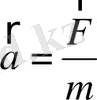 үдеу алады. Біздер жіпке ілінген дененің солға қарап ауытқып, вертикал сырықпен белгілі бір бұрыш жасағанын көреміз. Қозғалмайтын жер үстінде тұратын бақылаушы бұл құбылысты оңай түсінеді. Арбаның күш әсерінен үдеу алғаны белгілі. Бұрын белгілі бір жылдамдықпен арбаға ілесіп қозғалып келе жатқан дене инерция заңы бойынша өзінің бұрынғы жылдамдығын сақтап қалғысы келіп, арбадан бірте-бірте қала беруге мәжбүр болады. Ал арбамен бірге қозғалатын бақылаушыға бұл құбылыс түсініксіз. Көзге көрінетін еш күш жоқ болса да, жіпке ілінген жүк ауытқып тұр. Бақылаушы мынадай екі төжырымға келуі мүмкін: Ньютонның екінші заңының формуласын пайдалануға болмайды, болмаса пайдалану үшін инерция күші деп аталатын қосымша күш енгізу қажет, яғни
үдеу алады. Біздер жіпке ілінген дененің солға қарап ауытқып, вертикал сырықпен белгілі бір бұрыш жасағанын көреміз. Қозғалмайтын жер үстінде тұратын бақылаушы бұл құбылысты оңай түсінеді. Арбаның күш әсерінен үдеу алғаны белгілі. Бұрын белгілі бір жылдамдықпен арбаға ілесіп қозғалып келе жатқан дене инерция заңы бойынша өзінің бұрынғы жылдамдығын сақтап қалғысы келіп, арбадан бірте-бірте қала беруге мәжбүр болады. Ал арбамен бірге қозғалатын бақылаушыға бұл құбылыс түсініксіз. Көзге көрінетін еш күш жоқ болса да, жіпке ілінген жүк ауытқып тұр. Бақылаушы мынадай екі төжырымға келуі мүмкін: Ньютонның екінші заңының формуласын пайдалануға болмайды, болмаса пайдалану үшін инерция күші деп аталатын қосымша күш енгізу қажет, яғни
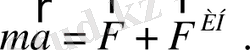
Бұл жағдайдағы инерция күшін өлшеу үшін, жүкті серіппе арқылы кронштейнмен жалғастырайық (3 - сурет) .
3-сурет. Арба үдемелі қозғалғанда жүкке әсер ететін инерциялық күшті
өлшеу.
Созылған серіппеде пайда болатын серпімділік күші
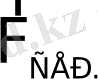 инерция күшін теңгергенше жүк арбадан қала береді, ақырында
инерция күшін теңгергенше жүк арбадан қала береді, ақырында
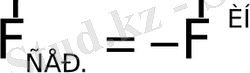 шарты орындалып, жүк арбамен бірге
шарты орындалып, жүк арбамен бірге
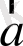 үдеумен ілгерілемелі қозғалысқа қатысады. Кинематикалық заңдылықтарды пайдаланып арбаның үдеуін, тасымалдау үдеуін табуға болады. Сонда
үдеумен ілгерілемелі қозғалысқа қатысады. Кинематикалық заңдылықтарды пайдаланып арбаның үдеуін, тасымалдау үдеуін табуға болады. Сонда
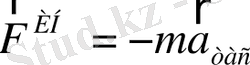
тең екені анықталады.
Ілгерілемелі ИЕСЖ тұрғысынан пайда болатын инерция күшінің шамасы дененің массасы мен оның ілгерілемелі қозғалысының үдеуінің көбейтіндісіне тең, ал бағыты тасымалдау үдеуінің бағытына қарама-қарсы болады. Бұл жағдайда Ньютонның екінші заңы былай жазылуы керек:
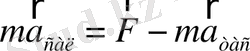
Тасымалды қозғалыстың дербес түрі бұрыштық үдеумен айналып тұрған жүйенің нүктелерінің қозғалысы. қозғалмайтын санау жүйесінің тұрғысынан қарағанда бұрыштық үдеумен айналып тұрған жүйенің әрбір нүктесі
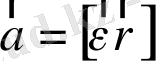
сызықтық үдеу алады, мұндағы
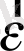 - лездік бұрыштық үдеу,
- лездік бұрыштық үдеу,
 - айналмалы қозғалыстағы жүйенің радиус - векторы, олай болса тең болады. Сондықтан, бұрыштық үдеумен айналатын санау жүйесінде әсер ететін инерция күші
- айналмалы қозғалыстағы жүйенің радиус - векторы, олай болса тең болады. Сондықтан, бұрыштық үдеумен айналатын санау жүйесінде әсер ететін инерция күші
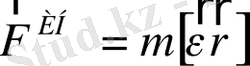
тең болуы қажет.
Тасымалды қозғалыстағы ИЕСЖ тұрғысынан Ньютонның екінші заңы
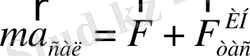 ретінде жазылу керек, ал
ретінде жазылу керек, ал
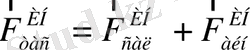
ретінде қарастырылады, яғни
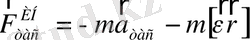 тең болады.
тең болады.
Бірқалыпты айналмалы қозғалыстағы ИЕСЖ
Тұрақты бұрыштық жылдамдықпен өз жазықтығына перпендикуляр өстен айнала алатын дискіні қарастырайық. Дискімен бірге айналатын метал шыбыққа кигізілген және дискінің центрімен серіппе арқылы жалғасқан кішкене шар берілсін. (4 - сурет) .
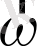

R
O


4-сурет. Диск түрақты бүрыштық жылдамдықпен перпендикуляр өстен айналады.
Диск бірқалыпты айналғанда шардың радиус бойымен жылжып дискінің центрінен қашықтағанын көреміз. Дискімен бірге айналып тұрған бақылаушы бұл құбылысты түсіндіру үшін центрден тепкіш инерция күші деп аталатын күш енгізеді де, Ньютонның екінші заңын мына түрде жазылады:
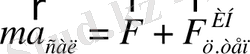
Центрден тепкіш инерция күшінің сан мәнін өлшеуге болады, себебі
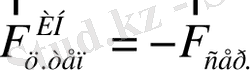
қозғалмайтын инерциялық санау жүйесінде орналасқан бақылаушы бірқалыпты айналмалы қозғалыс болу үшін центрге тартқыш үдеу болу керек екенін түсінеді және оның
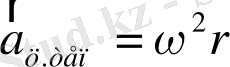 екенін де біледі, мұндағы
екенін де біледі, мұндағы
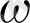 - бұрыштық жылдамдық, r - айналу өсінен қашықтық. Центрге тартқыш күш
- бұрыштық жылдамдық, r - айналу өсінен қашықтық. Центрге тартқыш күш
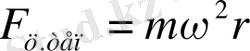 тең болады. Бұл күшті тудыратын серіппе ұзарғандағы пайда болатын
серпімділік күші
. Олай болса,
тең болады. Бұл күшті тудыратын серіппе ұзарғандағы пайда болатын
серпімділік күші
. Олай болса,
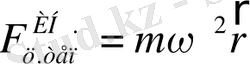
тең болады. Центрден тепкіш инерциялық күш айналу өсіне қатысты радиус - векторға қарама - қарсы бағытталады.
Центрден тепкіш инерция күші (дәл мағынасында айналу өсінен тепкіш инерция күші)
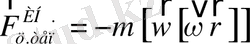
үш жағдайда нөлге тең болады:
Жер нысаны өз өсінен бірқалыпты айналғанда оның солтүстік және оңтүстік полюстерінде өске қатысты инерциялық тепкіш күштер әсер етпейді. Жер нысанының экваторы үшін өстен тепкіш инерция күші өзінің максимум мәніне ие болады:
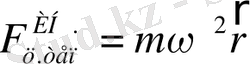
мұндағы R - Жер нысанының радиусы.
1. 2 . Жер бетінде ИЕСЖ құбылыстарының байқалу мысалдары
Жер нысаны шар деп қарастыралық. Жер бетіндегі массасы m дененің Жер нысанының центріне тартылу күші бүкіл әлемдік тартылыс заңы бойынша
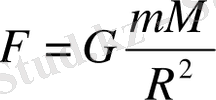
анықталады, мұндағы
 - гравитациялық тұрақты,
- гравитациялық тұрақты,
 - Жер нысанының массасы,
- Жер нысанының массасы,
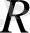 - Жер нысанының радиусы. Бұл күш Жер нысанының центріне бағытталған. Жер нысаны өз өсінен айналып тұратындықтан, жер бетіндегі кез келген денеге центрден тепкіш инерция күші әсер етеді, ол айналу өсінен есептелетін радиус - вектор бағытымен бағдарланған. Осы екі күштің геометриялық қосындысы
ауырлық күші
деп аталады (5- сурет) .
- Жер нысанының радиусы. Бұл күш Жер нысанының центріне бағытталған. Жер нысаны өз өсінен айналып тұратындықтан, жер бетіндегі кез келген денеге центрден тепкіш инерция күші әсер етеді, ол айналу өсінен есептелетін радиус - вектор бағытымен бағдарланған. Осы екі күштің геометриялық қосындысы
ауырлық күші
деп аталады (5- сурет) .
5-сурет. Жердің тәуліктік айналысының ауырлық күшіне ететін ықпалы.
Сөйтіп ауырлық күші
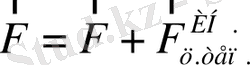 тең болады. Гравитациялық тартылу күші мен Жер экваторының арасындағы бұрыш
геоцентрлік ендік
деп аталады. Ал,
тең болады. Гравитациялық тартылу күші мен Жер экваторының арасындағы бұрыш
геоцентрлік ендік
деп аталады. Ал,
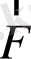 күшінің әсер ету бағытына сәйкес сызық
геометриялық вертикал
болып табылады. Ауырлық күші мен Жер экваторының арасындағы бұрыш ϒ астрономиялық ендік деп аталады да сәйкес вертикал
шын вертикал
деп есептелінеді. Егерде
күшінің әсер ету бағытына сәйкес сызық
геометриялық вертикал
болып табылады. Ауырлық күші мен Жер экваторының арасындағы бұрыш ϒ астрономиялық ендік деп аталады да сәйкес вертикал
шын вертикал
деп есептелінеді. Егерде
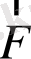 және
және
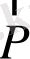 күштерінің арасындағы бұрыш
күштерінің арасындағы бұрыш
 -ге тең болса, онда
-ге тең болса, онда
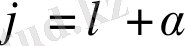 тең болады.
тең болады.
Центрден тепкіш инерция күшін гравитациялық күш бағытына, яғни геоцентрлік вертикал бағытына проекциялайық. Ол
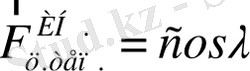 - ге тең болады. Айналу радиусы
- ге тең болады. Айналу радиусы
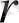 және Жер нысаны радиусы
және Жер нысаны радиусы
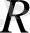 арасында
арасында
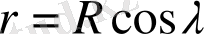
тәуелділігі бар екені түсінікті. Сондықтан
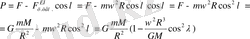
Жер бетіндегі кез келген дененің ауырлық күші геометриялық ендіктен тәуелді болады, яғни
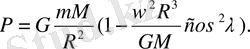
Жердің полюсінде
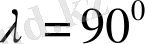 , яғни
, яғни
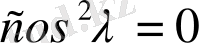 , олай болса
, олай болса
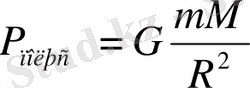
тең болады. Сонда ауырлық күші үшін мынандай тәуелділікті шығарып алуға болады:
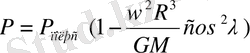
Ауырлық күшінің әсерінен Жердің бетінде кез келген дене
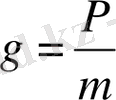 тең үдеу алады. Бұл үдеу ауырлық күшінің үдеуі деп аталатыны белгілі (еркін түсу үдеуі деп те аталады) . Сөйтіп, ауырлық күшінің үдеуі үшін мынандай формула алынады:
тең үдеу алады. Бұл үдеу ауырлық күшінің үдеуі деп аталатыны белгілі (еркін түсу үдеуі деп те аталады) . Сөйтіп, ауырлық күшінің үдеуі үшін мынандай формула алынады:
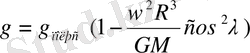
Осы формуладағы
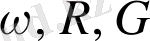 және
және
 мәндерін қойып, соңында мынандай формула шығарып аламыз:
мәндерін қойып, соңында мынандай формула шығарып аламыз:
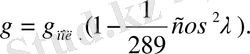
Жердің экваторындағы ауырлық күшінің үдеуі (
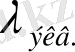 )
)
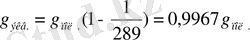
тең болады.
Геоцентрлік және астрономиялық ендіктердің айырмасы түрлі бойлықтар үшін әртүрлі болады, ең үлкен айырма
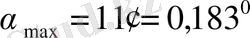 тең болады. Сондықтан көпшілік оқулықтарда жоғарыдағы формула мына түрде беріледі:
тең болады. Сондықтан көпшілік оқулықтарда жоғарыдағы формула мына түрде беріледі:
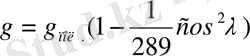
1. 3. Фуко маятнигі
 ФУКО, ЖАН БЕРНАР ЛЕОН (Foucault, Jean-Bernard-Léon) (1819-1868) - Француз физигі 1819жылы 18 қыркүйекте дүниеге келді. Әкесінің қалауымен дәрігерлік ілімін оқығанмен, эксперементтік физикамен әуестенген болатын. 1845жылы “Пікірталас журналы” газетінің ғылыми шолушысы, 1855жылы Париждік обсерваториясының қызметкері, 1862жылы Бюро долготтың мүшесі болды. Негізгі зерттеулері оптика, механика, электромагнетизмге қатысты болды. А. Физамен бірге бірнеше оптикалық зерттеулер жасаған, солардың ішіндегі әйгілісі - жарық интерференциясын бақылау. 1849-1850жылдары жылдам айналатын айнаны пайдаланып, ауа мен судағы жарық жылдамдығын өлшеді. 1851жылы Жердің өз осін айналатынын дәлелдейтін, маятникпен тәжірибе істеді. Фуко - Лондон королінің қоғамының мүшесі, Берлиндік ғылым академигі, Копли медалімен марапатталған болатын. 1868жылы 11 акқпанда Француз физигі көз жұмды.
ФУКО, ЖАН БЕРНАР ЛЕОН (Foucault, Jean-Bernard-Léon) (1819-1868) - Француз физигі 1819жылы 18 қыркүйекте дүниеге келді. Әкесінің қалауымен дәрігерлік ілімін оқығанмен, эксперементтік физикамен әуестенген болатын. 1845жылы “Пікірталас журналы” газетінің ғылыми шолушысы, 1855жылы Париждік обсерваториясының қызметкері, 1862жылы Бюро долготтың мүшесі болды. Негізгі зерттеулері оптика, механика, электромагнетизмге қатысты болды. А. Физамен бірге бірнеше оптикалық зерттеулер жасаған, солардың ішіндегі әйгілісі - жарық интерференциясын бақылау. 1849-1850жылдары жылдам айналатын айнаны пайдаланып, ауа мен судағы жарық жылдамдығын өлшеді. 1851жылы Жердің өз осін айналатынын дәлелдейтін, маятникпен тәжірибе істеді. Фуко - Лондон королінің қоғамының мүшесі, Берлиндік ғылым академигі, Копли медалімен марапатталған болатын. 1868жылы 11 акқпанда Француз физигі көз жұмды.
 Фуконың көпшілік алдындағы ең алғашқы көрсетілімі 1851 жылы Париждік Пантеонда өтті. Пантеон күмбезінің астына ұзындығы 67 метр болатын ұшты құрыш сымға бекітілген массасы 28 килограммдық шарды іліп қойды. Бекітпе нүктесінде диаметрі - 6 метр болатын дөңгелек қоршау жасалды, маятник өзінің қозғалыстағы қиылысу кезіндегі өрнегін сызу үшін, қоршаудың шетіне құм төселді. Әрбір тербеліс кезінде алдыңғы қиылысуынан ауытқуы-3мм-ді құрады. Бір сағат ішінде маятник тербелісінің жалпақтығы сағат тілінің 11
0
-на бұрылған болатын, яғни шамамен 32 сағат ішінде толық айналым жасайтын. Жердің солтүстік және оңтүстік полюсінде Фуко маятнигінің тербеліс жалпақтығы 360
0
-қа бұрылыс жасайды.
Фуконың көпшілік алдындағы ең алғашқы көрсетілімі 1851 жылы Париждік Пантеонда өтті. Пантеон күмбезінің астына ұзындығы 67 метр болатын ұшты құрыш сымға бекітілген массасы 28 килограммдық шарды іліп қойды. Бекітпе нүктесінде диаметрі - 6 метр болатын дөңгелек қоршау жасалды, маятник өзінің қозғалыстағы қиылысу кезіндегі өрнегін сызу үшін, қоршаудың шетіне құм төселді. Әрбір тербеліс кезінде алдыңғы қиылысуынан ауытқуы-3мм-ді құрады. Бір сағат ішінде маятник тербелісінің жалпақтығы сағат тілінің 11
0
-на бұрылған болатын, яғни шамамен 32 сағат ішінде толық айналым жасайтын. Жердің солтүстік және оңтүстік полюсінде Фуко маятнигінің тербеліс жалпақтығы 360
0
-қа бұрылыс жасайды.

Фуко маятнигі Жердің айналатынын дәлелдеді. Ол биіктігі 7, 5метр болатын әйнектелген пирамиданың ішінде құрыш сымнан ілінген шарды құрайды.
Минсктің жазықтығында жұлдыздық тәулік ішінде маятник 290 0 -қ доға сызады, яғни сағатына 12 0 -жылжиды.
Минскідегі Педуниверситетіндегі Фуко маятнигі - Белорусиядағы 1-ші және ТМД-дағы 3-ші болып табылады. Бүкіл әлемде осындай аспап 20 шақты, соның ішінде АҚШ-та, Францияда, Румынияда, Австралияда, Кувейтте.
 1. 4. Кориолис күші
1. 4. Кориолис күші
Айналып тұрған ИЕСЖ тұрғысынан салыстырмалы қозғалыстағы денені қарастыралық. Салыстырмалы қозғалысты зерттеу оңай болу үшін әртүрлі дербес жағдайларды тексерейік. Диск өзінің симметрия центрінен өтетін және оның жазықтығына перпендикуляр болатын өстен бірқалыпты айналып тұрсын. Айналу бағыты сағат тілінің қозғалу бағытына қарама-қарсы деп қарайық (6- сурет ) .
6 - сурет. Дененің айналып түрған дискінің бойымен қозғалуы.
Материялық нүкте А орнынан бірқалыпты қозғалып
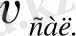 жылдамдықпен радиус - вектор бойымен жылжысын. Егер диск айналмайтын болса, материялық нүкте
жылдамдықпен радиус - вектор бойымен жылжысын. Егер диск айналмайтын болса, материялық нүкте
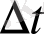 уақыт аралығында AB=
уақыт аралығында AB=
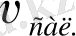
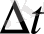 жол жүрер еді. Осы уақыт аралығында диск
жол жүрер еді. Осы уақыт аралығында диск
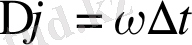 бұрышқа бұрылады. Олай болса, екі қозғалысқа қатысатын материялық нүкте
бұрышқа бұрылады. Олай болса, екі қозғалысқа қатысатын материялық нүкте
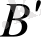 орынға келеді. Сырттан қараған бақылаушыға материялық нүкте Д орнына келетін сияқты болып көрінеді, басқаша айтқанда салыстырмалы қозғалыстағы материялық нүктеге әсер ететін, сондықтан оған қосымша
орынға келеді. Сырттан қараған бақылаушыға материялық нүкте Д орнына келетін сияқты болып көрінеді, басқаша айтқанда салыстырмалы қозғалыстағы материялық нүктеге әсер ететін, сондықтан оған қосымша
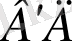 жол жүруге мүмкіндік бермейтін инерция күші болуы қажет. Бұл инерция күшін ең бірінші рет салыстырмалы қозғалыс теориясына енгізген француз механигі Гюстав Кориолис (1795 - 1843) . Сондықтан ол Кориолис күші деп аталады.
жол жүруге мүмкіндік бермейтін инерция күші болуы қажет. Бұл инерция күшін ең бірінші рет салыстырмалы қозғалыс теориясына енгізген француз механигі Гюстав Кориолис (1795 - 1843) . Сондықтан ол Кориолис күші деп аталады.
Кориолис күшінің сан мәнін табайық. Ол үшін
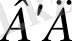 жолы мен
жолы мен
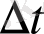 уақыт аралығындағы тәуелділікті анықтайық. Егер
уақыт аралығындағы тәуелділікті анықтайық. Егер
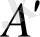 нүктесіне қатысты центрлік бұрыш
нүктесіне қатысты центрлік бұрыш
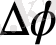 тең болса, онда
тең болса, онда
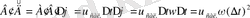
яғни
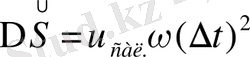
Жүру жолы жүру уақытының квадратына пропорционал, бұл бірқалыпты үдемелі қозғалыстың қасиеті. Бірқалыпты үдемелі қозғалыстың жолын анықтайтын формуланы пайдаланайық:
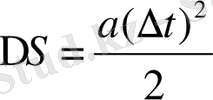 сондықтан жоғарыдағы жағдайды қамтамасыз ету үшін материялық нүктеге әсер ететін үдеу
сондықтан жоғарыдағы жағдайды қамтамасыз ету үшін материялық нүктеге әсер ететін үдеу
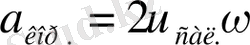
болуы қажет. Сонымен Кориолис күші
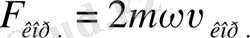
тең болады. Сонда 7- суреттен Кориолис күшінің бағыты Кориолис үдеуінің бағытына қарама-қарсы екені көрініп тұр.
Қозғалмайтын санау жүйесінің тұрғысынан қарағанда Кориолис күшінің табиғатын былай түсіндіруге болады. Айналып тұрған дискінің әр нүктесінің сызықтық жылдамдығы
 айналу өсінен есептелетін қашықтықтан тәуелді. Дискінің центрінен қашықтаған сайын сызықтық жылдамдық арта береді. Радиус бойымен бірқалыпты жылдамдықпен қозғалу үшін материялық нүктенің жылдамдығы белгілі мезетте келген нүктесінің сызықтық жылдамдығынан артық болмауы керек, сондықтан радиус бойымен қозғалатын материялық нүктеге әсер ететін күш пайда болады.
айналу өсінен есептелетін қашықтықтан тәуелді. Дискінің центрінен қашықтаған сайын сызықтық жылдамдық арта береді. Радиус бойымен бірқалыпты жылдамдықпен қозғалу үшін материялық нүктенің жылдамдығы белгілі мезетте келген нүктесінің сызықтық жылдамдығынан артық болмауы керек, сондықтан радиус бойымен қозғалатын материялық нүктеге әсер ететін күш пайда болады.
Ол күштің бағыты қозғалу бағытымен салыстырғанда оң жаққа бағдарланған (7 - сурет) .
Екінші дербес жағдайды қарастыралық. Айналып тұрған дискінің үстінде материялық нүкте айналу радиусы тұрақты шеңбер бойымен
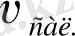 жылдамдықпен орын ауыстырсын (8- сурет) .
жылдамдықпен орын ауыстырсын (8- сурет) .
Материялық нүкте бір бағдарланған екі қозғалысқа қатысады:
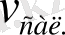 жылдамдықпен диск бетінде қозғалады және дискімен бірге бірқалыпты айналады. Сондықтан ол нүктенің
абсолют
жылдамдығы
жылдамдықпен диск бетінде қозғалады және дискімен бірге бірқалыпты айналады. Сондықтан ол нүктенің
абсолют
жылдамдығы
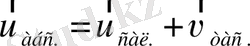
ал сан мәні
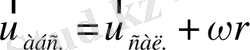 тең болады. Сонда центрден тепкіш инерция күші
тең болады. Сонда центрден тепкіш инерция күші
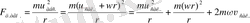
Бірінші центрден тепкіш инерция күші салыстырмалы жылдамдық салдарынан пайда болған инерция күші, екінші инерция күші дискінің бірқалыпты айналу салдарынан пайда болған инерция күші, ал үшінші қосынды өзімізге таныс Кориолис күші. Бұл күштің бағыты қозғалыс бағытымен қарағанда оңға бағытталатыны түсінікті, себебі ол центрден тепкіш күш ретінде көрініп тұр.
Егер
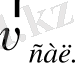 радиус бойымен бағдарланбай, онымен белгілі бір
радиус бойымен бағдарланбай, онымен белгілі бір
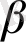 бұрышын жасайтын болса, бірақ дискінің жазықтығында жатса, оны екі құраушыға жіктеуге болады (9 - сурет: радиус - векторға параллель құраушы
бұрышын жасайтын болса, бірақ дискінің жазықтығында жатса, оны екі құраушыға жіктеуге болады (9 - сурет: радиус - векторға параллель құраушы
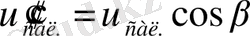
және оған перпендикуляр құраушы
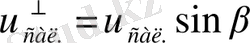
Сондықтан, алдыңғы дәлелдер бойынша
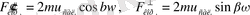
тең болады, олай болса толық (қорытқы) Кориолис күші -
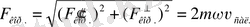
Ақырында,
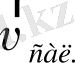 векторы мен
векторы мен
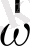 бұрыштық жылдамдық векторының арасындағы бұрыш
бұрыштық жылдамдық векторының арасындағы бұрыш
 болатын жағдайды қарастыралық (10 - сурет) . Сонда
болатын жағдайды қарастыралық (10 - сурет) . Сонда
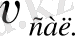 екі құраушыға жіктеуге болады: айналыс өсіне параллел құраушы
екі құраушыға жіктеуге болады: айналыс өсіне параллел құраушы
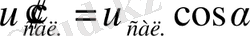 және оған перпендикуляр құраушы -
және оған перпендикуляр құраушы -
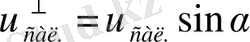 . Тек қана екінші құраушының әсерінен материялық нүкте диск бетінде өзінің орнын өзгертуі мүмкін. Олай болса
Кориолис күшінің
пайда болуына себепші тек қана екінші құраушы, сондықтан оны мына тұрғыда жазамыз:
. Тек қана екінші құраушының әсерінен материялық нүкте диск бетінде өзінің орнын өзгертуі мүмкін. Олай болса
Кориолис күшінің
пайда болуына себепші тек қана екінші құраушы, сондықтан оны мына тұрғыда жазамыз:
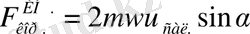
Векторлық алгебрадан белгілі екі вектордың векторлық көбейтіндісінің модулі
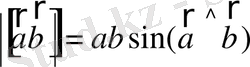 туралы теореманы пайдаланып Кориолис күшін векторлық түрде былай жазамыз:
туралы теореманы пайдаланып Кориолис күшін векторлық түрде былай жазамыз:
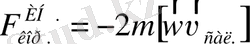
сонда
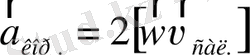 Олай болса, Кориолис үдеуінің векторы екі еселенген бұрыштық жылдамдық векторы
Олай болса, Кориолис үдеуінің векторы екі еселенген бұрыштық жылдамдық векторы
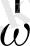 мен салыстырмалы жылдамдық векторы
мен салыстырмалы жылдамдық векторы
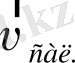 векторлық көбейтіндісіне тең.
векторлық көбейтіндісіне тең.
Сонымен, Кориолис күші үш жағдайда нөлге тең болуы мүмкін:
- егер дене өзінің симметриялық өсінен айналмаса, яғни;
- айналып тұрған дененің бетінде салыстырмалы қозғалыс болмаса, яғни;
- салыстырмалы қозғалыс жылдамдығы бұрыштық жылдамдық векторының бағытымен сәйкес келсе, яғнинемесе оған қарама-қарсы бағытта болса, яғни;
қалған жағдайларда айналып тұрған ИЕСЖ тұрғысынан қарағанда әр уақытта Кориолис күші өзін байқатады.
Жер бетіндегі Кориолис күшінің байқалуы
Жер нысаны массалар центрінен өтетін өстен бірқалыпты
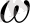 бұрыштық жылдамдықпен солтүстік полюс жақтан қарағанда сағат тілінің бағытына қарама-қарсы батыстан шығысқа қарай айналады делік. Жер бетінде меридиан бойынша салынған рельстер арқылы салыстырмалы жылдамдығы
бұрыштық жылдамдықпен солтүстік полюс жақтан қарағанда сағат тілінің бағытына қарама-қарсы батыстан шығысқа қарай айналады делік. Жер бетінде меридиан бойынша салынған рельстер арқылы салыстырмалы жылдамдығы
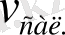 болатын пойыз жүріп келе жатсын. Пойызға әсер ететін Кориолис күші солтүстік жарты шарда пойыздың салыстырмалы қозғалу бағытына келтірілгенде оңға қарай бағытталатыны белгілі. Сондықтан, пойыз солтүстіктен оңтүстік жаққа қарай жүретін болса, онда Кориолис күші оң рельске бағдарланады да оң рельс сол жақ рельстен көбірек тозады, мүжіледі, көбірек жөндеуді талап етеді. Екі рельстің тозу, мүжілу шамасы бірдей болу үшін пойыз екі қарама-қарсы бағытта бірдей жиілікпен жүруі қажет, мысалы, Алматы - Мәскеу және Мәскеу - Алматы пойыздары. Пойыздар параллел бағытымен жүретін болса, Кориолис күші солтүстік жарты шарда оңтүстік рельске түседі, сондықтан параллел бағытта жүретін пойыздарда қосарлануы керек, мысалы, Астана-Киев және Киев - Астана.
болатын пойыз жүріп келе жатсын. Пойызға әсер ететін Кориолис күші солтүстік жарты шарда пойыздың салыстырмалы қозғалу бағытына келтірілгенде оңға қарай бағытталатыны белгілі. Сондықтан, пойыз солтүстіктен оңтүстік жаққа қарай жүретін болса, онда Кориолис күші оң рельске бағдарланады да оң рельс сол жақ рельстен көбірек тозады, мүжіледі, көбірек жөндеуді талап етеді. Екі рельстің тозу, мүжілу шамасы бірдей болу үшін пойыз екі қарама-қарсы бағытта бірдей жиілікпен жүруі қажет, мысалы, Алматы - Мәскеу және Мәскеу - Алматы пойыздары. Пойыздар параллел бағытымен жүретін болса, Кориолис күші солтүстік жарты шарда оңтүстік рельске түседі, сондықтан параллел бағытта жүретін пойыздарда қосарлануы керек, мысалы, Астана-Киев және Киев - Астана.
º
А
В
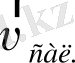
11 - сурет. Кориолис күшін зеңбірек
снарядтарының қозғалысын
зерттегенде ескеру.
Кориолис күшін зеңбірек снарядтарының, зымырауықтардың қозғалысын зерттегенде де ескеру қажет. Мысалы, зеңбірек снаряды меридиан бойымен қозғалып, солтүстік бағыттағы нысанаға атылсын. Сонда Кориолис күшінің әсерінен ол бірте-бірте шығыс жаққа қарай ығысады. Нысана неғұрлым алыс болған сайын ығысудың шамасы да артып, снаряд нысанаға тимейді. Артиллеристер зеңбіректі атар алдында келешек ығысуды есептеп, снарядтың ұшып шығу бағытын реттеулері керек (11 - сурет) .
Солтүстік жарты шарда меридиан бағытымен ағатын өзен суының әрбір тамшысына әсер ететін Кориолис күші жоғарыда айтылғандай оң жаққа қарай бағытталады. Сол себептен мұндай өзендердің ағу бағытымен есептегенде оң жағалары көбірек мүжіліп, биік жарлар пайда болады. Мысалы, Жайық өзені меридиан бойымен Орал тауларынан басталып, Каспий теңізіне құяды. Кориолис күшінің салдарынан Жайық өзенінің батыс жағасы көбірек мүжіледі. Батыс жағалауда орналасқан үйлердің, ғимараттардың өзен суына құлап кету қаупы көбірек. Сондықтан, қалаларды тұрғызғанда белгілі бір жағалар алдынала бекітілуі керек: тас, гранит немесе мрамор жағалаулар.
Қарақалпақ Республикасының бұрынғы астанасы Тұрткөлдің тағдыры мұны дәлелдейді. Тұрткөл Амудария өзенінің ағыс бағытымен есептегенде оң жағасына салынған екен. Ағысы күшті өзен ақырында Тұрткөл қаласын жойып жібереді, жаңа астана Нүкіс қаласын тұрғызуға мәжбүр етті.
Кориолис күшін тек қана артиллеристер мен архитекторлар емес, сонымен бірге метеорологтар, синоптиктер де ескеруі қажет. Циклондар және антициклондар қалай пайда болады деген сұрақтарға жауап іздейік. Күн сәулелерінің әсерінен солтүстік жарты шардағы бір аймақ қатты қызған болсын. қызған ауа вертикал жоғары көтеріліп, ол аймақта ауаның қысымы төмендейді. қалыпты қысымды көршілес аймақтардан жер бетімен ығысып ауа келе бастайды, жел соғады. Кориолис күшінің салдарынан соққан желдің әрбір молекуласы оңға қарап ығысады. қозған аймаққа жақындаған сайын мұндай ығысу күштірек болады (12 - сурет) .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz