Өндірістік модельдеуде сызықтық бағдарламалау есептерінің графиктік түсіндірмесі


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:
1. Кіріспе.
Соңғы жылдары халық шаруашылығын тиімді басқаруда матиматикалық әдістер мен есептеуіш техникалар жиі қолданылуда, Есептеуіш техникаларды дұрыс пайдалану үшін, экономиканың әртүрлі саласында болатын заңдар мен құбылыстардың ағымын біліп қана қою жеткіліксіз. Ол үшін шаруашылықты басқаруға қажетті барлық ақпараттар мен мәліметтерді белгілі бір математикалық өрнектер түрінде бейнелеу қажет.
Зерттегелі отырған экономикалық процесті немесе құбылысты белгілі бір математикалық өрнектер түрінде бейнелеу дегеніміз - сол процестің немесе құбылыстың математикалық моделін құру деген сөз. Модель құру үшін экономикалық құбылыстар мен процестер белгілі бір дәрежеде абстракцияланады. Математикалық моделін құру барысында шаруашылықта болатын құбылыстар мен процестердің ең басты қасиеттері іріктелініп, математикалық өрнектер түрінде бейнеленеді.
2. Негізгі бөлім
2. 1. Проблемалық есептің қойылымы
Айталық, өндіріс орны үш топ станокты пайдаланып, екі түрлі зат
шығаратын болса және тәулігіне 1-топтағы станоктар 400 сағат, II-топтағы станоктар 360 сағат, ал III-топтағы станоктар 3200 сағат жұмыс атқара алсын. Сонымен қатар бір дана әрбір затты шығаруға жұмсайтын станоктардың уақыты төмендегі 2. 2-кестеде көрсетілгендей болсын.
2. 2 -кесте
Станоктар
топтары
2. 2. Есептің математикалық моделін құру
2. 2. 1. Әдісті таңдау негізі
- Белгілеулер енгіземіз:
1-ші затты - А заты, 2-ші затты - B заты деп белгілейміз.
- Станоктар бойынша шектеулер:
І топтағы станок үшін:
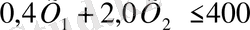
ІІ топтағы станок үшін:
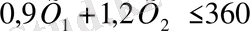
ІІІ топтағы станок үшін :
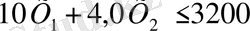
- Пайданың ең үлкен мәнің табу керек.
Теріс болмау шарты: х 1 ≥ 0,
х 2 ≥ 0.
2. 2. 2. Есеп модельдерінің сандық берілуі
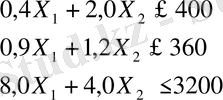 (1)
(1)
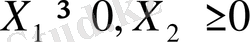 (2)
(2)
Мақсат функциясы:
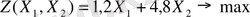 (3)
(3)
Табу керек: x=(x 1 , x 2 )
А және В заттарын белгілі мөлшерде жасау және max пайда түсіретін жоспарды табу.
2. 3. Әдісті таңдау негізі
Жалпы математикалық программалау пәні өмірдің қажеттілігінен пайда болған қолданбалы математиканың ең негізгі бөлімі. Жоғарыда айтылғандай математикалық программалаудың ішіндегі барлық халық шаруашылығына көп таралғаны, әртүрлі әдістері терең зерттелген бөлімі сызықты программалау әдістері болып есептелінеді. Математикалық программалау пәнінің ең негізгі бөлімі сызықты программалау есептері дүние жүзінде бірінші рет 1930 жылдары жарық көрді. Сызықты программалау есептері басқа тәжірибелік есептерге қарағанда өте қарапайым, зерттеуге ыңғайлы.
Сызықты программалаудың дербес есебінің бірі - қатынас есебінің дербес түрі 1931жылы Венгрияда басылып шықты, бұл мақаланың авторы математик Эгервари болатын. Кейінірек келе бұл мақаланың негізінде бірнеше еңбектер жазылды. Бұған мысал үшін 1951 және 1956 жылдары жарыққа шыққан Кун Х. В. және Таккер А. В., 1957ж. жазылған Форд Х. Р. және Фалкерсон Д. Р. еңбектерін алуға болады. Бұл еңбектерде қатынас есептерін шешуге арналған әдістер көрсетілген, кейін келе әдебиеттерде бұл әдісті қатынас есептерін шешудегі Венгер әдісі дейтін болды. Сызықты программалау атты термин алғаш рет 1940 жылдары АҚШ-та қолданылды. Сызықты программалау әдісінің арнайы есептерінің бірі 1941 жылы АҚШ-та басылып шықты, оның авторы Хичкок Ф. Л. болатын.
Бұрынғы Кеңестер Одағында сызықты программалау әдісінің негізін қалаушы академик Л. В. Канторович болды. Себебі оның көптеген сызықты программалау әдістеріне арналған дербес есептері 1930 жылдардан бастап жарыққа шыға бастады. 1956 жылы Дж. Данциг, Х. Р. Форд және Д. Р. Фалкерсон Венгер әдісінің негізінде сызықты программалаудың есептерін шешуге арналған. Л. В. Канторович ұсынған потенциал әдісіне өте сәйкес әдіс ұсынды. Ал 1947жылы Дж. Б. Дациг сызықты программалау әдістерінің ішіндегі әмебап симплекс әдісін жарыққа шығарды. Бірақ бұл әдістің Л. В. Канторовичтың 1939 ж. ұсынған, біртіндеп жақсарту әдісінен айырмашылығы өте аз болатын. Өкінішке орай бұл әдісті Л. В. Канторович бұрын ұсынса да көптеген әдебиеттерде, оқулықтарда симплекс әдісін Дж. Дациг әдісі деп атайды.
Графиктік әдіс сызықты программалау есептері тек екі белгісізден ғана құрылғанда қолданылады, ал қиынға соғады. Теория жүзінде екі және үш белгісізі бар есептерді графиктік жолмен шешкен сияқты кез келген белгісізі бар есептер де графиктік жолмен шешіледі деп қарастыруға болады. Өйткені егер белгісіздің саны екеу болса, есептің анықталу аймағы жазықтықта жатқан дөңес көпбұрышты береді. Егер белгісіздің саны үшеу болса, онда есептің анықталу аймағы кеңістікте жатқан үш өлшемді дөңес көп жақтыны береді. Егер шектеуші шарттар мынадай белгісізден тұрса:
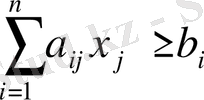 (i=1, 2, …, m)
(i=1, 2, …, m)
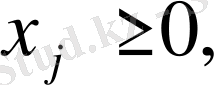 (j=1, 2, …, n),
(j=1, 2, …, n),
Онда осы шектеулер арқылы құрастырылған М аймағы 1-ширектегі n-өлшемді кеңістіктегі өлшемі n болатын дөңес көпжақты деп қарастыруға болады. Бұл жағдайда мақсат функциясы
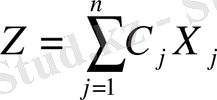
Z-дің кез-келген тұрақты мәнінде n-өлшемді гипержазықтық. Симплекс әдісінің мән-жайын тереңірек түсіну үшін алдыңғы тақырыптағы кейбір белгілі қағидаларды тағы да еске түсірейік. Мысалға, егер Z-дің мәні - ∞ тен + ∞ дейін өзгерсе, онда гипержазықтық өзіне-өзі параллель жылжи отырып, М дөңес көпжақтыға жетеді де, онымен бір нүктеде (немесе бір қабырғасының үстіне түседі) қиылысады, бұл нүкте «ену» нүктесі делінетіні алдыңғы тақырыпта айтылды. Гипержазықтықты және өзіне-өзін параллель етіп, М аймағы бойынша жылжыта берсек Z-дің бір мәнінде, ол гипержазықтық М аймағы соңғы нүктесімен жанасады да (бұл нүкте «шығу» нүктесі делінетіні белгілі), осыдан кейін М аймағынан шығып кетеді.
2. 4. Модельді жүзеге асырудағы таңдалған әдісті сипаттау
Сызықтық теңсіздіктердің геометриялық (графиктік) шешу жолы қарапайым сандық мысал бойынша қысқаша баяндалған. Осы түсініктерді кеңейте отырып, геометриялық жолмен сызықтық бағдарламалау есептерін шешу әдістерін қарастырайық. Мысалға, екі белгісізді m - теңсіздіктермен өрнектелген шектеулер жүйесімен сипатталған сызықтық бағдарламалау есебін берілсін. Оның моделінің жалпы түрі былай жазылады. Төмендегі шектеу шарттарын қанағаттандыратын:
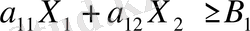
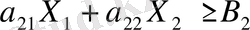
. . .
(3. 1)
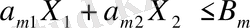
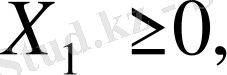
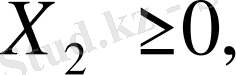 (3. 2)
(3. 2)
мына сызықтық мақсат функциясының
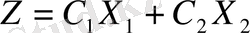 (3. 3)
(3. 3)
ең үлкен (ең кіші) мәнін табу керек. Бұл есепті график бойынша шешу үшін, ең алдымен бірінші теңсіздікті қарастырайық:
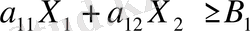 немесе
немесе
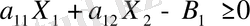
Егер
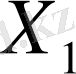 және
және
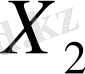 координат өрістері деп қарастырсақ, онда осы теңсіздік жазықтықта қандай аймақты құрады деген сұрау туады.
координат өрістері деп қарастырсақ, онда осы теңсіздік жазықтықта қандай аймақты құрады деген сұрау туады.
Бұл сұрауға жауап беру үшін, теңдеу
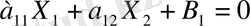 болатын Z түзуін құрамыз. Z түзуі барлық жазықтықты екі жарты жазықтыққа бөледі. (3. 1-суретте
болатын Z түзуін құрамыз. Z түзуі барлық жазықтықты екі жарты жазықтыққа бөледі. (3. 1-суретте
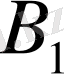 >0 болған жағдай көрсетілген) .
>0 болған жағдай көрсетілген) .
Ол жазықтың біреуі
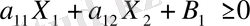 , ал екіншісі
, ал екіншісі
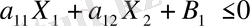 теңсіздіктерін орындайтын, ал түзуі бұл жазықтықтардың екеуінде де жатады деп қарастыруға боолады, өйткені екі теңсіздікте де қайсысы жоғары және төменгі жартылай жазықтықты береді. Егер
теңсіздіктерін орындайтын, ал түзуі бұл жазықтықтардың екеуінде де жатады деп қарастыруға боолады, өйткені екі теңсіздікте де қайсысы жоғары және төменгі жартылай жазықтықты береді. Егер
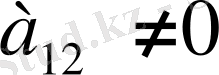 десек, онда берілген теңсіздіктерді былай жазуға болады:
десек, онда берілген теңсіздіктерді былай жазуға болады:
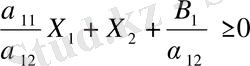
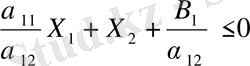 , бұлардан
, бұлардан
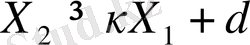 және
және
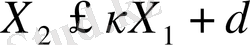 ,
,
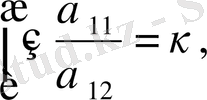
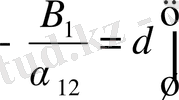 .
.
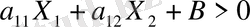
X
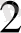
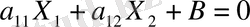
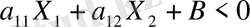
0 X
3. 1. -сурет
Бірінші жағдайда іздеп отырған жарты жазықтық Z түзуінен жоғары жатады
да, екішші жағдайда Z түзуінен төмен жатады. Ал егер
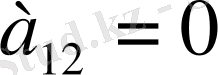 болса, онда қарастырып отырған теңсіздіктер
болса, онда қарастырып отырған теңсіздіктер
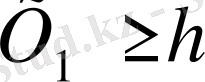 немесе
немесе
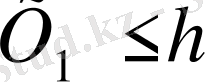 болып шығады да, X-h=0 сызығы Z түзуінің оң немесе сол жағында жатады.
болып шығады да, X-h=0 сызығы Z түзуінің оң немесе сол жағында жатады.
Мына теңсіздіктің қандай шарты қандай жазықтықты беретінін анықтайық:
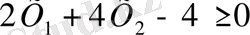
Шешуі.
Берілген теңсіздікті былай жазамыз:
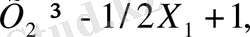 демек ол
демек ол
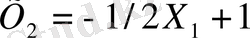 түзуімен оның жоғарғы жағында жататын жарты жазықтықты анықтайды (3. 1-сурет) . Көрсетілген тәсілмен қалған теңсіздіктердің графигін сызуға болады. Нәтижесінде, жарты жазықтықтардың қиылысуынан пайда болған (3. 1) және (3. 2) теңсіздіктердің шарттарын қанағаттандыратын геометриялық көпбұрыш құрылады. Осы көпбұрыштың барлық нүктелерінің координаттары (3. 1) және (3. 2) теңсіздіктердің шарттарын қанағаттандырады және осы есептің белгісіздерінің анықталу аймағы болып есептелінеді (3. 2- сурет(А) ) .
түзуімен оның жоғарғы жағында жататын жарты жазықтықты анықтайды (3. 1-сурет) . Көрсетілген тәсілмен қалған теңсіздіктердің графигін сызуға болады. Нәтижесінде, жарты жазықтықтардың қиылысуынан пайда болған (3. 1) және (3. 2) теңсіздіктердің шарттарын қанағаттандыратын геометриялық көпбұрыш құрылады. Осы көпбұрыштың барлық нүктелерінің координаттары (3. 1) және (3. 2) теңсіздіктердің шарттарын қанағаттандырады және осы есептің белгісіздерінің анықталу аймағы болып есептелінеді (3. 2- сурет(А) ) .
3. 2- сурет А-сурет
X
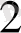 Equation. 3 X
Equation. 3 X
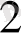 Equation. 3 L
Equation. 3 L
 Equation. 3
Equation. 3
. . . L
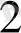
. . .
. . .
1 . . . M . . . L
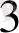

L
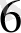 . . .
. . .
L
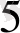 . . . L
. . . L
X
 X
X
0 1 2
Жазықтықты екі жарты жазықтыққа бөліп тұрған түзуді гипер түзуі деп
атайды. Гипер түзуі ретінде Z
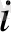 түзулерін қарастыруға болады. Есептің (теңсіздіктердің) анықталу аймағы кейде шектелмеуі де мүмкін (
Б, В
-суреттер) . Егер есепте мақсат функциясының максималды мәні іздестірілінсе, онда мұндай есептің анықталу аймағы жоғарғы жағынан шектелмеген, демек бұл аймақтарда мақсат функциясының максималды мәні болмайды.
түзулерін қарастыруға болады. Есептің (теңсіздіктердің) анықталу аймағы кейде шектелмеуі де мүмкін (
Б, В
-суреттер) . Егер есепте мақсат функциясының максималды мәні іздестірілінсе, онда мұндай есептің анықталу аймағы жоғарғы жағынан шектелмеген, демек бұл аймақтарда мақсат функциясының максималды мәні болмайды.
Қандай жағдай болмасын есептің шешімі болуы үшін, M аймағы шектеулі болуға тиіс. Аймақты құрайтын шектеуші шарттар сызықтық теңсіздіктер болғандықтан, M аймағының қабырғалары түзу сызық кесінділерінен тұрады. Сондықтан есептің анықталу аймағы M жазықтықта жатқан көпбұрыш.
Егер M аймағы барлық жағынан қоршалған (шектелген) аймақ болса, онда ол (3. 1) және (3. 2) теңсіздіктердің шешімін беретін аймақ деп есептелінеді.
Кейбір жағдайларда бірден барлық жарты жазықтықтарда жататын бір де нүкте табылмай қалуы мүмкін: былайша айтқанда, M аймағы «бос» жиын нүктелерінен тұрса, онда (3. 1) және (3. 2) теңсіздіктер жүйелері бір-біріне қарама -қайшы теңсіздіктер болып шығады (3. 4-сурет) .
M аймағының ерекше қасиеті- ол дөңес көпбұрышты бейнелейді. Осы себепті, дөңес көпбұрыш, яғни дөңес аймақ деп те айтылатынына тоқталайық.
Егер M аймағы кез келген екі А және В нүктесімен бірге сол А және В нүктелерін қосатын кесіндінің барлық нүктелерін қамтитын болса, онда M аймағы дөңес аймақ болады (3. 5-сурет а) . б) .
Берілген есептің анықтау аймағы қалай . Енді осы аймақта жатқан қандай нүкте мақсат функциясының оптималдық шешімі бола алатынын анықтайық. Былайша айтқанда, осы аймақта мақсат функциясының экстремалдық мәніқалай табылады. Бқл дөңес М аймақта жатқан бір нүкте, яғни табуымыз керек іздеп отырған мақсат функциясының экстремалдық (максималдық немесе минималдық) мәнін беретін осы нүктенің координатын. Егер мақсат функциясы (Z) тұрақты бір d санына тең десек
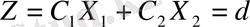 , онда сызықтық теңдеу аламыз, ал оның графигі түзу сызық болатынын білеміз. Егер жалпы түрде d санын
, онда сызықтық теңдеу аламыз, ал оның графигі түзу сызық болатынын білеміз. Егер жалпы түрде d санын
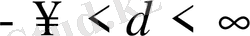 өзгерте берсек, онда
өзгерте берсек, онда
 түзу сызығы өзіне -өзі параллель бола отырып, бүкіл жазық аумағын сызып шығады (3. 6- сурет(а) ) .
түзу сызығы өзіне -өзі параллель бола отырып, бүкіл жазық аумағын сызып шығады (3. 6- сурет(а) ) .
Айталық М аймағы дөңес аймағы екен делік, ал мақсат функциясы өзіне -өзі параллель жылжи отырып, М аймағына жетсін. Бұл нүктені «ену» нүктесі деп, А арқылы белгілейік. Мақсат функциясы өзіне -өзі параллель жылжи отырып,
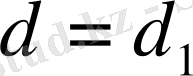 болғанда М аймағының В нүктесіне жетсін. Бұл В нүктені шартты түрде «шығу» нүктесі делік. 3. 6-cурет(б) бойынша Z мақсат функциясының ең кіші мәні А нүктесінде, ал ең үлкен мәні М аймағының В нүктесінде екендігі көрініп тұр.
болғанда М аймағының В нүктесіне жетсін. Бұл В нүктені шартты түрде «шығу» нүктесі делік. 3. 6-cурет(б) бойынша Z мақсат функциясының ең кіші мәні А нүктесінде, ал ең үлкен мәні М аймағының В нүктесінде екендігі көрініп тұр.
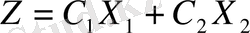 функциясы
функциясы
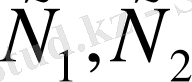 және
және
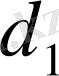 сандарына байланысты әртүрлі болып орналасуы мүмкін, міне, осыған байланысты кей кездерде Z функцияның графигі М аймағы мен бір нүктеде (3. 6- сурет(б) ) ғана қиылысуы мүмкін. Бұл жағдайда Z функцияның экстремалдық бір ғана мәні болады., ол мән
сандарына байланысты әртүрлі болып орналасуы мүмкін, міне, осыған байланысты кей кездерде Z функцияның графигі М аймағы мен бір нүктеде (3. 6- сурет(б) ) ғана қиылысуы мүмкін. Бұл жағдайда Z функцияның экстремалдық бір ғана мәні болады., ол мән
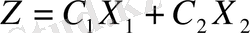 теңдеуіне сол қиылысу нүктелердің (А немесе В, б-сурет) координаттарыныңмәнін енгізу арқылы анықталады. (Мысалы,
теңдеуіне сол қиылысу нүктелердің (А немесе В, б-сурет) координаттарыныңмәнін енгізу арқылы анықталады. (Мысалы,
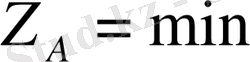 , ал
, ал
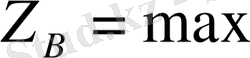 немесе керісінше) . Ал кей кездерде мақсат функциясы өзіне-өзі параллель жылжи отырып, М аймағының бір қабырғасының үстіне түсуі мүмкін (в- сурет) . Мысалы, 3. 6- суреттің (в) жағдайында
немесе керісінше) . Ал кей кездерде мақсат функциясы өзіне-өзі параллель жылжи отырып, М аймағының бір қабырғасының үстіне түсуі мүмкін (в- сурет) . Мысалы, 3. 6- суреттің (в) жағдайында
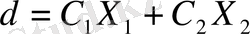 түзуі M аймағының AB қабырғасының бойында жататыны, бұл жағдайда Z мақсат функциясының кіші мәні шексіз, ал максималдық мән M аймағының D нүктесінде жалғыз болатындығы, ал 3. 7-суретте (a) оған керісінше жағдай бейнеленген.
түзуі M аймағының AB қабырғасының бойында жататыны, бұл жағдайда Z мақсат функциясының кіші мәні шексіз, ал максималдық мән M аймағының D нүктесінде жалғыз болатындығы, ал 3. 7-суретте (a) оған керісінше жағдай бейнеленген.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz