Квадрат теңдеулер

Жоспар

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .2
І.Квадрат теңдеулер және олардың түрлері
1.1.Квадрат теңдеулердің анықтамасы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .4
1.2.Толымсыз квадрат теңдеулер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..6
1.3. Квадрат теңдеулерді шешудің тәсілдері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..10
ІІ. Квадрат теңдеу түбірлерінің формуласы ... ... ... ... ... ... ... ... ... ... ... ... .15
2.1.Квадрат теңдеулерді пайдаланып есептер шығару ... ... ... ... ... ... ... ... ... ... ..16
2.2.Виет теоремасы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 21
Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .24
Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...25

Кіріспе

Мектептің математика курсында бастауыш сыныптардан бастап қаралатын ең негізгі буын алгебралық теңдеулерді шешу. Оқушылардың білімін білім стандарты талаптарына сай қалыптастыру үшін теңдеулерді шешу әдістерінің әрқайсын пайдалану жолдарын оқушыларға ғылыми негізде, нақты практикалық тұрғыда жеткізудің нәтижелі болатыны белгілі. Алгебралық теңдеулерді шешудің негізгі әдістері мына төмендегідей:
1) Теңбе-тең түрлендіру;
2) Айнымалыларды ауыстыру;
3) Көбейткіштерге жіктеу;
4) Мәндес теңдеулерге көшу.
Теңдеуді шешу жолдарын сан түрлі әдістермен жазып көрсетуге болады, алайда ескеретін жағдайлар бар. Орындалған теңбе-тең түрлендірулер математикалық тілде, математикалық символдарды пайдалана отырып мүмкіндігінше толық көрсетілуі керек. Ең негізгісі математикалық қате кетпесе, қажетті зертеулер жүргізілсе (анықталу обылысы, мәндерінің жиыны тағы сол сияқты), жауабы толық негізделіп берілсе жеткілікті. Жалпы мектеп курсындағы кез келген теңдеулерді шешу барысында үш жағдай кездеседі:
а) теңдеудің түбірлері болатын жағдай;
б) теңдеудің түбірлері болмайтын жағдай;
г) теңдеудің түбірлері шексіз сандар жиыны болатын жағдай. Осы үш жағдайдың үшінші жағдайына (теңдеудің түбірлері шексіз сандар жиыны болатын жағдай) мектеп курсында жеткілікті мән берілмейді. Соның салдарынан болу керек оқушылар көптеген қателіктерге жол береді, тіпті теңдеудің түбірлері қалайша шексіз сандар жиыны болады деген сұрақтарды да мұғалімге қояды. Өйткені оқушы тек қана теңсіздіктердің шешімдері шексіз сандар жиыны болады деп есептеледі. Демек, қосымша жұмыстар жүргізу қажет. Осы мәселеге байланысты оқушының білімін тереңдету үшін арнайы жасалған жұмыстарды көбірек қолдану керек.
Математиканың тарихи даму барысында әр қырына, түрінше шешімін тауып отырған ең басты мәселелердің бірі-сан ұғымын дамыту болды. Сан ұғымын кеңейту мәселесі алгебра ғылымының өз алдында бөлініп дербес даму жолына түсуін күрт жеделдетті, шешуі болатын теңдеулер класын көбейтті, қолданыстағы сандар арсеналын байытуды, кеңейтуді талап етті. Алгебра иррационалдықтың, яғни иррационал сандардың рационал сандармен тең енгізілуі осы қажеттіліктің көрінісі екені белгілі.
Теңдеулерді шешу қиын есептерді шешуді жеңілдетеді. Есепті шешу үшін есептің шарты баяндалған математикалық тілді математикалық модель-өрнекті құру үшін белгісізді х, у, z деп белгілеп, шартта баяндалған барлық жағдайды еске алып өрнек теңдеу құрамыз. Ары қарай осы өрнектен белгісізді табу теңдеуді шешу болып табылады.
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
Бұл курстық жұмыс алгебра курсында қарастырылатын квадрат теңдеулерге және оларды шешу жолдарының әр түрлі әдістеріне негізделініп отыр.
«Квадрат теңдеулер» мектептегі алгебра курсының маңызды тақырыптарының бірі. Көптеген табиғи үдірістер мен құбылыстар, с.с. мазмұнды есептердің шығарылуы квадрат теңдеулерді шешуге келіп тіреледі. Теңсіздіктерді шешу, функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін, өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді табу есептерін шығару және т.б. жағдайларда квадрат теңдеулерді шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық, көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада, геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат теңдеулерге келтіріледі.

Пайдаланылған әдебиеттер

1. Қазақстан Республикасы жалпы орта білім берудің мемлекеттік жалпыға міндетті стандарттары. Жалпы орта білім. – Алматы: РОНД, 2002. –360 бет.
2.Математика және Физика, 2004 №5
3. Алгебра – 8, Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.,
Суворова С.Б. Алматы, Рауан, 1992 – 256 бет.
4. Математика және Физика, 2004 №1
5. Алгебра – 8, Медеуов Е., Базаров Қ., Балтаев Б. Атамұра 2005 ж.
6. Теляковский С.А. Алгебра – 8. Орта мектептің 8-класына арналған
оқулық, Алматы, «Рауан» 1992 ж.
7. Брадис В.М. Четырехзначные математические таблицы для
средней школы. изд. 57-е. – М. Просвещение. 1990. с. 83
8. М. Математика. №№ 21/96, 27/97, 10/97, 18/98, 21/98.
9. Окунев А.К. Квадратичное функций уравнения и неравенство,
пособия для учителя – М. Просвещение. 1972.
10. Көбесов А. Математика тарихы, Алматы «Қазақ университеті»
1993.
11.Көбесов А. Математика тарихы.Алматы «Қазақ университеті» 1993.
12.Математика және физика журналы №2 2003
13.Математика және физика журналы №1 2004
14.Алгебра 8 сынып Ә.Н.Шыныбеков Алматы «Атамұра 2012 ж»

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 25 бет
Таңдаулыға:

Жоспар

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...2
І.Квадрат теңдеулер және олардың түрлері
1.1.Квадрат теңдеулердің анықтамасы ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... .4
1.2.Толымсыз квадрат теңдеулер ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... .6
1.3. Квадрат теңдеулерді шешудің тәсілдері ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... 10
ІІ. Квадрат теңдеу түбірлерінің формуласы ... ... ... ... ... ... .. ... ... ... ... ... ...15
2.1.Квадрат теңдеулерді пайдаланып есептер шығару ... ... ... ... ... ... ... . ... ... ... .16
2.2.Виет теоремасы ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 21
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .24
Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ...25

Кіріспе

Мектептің математика курсында бастауыш сыныптардан бастап қаралатын ең негізгі буын алгебралық теңдеулерді шешу. Оқушылардың білімін білім стандарты талаптарына сай қалыптастыру үшін теңдеулерді шешу әдістерінің әрқайсын пайдалану жолдарын оқушыларға ғылыми негізде, нақты практикалық тұрғыда жеткізудің нәтижелі болатыны белгілі. Алгебралық теңдеулерді шешудің негізгі әдістері мына төмендегідей:
1) Теңбе-тең түрлендіру;
2) Айнымалыларды ауыстыру;
3) Көбейткіштерге жіктеу;
4) Мәндес теңдеулерге көшу.
Теңдеуді шешу жолдарын сан түрлі әдістермен жазып көрсетуге болады, алайда ескеретін жағдайлар бар. Орындалған теңбе-тең түрлендірулер математикалық тілде, математикалық символдарды пайдалана отырып мүмкіндігінше толық көрсетілуі керек. Ең негізгісі математикалық қате кетпесе, қажетті зертеулер жүргізілсе (анықталу обылысы, мәндерінің жиыны тағы сол сияқты), жауабы толық негізделіп берілсе жеткілікті. Жалпы мектеп курсындағы кез келген теңдеулерді шешу барысында үш жағдай кездеседі:
а) теңдеудің түбірлері болатын жағдай;
б) теңдеудің түбірлері болмайтын жағдай;
г) теңдеудің түбірлері шексіз сандар жиыны болатын жағдай. Осы үш жағдайдың үшінші жағдайына (теңдеудің түбірлері шексіз сандар жиыны болатын жағдай) мектеп курсында жеткілікті мән берілмейді. Соның салдарынан болу керек оқушылар көптеген қателіктерге жол береді, тіпті теңдеудің түбірлері қалайша шексіз сандар жиыны болады деген сұрақтарды да мұғалімге қояды. Өйткені оқушы тек қана теңсіздіктердің шешімдері шексіз сандар жиыны болады деп есептеледі. Демек, қосымша жұмыстар жүргізу қажет. Осы мәселеге байланысты оқушының білімін тереңдету үшін арнайы жасалған жұмыстарды көбірек қолдану керек.
Математиканың тарихи даму барысында әр қырына, түрінше шешімін тауып отырған ең басты мәселелердің бірі-сан ұғымын дамыту болды. Сан ұғымын кеңейту мәселесі алгебра ғылымының өз алдында бөлініп дербес даму жолына түсуін күрт жеделдетті, шешуі болатын теңдеулер класын көбейтті, қолданыстағы сандар арсеналын байытуды, кеңейтуді талап етті. Алгебра иррационалдықтың, яғни иррационал сандардың рационал сандармен тең енгізілуі осы қажеттіліктің көрінісі екені белгілі.
Теңдеулерді шешу қиын есептерді шешуді жеңілдетеді. Есепті шешу үшін есептің шарты баяндалған математикалық тілді математикалық модель-өрнекті құру үшін белгісізді х, у, z деп белгілеп, шартта баяндалған барлық жағдайды еске алып өрнек теңдеу құрамыз. Ары қарай осы өрнектен белгісізді табу теңдеуді шешу болып табылады.
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
Бұл курстық жұмыс алгебра курсында қарастырылатын квадрат теңдеулерге және оларды шешу жолдарының әр түрлі әдістеріне негізделініп отыр.
Квадрат теңдеулер мектептегі алгебра курсының маңызды тақырыптарының бірі. Көптеген табиғи үдірістер мен құбылыстар, с.с. мазмұнды есептердің шығарылуы квадрат теңдеулерді шешуге келіп тіреледі. Теңсіздіктерді шешу, функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін, өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді табу есептерін шығару және т.б. жағдайларда квадрат теңдеулерді шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық, көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада, геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат теңдеулерге келтіріледі.

І.Квадрат теңдеу және оның түрлері.
1.1.Квадрат теңдеулердің анықтамасы

ax + ax2 + c = 0, a != 0 түріндегі теңдеулерді квадраттық теңдеу деп атайды. Мұндағы х-айнымалы шама, а,в,с нақты сандар, әрі а-екінші дәрежелі мүшенің коэффициенті, в-бірінші дәрежелі мүшенің коэффициенті, с-бос мүше. ax2 + bx + c = 0 квадраттық теңдеуінде коэффициенттерінің бірі - в не с немесе в мен с- ның екеуі де нөлге тең болса,ондай теңдеулерді толымсыз квадраттық теңдеу деп атайды.

1) в = c = 0 болса, онда ax[2] = 0; шешуі: х = 0
2) c = 0, b != 0 болса, онда ax[2] + bx = 0; шешуі : x (ax + b) = 0; х = 0; x= - ba
3) с != 0, b = 0 болса, онда ax[2] + c = 0; шешуі : x[2][ ]=; егер - ca = 0 болғанда
Мысал: Ауданы 6 м2 тіктөртбұрыш пішінді жер телімін қоршау керек болсын.
Жер телімінің бір қабырғасы (ұзындығы) қоршау бар жақтан өтеді. Егер қоршауға
арналған материалдың ұзындығы 8 м ғана болса, онда тіктөртбұрышты жер
телімінің ені қандай болу керек?
Шешуі: Ені - х м.
Ұзындығы - (8-2х) м2
х*(8-2х)= 6
2х-8х+6 =0
х2-4х+3 =0
х2=4х-3ху
х2, у 4х-3 болатын екі функция қарастырылады.
Демек, теңдеудің екі шешімі бар. Есептің шартын х 1 мәні ғана
қанағаттандырады. Сонымен, жер телімінің ені 1м, ал ұзындығы сәйкесінше 6м.
Есеп шығару барысында жаңа х2-4х+3 0 теңдеуі қарастырылды.

Анықтама: ах2+вх+с 0 =(1)
түрінде берілген теңдеу квадрат теңдеу деп аталады.
Мұндағы а,в,с-нақты сандар және а 0, ал х-айнымалы. (1) теңдеудегі а-
бірінші коэффициент, в-екінші коэффициент, с-бос мүше.
Егер (1) теңдеудегі в 0 және с 0 болса, онда ол теңдеу толық квадрат
теңдеу деп аталады.
Мысалы: х2-2х-1= 0, 3х2-8х+5= 0, 2,1х2+102,3х+0,8 =0 толық квадрат
теңдеулер.в немесе с, немесе в мен с нөлге тең болатын дербес жағдайлардағы квадраттеңдеу толымсыз квадрат теңдеу деп аталады.
Толымсыз квадрат теңдеулер былай жазылады:
ах2+вх= 0 (мұндағы с 0);
ах2+с= 0 (мұндағы в 0);
ах2=0 (мұндағы в 0, с 0).
Егер толық квадрат теңдеудегі бірінші коэффициент 1-ге тең (а 1) болса, ондаол келтірілген квадрат теңдеу деп аталады.
Келтірілген квадрат теңдеу
х2+рх+q =0
түрінде жазылады. Мұндағы р жәнеq - кез келген нақты сандар.Енді толымсыз квадрат теңдеулердің шығарылуын қарастырайық.
ах2+вх= 0, мұндағы а 0
шешу жолын келтірейік.
х(ах+в) 0
теңдеуін аламыз.
х1 =0 және х2 =- ba болатын екі түбірі болады.
1-мысал:
6х2-3х= 0 теңдеуін шешейік.
х(6х-3)= 0
х1 =0, 6х-3 =0 х2 = 36 = 12; Жауабы: 0; 12.
Енді ах2+с= 0, мұндағы а 0!= (4) толымсыз квадрат теңдеуінің шешімін
қарастырайық. Бұл теңдеудің екі жағын а-ға бөлеміз.
х2=-ca- (5)
теңдеуін аламыз.
1-жағдай: а және в сандарының таңбалары бірдей, онда caоң сан, - caтеріс сан
болады. х2=0 екені белгілі,сондықтан ол теріс санға тең болуы мүмкін емес.
Теңдеудің шешімі болмайды.

2-жағдай: с= 0 болсын. х2=0 теңдеуіне көшеді.Теңдеудің бір ғана х =0 шешімі
бар.
3-жағдай: а және с сандарының таңбалары қарама-қарсы (яғни, біреуі оң,
екіншісі теріс сан). Бұл жағдайда х2=- - caтеңдеуінің х 1,2 +- ca екі түбірі болады.
2- мысал: 4х2-9= 0 теңдеуін шешейік.4х2= 9
х2=94; х1=32 ; х2=- 32. Жауабы: 32 ; - 32.;
3-мысал: 5х2-8=7х2-8 теңдеуін шешейік.
5х2-8-7х2+8=0
-2х2=0
х2=0
1.2.Толымсыз квадрат теңдеулер.

Толымсыз квадраттық теңдеулердің түрлері
* ах2+с=0 мұндағы с!=0
* ах2+вх=0 мұндағы в!=0
* ах2=0

1. ах2+с=0 мұндағы с!=0

екі түбірі болады
түбірі жоқ

2. ах2+вх=0 мұндағы в!=0

немесе

екі түбірі болады.

3.ах2=0

бір ғана түбірі болады.
Мысалы:
5х2+4х=0
-õ2+3=0
Õ1=-√3
Екі түбірі болады

х(5х+4)=4
х=0 немесе 5õ+4=0
5õ=-4
õ=-45
екі түбірі болады.
7õ2=0
Х2=0
х=0
бір ғана түбірі болады

теңдеудің екі жағын да а -ға бөліп, онымен мәндес болатын келтірілген квадраттық теңдеу шығарып аламыз

Осы теңдеуді түрлендірейік:

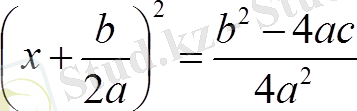
теңдеуі

теңдеуімен мәндес.

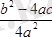
Мұның түбірінің саны бөлшегінің таңбасына
тәуелді болады.а!=0 болғандықтан ,4а2 - оң сан болады,сондықтан бұл бөлшектің таңбасы оның алымының, яғни b2-4ас өрнегінің таңбасымен анықталады.

Осы өрнекті квадраттықтеңдеуінің дискриминанты деп атайды. Мұны D әрпіменбелгілейді, яғни 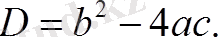Енді екінші теңдеуді мына түрде жазамыз:

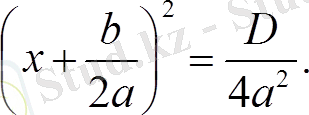
Енді D-ға тәуелді мүмкін болатын әр түрлі жағдайларды қарастырайық.
Егер D › 0 ,онда

Сонымен, бұл жағдайда теңдеуінің екі түбірі болады:

Қысқаша былай жазуға болады:

мұны квадраттық теңдеудің түбірлерінің формуласы деп атайды .

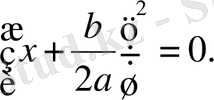Егер D =0 болса,онда

бұдан

бұл жерде теңдеуінің бір түбірі болады.

Егер D 0 болса онда бөлшегінің мәні теріс болады сондықтан

теңдеуінің түбірлері жоқ.
Онда теңдеудің де түбірлері жоқ болады.
Сонымен,
D 0 екі түбір болады
D=0 бір түбірі болады
D0 түбірі жоқ
1 мысал

Жауабы:

2-мысал:

Жауабы:х=6

3-мысал

Жауабы:түбірлері жоқ
1.3.Квадрат теңдеулерді шешудің тәсілдері

Көптеген табиғи процестер мен құбылыстар квадрат теңдеулер арқылы сипатталады, мазмұнды есептердің көбісінің шешуі квадрат теңдеулерді шешуге келіп тіреледі.Квадрат теңдеулерді оның түбірлерінің формуласы бойынша шешу тақырыбымен 8-сынып алгебра курсында таныстым. Бұл тақырып маған жаңа тақырып әрі қызықты болды. Сондықтан осы тақырып бойынша квадрат теңдеулерді шешу әдістерін өздігімнен іздендім. Дегенмен, квадрат теңдеулерді шешудің басқа да әдіс-тәсілдері бар. Осы әдіс-тәсілдерді қарастыру арқылы бұл тақырып туралы терең білуге болады. Кейбір әдістерді тиімді жолдың бірі ретінде есептерді шығаруда қолдануға болады. Вавилондықтар (б.з.д екі мыңыншы жылдар шамасында) толымсыз квадрат х2+-х=а шеше білген. Вавилондықтардың квадрат теңдеуін шешу жолы қазір біз қолданып жүрген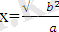формуласына пара-пар.Вавилондықтар мұнан басқа да

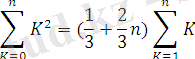
Формулаларын және басқа арифметикалық прогрессиялардың қосындысын табудың ережелерін білген. 1945 жылы вавилондықтардан қалған тағы бір математикалық мәтіннің мазмұны анықталады.Мұнда қабырғалары рационал сандар болып келген тік бұрышты үшбұрыштың тізімі келтірілген, яғни 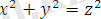теңдеуін қанағаттандыратын пифагор сандарын табу жолы қарастырылған.
Пифагор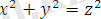анықталмаған теңдеуінің бүтін шешуін, яғни қазіргіше айтқанда: пифагор сандарын табу ережесін қалдырған. Олар мынадай формулалармен анықталады:
мұнда тақ сан
Ежелгі грек математиктері квадрат теңдеулердің кейбір түрлерін шешуді геометриялық салуларға келтіріп шеше білген.
Квадраттың диагоналы АС-мен оның қабырғасы өлшемдес болсын деп кері жориық.Онда 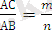бұдан қысқармайтын бөлшек шығады, мұнда m,n-тақ сандар.
Пифагор теоремасы бойынша 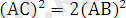, олай болса, , ендеш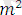е, және жұп сан, 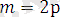түріндегі сан болады. Бұдан 4р2=2n2 немесе n2=2р2 ендеше,n2, n-жұп сан болады деген қорытынды шығады. Сөйтіп,m -әрі ортақ,әрі жұп сан. Бұл мүмкін емес. Олай болса, квадраттың диагоналы оның қабырғасымен өлшемдес болмайды
Осы сияқты гректер 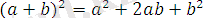тәріздес алгебралық формулаларды да геометрия тілімен баяндай білген.
Геометриялық алгебраның жәрдемімен көптеген квадрат теңдеуге келтіретін есептерді шешуге болатын еді. Ол теңдеулер эллипстық, гиперболалық және параболалық болып үш тілге бөлініп, осылардың әрқайсысынан шешудің бірыңғай жалпы әдістері жасалады.
1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу
Мысал: х2+4х+3 =0 теңдеуін шешейік.
Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:
х2+х+3х+3 =х(х+1)+3 (х+1) =(х+1)(х+3)
Демек, теңдеуді былай жазуға болады: (х+1)(х+3) =0
Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х=-1сандары х2+4х+3=0 теңдеуінің түбірлері болып табылады.
2-әдіс. Толық квадратқа келтіру әдісі
Мысал: х2+8х-9=0 теңдеуін шешейік.
Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х2+8х өрнегін төмендегідей жазып аламыз: х2 + 8х=х2+2х4
Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 4-тің екі еселенгені. Толық квадрат алу үшін 42-ын қосу керек. Сонда х2+2х4+42=(х+4)2
Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 42-ын қосып, алып тастаймыз. Сонда шығатыны: х2+8х-9=х2+2х4+42-9-4=(х+4)2-25Соны мен, берілген теңдеуді былайша жазуға болады: (х+4)2-25=0 , яғни (х+4)2=25.
Бұдан х+4=5,х=1 немесе х+4=-5, х=-9
Жауабы: 1;-93-әдіс. Квадраттық теңдеулерді формула арқылы шешу
ах2+вх+с=0, а!=0 теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі өрнекті аламыз:
4а2х2+4ахв+4ас=0
((2ах)2+4ахв+в2)-в2+4ас=0 , (2ах+в)2=в2-4ас
2ах+в=2ах = -в х=1
Оған келесідегідей мысалдар келтіруге болады:
1)3х2-7х+4=0 теңдеуін шешейік.
а=3, в=-7, с=4. Д=в2-4ас=(-7)2-4::4::3=49-48=1.
Д0 болғандықтан, екі әр түрлі түбір болады: х1=1, х2=-1
Сонымен, дискриминант оң болғанда, яғни в2-4ас0, ах2+вх+с=0 теңдеуінің екі түрлі түбірі болады.
2)9х2+6х+1=0 теңдеуін шешейік.
а=9, в=6, с=1. Д=в2-4ас=62-4::9::1=0.
Д=0 болғандықтан, бір ғана түбір бар болады: х= 1, х= -1
Сонымен, егер дискриминант нөлге тең болса, яғни в2-4ас=0, ах2+вх+с=0 теңдеуінің жалғыз
түбірі бар болады: х=1
3)х2+2х+3=0 теңдеуін шешейік.
а=1, в=2, с=3. Д=в2-4ас=4-4::3::1= -8.
Д0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды.
Сонымен, егер дискриминант теріс болса, яғни в2-4ас0, онда ах2+вх+с=0 теңдеуінің түбірі болмайды. 4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешу
Келтірілген түбірлері Виет теоремасын қанағаттандырады.
Ол былай беріледі: а=1 болғанда,
Бұдан келесі тұжырымдарды шығаруға болады:
а) Егер q (1) теңдеудің бос мүшесі оң болса (q 0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р0, онда екі түбірі де теріс болады, егер р0, онда түбірлері оң болады.

Мысал, 1)х2-9х+20=0, х1=4, х2=5, мұнда q=20 0, р=-9 0;
2)х2+5х+6 =0, х1 =-2, х2 =-3, мұнда q =6 0, р =5 0.
б) Егер q (1) теңдеудің бос мүшесі теріс болса (q 0), онда теңдеудің екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң болады, егер р 0 болса, теріс болады, егер р 0. Мысал, 1) х2+3х-4 =0; х1 =-4, х2 =1 мұнда q =-4 0, р=-3 0
2) х2-7х-8 =0; х1 =8, х2 =-1 мұнда q =-8 0, р =-7 0
5-әдіс. Теңдеуді асыра лақтыру әдісімен шешу
ах2+вх+с =0 , а !=0 квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз: а2х2+авх+ас=0. ах =у деп белгілесек, х = . Олай болса у2+ву+ас =0 теңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у1, у2 - ні Виет теоремасы арқылы табамыз. Соңында х1 = , х2 = -ны аламыз. Бұл жағдайда а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті асыра лақтыру әдісі деп атайды . Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.
Мысал: 2х2-9х+9=0 теңдеуін шешейік.
Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде
у2-9у+18=0 теңдеуін аламыз. Виет теоремасы бойынша
Жауабы: 3; 1, 5.
6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану
ах2+вх+с=0, а!=0 квадрат теңдеуі берілген.
Егер а+в+с=0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х1=1, х2=
Мысал: 7+2-9=0 қосындысы 0-ге тең. Осы үш сан үшін квадрат теңдеу құрастырып, оны шешейік:
7-әдіс. Квадрат теңдеуді циркуль және сызғыш көмегімен шешу ах2+вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен шешу әдісін ұсынамыз (1-сурет). Ізделінді шеңбер абцисса өсінде В(х ;0) және Д (х2;0) нүктелерінде қиылыссын делік. Мұндағы х1, х2 - ах2 + вх + с=0 теңдеуінің түбірлері және ординат осінен А(0;1) және С(0; ) нүктелері арқылы өтеді делік. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.