Тізбектер мен функциялардың шектері: анықтамалар, қасиеттер және негізгі теоремалар


Жоспар
Кіріспе . . . 2
І. Тізбектің шектері.
1. 1. Тізбек және тізбектің шегі . . . 3
1. 2. Тізбек шегінің анықтамасы . . . 4
ІІ. Шегі бар тізбектердің қасиеттері(жинақталған тізбектер) .
2. 1. Шенелген және шенелмеген тізбектер . . . 8 2. 2. Жиынтықты тізбектер және олардың негізгі қасиеттері . . . 10
2. 3. Функцияның шегі . . . 12
2. 4. Тізбектерге арифметикалық амалдар қолдану . . . 19
ІІІ. Монотонды тізбектер.
3. 1. Монотонды тізбектердің анықтамасы. Негізгі теорема . . . 20
3. 2. Функцияның монотонды болуының белгілері . . . 24
Қорытынды . . . 28
Әдебиеттер . . . 29
Кіріспе
Білім - болашақ бағдары, кез-келген маман даярлайтын оқу орынның басты міндеттерінің бірі - жеке тұлғаның құзіреттілігін дамыту. Құзірет - оқушының жеке және қоғам талаптарын қанағаттандыру мақсатындағы табысты іс-әрекетіне қажетті білім дайындығына әлеуметтік тапсырыс. Құзыреттілік - оқушының әрекет тәсілдерін жан-жақты игеруінен көрінетін білім нәтижесі. Ақпараттық құзыреттілік - бұл жеке тұлғаның әртүрлі ақпаратты қабылдау, табу, сақтау, оны жүзеге асыру жәнеақпараттық - коммуникациялық технологияның мүмкіндіктерін жан-жақты қолдану қабілеті. Оқушылардың түпкілікті құзіреттіліктері - білім берудің жаңа нәтижелер. Құзіреттілікті оқушының пән бойынша игерген білім, білігінің жинағы деп қабылдауға келмейді. Ол - оқу нәтижесінде өзгермелі жағдайда меңгерген білім, білік, дағдыны тәжірибеде қолдана алу қабілеті болып табылатын жаңа сапа. Ақпараттық құзіреттілікті қалыптастырудың басты мақсаты - оқушыларды ақпаратты беру, түрлендіру және оны қолдану білімдерімен қаруландыру, олардың компьютерлік технологияны өз қызметтеріне еркін, тиімді пайдалана алу қабілеттерін қалыптастыру.
Оқушылар үшін математика - бұл ойлау әдісі, сондықтан болашақ математиктердің қоршаған ортаны қабылдауында математикалық комплекстің пайдасы өте көп. Математика тараулары мен қолданбалы есептерді шығару алда негізгі пәндерді жақсы меңгеруге септігін тигізеді. Математикалық анализ, алгебра және геометрия пәндері сияқты жоғарғы дәрежелі кадрлар даярлауда қажетті пән болып табылады. Тізбектің шегі тарауы математикада әртүрлі қолданылуларында маңызды орын алады. Тізбек ұғымы, жалпы шек ұғымы, оқушылардың түсініп, меңгеруіне аса күрделі тақырыптардың бірі. Курстық жұмыстың мазмұнында математиканың негізгі тарауларының бірі - тізбектің шегі толық қамтылған. Негізгі анықтамалар мен теоремалардың мағынасын ашатын мысалдар мен ескертулер көптеп келтірілген.
І. Тізбектің шектері.
1. 1. Тізбек және тізбектің шегі.
Натурал сандар жиынында анықталған функциясы тізбек деп аталады. n натурал санына сәйкес ƒ функциясының мәні х n , деп белгіленеді, яғни ƒ (n) =х п .
Тізбектің мәні, яғни х n тізбектің мүшелері деп аталады.
Тізбекті былайша белгілейміз: х 1 , х 2 , . . . , х n, . . . ;
х 1 , х 2 . . . ;
{ х n } ∞ n=1 х;
{х n }
{х n }, n ≥ 1 ;
n → x n (n = 1, 2, . . . ) ;
→x n ;
Қысқаша, «тізбек { х n } ∞ n=1 х; », деген сөзді «х п тізбегі» деп айтамыз. Егер тізбек қасиеттері арқылы берілсе (мысалы, жинақтылық немесе монотондық т. б. ), онда (1) белгілеу қолданылады. Тізбекті анықтау үшін төмендегідей тәсілдер пайдаланылады:
1°. х п -ді тікелей табу ережесі қолданылады.
Мысалы, хп = 1(n=1, 2, . . . ) ;
х п = n 2 +4 п +3 (п= 1, 2, . . . ) ;
х п = п (п= 1, 2, . . . ) ; т. б . . .
2°. х п -ді жанамалап табу ережесі арқылы, мысалы, x 1 =x 2 =l, х п =х n -1 +х п -2 (п=3, 4, . . . ), (2) рекурренттік формула(к=2) . яғни 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . - бұл Фибоначчи тізбегі. Берілген тізбектің алғашқы к мүшелері арқылы тізбектің n-ші мүшесін табу формуласын шығару үшін (к - натурал сан) қолданылатын формула рекуренттік формула деп аталады, (recurrence - лат. «қайта оралу») .
3°. Тізбектің мүшелерін табу үшін ережені сөзбен көрсетуге болады, мысалы, хп - жай сан, яғни 1, 3, 5, 7, 11, . . .
4°. Алғашқы мүшелерінің берілуі арқылы;
Мысалы, 1, , тізбегінде жалпы мүше x n = тең болады.
1. 2. Тізбек шегінің анықтамасы.
Тізбек және оның шегі ұғымдары математиканың ішкі проблемаларымен қатар оны қолдану жолдарында пайда болады. Мысалы, біз үшбұрыштың ауданының анықтамасын және оны есептеу жолын біле тұра, радиусы R-ге тең дөңгелектің ауданы деген не және оны қалай табуға болады деген сұрақта қарастырайық.
Әрбір n ≥ 2 үшін радиусы R-ға тең дөңгелекке 2 n бұрышты дұрыс көпбұрыш Sn -ді іштей сызсақ, онда олардың аудандары хп тізбегін құрайды. Бір жағынан п өскен сайын Sn фигурасы дөңгелекке ақырсыз жақындай түседі, екінші жағынан кез келген п үшін Sn фигурасы дөңгелекпен дәл беттеспейді. Онда дөңгелектің ауданы дегеніміз не?
Бұл сұраққа жауап беру үшін тізбектің шегі ұғымын енгізуіміз қажет. Шек ұғымының негізі мағынасы мынада: номері өскен сайын тізбектің мүшелері қандай да бір санға ақырсыз жақындайды. Сол санды тізбектің шегі деп аталады.
Анықтама
. Егер бізге қалағанымызша аз e оң саны берілсе және айнымалы шама
 -тің бір мәнікөрсетіліп, одан кейінгі мәндерінің бәрі мына
-тің бір мәнікөрсетіліп, одан кейінгі мәндерінің бәрі мына
теңсіздікті
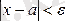 қанағаттандырса, түрақты
қанағаттандырса, түрақты
 саны айнымалы
саны айнымалы
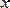 тің шегі
тің шегі
делінеді де, былайша жазылады:
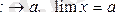 Сандар тізбегі
Сандар тізбегі

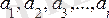 үшін бұл анықтаманы былайша айтуға болар еді. Егер де алдын ала кез келген аз eоң саны берілсе,
үшін бұл анықтаманы былайша айтуға болар еді. Егер де алдын ала кез келген аз eоң саны берілсе,
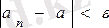 теңсіздігі
теңсіздігі
 нөмірден бастап орындалатын болса, онда түрақты сан
нөмірден бастап орындалатын болса, онда түрақты сан
 -ны тізбектің шегі дейді де
-ны тізбектің шегі дейді де
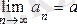 cимволымен жазады. Мұндағы lіm латын тіліндегі lіmes (шек) деген сөзден қысқартылып алынған. Бұл жағдайды былайша:
cимволымен жазады. Мұндағы lіm латын тіліндегі lіmes (шек) деген сөзден қысқартылып алынған. Бұл жағдайды былайша:
 тізбегі түрақты
тізбегі түрақты
 санына ұмтылады деп те айтады және былай жазады:
санына ұмтылады деп те айтады және былай жазады:

 ; тізбекті
; тізбекті
 санына жинақталады деп те атайды.
санына жинақталады деп те атайды.
Мысалы. 1) жалпы мүшесі
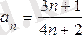 түрінде берілген сан тізбегі өзінің шегі
түрінде берілген сан тізбегі өзінің шегі
 -ке ұмтылады.
-ке ұмтылады.
Шынында, алдын ала
 санын алып,
санын алып,
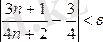 теңсіздігі
теңсіздігі
 номерінің қай мәнінен бастап орындалатынын анықталық. Бұл теңсіздікті мына түрге түрлендіреміз
номерінің қай мәнінен бастап орындалатынын анықталық. Бұл теңсіздікті мына түрге түрлендіреміз
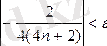 бұдан
бұдан
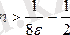 .
.
Демек,
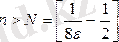 болғанда, анықтамаға сәйкес
болғанда, анықтамаға сәйкес
 қарастырылып отырған тізбектің шегі болады.
қарастырылып отырған тізбектің шегі болады.
2) Тізбектің жалпы мүшесі былай
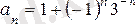 берілсе, бұл тізбектің шегі бірге тең.
берілсе, бұл тізбектің шегі бірге тең.
Шынында,
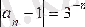 кез-келген e>0үшін
кез-келген e>0үшін
 теңсіздігі
теңсіздігі
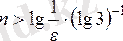 болғанда орындалады.
болғанда орындалады.
Бұдан кез келген тізбектің шегі болады деген ұғым тумауы керек.
Мысалы. Тізбектің мүшелері мына формулалармен берілсе
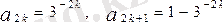
мұнда k-ның үлкен номерлерінен бастап, жұп номерлі мүшелерінің нольден айырмашылығы керегінше аз болады да, тақ номерлері мүшелерінің бірден айырмашылығы аз болады. Сондықтан тізбектің шегі болмайды.
Анықтама. Егер алдынала берілген әрбір оң сан М үшін айнымалы
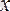 -тің бір мәнікөрсетіліп және кейінгі мәндерінің бәрі мына теңсіздікті
-тің бір мәнікөрсетіліп және кейінгі мәндерінің бәрі мына теңсіздікті
 қанағаттандырса,
қанағаттандырса,
 шексіздікке ұмтылады дейміз. Бұндай айнымалы шаманы шексіз үлкен айнымалы шама деп,
шексіздікке ұмтылады дейміз. Бұндай айнымалы шаманы шексіз үлкен айнымалы шама деп,
 cимволымен белгілейді.
cимволымен белгілейді.
Мысалы.
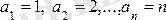 тізбегі шексіздікке ұмтылады.
тізбегі шексіздікке ұмтылады.
e саны.
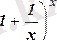 функциясының
функциясының
 шегі
шегі
Жалпы мүшесі
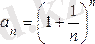 түрінде берілген сан тізбегінің шегін
e
саны деп атайды, яғни
түрінде берілген сан тізбегінің шегін
e
саны деп атайды, яғни
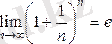 .
e-саны иррационал сан және оның жуық мәні мынадай e=2. 71828128 . . .
.
e-саны иррационал сан және оның жуық мәні мынадай e=2. 71828128 . . .
Теорема.
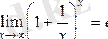 . (**)
. (**)
(**) -формуласын 2-ші тамаша шек деп атайды.
Егерде (**) формулада
 десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:
десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:
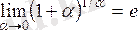 . e-cанын пайдаланып шығарылатын кейбір шектерді келтірейік:
. e-cанын пайдаланып шығарылатын кейбір шектерді келтірейік:
1)
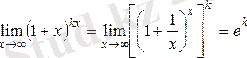 .
.
2)
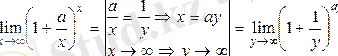 e
e
 .
.
3)
 .
.
3')
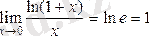 .
.
4)
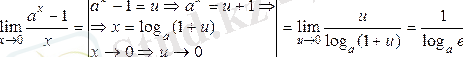
5)

6)
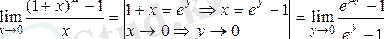
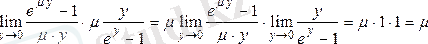
Егерде
 шегін
шегін
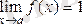 және
және
 болған жағдайда есептеп шығару керек болса, онда
болған жағдайда есептеп шығару керек болса, онда
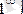 түріндегі анықталмағандық алар едік.
түріндегі анықталмағандық алар едік.
Бұл секілді анықталмағандықтарды ашу үшін, берілген функцияның
 негізі мен дәреже көрсеткішін мына формуланы
негізі мен дәреже көрсеткішін мына формуланы
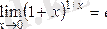
қолдану мүмкін болатындай етіп түрлендіру керек .
Мысалы.
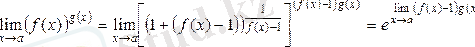 .
.
Осыдан,
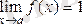 ,
,
 жағдайда, мына формула табылады
жағдайда, мына формула табылады
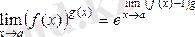 (бұл жерде үзіліссіз функциялардың композициясының үзіліссіздігі пайдаланылды) .
(бұл жерде үзіліссіз функциялардың композициясының үзіліссіздігі пайдаланылды) .
Мысал келтірейік,
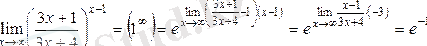 .
.
Ескерту . Егер логарифмдердің негізін e деп алсақ, мұндай логарифмдер натуралдықлогарифмдер, не неперлік логарифмдер делінеді. Непер (1550-1617) - логарифм кестелерін алғашқы жасаушылардың бірі.
Егер х=e y болса, y-ті х санының натуралдық логарифмі дейді, y=lnx деп жазады (y=log e x деудің орнына) .
Бір санның ондық логарифмі мен натуралдық логарифмдерінің байланысын былай табады.
Егер y=lgx, не х=10
y
болса, оны
е
негізінде логарифмдесек ln
x=y×
ln10
,
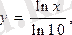
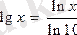 .
.
Егер
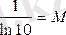 десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
Осылайша, егер санның натуралдық логарифмі белгілі болса, онда оның ондық логарифмін ауысу модуліне көбейту арқылы табады.
ІІ. Шегі бар тізбектердің қасиеттері.
2. 1. Шенелген және шенелмеген тізбектер.
х n (n=1, 2, …) сандарынан тұратын сандар жиынын {хn} тізбегінің мәндерінің жиыны деп атайды.
Мәндерінің жиыны жоғарыдан шенелген болатын, яғни белгілі бір С нақты саны және барлық нөмерлері үшін хn ≤ C теңсіздігі орындалатын {хn} тізбегін жоғарыдан шенелген деп аталады.
Дәл осылайша төменгі жағынан шенелгендік анықталады: белгілі бір С нақты саны және кез келген n оң бүтін сандары үшін хn ≥ C теңсіздігі орындалалуы керек.
Жоғарыдан да, төменнен де шенелген тізбекті шенелген тізбектер деп атайды.
Тізбектерге тән екі қасиеттің шенелгендігі мен шегі бар болуының арасындағы кейбір байланыстарды көрсетейік.
1 0 . Кез келген шенелген тізбектің, әлде ешқандай шегі болмайды, ал шегі бар болса, онда ол тек қана ақырлы болады.
2 0 . Егер {х n } тізбегінің ақырлы шегі болса, онда ол шенелген тізбек болады.
3 0 . Ақырсыз шегі бар тізбек шенелмеген тізбек деп аталады. 10 Егер тізбектің шегі + ∞ немесе − ∞ болса, онда ол сәйкес жоғарыдан және төменнен шенелмеген болады.
4 0 . Егер { х n } ∞ n=1 тізбегі қандай түрде шенелмеген болса (жоғарыдан, төменнен, екі жақты), әрбір т > 1 үшін { х n } ∞ n =m тізбегі де сондай түрде шенелмеген болады.
Мысалдар:
1. х n = жинақталатын (шегі 0 саны), шенелген (себебі x n < 1), мәндерінің жиыны{1, , . . . } ақырсыз жиын болатын тізбек.
2. Тізбек х n = (− 2 ) n ∞-ке ұмтылады, жоғарыдан да, төменнен де шенелмеген: мәндерінің жиыны ақырсыз.
3. х n =n 2 тізбегі + ∞ -ке ұмтылады (сондықтан жоғарыдан шектелмеген), төменнен шенелген (себебі х n ≥ 1), оның мәндерінің жиыны ақырсыз болады.
4. х n = + тізбегінің шегі болмайды, бірақ шенелген оның мәндерінің жиыны ақырлы болады (0 және 1) .
5. х n =1 тізбегінің шегі болады, шенелген, мәндер жиыны ақырлы болады.
6. x n = , тізбегінің шегі болмайды, жоғары жағынан шектелмеген, ал төменнен шенелген, мәндерінің жиыны ақырсыз.
7. 1, n=3k
x n = n, n=3k+1 (k=1, 2…. )
-n, n=3k+2
тізбегінің шегі болмайды, екі жағынан да шенелмеген, мәндерінің жиыны ақырсыз.
2. 2. Жиынтықты тізбектер және олардың негізгі қасиеттері
Монотонды тізбектер саны. е- саны.
e саны.
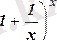 функциясының
функциясының
 шегі
шегі
Жалпы мүшесі
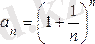 түрінде берілген сан тізбегінің шегін
e
саны деп атайды, яғни
түрінде берілген сан тізбегінің шегін
e
саны деп атайды, яғни
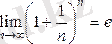 .
e-саны иррационал сан және оның жуық мәнімынадай e =2. 71828128 . . .
.
e-саны иррационал сан және оның жуық мәнімынадай e =2. 71828128 . . .
Теорема
.
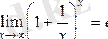 . (**)
. (**)
(**) -формуласын 2-ші тамаша шек деп атайды.
Егерде (**) формулада
 десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:
десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:
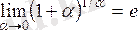 . e-cанын пайдаланып шығарылатын кейбір шектерді келтірейік:
. e-cанын пайдаланып шығарылатын кейбір шектерді келтірейік:
1)
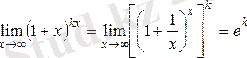 .
.
2)
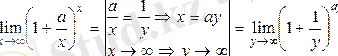 e
e
 .
.
3)
 .
.
3')
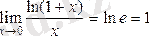 .
.
4)
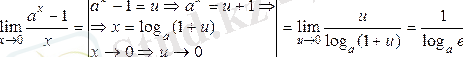
5)

6)
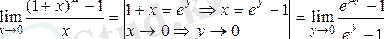
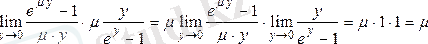
Егерде
 шегін
шегін
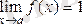 және
және
 болған жағдайда есептеп шығару керек болса, онда
болған жағдайда есептеп шығару керек болса, онда
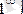 түріндегі анықталмағандық алар едік.
түріндегі анықталмағандық алар едік.
Бұл секілді анықталмағандықтарды ашу үшін, берілген функцияның
 негізі мен дәреже көрсеткішін мына формуланы
негізі мен дәреже көрсеткішін мына формуланы
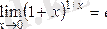 қолдану мүмкін болатындай етіп түрлендіру керек .
қолдану мүмкін болатындай етіп түрлендіру керек .
Мысалы.
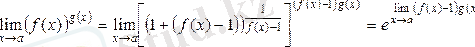 .
.
Осыдан,
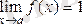 ,
,
 жағдайда, мына формула табылады
жағдайда, мына формула табылады
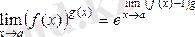 (бұл жерде үзіліссіз ) .
(бұл жерде үзіліссіз ) .
Мысал келтірейік,
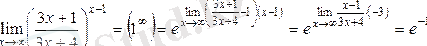 .
.
Ескерту. Егер логарифмдердің негізін e деп алсақ, мұндай логарифмдер натуралдықлогарифмдер, не неперлік логарифмдер делінеді. Непер (1550-1617) - логарифм кестелерін алғашқы жасаушылардың бірі.
Егер х=e y болса, y-ті х санының натуралдық логарифмі дейді, y=lnx деп жазады (y=log e x деудің орнына) .
Бір санның ондық логарифмі мен натуралдық логарифмдерінің байланысын былай табады.
Егер y=lgx, не х=10
y
болса, оны
е
негізінде логарифмдесек ln
x=y×
ln10
,
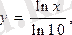
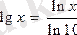 .
.
Егер
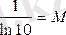 десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
Осылайша, егер санның натуралдық логарифмі белгілі болса, онда оның ондық логарифмін ауысу модуліне көбейту арқылы табады.
2. 3. Функцияның шегі.
Анықтама.
 функциясы
функциясы
 нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін dоң саны табылып, x -тің
нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін dоң саны табылып, x -тің
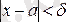 теңсіздігін қанағаттандыратын барлық мәндеріүшін, мына
теңсіздігін қанағаттандыратын барлық мәндеріүшін, мына
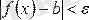 теңсіздік орындалса,
теңсіздік орындалса,
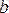 шамасы
шамасы
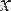 -тің
-тің
 -ға ұмтылғандағы
-ға ұмтылғандағы
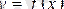 функциясының (
функциясының (
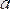 нүктесіндегі ) шегі деп аталады.
нүктесіндегі ) шегі деп аталады.
Осы анықтамадағы
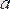 шамасының функцияның анықталу облысына кіруішарт емес, бірақ
шамасының функцияның анықталу облысына кіруішарт емес, бірақ
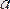 -ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруішарт.
-ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруішарт.
Егер
 шамасы
шамасы
 -ға ұмтылғанда,
-ға ұмтылғанда,
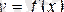 функциясының мәні
функциясының мәні
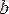 -ға ұмтылса, оны былайша жазатын боламыз
-ға ұмтылса, оны былайша жазатын боламыз
 .
.
Анықтамадағы
 және
және
 шамалары сан болуы да, не ±¥ болуы да мүмкін.
шамалары сан болуы да, не ±¥ болуы да мүмкін.
Егер
 -ның шамасы
-ның шамасы
 символдарының бірі болса,
символдарының бірі болса,
 - шексіз үлкен деп аталады, мұны былай жазамыз
- шексіз үлкен деп аталады, мұны былай жазамыз
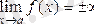 .
.
Егер әрбір e>0 үшін
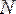 саны табылып,
саны табылып,
 үлкен болғанда
үлкен болғанда
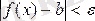 теңсіздігі орындалса,
теңсіздігі орындалса,
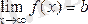 деп жазамыз.
деп жазамыз.
Егер
 -ның шамасы
-ның шамасы
 символдарының бірі болса,
символдарының бірі болса,
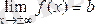 деп жазамыз.
деп жазамыз.
Ендіфункцияның шегінің геометриялық мағынасын анықтайық. Айталық
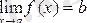 делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
 теңсіздіктерін қанағаттандыратын барлық
теңсіздіктерін қанағаттандыратын барлық
 үшін
үшін
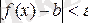 теңсіздігі орындалады деген сөз.
теңсіздігі орындалады деген сөз.
Басқаша айтқанда: аргумент
x
-тің
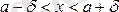 теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
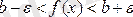 теңсіздігін қанағаттандыруы тиіс.
b
-саны
теңсіздігін қанағаттандыруы тиіс.
b
-саны
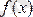 функциясының
х
шамасы
функциясының
х
шамасы
 -ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.
-ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.

 түзулер шектеген алап қандай болса да,
түзулер шектеген алап қандай болса да,
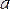 нүктесінің төңірегіне
нүктесінің төңірегіне
 маңайын салуға болады (яғни d>0 саны табылады) . Олай болса, абсциссалары
маңайын салуға болады (яғни d>0 саны табылады) . Олай болса, абсциссалары
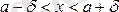
 қисығының барлық нүктелері
қисығының барлық нүктелері
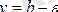 ,
,
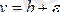 түзулері шектеде жатады (тек абсциссасы
түзулері шектеде жатады (тек абсциссасы
 -ға тең нүкте ғана алапқа енбей қалуы мүмкін) . Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
-ға тең нүкте ғана алапқа енбей қалуы мүмкін) . Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
1)
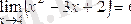 болатынын көрсету керек.
болатынын көрсету керек.
Алдын ала e>0 саны берілсін. Оған сәйкес
 -тің
-тің
 (*)
(*)
теңсіздігін қанағаттандыратын барлық мәндері үшін
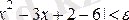 (**)
(**)
теңсіздігі, яғни
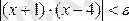 теңсіздігі орындалатын d>0 санын табайық. Ал (*) -дан
теңсіздігі орындалатын d>0 санын табайық. Ал (*) -дан
 теңсіздігі шығады. Демек,
теңсіздігі шығады. Демек,
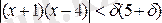 . (***)
. (***)
(**) мен (***) -дан мына қорытындыға келеміз: егер d санын d(5+d) =e тендігін қанағаттандыратын етіп алсақ, (*) (***) да орындалады.
Сонымен,
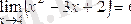 екендігі дәлелденеді.
екендігі дәлелденеді.
2)
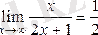 екендігін дәлелдеу керек.
екендігін дәлелдеу керек.
Алдын ала e>0 cаны берілген делік. Сонда аргумент
 теңсіздігін қанағаттандырысымен
теңсіздігін қанағаттандырысымен
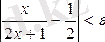 N
санын іздеуіміз керек.
N
санын іздеуіміз керек.
Ал,
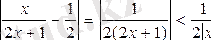 . Cондықтан
. Cондықтан
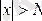 болғанда
болғанда
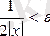 теңсіздігі орындалады. Бұдан
теңсіздігі орындалады. Бұдан
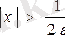 . Демек, егер
. Демек, егер
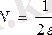 деп алсақ,
деп алсақ,
 болғанда
болғанда
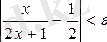 , яғни
, яғни
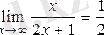 болатыны айқын.
болатыны айқын.
Ескерту. Егер
 функциясы
функциясы
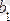 шамасына ұмтылғанда,
x
-тің
шамасына ұмтылғанда,
x
-тің
 -ға ұмтылуы тек
-ға ұмтылуы тек
 -дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
-дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
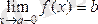 ,
,
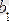 ді функцияның
ді функцияның
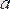 нүктесіндегі сол жақты шегі дейді.
нүктесіндегі сол жақты шегі дейді.
Егер
х
тек
 -дан үлкен мәндер қабылдайтын болса, былай жазып
-дан үлкен мәндер қабылдайтын болса, былай жазып
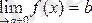 ,
,
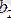 -ні функцияның
-ні функцияның
 нүктесіндегі оң жақты шегі дейді.
нүктесіндегі оң жақты шегі дейді.
Ескерту. Егер аргумент
х
-тің берілген анықталу облысындағы барлық мәндері үшін
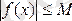 М саны табылса,
М саны табылса,
 функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
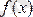 берілген облыста шектелмеген делінеді.
берілген облыста шектелмеген делінеді.
Функцияның шегі
Анықтама.
 функциясы
функциясы
 нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін d оң саны табылып, x -тің
нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін d оң саны табылып, x -тің
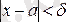 теңсіздігін қанағаттандыратын барлық мәндері үшін, мына
теңсіздігін қанағаттандыратын барлық мәндері үшін, мына
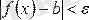 теңсіздік орындалса,
теңсіздік орындалса,
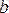 шамасы
шамасы
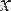 -тің
-тің
 -ға ұмтылғандағы
-ға ұмтылғандағы
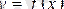 функциясының (
функциясының (
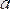 нүктесіндегі ) шегі деп аталады.
нүктесіндегі ) шегі деп аталады.
Осы анықтамадағы
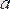 шамасының функцияның анықталу облысына кіруі шарт емес, бірақ
шамасының функцияның анықталу облысына кіруі шарт емес, бірақ
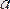 -ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруі шарт.
-ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруі шарт.
Егер
 шамасы
шамасы
 -ға ұмтылғанда,
-ға ұмтылғанда,
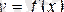 функциясының мәні
функциясының мәні
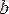 -ға ұмтылса, оны былайша жазатын боламыз
-ға ұмтылса, оны былайша жазатын боламыз
 .
.
Анықтамадағы
 және
және
 шамалары сан болуы да, не ±¥ болуы да мүмкін.
шамалары сан болуы да, не ±¥ болуы да мүмкін.
Егер
 -ның шамасы
-ның шамасы
 символдарының бірі болса,
символдарының бірі болса,
 - шексіз үлкен деп аталады, мұны былай жазамыз
- шексіз үлкен деп аталады, мұны былай жазамыз
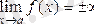 .
.
Егер әрбір e>0 үшін
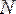 саны табылып,
саны табылып,
 үлкен болғанда
үлкен болғанда
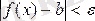 теңсіздігі орындалса,
теңсіздігі орындалса,
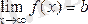 деп жазамыз.
деп жазамыз.
Егер
 -ның шамасы
-ның шамасы
 символдарының бірі болса,
символдарының бірі болса,
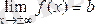 деп жазамыз.
деп жазамыз.
Ендіфункцияның шегінің геометриялық мағынасын анықтайық. Айталық
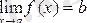 делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
 теңсіздіктерін қанағаттандыратын барлық
теңсіздіктерін қанағаттандыратын барлық
 үшін
үшін
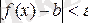 теңсіздігі орындалады деген сөз.
теңсіздігі орындалады деген сөз.
Басқаша айтқанда: аргумент
x
-тің
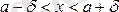 теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
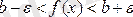 теңсіздігін қанағаттандыруы тиіс.
b
-саны
теңсіздігін қанағаттандыруы тиіс.
b
-саны
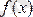 функциясының
х
шамасы
функциясының
х
шамасы
 -ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.
-ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.

 түзулер шектеген алап қандай болса да,
түзулер шектеген алап қандай болса да,
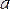 нүктесінің төңірегіне
нүктесінің төңірегіне
 маңайын салуға болады (яғни d>0 саны табылады) . Олай болса, абсциссалары
маңайын салуға болады (яғни d>0 саны табылады) . Олай болса, абсциссалары
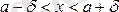 теңсіздіктерін қанағаттандыратын
теңсіздіктерін қанағаттандыратын
 қисығының барлықнүктелері
қисығының барлықнүктелері
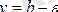 ,
,
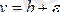 түзулері шектеген алаптың ішінде жатады (тек абсциссасы
түзулері шектеген алаптың ішінде жатады (тек абсциссасы
 -ға тең нүкте ғана алапқа енбей қалуы мүмкін) . Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
-ға тең нүкте ғана алапқа енбей қалуы мүмкін) . Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
1)
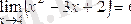 болатынын көрсету керек.
болатынын көрсету керек.
Алдын ала e>0 саны берілсін. Оған сәйкес
 -тің
-тің
 (*)
(*)
теңсіздігін қанағаттандыратын барлық мәндері үшін
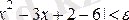 (**)
(**)
теңсіздігі, яғни
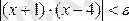 теңсіздігі орындалатын d>0 санын табайық. Ал (*) -дан
теңсіздігі орындалатын d>0 санын табайық. Ал (*) -дан
 теңсіздігі шығады. Демек,
теңсіздігі шығады. Демек,
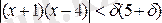 . (***)
. (***)
(**) мен (***) -дан мына қорытындыға келеміз: егер d санын d(5+d) =e тендігін қанағаттандыратын етіп алсақ, (*) (***) да орындалады.
Сонымен,
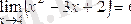 екендігі дәлелденеді.
екендігі дәлелденеді.
2)
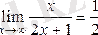 екендігін дәлелдеу керек.
екендігін дәлелдеу керек.
Алдын ала e>0 cаны берілген делік. Сонда аргумент
 теңсіздігін қанағаттандырысымен
теңсіздігін қанағаттандырысымен
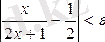 N
санын іздеуіміз керек.
N
санын іздеуіміз керек.
Ал,
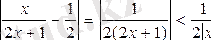 . Cондықтан
. Cондықтан
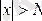 болғанда
болғанда
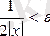 теңсіздігі орындалады. Бұдан
теңсіздігі орындалады. Бұдан
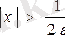 . Демек, егер
. Демек, егер
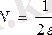 деп алсақ,
деп алсақ,
 болғанда
болғанда
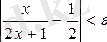 теңсіздігі орындалатыны, яғни
теңсіздігі орындалатыны, яғни
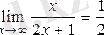 болатыны айқын.
болатыны айқын.
Ескерту. Егер
 функциясы
функциясы
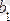 шамасына ұмтылғанда,
x
-тің
шамасына ұмтылғанда,
x
-тің
 -ға ұмтылуы тек
-ға ұмтылуы тек
 -дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
-дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
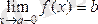 ,
,
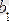 ді функцияның
ді функцияның
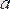 нүктесіндегі сол жақты шегі дейді.
нүктесіндегі сол жақты шегі дейді.
Егер
х
тек
 -дан үлкен мәндер қабылдайтын болса, былай жазып
-дан үлкен мәндер қабылдайтын болса, былай жазып
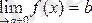 ,
,
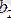 -ні функцияның
-ні функцияның
 нүктесіндегі оң жақты шегі дейді.
нүктесіндегі оң жақты шегі дейді.
Ескерту. Егер аргумент
х
-тің берілген анықталу облысындағы барлық мәндері үшін
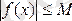 М саны табылса,
М саны табылса,
 функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
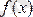 берілген облыста шектелмеген делінеді.
берілген облыста шектелмеген делінеді.
Шексіз аз шама және оның қасиеттері
Анықтама. Егер
 не
не
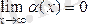 болса,
болса,
 функциясы
функциясы
 не
x
®¥ болғанда шексіз аз шама делінеді.
не
x
®¥ болғанда шексіз аз шама делінеді.
Шектің анықтамасына сүйеніп, жоғарыдағы анықтаманы былайша тұжырымдауға болады: алдынала берілген кез-келген жеткілікті аз e>0 саны үшін
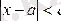 теңсіздігі орындалатын
x -
тың мәндері үшін
теңсіздігі орындалатын
x -
тың мәндері үшін
 теңсіздігі орындалатындай d саны табылса, a(x) шексіз аз шама делінеді (x®
теңсіздігі орындалатындай d саны табылса, a(x) шексіз аз шама делінеді (x®
 ) .
) .
Мысалы.
1) функция a(x) =(x-2)
2
, x шамасы 2-ге ұмтылғанда шексіз аз шама, өйткені
 .
.
2) функция a(x) =
 , х®¥ болғанда шексіз аз шама, өйткені
, х®¥ болғанда шексіз аз шама, өйткені
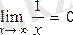 .
.
Теорема. Егер
 функциясы
b
санымен шексіз аз шама a-нің қосындысына тең болса, яғни y=b+a болса, lіm y=b (x®a не х®¥) болады. Керісінше, егер
функциясы
b
санымен шексіз аз шама a-нің қосындысына тең болса, яғни y=b+a болса, lіm y=b (x®a не х®¥) болады. Керісінше, егер
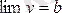 болса,
болса,
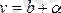 деп жазуға болады. Мұндағы a шексіз аз шама.
деп жазуға болады. Мұндағы a шексіз аз шама.
Теорема. Егер
 шамасы
шамасы
 -ға ұмтылғанда a(x) нольге ұмтылса, y=
-ға ұмтылғанда a(x) нольге ұмтылса, y=
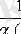 шексіз үлкен шамаға ұмтылады.
шексіз үлкен шамаға ұмтылады.
Теорема. Бірнеше (саны шектеулі) шексіз аз шамалардың алгебралық қосындысы шексіз аз шама болады.
Теорема. Шексіз аз шама a(x) -тың шектелген g(x) функциясына көбейтіндісі (x®
 , x®¥) шексіз аз шама.
, x®¥) шексіз аз шама.
Салдар. Егер lіm a(x) =0, lіm b(x) =0 болса, lіmab=0.
Салдар. Егер lіm a(x) =0, c=const болса, lіm ca=0.
Теорема. Егер lіma(x) =0, lіmb(x) ¹0 болса a(x) ·b -1 (x) -шексіз аз шама болады.
Шектер туралы негізгі теоремалар
Теорема. Бірнеше (саны шектеулі) функциялардың қосындысының шегі сол функциялардың шектерінің қосындысына тең
lіm(u 1 +u 2 + . . . +u k ) = lіm u 1 +lіm u 2 + . . . +lіm u k .
Теорема. Бірнеше (саны шектеулі) айнымалы шегі сол шамалардың тең:
lіm(u 1 u 2 . . . u k ) =lіm u 1 lіm u 2 . . . lіm u k .
Теорема.

 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz