Көпбұрыш

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

Тақырыптар:

Көпбұрыш.

Үшбұрыш оның қасиеттері.

Үшбұрыштың медианасы, биссектриясы, биіктігі, орта сызығы, тең бүйірлі, тең қабырғалы, тік бұрышты үшбұрыш.

Төртбұрыштар.

Параллелограм.

Ромб.

Тік төртбұрыштар

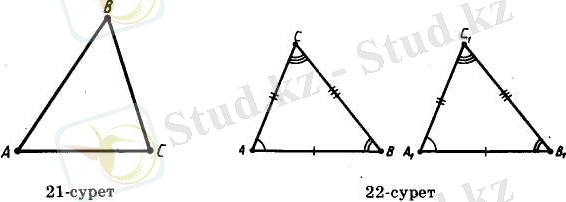
ҰШБҰРЫШ

Үшбұрыш деп бір түзуде жатпайтын үш нүктеден және осы нүктелерді қос-қостан қосатын үш кесіндіден тұратын фигураны атайды. Нүктелер үшбұрыштың төбелері, ал кесінділер қабырғалары деп аталады.

21-суретте төбелері А, В, С, ал қабырғалары АВ, ВС, AC болатын үшбұрыш кескінделген. Ұшбұрышты төбелері арқылы белгілейді. «Үшбұрыш» деген сөздің орнына кейде Д таңбасын қолданады. Мысалы, 21-суреттегі үшбұрыш былай белгіленеді: ABC.

ABC үшбұрышының A төбесіндегі бұрышы деп АВ және AC жарты түзулерімен жасалатын бұрышты айтады. Үшбұрыштың В және С төбелеріндегі бұрыштары да осылай анықталады.

Егер екі кесіндінің ұзындықтары бірдей болса, онда олар тең кесінділер деп аталады. Егер екі бұрыштың градус есебімен бұрыштың шамалары бірдей болса, онда олар тең бұрыштар деп аталады.

Егер екі кесіндінің ұзындықтары бірдей болса, онда олар тең кесінділер деп аталады. Егер екі бұрыштың градус есебімен бұрыштық шамалары бірдей болса, онда олар тең бұрыштер деп аталады.

Егер үшбұрыштардың сәйкес қабырғалары және сәйкес бұрыштары тең болса, онда олар тең ұшбұрыштар деп аталады. Сонда сәйкес бұрыштар сәйкес қабырғаларға қарсы жатуы тиіс.

22-суретте өзара тев АВС және А ₁ В ₁ С ₁ ұшбұрыштары көрсетілген.

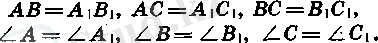
Сызбада тең кесінділерді, әдетте бір, екі не үш сызықшамен, ал тең бұрыштарды бір, екі не үш кішкене доғамен белгілейді.

Үшбұрыштардың теңдігін көрсету үшін, әдетте теңдік белгісі «=» пайдаланылады. АВС = А ₁ В ₁ С ₁ жазуы былай оқылады: «ABC үшбұрышы Д5, С, үшбұрышына тең». Бұл жерде үшбұрыш төбелерінің жазылу ретінің мәні бар. АВС = і А ₁ В ₁ С ₁ теңдігі мынаны білдіреді:< A = < A _l < B = < B ₂ . . . Ал, АВС = В ₁ А ₁ С ₁ . теңдігінің мәнісі мүлде басқаша: < A = < B ₁ , < B = < A _1,

БЕРІЛГЕН ҮШБҰРЫШҚА ТЕҢ ҮШБҰРЫШТЫҢ БОЛАТЫНЫ ТУРАЛЫ

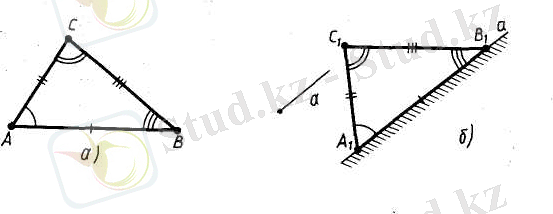
Айталық, бізде ABC үшбұрышы және а сәулесі бар болсын (23, а-сурет) . ABC үшбұрышын басқаша орналастырайық: оның А төбесі а сәулесінің бас нүктесімен беттессін, В төбесі а сәулесінде жатсын, ал С төбесі а сәулесі мен оның жалғасына қатысты берілген жарты жазықтықта жатсын. Орны өзгерген

23-сурет

үшбұрыштың осы жаңа қалыптағы төбелерін А ₁ , В ₁ , С ₁ деп белгілейік (23, б-сурет) .

А ₁ , В ₁ , С ₁ үшбұрышы ABC үшбұрышына тең.

ABC үшбұрышына тең және берілген а сәулесіне қатысты көрсетілген қалыпта орналасқан А ₁ , В ₁ , С ₁ үшбұрышының бар болуын біз қарапайым фигуралардың негізгі қасиеттерінің қатарына жатқызамыз. Бұл қасиетті былай тұжырымдаймыз:

VIII. Үшбұрыш қандай болса да, берілген жарты түзуге қатысты көрсетілген қалыпта орналасқан оған тең үшбұрыш бар болады.

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ БЕЛГІЛЕРІ

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ БІРІНШІ БЕЛГІСІ

Теорема 3. 1 (екі қабырғасы және олардың арасындағы бұрышы бойынша үшбұрыштардың теңдік белгісі) . Егер бір үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы сәйкесінше екінші үшбұрыштың екіқабырғасы мен олардың арасындағы бұрышына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелдеу. Айталық, ABC және А ₁ , В ₁ , С ₁ үшбұрыштарында <A= А ₁ , АВ = АВ ₁ , АС = А ₁ С болсын (44-сурет) . Үшбұрыштар тең болатынын дәлелдейміз.

Айталық, А ₁ , В ₂ , С ₂ - ABC үшбұрышына тең үшбұрыш болсын, оның В ₁ төбесі А ₁ , В ₁ сәулесінде жатсын, С ₂ төбесі С ₁ төбесімен бір жарты жазықтықта жатсын (45, а-сурет) .

А ₁ В ₁ =А ₁ В ₂ болатындықтан, В ₂ төбесі В ₂ төбесімен беттеседі (45, а-сурет) . <В ₁ , A ₁ С ₁ = <В ₁ , A ₁ С ₁ болғандықтан, А ₁ С ₂ сәулесі A ₁ С ₁ сәулесімен беттеседі (45, в-сурет) . A ₁ С ₁ = A ₁ С ₂ болғандықтан, С ₂ төбесі С ₁ төбесімен беттеседі (45, г-сурет) .

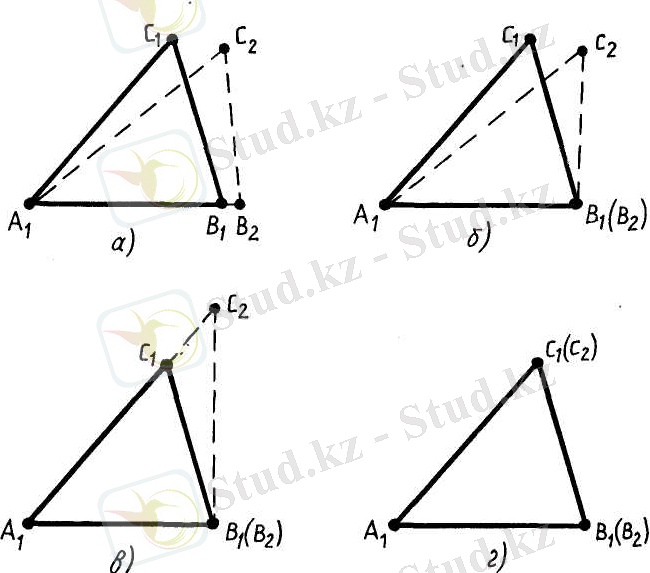
45-сурет

Сонымен, <В ₁ , A ₁ С ₁ үшбұрышы А ₁ В ₂ С ₂ үшбұрышымен беттеседі, демек ABC үшбұрышына тең болады. Теорема дәлелденді.

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ ЕКІНШІ БЕЛГІСІ

Теорема 3. 2 (бір қабырғасы және оған іргелес бұрыштары бойынша үшбұрыштардың теңдік белгісі) . Егер бір үш-бұрыштың бір қабырғасы мен оған іргелес бұрыштары сәйкесінше екінші үшбұрыштың бір қабырғасы мен оған іргелес бұрыштарына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелдеу. Айталық, ABC және В ₁ , A ₁ С ₁ -екі үшбұрыш, оларда АВ = AВ = А ₁ және <A=<A ₁ және <В=<В ₁ болсын (47-сурет) . Үшбұрыштардың тең екенін дәлелдейік.

Айталық, A ₁ В ₂ С ₂ - ABC үшбұрышына тең үшбұрыш болсын, төбесі-А ₁ В ₁ сәулесінде жатсын, ал С ₂ төбесі С ₁ төбесімен түзуіне қарағанда бір жарты жазықтықта жатсын.

\В ₂ = А\В\ болғандықтан, В ₂ төбесі В\ төбесімен беттеседі. А\Сч= /LB\AiC\ және /-А\В\С ₂ = /-А\В\С\ болғандықтан,

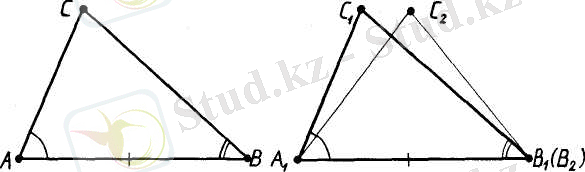
47-сурет

А ₁ С ₂ сәулесі А ₁ С ₁ сәулесімен беттеседі, ал В ₁ С ₂ сэулесі В ₁ С ₁ сәулесімен беттеседі. Б9дан С ₁ төбесі С ₂ төбесімен беттесетіндігі шығады.

Сонымен, А ₁ В ₁ С ₁ үшбүрышы А ₁ В ₂ С ₂ үшбұрышымен беттеседі, демек, ABC үшбұрышына тең болады. Теорема дәлелденді.

ҮШБҰРЫШТЫҢ БИІКТІГІ, БИССЕКТРИСАСЫ ЖӘНЕ МЕДИАНАСЫ

Үшбұрыштың берілген төбесінен түсірілген биіктігі деп осы төбеден үшбұрыштың қарсы жатқан қабырғасын қамтитын түзуге жүргізілген перпендикулярды айтады.

олардың В және В ₁ төбелерінен биіктіктер жүргізілген. 51, а-суретте биіктіктің табаны үшбұрыштың қабырғасында жатыр, ал 51, б-суретте үшбұрыш қабырғасының созындысында жатыр.

Үшбұрыштың берілген төбесінен жүргізілген биссектрисасы деп үшбұрыш бұрышының биссектрисасының осы төбені қарсы жатқан қабырғадағы нүктемен қосатын кесіндісін айтады (52, а-сурет) .

Үшбұрыштың берілген төбесінен жүргізілген медианасы деп осы төбені қарсы жатқан қабырғаның ортасымен қосатын кесіндіні айтады (52, б-сурет) .

ҮШБҰРЫШТАР ТЕҢДІГІНІҢ ҮШІНШІ БЕЛГІСІ

Теорема 3. 6 (үшбұрыштардың үш қабырғасы бойынша теңдік белгісі) . Егер бір үшбұрыштың үш қабырғасы сәйкесінше екінші үшбұрыштың үш қабырғасына тең болса, онда мұндай үшбұрыштар тең болады.

Дәлелдеу. Айталық, ABC және А ₁ В ₁ С ₁ үшбұрыштарында АВ = А ₁ В ₁ , AC = A ₁ С ₁ , ВС = В ₁ С ₁ болсын (55-сурет) . Үшбұрыштар тең екенін дәлелдеу керек.

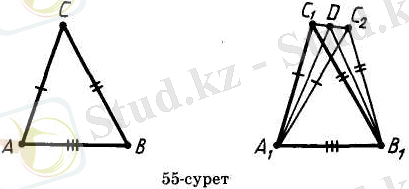
Үшбұрыштар тең емес деп жориық. Сонда <A < А ₁ , <В <В _1, <C C ₁ , болсын. Әйтпесе, олар бірінші белгі бойынша тең болар еді.

Айталық, А ₁ В ₁ С ₁ -ABC үшбұрышына теқ үшбұрыш болсын: оның С ₂ төбесі С ₁ төбесімен А ₁ В ₁ түзуіне қатысты бір жарты жазықтықта жатсын (55-суретті қараңдар) .

D нүктесі - С ₁ С ₂ кесіндісінің ортасы болсын. Сонда А ₁ С ₁ С ₂ және В ₁ С ₁ С ₂ - үшбұрыштары тең бүйірлі, ал С ₁ С ₂ бұларға ортақ табан болады. Сондықтан бұлардың A ₁ D және B ₁ D медианалары биіктіктер де болып табылады. Демек, A ₁ D және B ₁ D түзулері С ₁ С ₂ түзуіне перпендикуляр болады. A ₁ D және B ₁ D түзулері беттеспейді, өйткені А ₁ , В ₁ . D нүктелері бір түзуде жатпайды. Ал С ₁ С ₂ түзуінің D нүктесі арңылы оған тек қана бір перпендикуляр түзу жүргізуге болады. Біз қайшылыққа келдік. Теорема дәлелденді.

56-сурет

ҮШБҰРЫШТЫҢ БҰРЫШТАРЫНЫҢ ҚОСЫНДЫСЫ

Т е о р е м a 4. 4 Үшбұрыштың бұрыштарының қосындысы 180°-қа тең.

Дәлелдеу. ABC берілген үшбұрыш болсын. В төбесі арқылы AC түзуіне параллель түзу жүргіземіз. А және D нүктелері ВС түзуінің әр жағында жататындай етіп D нүктесін белгілейміз (78-сурет) .

DBC және АСВ бұрыштары - ішкі айқыш бұрыштар. Сондықтан олар тең. Олай болса, үшбұрыштың В және С төбелеріндегі бұрыштарының қосындысы ABD бұрышына тең.

Сонда үшбұрыштың барлық үш бұрышының қосындысы ABD және ВАС бұрыштарының қосындысына тең. Ал бұлар AC жөне BD параллель түзулері мен АВ қиюшысы жасайтын ішкі тұстас бұрыштар, сондықтан бұлардың қосындысы 180°-қа тең. Теорема дәлелденді.

4. 4-теоремадан мынадай салдар шығады: кез келген үшбұрыштың ең кемінде екі бұрышы сүйір болады.

Шынында да, үшбұрыштың тек қана бір бұрышы сүйір немесе оның сүйір бұрышы мүлдем жоқ деп ұйғарсақ, сонда бұл үшбұрыштың әрбіреуі 90°-таи кем емес екі бұрышы бар болады. Осы екі бұрыштың қосындысы-ақ, 180°-тан кем емес болады. Ал, бұл мүмкін емес, өйткені үшбұрыштың барлық бұрыштарының қосындысы 180°-қа тең. Дәлелдеу керегі де осы еді.

ҮШБҰРЫШТЫҢ СЫРТҚЫ БҰРЫШТАРЫ

Үшбұрыштын берілген төбесіндегі сыртқы бұрышы деп осы төбедегі үшбұрыштын бұрышымен сыбайлас бұрышты атайды (79-сурет) .

Берілген төбедегі үшбұрыштың бұрышын осы төбедегі оның сыртқы бұрышымен шатастырмас үшін оны кейде ішкі бұрыш деп атайды.

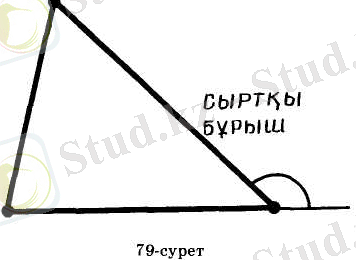
Т е о р е м a 4. 5. Үшбұрыштың сыртқы бұрышы онымен сыбайлас емес екі ішкі бұрыштың қосындысына тең болады.

Дәлелдеу. ABC - берілген үшбұрыш болсын (80-сурет) . Үшбұрыштың бұрыштарының қосындысы туралы теорема бойынша

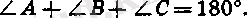
Бұдан

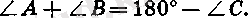
Бұл теңдіктің оң жақ бөлігінде үшбұрыштың С төбесіндегі
сыртқы бұрыштың градустық өлшемі тұр. Теорема дәлелденді.
4. 5-теоремадан мынадай салдар шығады: үшбұрыштың сыртқы бұрышы онымен сыбайлас емес кез келген ішкі бұрыштан үлкен болады.

ҮШБҰРЫШ ТЕҢСІЗДІГІ

Егер А мен В әр түрлі нүктелер болса, онда олардың ара қашықтығы деп АВ кесіндісінің ұзындығын атайды. Егер A мен В нүктелері дәл келіп беттесетін болса, онда олардың ара қашықтығы нөлге тең деп алынады.

Т е о р е м a 7. 3 (үшбұрыш теңсіздігі) . Үш нүкте қандай болғанмен де, ол үш нүктенің кез келген екеуінің ара қашықтығы олардың үшінші нүктеге дейінгі ара қашықтықтарының қосындысынан артық болмайды.

Ал бұл осы ара қашықтықтардың әрқайсысы да қалған екеуінің қосындысынан кіші не оған тең дегенді білдіреді.

Дәлелдеу. А, В, С - берілген үш нүкте болсын. Егер осы үш нүктенің екеуі немесе тіпті үшеуі де беттесетін болса, онда теорема тұжырымы өзінен-өзі айқын.

Егер үш нүктенің барлығы да әр түрлі нүктелер болып және бір түзудің бойында жатса, олардың біреуі, мысалы В нүктесі, былайғы екеуінің арасында жатады. Бұл жағдайда АВ+ВС = АС. Бұдан байқайтынымыз: ол үш ара қашықтықтың әр-қайсысы былайғы екеуінің қосындысынан артық болмайды.

Енді үш нүкте бір түзуде жатпайды деп ұйғарайық (154-сурет) . Сонда АВ<АС+ВС болатындығын дәлелдейміз. АВ түзуіне CD перпендикулярын түсіреміз. Жоғарыда дәлелдегеніміз бойынша AB AD+BD. Сонымен бірге AD<AC және BD<BC болғандықтан, АВ< AC<BC. Теорема дәлелденді.

Үш нүкте бір түзудің бойында жатпайтын жағдайда үшбұрыш теңсіздігі - қатаң теңсіздік екенін ескертеміз. Мұның мәнісі - кез келген үшбұрыштың әрбір қабырғасы былайғы екі қабырғасының қосындысынан кіші болады.

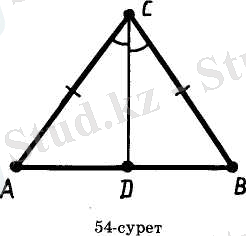
ТЕҢ БҮЙІРЛІ ҮШБҰРЫШТЫҢ МЕДИАНАСЫНЫҢ ҚАСИЕТІ

Т е о р е м a 3. 5 (тең бүйірлі үшбұрыштың медианасының қасиеті) . Тең бүйірлі үшбұрыштың табанына жүргізілген медианасы оның биссектрисасы да, биіктігі де болып табылады.

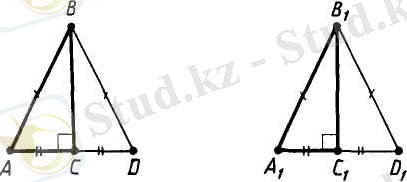
Дәлелдеу. ABC - табаны АВ болатын тең бүйірлі үшбұрыш, ал CD - оның табанына жүргізілген медианасы болсын (53-сурет) .

Үшбұрыштар теңдігінің бірінші белгісі бойынша CAD және CBD үшбұрыштары тең. (Оларда АС=ВС, өйткені ABC үшбұрышы тең бүйірлі. Тең бүйірлі үшбұрыштың табанындағы бұрыштар болғандықтан, < CAD= <CBD. AD және BD қабырғалары тең, өйткені D нүктесі - АВ кесіндісінің ортасы) .

Үшбұрыштардың теңдігінен келесі бұрыштардың теңдігі шығады: < ACD = <BCD, <ADC= < BCD. ACD және BCD бұрыштары тең болғандықтан, CD биссектриса болады. ADC және BDC бұрыштары сыбайлас және тең болғандықтан, олар - тік бұрыштар, сондықтан CD үшбұрыштың биіктігі болады. Теорема дәлелденді.

Үшбұрышқа сырттай сызылған шеңбер

Егер шеңбер үшбұрыштатың барлық төбелері арқылы өтсе, онда ол үшбұрышқа сырттай сызылған шеңбер деп аталады.

Теорема 5. 1. Үшбұрышқа сырттай сызылған шеңбердің

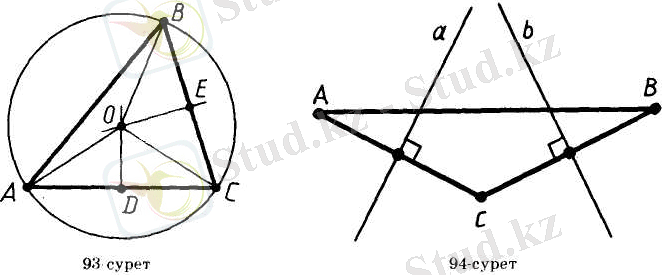
центрі үшбұрыш қабырғаларының орталары арқылы жүргі-зілген перпендикулярдың қиылысу нүктесі болып табылады.

Дәлелдеу. Айталық ABC - берілген үшбұрыш және О - оған сырттай сызылған шеңбердің центрі болсын (93-сурет) . АОС үшбұрышы тең бүйірлі: оның ОА мен ОС қабырғалары радиустар болғандықтан тең. Бұл үшбұрыштың OD медианасы оның биіктігі де болып табылады. Сондықтан шеңбердің центрі AC қабырғасына перпендикуляр әрі оның ортасынан өтетін түзудің бойында жатады. Дәл осылайша шеңбердің центрі үшбұрыштың қалған екі қабырғасының да перпендикулярында жататыны дәлелденеді. Теорема дәлелденді.

ҮШБҰРЫШҚА ІШТЕЙ СЫЗЫЛҒАН ШЕҢБЕР

Егер шеңбер үшбұрыштың барлық қабырғаларын жанайтын болса, онда ол үшбұрышқа іштей сызылған деп аталады.

Теорема. 5. 2. Үшбұрышқа іштей сызылған шеңбердің центрі осы үшбұрыштың биссектрисаларының қиылысу нүктесі болады.

Дәлелдеу. Айталық, ABC - берілген үшбұрыш, О - оған іштей сызылған шеңбердің центрі, D, Е және Ғ шеңбердің қабырғалармен жанасу нүктелері болсын (98-сурет) . Тік бұрышты

үшбұрыштар AOD және АОЕ гипотенузасы мен катеті бойынша тең. Бұлардың АО гипотенузасы ортақ, ал OD және ОЕ катеттері радиустар болғандықтан тең. Үшбұрыштардың теңдігінен OAD және ОАЕ бұрыштарының теңдігі шығады.

Демек, О нүктесі үшбұрыштың А төбесінен жүргізілген бис-сектрисаның бойында жатады. Дәл осылайша, О нүктесі үшбұрыштың қалған екі биссектрисасының да бойында жататыны дәлелденеді. Теорема дәлелденді.

ҮШБҰРЫШТЫҢ АУДАНЫ ҮШІН ГЕРОН ФОРМУЛАСЫ

Есеп (29) . Үшбұрыштың ауданы үшін Герон формуласын қорытып шығарыңдар:

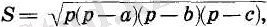
мұндағы a, b, c - үшбұрыш қабырғаларының ұзындықтары, ал - жарты периметр.

Шешеуі. Мынау белгілі:

мұндағы - үшбұрыштың с қабырғасына қарсы жатқан бұрышы. Косинустар теоремасы бойынша

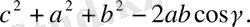
Бұдан

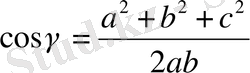
Демек,

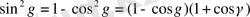
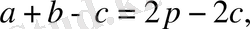
Енді екенін ескеріп, мынаны табамыз:

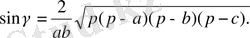
Сонымен

ҮШБҰРЫШТЫҢ ОРТА СЫЗЫҒЫ

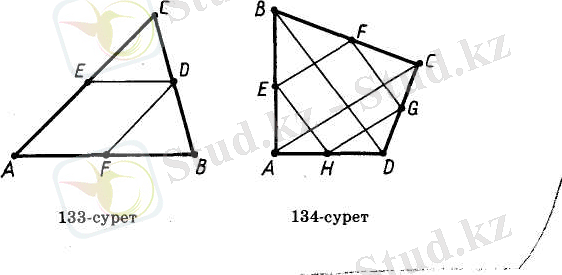
Үшбұрыштың орта сызығы деп оның екі қабырғасының орталарын қосатын кесіндіні атайды.

Теорема 6. 7. Үшбұрыштың берілген екі қабырғасының орталарын қосатын орта сызығы оның үшінші қабырғасына параллель және оның жартысына тең болады.

Дәлелдеу. DE - ABC үшбұрышының орта сызығы болсын (133-сурет) . D нүктесі арқылы АВ-ге параллель түзу жүргіземіз. Бұл түзу Фалес теоремасы бойынша AC кесіндісінің ортасынан өтеді, яғни DE орта сызығын қамтиды. Ендеше, DE орта сызығы АВ қабырғасына параллель.

Енді DF орта сызығын жүргіземіз. Ол AC қабырғасына параллель. AEDF төртбұрышы - параллелограмм. Параллелограмның қасиеті бойынша ED=AF, ал Фалес теоремасы бойынша АҒ=ҒВ. Сондықтан ED= АВ. Теорема дәлелденді.

ТІК БҰРЫШТЫ ҮШБҰРЫШТЫҢ ҚАБЫРҒАЛАРЫ МЕН БҰРЫШТАРЫНЫҢ АРАСЫНДАҒЫ ҚАТЫСТАР

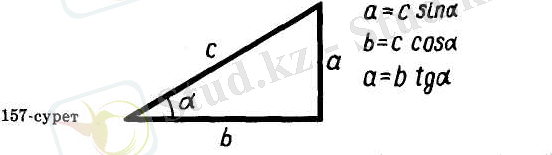
ABC - тік бұрышты үшбұрыш болсын және оның С бұрышы тік те , ал А төбесіндегі сүйір бұрышы а-ға тең болсын (156-сурет) . Анықтама бойынша cos дегеніміз бұрышына іргелес жатқан катеттің гипотенузаға қатынасына тең болады) .

бұрышының синусы деп (белгіленуі sin ) қарсы жаті ВС катеттің гипотенуза АВ-ге қатынасын атайды:

бұрышының тангенсі деп (беягіленуі tg ) қарсы жатқан ВС катеттің іргелес жатқан AC катетке қатынасын атайды.

Бұрыштың синусы мен тангенсі де, косинусы сияқты, тек бұрыштың шамасына ғана тәуелді болады.

Шынында да, Пифагор теоремасы бойынша

Анықтама бойынша

ВС мәнін орнына қоямыз:

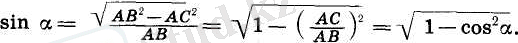
cos мәні тек бұрыштың шамасына ғана тәуелді болатындықтан, sin да тек бұрыштың шамасына ғана тәуелді болады.

Анықтама бойынша

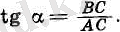
Бөлшектің алымы мен бөлімін АВ-гe бөлейік:

Бұған қарағанда, tg a да тек бұрыштың шамасына ғана тәуелді болады.

sin a, cos a және tg a анықтамаларынан мынадай ережелер шығады:

бұрышына қарсы жатқан катет гипотенуза мен sin -ның көбейтіндісіне тең .

бұрышына іргелес жатқан катет гипотенуза мен cos -ның көбейтіндісіне тец.

бұрышына қарсы жатқан катет екінші катет пен tg а-ның көбейтіндісіне тең.

Осы ережелерді пайдаланып, тік бұрышты үшбұрыштың қабырғаларының бірі мен сүйір бұрышы берілгенде басқа қалған екі қабырғасын табуға болады; екі қабырғасы берілгенде, сүйір бұрыштарын табуға болады (157-сурет) .

ТЕҢ БҮИІРЛІ ҮШБҰРЫШ

Егер үшбұрыштың екі қабырғасы тең болса, ол тең бүйірлі үшбұрыш деп аталады. Бұл тең қабырғалар үшбұрыштың бүйір қабырғалары деп, ал үшінші қабырғасы үшбұрыштың табаны деп аталады.

48-суретте тең бүйірлі ABC үшбұрышы кескінделген. AC мен ВС - оның бүйір қабырғалары, ал АВ - табаны.

Теорема 3. 3 (тең бүйірлі үшбұрыштың бұрыштарының қасиеті) . Тең бүйірлі үшбұрыштың табанындағы бұрыштары тең болады.

Дәлелдеу. Айталың, ABC - табаны АВ болатын тең бүйірлі үшбұрыш болсын (48-сурет) . Ондағы <A = <B екенін дәлелдейміз.

Үшбұрыштардың теңдігінің бірінші белгісі бойынша CAB үшбұрышы СВА үшбұрышына тең. Шынында да, СА = СВ, СВ = СА, АС=АС. Үшбұрыштардың теңдігінен <А=<В екендігі шығады. Теорема дәлелденді.

Барлық қабырғалары тең болатын үшбұрыш тең қабырғалы үшбұрыш деп аталады

ТІК БҰРЫШТЫ ҮШБҰРЫШ

Егер үшбұрыштың тік бұрышы бар болса, ол тік бұрышты үшбұрыш деп аталады. Үшбұрыштың бұрыштарының қосындысы 180°-қа тең болғандықтан, тік бұрышты үшбұрышта тек қана бір тік бұрыш бар болады. Тік бұрышты үшбұрыштың қалған екі бұрышы сүйір болады. Тік бұрышты үшбұрыштын, сүйір бұрыштарының қосындысы 90°-қа тең болады (180°-90 =90 ) .

Тік бұрышты үшбұрыштың тік бұрышына қарсы жатқан қабырғасы гипотенуза деп, қалған екі қабырғасы катеттер деп аталады (82-сурет) .

Тік бұрышты үшбұрыштардың гипотенузасы мен катеті бойынша теңдік белгісін келтіреміз:

Егер бір тік бұрышты үшбұрыштың гипотенузасы мен катеті сәйкесінше екінші үшбұрыштың гипотенузасы мен катетіне тең болса, онда мұндай үшбұрыштар тең болады (83-сурет) .

Бұл белгінің дәлелденуі 3-та 29-есептің шешуі ретінде берілген.

ТІК БҰРЫШТЫ ҮШБҰРЫШТАРДЫҢ ҰҚСАСТЫҒЫ

Тік бұрышты үшбұрыштың бір бұрышы тік. Сондықтан 11. 2-теорема бойынша тік бұрышты үшбұрыштар ұқсас болу үшін олардың бір сүйір бұрыштары тең болуы жеткілікті.

Тік бұрышты үшбұрыштардың осы ұқсастың белгісін пайдалана отырып, үшбұрыштардағы қайсыбір қатыстарды дәлелдейік.

Айталық, ABC - тік бұрышты үшбұрыш та және оның С бұрышы тік болсын. Тік бұрыштың төбесінен CD биіктігін жүргізейік (243-сурет) .

ABC және CBD үшбұрыштарының В төбесіндегі бұрышы ортақ. Олай болса, олар ұқсас болады: ABC CBD . Үшбұрыштардың ұқсастығынан олардың сәйкес қабырғаларының пропорционалдығы шығады:

немесе

Бұл қатынасты әдетте былай тұжырымдап айтады: тік бұрышты үшбұрыштың катеті гипотенуза мен сол катеттің гипотенузаға түсірілген проекциясының арасындағы пропорционал ортасы болады.

Тік бұрышты ACD және CBD үшбұрыштары да ұқсас. Олардың А мен С төбелеріндегі сүйір бұрыштары тең. Бұл үшбұрыштардың ұқсастығынан олардың қабырғаларының пропорционалдығы шығады:

Бұл қатынасты әдетте былай тұжырымдап айтады: тік бұрышты үшбұрыштың тік бұрышының төбееінен жүргізілген биіктігі катеттердің гипотенузаға түсірілген проекцияларының арасындағы орта пропорционалы болады.

Үшбұрыш биссектрисасының келесі қасиетін дәлелдейік:

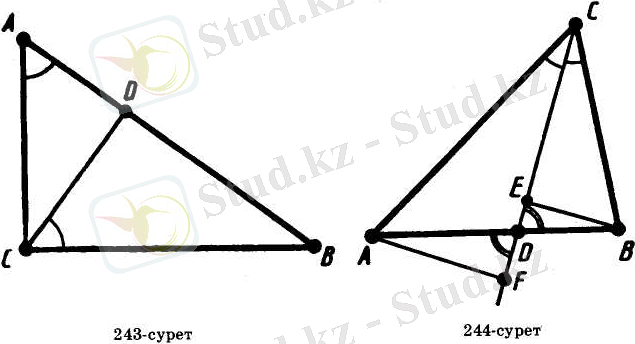
үшбұрыштың биссектрисасы қарсы жатқан қабырғаны былайғы екі қабырғаға пропорционал кесінділерге бөледі.

Айталық, CD - ABC үшбұрышының биссектрисасы болсын (244-сурет) . Егер де ABC үшбұрышы тең бүйірлі болып және де табаны АВ болса, онда әлгі айтылған биссектрисаның қасиеті өз-өзінен айқын, өйткені бұл жағдайда биссектриса әрі медиана болып табылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.