Тұжырымдар алгебрасы, тұжырымдар есептелімі және предикаттық логика негіздері


МАЗМҰНЫ
КІРІСПЕ 3
1 ТАРАУ. ТҰЖЫРЫМДАР АЛГЕБРАСЫ5
1. 1. Тұжырым ұғымы5
1. 2. Тұжырымдарға қолданылатын логикалық амалдар. Терістеу 7
1. 3 Конъюнкция 8
1. 4 Дизъюнкция 9
1. 5 Эквиваленция 10
1. 6 Импликация 11
1. 7 Тұжырымдар алгебрасының формулалары 13
1. 8 Тұжырымдар алгебрасының пара-пар, тепе-тең ақиқат және тепе-тең жалған формулалары 15
2 тарау. тұжырымдар есептелімі166
2. 1 Тұжырымдар есептелімі формуласының ұғымы166
2. 2. Дәлелденетін формула ұғымы188
2. 3 Тұжырымдар есептелімінің аксиомалар жүйесі 19
3 ТАРАУ
3. 1 Предикат ұғымы200
3. 2 Предикаттарға логикалық амалдарды қолдану211
3. 3 Кванторлық амалдар222
3. 4 Предикаттар логикасының формуласының ұғымы233
3. 5 Предикаттар логикасының формулаларының тепе-теңдігі 25
Қорытынды . . . 26
Пайдаланылған әдебиеттер . . . 27
КІРІСПЕМатематика барлық тұжырымдар ақыл қорытындысы арқылы, яғни адамның ойлау қабілеті заңының жолдарын қолданып, дәлелденетін ғылым болып табылады. Адамның ойлау қабілетінің заңын оқу логика пәні болып табылады. Логика өз алдына ғылым болып грек философы Аристотельдің (384-322 ж. ж б. э. д) еңбегінде нақтыланған. Ол өзіне дейінгі мәліметтерді жүйеледі және осы жүйе кейін формальды немесе Аристотель логикасы деп аталды. Формальды логика еш өзгеріссіз 20 ғасырдай өмір сүрді. Математиканың дамуы Аристотель логикасының жетіспеушіліктерін көрсетті және оның әрі қарай дамуын талап етті. Математикалық негізде логиканы құру идеясын тарихта алғашқы болып неміс математигі Г. Лейбниц (1646-1716) XVI ғ. аяғында айтты. Ол логиканың негізгі ұғымдарын арнайы шарттармен байланысқан символдармен белгіленуі тиіс дейді. Бұл кез-келген ойларды есепке ауыстыруға мүмкіндік береді. Алғашқы болып Лейбництің айтуын жүзеге асырған ағылшын ғалымы Д. Буль (1815-1864) . Ол айтылымдар әріптермен белгіленген алгебраны құрды және бұл айтылымдар алгебрасын дүниеге әкелді. Логикаға симвлодық белгілеуді ендіру, бұл ғылымға маңызды болды. Дәл осы символдарды логикаға ендіру жаңа математикалық логика ғылымының негізін қалады. Логикада математиканы қолдану логикалық теорияларды жаңа формада кқруге мүмкіндік берді және есептеуіш аппараттарды адамның ойлау қабілеті жетпейтін есептерді шешуде қолдану логиканың зерттеу облысын кеңейтті. XIX ғ. аяғында математика үшін актуальді мәнге ие болатын сұрақтар туындады, яғни оның негізгі ұғымдары мен идеялары бойынша. Бұл мәселенің логикалық негізі болды және бұл математикалық логиканың әрі қарай дамуына алып келді. Бұл қатынаста неміс математигі Г. Фреге (1848-1925) және Итальян математигі Д. Пеано (1858-1932) еңбектерінде көрсетілген. Математикалық ойлаудың ерекшеліктері математикалық абстракция және олардың байланыстарының түрлілігінің ерекшеліктерімен түсіндіріледі. Осыған орай осы заманғы математикалық логиканы математиканың бөлімі ретінде қарастырады. Математикалық логиканың дамуының негізгі себептерінің бірі әртүрлі математикалық теорияларды құруда аксиоматикалық әдістердің кең таралуы болып табылады. Математикалық теорияны аксиоматикық құруда алдын-ала кейбір белгісіз жүйе ұғымы және олардың арасындағы қатынас тандалады. Осы ұғымдар мен қатынастар негізгі деп аталады. Әрі қарай дәлелдеусіз теория қарастыратын негізгі орын аксиома қолданылады. Барлық алдағы теорияның мазмұны аксиомадан логикалық түрде шығарады. Математикалық теорияда аксиоматикалық құруды алғашқы болып геометрияны құруды Эвклид қолданды. Бұл теория алғашқыда әлсіз түсіндірілді. Эвклид мұнда негізгі ұғымдарға (нүкте, түзу, жазықтық) анықтама бергісі келді. Теорияны дәлелдеуде еш жерде жинақталмаған орын қолданылды. Теорияны аксиоматикалық құру тәсілі XIX ғ. дейін жалғыз болды. Осы әдісті өзгертуде Н. И. Лобачевский (1792-1856) еңбектерінің маңызы зор болды. Лобачевский алғашқы болып Евклидтің 5 постулатының дәлелденбейтінін айтты және осы айтуын жаңа геометрияны құруда нақтылады. Кейін неміс математигі Ф. Клейн (1849-1925) Лобачевский геометриясын дәлелдеді. Осылайша математика тарихында олардың еңбектері алғашқы болып аксиоматикалық теорияның ділелденбейтін мәселесі көрсетілді. Математиканы негіздеудің басқа тәсілдері Д. ГИЛБЕРТ (1862-1943) және оның мектебінде дамытылды. Олар математикалық теорияны құруды синтаксистік теория негізіне сүйене отырып құрды. Осылайша, математикалық теорияның қарсылықты еместігін дәлелдеу басқа математикалық теория пәні болды, оны Гильберт математика немесе дәлелдеу теориясы деп атады. Осы тұрғыда синтаксистік, яғни фромальданған аксиоматикалық теорияны математикалық логика негізін құру мәселесі туындайды. Әртүрлі тәсілмен аксиома жүйесі және басқа формуланы шығару шартын таңдауда әртүрлі синтаксистік логикалық теорияны аламыз. Олардың әрқайсысын логика есептелімі деп атаймыз.
І ТАРАУ. ТҰЖЫРЫМДАР АЛГЕБРАСЫ
1. 1. Тұжырым ұғымыБүкіл математикадағы сияқты, біздің курстағы әр бөлімде де бастапқы негізгі ұғымдар бар. Негізгі ұғымдар анықталмайды. Біздің әрқайсысымыздың олар туралы ішкі түсінігіміз бар деп есептеледі. Бұл ішкі түсініктерде математикалық білім саласындағы адамзаттың тарихи тәжірибесі жинақталған. Негізгі ұғымдар анықталмайды, оларға квазианықтамалар, яғни басқа анықталған ұғымдар мен объектілерге сілтеме жасайтын анықтамалар беріледі. Бірінші бөлімде мұндай негізгі анықталған ұғым тұжырымдар болып табылады.
Тұжырым деп - ақиқатығы немесе жалғандығы туралы айтуға болатын байланысты баяндамалы сөйлемді айтамыз.
Мысал 1. «2*2=4» (екі көбейту екі тең төрт) .
Мысал 2. «Егер натурал сан 6ға бөлінсе, онда ол 3ке бөлінеді».
Мысал 3. Тауық қүс емес.
Мысал 4. 3≥5.
1 және 2 тұжырымдар - ақиқат, ал 3, 4 -жалған. Бір ғана тұжырым болатын айтылымды жай немесе қарапайым деп атайды. Қарапайым тұжырымға мысал болып 1 тұжырымды айтуға болады. Граматикалық байланыстар көмегімен («және», «немесе», «егер . . . , онда . . . », «сонда тек сонда ғана») құрылған тұжырымдарды күрделі деп атайды. Осылайша 2 тұжырым мынадай қарапайым тұжырымдардан тұрады: «натурал сан 6 бөлінеді», «натурал сан 3 бөлінеді». 4 тұжырым «немесе» сөзімен қосылған «3 үлкен 5» және «3 тең 5» тұжырымдар. Әрі қарай бізді тұжырымдардың мағыналы жағы қызықтырмастан, олар қандай ақиқаттық («ақиқат» немесе «жалған») мәнге ие болатындығы қызықтырады. Тұжырымдар алгебрасында бірдей ақиқаттық мәні бар барлық тұжырымдар алмасымды, яғни бізде ақиқат тұжырым және жалған тұжырым секілді екі тұжырым класы бар.
Қарапайым тұжырымдары латын алфавиттің a, b, c, …, x, y, z, … әріптерімен, ақиқат мәнді А әріппен немесе 1 цифрмен, жалған мәнді Ж әріппен немесе 0 цифрмен белгілейміз.
Егер а ақиқат болса, онда а=1 , ал егер жалған болса, а=0 деп жазамыз.
1. 2. Тұжырымдарға қолданылатын логикалық амалдар. Терістеуа тұжырымының терістеуі жаңа тұжырым болып табылады, бұл тұжырым а ақиқат болғанда жалған, ал а жалған болғанда кезде, ақиқат болады.
a
терістеу тұжырымы
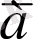 (¬
a
) деп бегіленеді және «
а
емес» немесе «дұрыс емес
а
» деп оқылады. ¬
a
тұжырымының логикалық мәнін кесте арқылы көрсетуге болады:
(¬
a
) деп бегіленеді және «
а
емес» немесе «дұрыс емес
а
» деп оқылады. ¬
a
тұжырымының логикалық мәнін кесте арқылы көрсетуге болады:
Бұл түрдегі кестені ақиқаттық кестесі деп атайды.
Мәселен, «2 кіші 5тен» тұжырымы үшін терістеу болып «2 кіші емес 5тен» тұжырымы болады.
а
тұжырым болсын.
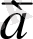 да тұжырым болғандықтан,
да тұжырым болғандықтан,
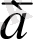 тұжырымына терістеу құруға болады, яғни
тұжырымына терістеу құруға болады, яғни
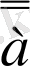 тұжырымы
а
тұжырымына екілік терістеу болады.
тұжырымы
а
тұжырымына екілік терістеу болады.
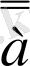 және
а
тұжырымдарының логикалық мәні бірдей.
және
а
тұжырымдарының логикалық мәні бірдей.
a және b тұжырымдарының конъюнкциясы деп, егер екі тұжырым да ақиқат болғанда ақиқат және егер кем дегенде біреуі жалған болғанда жалған болатын жаңа тұжырымды айтамыз.
a және b тұжырымдарының конъюнкциясы мына символмен белгіленеді a ∧ b ( a ּ b, a b, a & b) және былай оқылады « a және b» . a , b тұжырымдары конъюнкция мүшелері деп аталады. a және b екі тұжырымның барлық мүмкін логикалық мәндерінің конъюнкциясы келесі ақиқат кестеде көрсетілген:
Мысалы: «6 2-ге бөлінеді», «6 3-ке бөлінеді» тұжырымы үшін оның конъюнкциясы «6 2-ге бөлінеді және 6 3-ке бөлінеді» тұжырымы болады, бұл ақиқат. Конъюнкция операциясы анықтамасында көрсетілгендей «және» сөзі логика алгебрасында күнделікті сөйлесудегі сияқты мағынада қолданылады. Бірақ кәдімгі сөйлесуде «және» сөзімен мағынасы әртүрлі екі тұжырымды біріктіру қабылданбаған, ал логика алгебрасында кез-келген екі тұжырым конъюнкциясы қарастырылған.
1. 4 Дизъюнкцияa және b тұжырымдарының дизъюнкциясы деп, егер екі тұжырымның бірі ақиқат болса, ақиқат және егер екеуі де жалған болса, жалған болатын жаңа тұжырымды айтамыз.
a, b тұжырымдардың дизъюнкциясы мына символмен белгіленеді: a ∨ b және былай оқылады « a немесе b ». a, b тұжырымдары дизъюнкция мүшелері деп аталады.
a және b екі тұжырымның барлық мүмкін логикалық мәндерінің дизъюнкциясы келесі ақиқат кестеде көрсетілген:
1. 5 Эквиваленция
a және b екі тұжырымдарының эквиваленциясы деп егер тұжырымдар бірдей ақиқат немесе жалған болса, ақиқат, ал қалған жағдайларда жалған болатын жаңа тұжырымды айтамыз.
a және b тұжырымдарының эквиваленциясы мына символмен белгіленеді: a~b ( a↔︎b ) және былай оқылады: “ a үшін қажетті және жеткілікті b ” немесе “ a сонда және тек сонда ғана, қашан b ”. a, b тұжырымдары эквиваленция мүшелері деп аталады. a және b екі тұжырымның барлық мүмкін логикалық мәндерінің эквиваленциясы келесі ақиқат кестеде көрсетілген:
Мысалы: «S төбесі және PQ негізімен берілген SPQ үшбұрышы тең бүйірлі болады, сонда және тек сонда ғана, қашан
 P=
P=
 Q» эквиваленциясы ақиқат. “ S төбесі және PQ негізімен берілген SPQ үшбұрышы тең бүйірлі” және “ S төбесі және PQ негізімен берілген SPQ үшбұрышында
Q» эквиваленциясы ақиқат. “ S төбесі және PQ негізімен берілген SPQ үшбұрышы тең бүйірлі” және “ S төбесі және PQ негізімен берілген SPQ үшбұрышында
 P=
P=
 Q ” тұжырымдары бір мезгілде ақиқат немесе жалған.
Q ” тұжырымдары бір мезгілде ақиқат немесе жалған.
Эквиваленттілік математикалық дәлелдеуде үлкен роль атқарады. Теоремалардың белгілі бөлігі қажетті және жеткілікті формада құрылады, яғни эквиваленттілік формасында. Бұл жағдайда оның екі элементінің бірі ақиқат немесе жалған екенін біле отырып және эквиваленттіліктің өзінің ақиқаттығын дәлелдеп біз эквиваленттіліктің екінші мүшесінің ақиқат немесе жалған екенін қорытындылаймыз.
1. 6 Импликацияa және b екі тұжырымның импликациясы деп, егер a ақиқат, ал b - жалған болса жалған және қалған жағдайда ақиқат болатын жаңа тұжырымды айтамыз. a, b тұжырым импликациясы былай белгіленеді a→ b ( a ⊃ b a ⇒ b ) және былай оқылады “егер a , онда b ” немесе « a дан b шығады». а тұжырымын шарт немесе сілтеме тұжырым, ал b тұжырымын - салдары немесе қорытынды деп атайды. a және b екі тұжырымның барлық мүмкін логикалық мәндерінің импликациясы келесі ақиқаттық кестеде көрсетілген:
Мысалы, “егер 12 6-ға бөлінсе, онда ол 3-ке бөлінеді” тұжырымы ақиқат. Мұнда ақиқат сілтеме және ақиқат қорытынды. Импликация математикалық дәлелдеуде үлкен роль атқарады. Теоремалардың белгілі бөлігі қажетті және жеткілікті формада құрылады. Егер бұл жағдайда a ақиқат болып және a→ b импликацияның ақиқаттығы дәлелденген болса, онда b салдардың ақиқат екенін қорытындылаймыз. Логикалық амалдармен алғаш танысқанда импликациядан басқаның барлығы мейлінше табиғи түрде енгізілген секілді. Ал импликация анықтамасын енгізуді қабылдауға біздің санамыз қарсылық көрсетіп жатқандай болып көрінеді. Бірақ импликацияның мұндай анықтамасы біздің түйсікті ішкі логикамызға және математикада өте жиі қолданылатын «егер …, онда ххх» конструкциясына сәйкес келетіндігін көрсететін мысал келтіруге болады. Арифметикадан бір теореманы еске түсірейік - Q( x ) = «Егер х натурал саны 4-ке бөлінсе онда, ол 2-ге бөлінеді». Бұл теореманың әділдігіне біз күмән келтіреміз, яғни Q( x ) - қа қандай х натурал санын қойсақ та біз ақиқат айтылым аламыз. Белгілеу енгіземіз: А( х ) = « х натурал саны 4-ке бөлінеді», В( х ) = « х натурал саны 2-ге бөлінеді». Сонда шығатыны:
Q(x ) = А(x ) → В(x ) (1)
(1) формулаға х=8, 2, 3 мәндерін қоя отырып келесілерді аламыз: 1→ 1, 0→1, 0→ 0. (1) формулаға 1→ 0 шарты орындалатындай х -тің мәнін қою мүмкін емес (себебі келтірілген теорема әділ) .
Қарапайым тілде «Егер А, онда В» түрдегі сөйлемде А мен В мазмұны жағынан байланысты екенін көреміз. Біздің импликация анықтамасында бұл мүлде міндетті емес. Яғни біз мынадай импликацияны қарастыру құқымыз бар: «Егер бүгін бейсенбі болса, онда 2*2=5», бұл бейсенбіден басқа барлық күні ақиқат, ал бейсенбіде жалған.
1. 7 Тұжырымдар алгебрасының формулаларыТұжырымдарға қолданылатын логикалық амалдары көмегімен берілген тұжырымдардан күрделі тұжырымдарды құруға болады. Операциялардың орындалу реті жақшамен көрсетіледі. Мысалы, x, y, z үш тұжырымдарынан мынадай тұжырымды құруға болады:
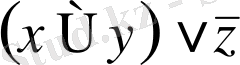 және
және
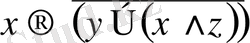 .
.
Қарапайым тұжырымдардан терістеу, конъюнкция, дизъюнкция, импликация және эквиваленция логикалық амалдарды қолдану көмегімен алынған күрделі тұжырым тұжырымдар алгебрасының формуласы деп аталады.
Тұжырымдар алгебрасының формулаларын латын алфавиттің бас әріптерімен белгілейміз: A, B, C, …, X, Y, Z, … Жазуды жинақтау үшін формулалардағы амалдарды ретімен орындау келісілген. Басқа барлық операциялардан бұрын конъюнкция орындалады, ал дизъюнкция импликация мен эквиваленттік бұрын орындалады. Бұл амалдардың орындалу ретін анықтайтын жақшалар қойылмауы мүмкін. Егер кейбір формуладан немесе ішформуладан терістеу алынса, ол жағдайда да жақша қойылмайды.
Демек, жоғарыда келтірілген
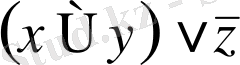 және
және
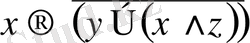 формулаларды былай жазуға болады:
формулаларды былай жазуға болады:
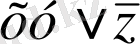 және
және
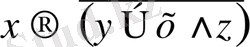
немесе
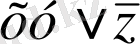 және
және
 .
.
Логика алгебрасында формуланың логикалық мәні оған кіретін қарапайым тұжырымдардың логикалық мәндерімен толығымен анықталады. Мысалы, x=1, y=1, z=0 болғанда ¬(x∧y) ∨¬z формуланың логикалық мәні ақиқат болады, яғни ¬(x∧y) ∨¬z =1.
Логикалық амалдар сияқты, формуланың барлық мүмкін болған мәндері оның ақиқаттық кестесі көмегімен берілу мүмкін.
Мысалы, ¬x∨y→х∧¬у формуласы үшін ақиқаттық кестесінің көрінісі төмендегідей:
1
1
0
0
1
0
1
0
0
0
1
1
0
1
0
1
1
0
1
1
0
1
0
0
0
1
0
0
Егер формуланың құрамына n қарапайым тұжырым енетін болса, онда ол нөл және бірден тұратын 2 n мән қабылдайды немесе формуланың ақиқаттық кестесі 2 n қатардан тұрады деп айтуға болады.
1. 8 Тұжырымдар алгебрасының пара-пар, тепе-тең ақиқат және тепе-тең жалған формулаларыЕгер логика алгебрасының А және В формулалары олардың құрамына енетін қарапайым тұжырымдарының кез келген мәндерінде бірдей мән қабылдаса, онда бұл формулалар пара-пар деп аталады. Формулалардың пара-парлығын ≡ белгісімен белгілейміз, яғни
А ≡В ⇔ А және В формулалары пара-пар.
Егер А формуласы оған кіретін айнымалылардың барлық мәндерінде 1 мәнді қабылдайтын болса, онда бұл формула тепе-тең ақиқат (немесе тавтология ) деп аталады.
Егер А формуласы оған кіретін айнымалылардың барлық мәндерінде 0 мәнді қабылдайтын болса, онда бұл формула тепе-тең жалған (немесе қарама-қайшылық ) деп аталады.
2 тарау. тұжырымдар есептелімі 2. 1 Тұжырымдар есептелімі формуласының ұғымыТұжырымдар есептелімі бұл интерпретациясы тұжырымдар алгебрасы болатын аксиоматикалық логикалық жүйе. Әрбір есептелімнің сипаттамасына бұл есептелімі символдарының, формулаларының сипаттамасы, дәлелденетін формулалардың анықтамасы енеді.
Тұжырымдар есептелімінің алфавиті үш түрлі символдардан тұрады:
1.
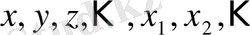 Бұл символдарды айнымалы тұжырымдар деп атаймыз.
Бұл символдарды айнымалы тұжырымдар деп атаймыз.
2.
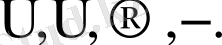 Бұл символдар логикалық байланыс деген жалпы атауға ие. Келтірілген символдардың біріншісі дизъюнкция (немесе логикалық қосу) белгісі, екіншісі - конъюнкция (немесе логикалық көбейту) белгісі, үшіншісі - импликация және төртіншісі - терістеу белгісі.
Бұл символдар логикалық байланыс деген жалпы атауға ие. Келтірілген символдардың біріншісі дизъюнкция (немесе логикалық қосу) белгісі, екіншісі - конъюнкция (немесе логикалық көбейту) белгісі, үшіншісі - импликация және төртіншісі - терістеу белгісі.
3. Жақшалар деп аталатын символдар: (, ) .
Тұжырымдар есептелімінде басқа символдар болмайды. Тұжырымдар есептелімінің формуласы тұжырымдар есептелімі алфавитінің символдарының тізбегі болады. Формула белгісі үшін латын алфавитінің үлкен әріптерін қолданамыз. Олар өздері есептелімнің символдары болмай, формулалардың тек шартты белгілері болады.
Тұжырымдар есептелімі формуласының анықтамасы
1. Кез келген
айнымалы формула болады. 2. Егер А және В - формулалар болса, онда
сөздер де формулалар.
3. Ешқандай басқа символдардың қатары формула болмайды.
Айнымалы тұжырымдарды қарапайым формулалар деп атаймыз.
Тұжырымдар есептелімі формуласына мысал келтірейік.
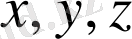 айнымалы тұжырымдар анықтаманың 1-ші бөлімі бойынша формулалар болады. Бірақ, онда
айнымалы тұжырымдар анықтаманың 1-ші бөлімі бойынша формулалар болады. Бірақ, онда
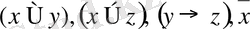 сөздер де анықтаманың 2-ші бөлімі бойынша формулалар бола алады. Сол себепке байланысты
сөздер де анықтаманың 2-ші бөлімі бойынша формулалар бола алады. Сол себепке байланысты
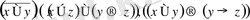 сөздер де формула бола алады.
сөздер де формула бола алады.
Формула түсінігі мен бірге ішформула немесе формула бөлігі түсінігі енгізіледі.
1. Қарапайым формуланың ішформуласы оның өзі болады.
2. Егер формула
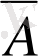 көрінісінде болса, онда оның ішформулалары формуланың өзі, А формуласы және А формуланың барлық ішформулалары болады.
көрінісінде болса, онда оның ішформулалары формуланың өзі, А формуласы және А формуланың барлық ішформулалары болады.
3. Егер формула (А*В) (мұнда * -
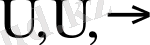 үш символдардың бірі деп түсінеміз) көрінісінде болса, онда оның ішформулалары формуланың өзі, А, В формулалары және А мен В формулалардың барлық ішформулалары болады.
үш символдардың бірі деп түсінеміз) көрінісінде болса, онда оның ішформулалары формуланың өзі, А, В формулалары және А мен В формулалардың барлық ішформулалары болады.
Формуладағы логикалық амалдарының саны формуланың рангі деп аталады.
2. 2. Дәлелденетін формула ұғымыТұжырымдар есептелімінің құруда келесі кезең дәлелденетін (шығарылатын) формулалардың класын бөліктеу болады. Дәлелденетін формула анықтамасы формулалар анықтамасы сияқты. Алдымен бастапқы дәлелденетін шығарылатын формулалар (аксиомалар) анықталады, ал содан кейін бар дәлелденетін формулалардан жаңа дәлелденетін формулаларды алуға мүмкіндік беретін шығару ережелері анықталады. Бастапқы дәлелденетін формулалардан шығару ережелерін қолдану көмегімен жаңа дәлелденетін формуланы алу процесі берілген формуланы аксиомалардан шығаруы (дәлелдеуі) деп аталады.
2. 3 Тұжырымдар есептелімінің аксиомалар жүйесіТұжырымдар есептелімінің аксиомалар жүйесі Аксималардың бірінші тобы (құрамыларыны тек импликация енеді) .
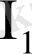 :
:
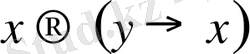 .
.
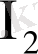 :
:
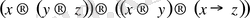 .
.
Аксималардың екінші тобы ( импликацияға конъюнкция қосылды) :
 :
:
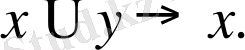
 :
:
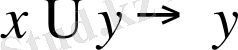 .
.
 :
:
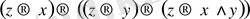 .
.
Аксималардың үшінші тобы ( импликацияға дизъюнкция қосылды) :
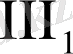 :
:
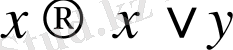
 :
:
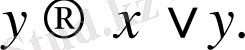
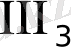 :
:
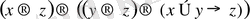 .
.
Аксималардың төртінші тобы (импликацияға терістеу қосылды) :
 :
:
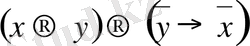
 :
:

Анықтама 1 . x 1 , x 2 , …, x n - пәндік айнымалылардың символдары болсын. Пәндік айнымалылардың (x 1 , x 2 , …, x n ) топтары пәндік аймақ деп аталатын Ω жиыныны тиісті болсын. Ω пәндік аймағында анықталған n-орынды предикат деп, Ω-ның тұжырымдар жиынына бейнелеуін айтады.
Мысалдарды қарастырар алдын n-орынды предикаттарға квазианықтама берейік:
Анықтама 2.
«
n
айнымалыға тәуелді және келесі қасиетке ие болған баяндамалы байланысты сөйлемі: айнымалылардың орнына анық мәндер қойылғанда ақиқат немесе жалған болсын».
Мысал 1.
D(x
1
, x
2
)
= «
x
1
натурал саны
x
2
натурал санына бөлінеді (қалдықсыз)
» -
N
 N
жиынында анықталған екі орынды предикат. Түсінікті,
D(4, 2) =1, D(3, 5) =0
.
N
жиынында анықталған екі орынды предикат. Түсінікті,
D(4, 2) =1, D(3, 5) =0
.
Мысал 2.
Q(x) = «х
2
<-1, x
 R»
-
R
нақты сандар жиынында анықталған бір орынды предикат.
Q(-1) =0, Q(
R»
-
R
нақты сандар жиынында анықталған бір орынды предикат.
Q(-1) =0, Q(
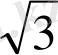 ) =0
.
Q(x)
- тепе-тең жалған екендігі түсінікті, яғни
Q(x)
) =0
.
Q(x)
- тепе-тең жалған екендігі түсінікті, яғни
Q(x)
 0
.
0
.
Мысал 3. R(x, y, z) = «x
2
+ y
2
 z; x, y, z
z; x, y, z
 R»
-
R
3
жиынында анықталған үш орынды предикат
. R(1, 1, -2) =0, R(1, 1, 2) =1
.
R»
-
R
3
жиынында анықталған үш орынды предикат
. R(1, 1, -2) =0, R(1, 1, 2) =1
.
Мысал 4.
S(x, y) = «sin2ху>-3; x, y
 R»
- екі орынды тепе-тең ақиқат предикат.
R»
- екі орынды тепе-тең ақиқат предикат.
Р(x 1 , x 2 , …, x n ) - Ω аймағында анықталған n-орынды предикат болсын. Онымен келесі түрде анықталған екі жиынды байланыстырамыз:
I P ={( x 1 , x 2 , …, x n ) ∈ Ω Р(x 1 , x 2 , …, x n ) =1} - Р предикаттың ақиқаттық жиыны ,
L P ={( x 1 , x 2 , …, x n) ∈ Ω Р(x 1 , x 2 , …, x n ) =0} - Р предикаттың жалғандық жиыны .
Анықтама 2. Р - Ω-да анықталған предикат болсын. Егер I P = Ω (L P =∅) болса, онда Р тепе-тең ақиқат , егер L P = Ω (I P =∅) болса, онда Р тепе-тең жалған предикат деп аталады.
Егер I P ≠ Ω және L P ≠ ∅ болса, онда Р орындалатын предикат деп айтамыз.
R 3 кеңістікте 3 мысалдағы R(x, y, z) предикаттың I P және L P жиындарын көрсетейік (1 сурет) .
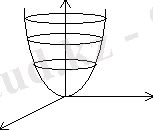 z
I
P
z
I
P
1 сурет
3. 2 Предикаттарға логикалық амалдарды қолдану ... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz