Күрделі электр тізбектерін үшбұрыш-жұлдыз түрлендіру әдісімен есептеу


Тақырыбы: Күрделі тізбектерді «үшбұрыш» - «жұлдыз» түрлендіруі арқылы есептеу
ЖОСПАР:
Кіріспе:
Электротехниканың қолданылуы.
«Үшбұрыш» - «жұлдыз» түрленуінің техника қолданылуы.
Негізгі бөлім:
- Кирхгоф заңдарына түсініктеме.
- «Үшбұрыш» - «жұлдыз» түрлендірілуі.
- «Үшбұрыш» - «жұлдыз» түрлендірілуіне мысал есеп.
- Жалпы кедергі табу
- Жалпы және жеке ток күштерін табу.
Қорытынды.
КІРІСПЕ
Электроэнергетика саласы көптеген өндірісте, көлікте ауыл шаруашылығында және күнделікті өмірде кеңінен қолданылады.
Электротехника деп бұл сөздің кең мағынасында электромагнитті құбылыстарды тәжірибеде қолдану болып танылады.
Электротехниканың дамуы электрлік және оның тәжірибелік бейнесін жасау және оны оқып үйрену үлкен жұмысты қажет етті.
А. Вольттың гальваникалық бағананы ойлап тапқаннан кейін электр тогын алу мүмкін болды. Электр тізбегін В. В. Петров зерттей келе, электр доғасын ашты және оның жарықтандыру, балқыту және металдарды біріктіру тәжірибелерінде қолдануға болатынын көрсетті.
1845 жылы немістің атақты физигі, әрі технигі Г. Кирхгоф тармақталған электр тізбектеріне негізгі заңдары жасалып шықты және ол заңдар осы атақты кісінің атымен аталып, электротехниканың теориялық және практикалық дамуына үлкен үлес қосып келеді.
Көптеген қазіргі уақыттағы әр түрлі техникалық жетістікке арналған электротехникалық қондырғыларға түрлі түрлендірулер қолданылады. Электр генераторлары мен двигательдер, механикалық және электрлік энергияға түрлендіру үшін қызмет етеді. Трансформатордың көмегімен бір электр энергиясының кернеуі екінші электр энергиясының кернеуіне айналады. Электр шамында электр энергиясының жарық энергиясына түрлендіру процесі жүріп отырады. Көптеген электротехникалық қондырғыларда электр энергиясы осы қондырғының бөлек элементтерінің арасында бөлінеді.
Осындай көп жақты түрлендіру практикалық жағынан ғана пайдалы болып қоймай, түрлендіру кезіндегі, жалпы электр тізбегін есептеу оңайлана түседі. Сол түрлендірудің маған, яғни осы курстық жұмысты жазудағы негізгі міндет, «үшбұрыш» және «жұлдыз» деп аталатын схемалы контурларды, электр тізбектерін, біріншісі күрделі болғанда екіншісіне түрлендіріп немесе керісінше екінші түрден бірінші түрге айналдырып есепті шешудің теориялық сондай-ақ, практикалық маңызы өте зор болып табылады, бұл электротехникада кеңінен қолданылады. Бұл түрлендіру оның ішінде күрделі тізбектерді «үшбұрыш» - «жұлдыз» түрлендіруі арқылы есептеу менің осы курстық жұмысымның нігізгі мақсаты болып табылады.
Кирхгофтың екі заңы, кейде оны Кирхгоф ережелері деп те атайды, күрделі электр тізбектерін есептеу үшін және толығымен олардың электр қалыптарын анықтау үшін қолданылады. . Күрделі тізбектер үшін тармақ, түйін және контур түсініктерін қолданады.
Электр тізбектерінің тармағы - бойынан сол ток өтетін және тізбектей қосылған элементтерден - резисторлардан, ток көздерінен және т. б. тұратын тізбек бөлігі.
Электр тізбегінің түйіні - үш және одан да көп тармақтардың қосылған орны, жері.
Электр тізбегінің контуры - бірнеше түрлі тармақ арқылы өте алатын кез-келген тұйықталған жол.
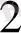
1 суретте үш тармақтан тұратын тізбек көрсетілген, ол ток көзінен Е, екі түйіннен және үш контурдан құралады.
Кирхгофтың бірінші заңы (ток заңы) электр тізбектерінің түйініне қатысты. Осы заңға сәйкес түйіннен бағытталған кез-келген элкетр тізбегінің
Тоқтарының қосындысы, түйінге бағытталған ток қосындысына тең. 1 суретте I=I
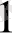 +I
+I
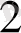 . Басқаша сөзбенен айтқанда, кез-келген тізбектегі түйіннің тоқтарының алгебралық қосындысы нөлге тең.
. Басқаша сөзбенен айтқанда, кез-келген тізбектегі түйіннің тоқтарының алгебралық қосындысы нөлге тең.
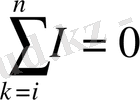
Түйіннен бағытталған оң токтар деп және түйінге бағытталған токтарды оң ток деп есептесек 1 суретте
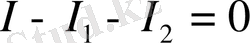 немесе
немесе
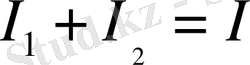 .
.
Кирхгофтың бірінші заңы стационарлы қозғалыстың нәтижесінде құрылатын ток кезіндегі элементарлық бөліктердің сақталу қағидасынан шығады.
Кирхгофтың бірінші заңы және Ом заңы ортақ өткізгіштік және резисторлардың параллельді қосылуы анықталады. Егер резисторлар екі сыңарлы (парлы) түйінге қосылған болса және
 сол бір кернеуде орналасса онда резисторлар параллельді қосылған.
сол бір кернеуде орналасса онда резисторлар параллельді қосылған.
Екі резистордың
 және
және
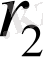 параллельді қосылған кезде бөлек түйіндегі ток Ом заңына сәйкес
параллельді қосылған кезде бөлек түйіндегі ток Ом заңына сәйкес
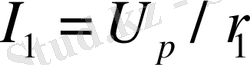 ;
;
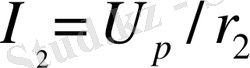 болады.
болады.
Сәйкесінше
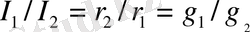 , яғни параллельді қосылуда ток кедергіге кері пропорционал және тармақ өткізгішіне тура пропорционал.
, яғни параллельді қосылуда ток кедергіге кері пропорционал және тармақ өткізгішіне тура пропорционал.
Кирхгофтың бірінші заңын басшылыққа ала отырып энергия көзінің тогы
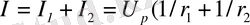 .
.
 кернеуі ортақ тармақталмаған тогына қатынасы тармақталған кедергіні анықтайды, яғни эквивалентті резисторлар кедергісі барлық қалған тізбек бөлігіндегі электр шарты екі параллельді қосылған кездегі резисторлардың орнына қосылғанда өзгермейді.
кернеуі ортақ тармақталмаған тогына қатынасы тармақталған кедергіні анықтайды, яғни эквивалентті резисторлар кедергісі барлық қалған тізбек бөлігіндегі электр шарты екі параллельді қосылған кездегі резисторлардың орнына қосылғанда өзгермейді.
Тармақталған эквивалентті кедергі
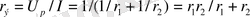 .
.
Жалпы жағдайда бірнеше параллельді қосылған резисторлар кезіндегі жалпы ток
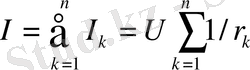 .
.
Үш резисторлардың
 ,
,
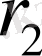 ,
,
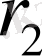 параллельді қосылуы кезінде эквивалентті кедергі мынадай
параллельді қосылуы кезінде эквивалентті кедергі мынадай
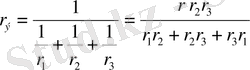 .
.
Тармақталу үшін Ом заңын қолдану оңайланады, егер кедергілерді сәйкес өткізгіштермен ауыстырса
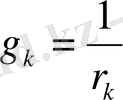
Екі резистордың параллельді қосылуы үшін Ом заңы осындай өзгерістен кейін мына формаға келеді:
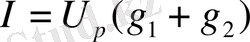 ,
,
ал жалпы түрде
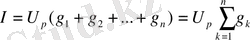 .
.
Кирхгофтың бірінші заңын және Ом заңын қолдана отырып аралас қосылған резисторларды есептеуге болады. Тізбек тек бір ғана энергия көзінен тұрғанда оны көп жағдайда аралас қосылу деп қарастыруға болады, яғни бірнеше резисторларды параллельді қосылған, басқа резисторлармен тізбектей қосылған. 1 суретте
 және
және
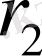 резисторларды парллельді жалғанған және r резисторымен тізбектей қосылған. Осындай тізбекті есептеу үшін біріншіден эквивалентті кедергілер тармақталуымен ауыстыру керек, ал содан кейін тізбекті екі резистордың тізбектей жалғануы деп қарастыру қажет. Эквивалентті кедергінің тармақталуы:
резисторларды парллельді жалғанған және r резисторымен тізбектей қосылған. Осындай тізбекті есептеу үшін біріншіден эквивалентті кедергілер тармақталуымен ауыстыру керек, ал содан кейін тізбекті екі резистордың тізбектей жалғануы деп қарастыру қажет. Эквивалентті кедергінің тармақталуы:
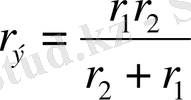 .
.
Енді тізбектей r және
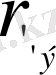 тізбектей қосылған деп қарастыруға болады. Жалпы ток:
тізбектей қосылған деп қарастыруға болады. Жалпы ток:
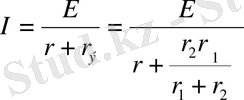 .
.
Тармақталған түйіндер арасындағы кернеу:
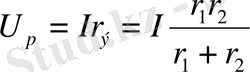 болады
болады
және Ом заңына байланысты екі тармақтағы ток
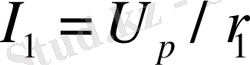 және
және
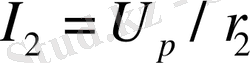 .
.
1 сурттегі схемада бір кездегі көздің өткізгіш сымдар арқылы екі қабылдағышқа (
 және
және
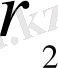 ) энергия беруі көрсетілген деп есептеуге болады, мұндағы
) энергия беруі көрсетілген деп есептеуге болады, мұндағы
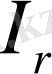 -- өткізгіш сымындағы кернеудің төмедеуі,
-- өткізгіш сымындағы кернеудің төмедеуі,
 -- энергия қабылдағыштарындағы кернеу (мысалы, электр шам) .
-- энергия қабылдағыштарындағы кернеу (мысалы, электр шам) .
Кирхгофтың екінші заңы электр тізбегінің тұйық контурдағы тепе-теңдікті бейнелейді. Осы заңға сәйкес кез-келген тұйық контурындағы ЕҚК алгебралық қосындысы осы контурға кіретін резисторлар кернеулерінің басқа сөзбен айтқанда ЕҚК алгебралық суммасы кедергілерге сәйкес осы контур бөлігіндегі токтардың алгебралық суммасының қосындысына тең,
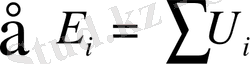
Бұл теңдіктегі оң мәнді деп ЕҚК мен токты санауға болады, сондағы бағыттары қарастырылып отырған контурдың ойша таңдалып алынған бағыты сәйкес тура келеді.
Кирхгофтың екінші заңы, кез-келген тізбек нүктесіндегі потенциалы тізбектегі орнымен анықталады дегеннен шығады. Ол Кирхгофтың екінші заңының келесі түрде жазылуында айқын көрініп тұр:
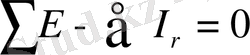 ,
,
яғни тұйық контурды айнала қозғалғанда потенциалдың өзгеруі алгебралық суммасы нөлге тең, себебі кез-келген тұйық контурды айналғаннан кейін біз қалыптағы нүктеге қайта ораламыз, яғни потенциалға.
Кирхгофтың екінші заңын қолдану екі және одан да көп электр көздерінен тұратын электр тізбектерін есептеу үшін қажет. 2 суреттегі (схемадағы) токтарды есептегенде Кирхгофтың екі заңдары бойынша құрылатын теңдеулер үшін қажет.
Түйіндер үшін теңдеулер құрылғанда тәуелсіз теңдеулер саны m түйіндерде бір бірлікке аз болатынын ескеру керек, яғни ол теңдеулер саны m-1 тең; бұл шарт әр тармақтың екі рет түйінге кіретіні белгілі, өйткені әрбір тармақ екі түйінмен қосылады. Соңғы түйіндегі токтың теңдеуіне, басқа түйін теңдеулеріне кірген, токтар ғана кіретін болады. Тізбекті есептеу үшін бұл теңдеудің қажеттілігі жоқ. Мысалы, 2 суреттегі қарапайым тізбек тек а және b түйіндерінен құралған және ол үшін Кирхгофтың бірінші заңы бойынша тек бір ғана тәуелсіз теңдеу болады, а түйіні үшін
-
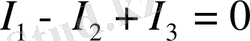 ,
,
және b түйіні үшін
-
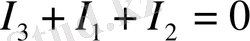
яғни бұл да тек сол токтардан тұрады.
Кирхгофтың екінші заңы бойынша теңдеулер жазғанда өтілген контурға қосылмаған бір тармақтан кем емес әрбір келесідегі контурға кіретін контур айналысын таңдау керек. n тармақ саны белгісіз ток санына тең. Осы n токты анықтау үшін Кирхгофтың бірінші заңына сәйкес теңдеулер анықталып қойды. Сәйкесінше токтарды есептеу үшін Кирхгофтың екінші заңына сәйкес тағы n-m+1 теңдеулер жазу керек. 2 суреттегі схема үшін n=3, m=2 Кирхгофтың екінші заңы бойынша теңдеулер саны n-m+1=3-2+1=2. Бұл теңдеулер:
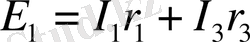
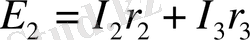 .
.
Бұл схемадағы үшінші контур басындағы екі контурға кірген түйіндері бар, сондықтан
 теңдеуін есептеу үшін керегі жоқ.
теңдеуін есептеу үшін керегі жоқ.
Сонымен n белгісіз теңдеулерін анықтау үшін n теңдеулерді бірігіп шешу үшін құрайды. Егер белгілі мәндерді қойғаннан кейін токтардың біреуінің мәні теріс шама болса, онда шынындағы ток бағыты есепті шешудегі басында берілген бағытқа қарама - қарсы.
Осы сияқты сәйкес теңдеулер жүйесін шешу көп уақытты алады, сондықтан күрделі электр тізбектерін есептеу үшін арнайы есептеу әдістері қолданылады, бірақ оның барлығы теориялық жағынан Кирхгофтың екі заңына сүйенеді.
Электр тізбектерінінің теориясында есептің екі түрі шығарылады. Оның біріншісіне тізбектін конфигурациясы және элементтері белгілі болғанда бірақ оның бір бөлігінің тогын, кернеуін және қуатын талдау есебі жатады, мысалы, ток пен кернеу берілген, бірақ тізбектің конфигурациясын және элементтерін таңдап табу болып табылады. Бұндай есептер электр тізбектерінің синтез есептері деп аталады.
Практикалық электротехникада талдау есептері жиі кездеседі. Одан басқа, тізбектердің синтез әдістерін қолдану үшін оған алдын-ала талдау әдістерін оқып, біліп алу қажет.
Талдау есептерін Кирхгоф заңдарының көмегімен шығаруға болады. Егер барлық тізбек элементтерімен және оның конфигурацияларының параметрлері белгілі болса, бірақ токты табу керек болса, онда Кирхгоф заңдары бойынша теңдеулер құрылған кезде мынадай қимыл қадамдарын ұстанған дұрыс болады: біріншіден, электр тізбегінің барлық тармақтарының ойша оң таңбамен алынған оң бағыттарын таңдап алып, содан кейін Кирхгоф заңдарына сәйкес түйіндерге теңдеулер құру керек және контурлар үшін Кирхгофтың екінші заңына сүйеніп теңдеулер құрылады.
Кирхгофтың екінші заңы бойынша теңдеулерді жазғанда құрылған теңдеулер бір-біріне тәуелсіз болуына ерекше көңіл бөлу керек. Контурды есептеу оған схемадағы барлық тармақтар кіріп, ал контурдың әрқайсысы - тармақ санынан кем болуы мүмкін. Егер теңдеу құрылатын әрбір келесі кем дегенде бір жаңа тармақ болса және ортақ тармақтарға өшіру арқылы құрылған теңдеулер болмаса контур бір-біріне тәуелсіз болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz