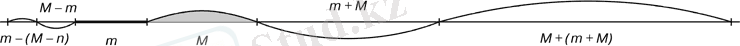Алтын қиманың геометриялық негіздері, тарихы және өнер мен табиғаттағы қолданылуы


Жоспары
І. Кіріспе
ІІ. Негізгі бөлім
1. Алтын қима пропорциясы. Ф және φ
2. Алтын қиманың тарихы
4. Пропорцияның құрылымы
5. Екінші алтын қима
6. Алтын пішіндер. Алтын тікбұрыш
7. Алтын үшбұрыш
8. Алтын бесбұрыш
9. Архимед серіппесі
10. Фибоначчи сандары
11. Алтын қима кескіндемеде
ІІІ. Қорытынды
Пайдаланылған әдебиеттер
Кіріспе
Ғылыми жұмыс өмірдің мазмұны мен мақсатына айналғанда ғана жемісті болмақ.
А. Ф. Иоффе
Қазақстанның орта білім жүйесінің алдында бүкіл адамзаттың құндылық тұғырнамасында қалыптасқан, тәні және жаны сұлу, өзіне-өзі сенімді, ғылыми-тоериялық білімділігі мен тәжірибелік қабілеттері арқылы күрделі әлемдік, өмірлік әрі әлеуметтік кеңістікке еркін ене алатын қасиеттерге ие дарынды тұлға тәрбиелеу міндеті қойылып отыр. Соның ішінде ғылыми зерттеу жұмысы - қазіргі заман біліміне сай ғылым болмақ.
Республикамыздың президенті Н. Назарбаев өзінің жолдауында әлемдегі ең озық 50 елдің қатарына кірігу стратегиясын айқындаған болатын. Сонымен бірге Елбасы Қазақстанның әлемдік экономикаға ойдағыдай кіруі бағытындағы басты міндеттерінің бірі- ғылым мен білім, жаңа технологиялар бәсекелестіктің шешуші факторы екендігін атап көрсетті.
Ғылыми зерттеу табандылықты, шыдамдылықты, көп ойлануды, сондай-ақ еңбекқорлықты талап етеді. Ғылыми зерттеу әрбір оқушыда сапалы және терең білім іскерліктің болуын, олардың шығармашылықпен жұмыс істеуін, ойлауға қабілетті болуын талап етеді. Оқушылардың өз бетімен жұмысын қалыптастыру оқушының ғылымға деген қызығушылығынан және қажеттілігінен туады. Сондай-ақ өз қызығушылығымнан туындаған «Алтын қима» тақырыбын зерделеу, оның қыр-сырларын ашып, ғылым негізінің бір жолына шығару мақсатым болмақ. «Талаптыға нұр жауар» демекші, қажымас қайрат, таусылмас талап болса, зерттеулердің көптеген сырларын аша алатынымызды естен шығармауымыз керек.
Мақсаты:
Алтын қима туралы мағлұматпен толық танысып, оның қазіргі кездегі қолданысын зерттеу.
Міндеті :
- «Алтын қима» тақырыбын зерттей отырып, негізгі теориясымен танысу;
- зерттеу жұмысын корректі түрде құрастыра білу және зерттеулердің нәтижелеріне геометриялық тұрғыдан баға беру;
Нысаны:
«Алтын қиманы» геометриялық тұрғыдан зерттеу.
Өзектілігі:
Зерттеліп отырған жұмыс білім алуды жалғастыруға қажетті нақты математикалық білімді меңгеруге, интелектіні дамытуды, математикалық іс-әрекетке тән және қоғамда толыққанды қызмет етуге қажетті зерттеу сапасын қалыптастыруға мүмкіндік береді.
Проблемасы:
«Алтын қиманың» қазіргі кездегі қолданысын және музыка, сәулет өнері, кескіндемедегі қолданысын зерттеу.
Болжамы:
Егер «Алтын қима» туралы мағлұматпен толық таныссам,
онда алған білімімді өмірде қолдана аламын, интеллектілігім және тәжірибелік іскерлігім дамиды.
Зерттеу кезеңдері:
- «Алтын қиманы» әдебиеттерден іздеу, сұрыптау;
- «Алтын қима» туралы мәліметтерді қосымша интернет жүйесінен іздеу, жобалау;
- Табылған мәліметтерді Power Point арқылы суреттеу;
Тәжірибенің әдістемесі:
Қазіргі өмірде әлеуметтік жағдайдың барлық салаларын жан-жақты зерттеу нәтижесінде жасөспірім ұрпақтың жан-дүниесін сол негізде тәрбиелеп, оның бойындағы оянбай жатқан қасиеттерді жандандыру - өмір талабы.
Зерттеу жұмысының жаңалығы: Өскелең ұрпақтың біліктілігін қалыптастыруға бағытталған жаңа зерттеулердің негізінде білімді жетілдіру талаптарын күрделендіруге негізделген.
Нәтижесі:
- білім алуды жалғастыруға қажетті математикалық білімді меңгереді;
- интеллектіні дамытады;
- математикалық іс-әрекетке тән және қоғамда толыққанды қызмет етуге қажетті ойлау сапасын қалыптастырады;
Алтын қима пропорциясы. Ф және φ
«Геометрия екі ұлы қазынаға ие. Оның бірі - Пифагор теоремасы, екіншісі - кесіндіні шеткі және орта қатынаста бөлу. »
Дұрыс көпбұрыштарға Архимедке дейінгі көне грек ғалымдары да өте үлкен назар аударған. Пифагорлықтар, өздерінің одақтас әмблемамен таңдаған пентаграммасын - бес бұрышты жұлдызды және шеңберді бірдей бірдей бөліктерге бөлуге арнады. Альбрехт Дюрер Германиядан алып келген дұрыс бес бұрышты құру туралы нақты теориясын Птолемейдің ұлы «Альмагест» шығармасымен одақтастырды.
Дюрердің дұрыс бесбұрышты қолданылу қызығушылығы орта ғасырда арабтық және готикалық оюларда, қамал тұрғызуда және дәрімен атылатын қару-жарақ құрастыруда көрінеді.
Леонардо до Винчи көпбұрыштар туралы көп жазғанымен, тек қана Дюрер
ұрпаққ ортағасырлық құрастыруларды қалдырған. Әрине Дюрер Евклидтің (циркуль және сызғыштың көмегімен тұрғызулар) «Бастамасымен» таныс болған, бірақ өзінің «Өлшеулі басшылығына» кіргізген жоқ. Евклид берілген доғаны үш бөлікке бөлуге тырыспайды,
ал бұны Дюрер білген. Бұл тапсырма шешілмейтіндігінің дәлелі ХІХ ғасырда табылған.
Евклид ұсынған дұрыс бесбұрыштың құрылысы ортаңғы және шеткі қатынастағы дұрыс кесінді бөлігін енгізеді, ол нәтижесінде алтын кесінді деп аталып, бірнеше жүздеген жылдар бойы өзіне сәулетшілер мен архитекторлардың назарын аударып келген. [1]
Егер кесіндінің үлкен бөлігінің кіші бөлігіне қатынасы барлық бөліктің үлкен бөлігіне қатынасына тең болса, Е нүктесі АВ кесіндісін орта және шеткі қатынастарда бөледі немесе алтын қима жасайды.
Жазылған алтын қима қатынастарының теңдігі мынандай түрде белгіленеді:
АЕ/ВЕ = АВ/АЕ
Алтын қатынастың АЕ/ВЕ = Ф теңдігіне тең болу үшін, АЕ=а, ал ВЕ=
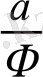 деп аламыз.
деп аламыз.
Онда
Ф=1+1/Ф
деген қатынасқа тең болады. Яғни, Ф
Ф 2 -Ф-1=0
теңдеуін қанағаттандырады. Бұл теңдеудің бір ғана дұрыс түбірі болады:
Ф=(
+1) /2 = 1, 618034 . . .
1/Ф үшін φ=0, 618034 . . . , 1/Ф=(
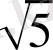 -1) /2, яғни (
-1) /2, яғни (
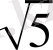 -1) (
-1) (
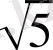 +1) =5-1=4 екенін ескеріміз. .
+1) =5-1=4 екенін ескеріміз. .
Ф және φ - гректің жазбаша және баспаша түрі.
Бұндай мағына көнегрек мүсіншісі Фидияның атымен аталған. Фидия
Афинадағы Парфенон храмының құрылысын басқарған. Бұл храмның пропорциясында φ саны көп кездеседі.
Алтын қиманың тарихы
Алтын бөлу туралы түсінікті ежелгі грек философы және математигі Пифагор, өзінің ғылыми күнділігіне енгізген. Пифагор алтын бөлу туралы ілімді мысырлықтар мен вавилондықтардан алған деген жорамал бар. Бұған Хеопс пирамидасының пропорциясы, храмдардың, бетмүсіндердің, тұрмыс заттарының және Тутанхамона моласындағы әдемілеулер куә. Египтік шеберлер осыларды жасауда да алтын бөлуді қолданған. Француз сәулеткері Ле Корбюзье Сети І Абидос фараонның хрмындағы рельефтен және Рамсес фараонын бейнелеуші рельефтен пішіндердің пропорциялары алтын бөлудің шамаларына сәйкес екенін анықтады. Ағаш тақтайдан жасалған молада бейнеленген Зодчий Хесир, алтын бөлу пропорциясы жазылған өлшеу аспаптарын ұстап жатыр.
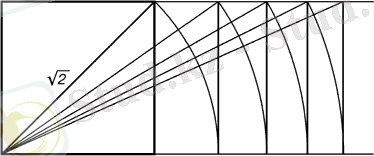
Гректер де шебер геометрлер болған. Өз балаларын арифметиканы геометриялық фигуралардың көмегімен оқытқан. Пифагордың квадраты және осы квадраттың диагоналі динамикалық тікбұрыштар құруда негіз
болған.
Платон да алтын бөлу туралы білген. Оның «Тимей» диалогі Пифагордың математикалық және эстетикалық көзқарастарына арналған, алтын бөлу сұрағы ретінде қалған.
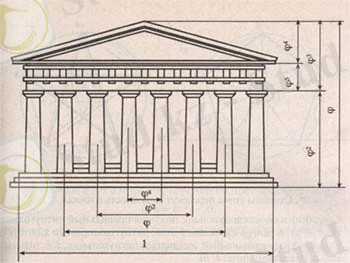 Парфенон қысқа жағынан 8 бағана және ұзынынан 17 бағанадан құралған. Ғимараттың биіктігінің ұзындығына қатынасы 0, 618- ге тең. Егер Парфенонның «алтын қимасымен» бөлсек, онда сол немесе сол сияқты фасадтардың түрлерін аламыз. Оның жанын қазған кезде көне әлем сәулетшілері мен мүсіншілері пайдаланған циркульдер табылды. Помпей циркульінің өзі алтын бөліктерге пропорцияланған.
Парфенон қысқа жағынан 8 бағана және ұзынынан 17 бағанадан құралған. Ғимараттың биіктігінің ұзындығына қатынасы 0, 618- ге тең. Егер Парфенонның «алтын қимасымен» бөлсек, онда сол немесе сол сияқты фасадтардың түрлерін аламыз. Оның жанын қазған кезде көне әлем сәулетшілері мен мүсіншілері пайдаланған циркульдер табылды. Помпей циркульінің өзі алтын бөліктерге пропорцияланған.

Бізге жеткенге дейінгі көне әдебиеттердің ішіндегі Евклидтің «Бастамасында» алтын бөлулер бірінші рет еске түсіріледі. «Бастаманың» 2-ші кітабында алтын бөлудің геометриялық сызбалары берілген. Евклидтен кейін алтын бөлудің зерттеулерімен Гипсикл, Папп және т. б. айналысқан. Орта ғасырлық Еуропа Евклид «Бастамасының» алтын бөлуімен араб аудармаларынан танысты.
Қайта өрлеу заманына орайлас ғалымдардың және суретшілердің арасында алтын бөлуді қолдану деген ұғым күшейді, ол геометрияда қалай қолданылса, сәулет өнерінде де, өнерде де солай қолданылды. Суретші және ғалым Леонардо до Давинчи, итальяндық сәулетшілерде өте үлкен тәжірибе бар, бірақ білімдерінің жетіспейтіндігін көрді. Ол ойланып, геометрия туралы кітап жаза бастады, бірақ сол кезде монах Луки Пачолидің кітабы шықты, содан соң Леонардо өзінің бұл ойын тастады. Замандастардың және ғылым тарихшыларының ойы бойынша, Лука Пачоли нағыз жарық, Фибоначчи мен Галлилейдің арасындағы Италиядағы ұлы математик. 1509 жылы Венецияда
Лука Пачоллидің өте күшті көркемдеулерімен жасалған «Божестевенная пропорция» атты кітабы жарық көреді, бірақ оны Леонардо до Винчи жасады
деген пікір бар. Кітап алтын пропорцияның қуанышты әнұраны болды. Леонардо до Винчи өзінің көңілін алтын бөлу зерттеуіне де
бөлген. Ол дұрыс бес бұрыш жасайтын стереометриялық денеге қима жасаған, және әр кез қабырғалардың алтын бөлуге қатынасындай тікбұрыш алған. Сондықтан ол алтын бөлуді алтын қима деп атаған.
Сол кездері солтүстік Еуропадағы Германияда осы мәселелермен Альбрехт Дюрер де айналысқан. Дюрер: « Біреу бірдеңе білсе мұқтаж болғандарға оқыту қажет. Осыны істеуге менің ниетім ауды» деп жазды.
Дюрердің хаттарына қарағанда, ол Италияға барған кезде Лука
Пачолли мен кездескен секілді. Альбрехт Дюрер адам денесінің пропорциясы теориясын толық өңдеді. Дюрер өзінің бұл жүйесінде алтын қиманың негізін көрсете білді. Дюрердің пропорционалдық циркулі бізге өте мәлім.
Алтын пропорцияның кесінділер қатарын ұлғаю жағына, сонымен қатар азаю жағына қоюға болады.
Егер түзу ұзындықтарға m (φ) кесіндісін қойса, қатарына М кесіндісін ығыстарымыз. Осы екі кесінді негізінде алтын пропорцияның ұлғаю және азаю қатарларының кесінді шкаласын салуға болады.
Алтын пропорция кесіндісінің құрылу шкаласы
Кейінгі ғасырларда алтын пропорция ережесі академиялық
қағидаға айналды. 19 ғ-дың ортасын жаңа алтын қиманы зерттейтін неміс профессоры Цейзинг «Эстетические иследования» атты еңбегін жариялады. Ол алтын қима пропорциясы табиғаттың барлық құбылыстарына және өнерге әмбебап арнап, оны абсолюттеген. Цейзингтің көптеген ізбасарлары және қарсыластары болды. Ол пропорция туралы ғылымын «Математикалық эстетика» деп жариялаған.
Пропорцияның құрылымы
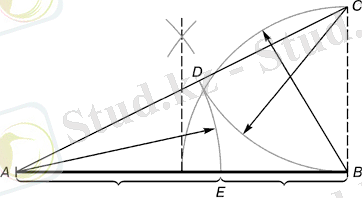
Кесіндіні алтын қима қатынасында бөлу.
ВС = 1/2АВ; СД=ВС
Кесіндіні алтын қима пропорциясымен бөлетін Е нүктесі жүргізіледі. В нүктесінен АВ кесіндісінің қақ ортасынан бөлінетін перпендикуляр жүргізіледі. Алынған С нүктесі А сызығымен қосылады. Алынған кесіндіден Д нүктесінен аяқталатын ВС кесіндісі кейінге қалады. АД кесіндісі тікелей АВ кесіндісіне теңгеріледі. Осыдан алынған Е нүктесі АВ кесіндісін алтын пропорция арақатынасында бөледі.
Дәл осы кесінділерді Евклид өзінің дұрыс бесбұрыш жасауында қолданылды.
Осыған байланысты жұлдызды бесбұрышта сонымен қатар «алтын қима» қолданылады. Бір қызықтысы бесбұрыштың ішінен бесбұрыш жасап жалғастырсаң, оның қатынастары сақтала береді. Сайып келгенде, жұлдызды бесбұрышта сонымен қатар «алтын қима» қолданылған.
Жұлдызды бесбұрыш пентаграмма деп аталады. Пифагорлықтар өздерінің талисмандары ретінде бесбұрышты жұлдызды таңдады. Ол денсаулықтың символы мен танымдылықтың белгісі ретінде қызмет еттді.
Қазіргі уақытта гипотеза бар, оның ең бірінші мағынасы пентаграмма, ал екінші мағынасы «алтын қима». Пентаграмманы ешкім ойлап тапқан жоқ, оны тек көшіріп алды. Бесбұрышты жұлдыздың жеміс ағаштарындағы гүлдердегі бес жапырақ, теңіз жұлдызы тәрізді түрлері бар. Және құбылыстарды табиғат жаратылымдарын адамдар қанша мың жыл бақылап келеді.
Сол себепті, объектілердің геометриялық бейнелеулері - пентаграмма - ертеректен белгілі.
Екінші алтын қима
Болгарлық «Отечество» атты журналда Цветана Цекова-Карандашаның негізгі қимадан шығатын және 44:56 қатынаста бөлетін «Екініші алтын қима» атты мақаласы жарияланды.
Мұндай пропорция сәулет өнерінде де табылды, сонымен қатар ол ұзартылғын горизантальдық формат бейнелеулерінің композицияларын құруда орын алады.
Бөлу келесі бейнемен жүзеге асады. АВ кесіндісі алтын қима пропорциясында бөлінеді. С нүктесінен СД перпендикуляры жүргізіледі. Радиус АВ-ның ортасында А нүктесіне түзу арқылы жүргізілген Д нүктесі орналасқан. АСД тікбұрышы қақ ортасынан бөлінеді. Е нүктесі АД кесіндісін 56:44 қатынаста бөледі.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz