Токтар, кернеулер, қуаттар, магнит ағымдары

Пән: Электротехника
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Қазақстан республикасы білім және ғылым

министрлігі

Қолданбалы информатика кафедрасы

Курстық жұмыс

Тақырыбы: Параллел тізбекті емес тізбектер

Орындаған:

Тексерген:

МАЗМҰНЫ

Көп сәулелі жұлдызша жалғанған кедергілерді көпбұрышты етіп жалғауға түрлендіру ұшбұрышты, жұлдызшаға түрлендіру . . . 2
ЭҚК-тері және ток көздері бар тармақтарды параллель жалғағандағы

жүргізілетін түрлендіру . . . 5

ЭҚК бар схеманы, эквивалентті ток көзі схемасына түрлендіру . . . 7
Теңгеру (компенсация) жайындағы теорема . . . 9
Активті екі ұшты теоремасы . . . 10
Энергияны активті екі ұштыдан пассивті екі ұштыға беру . . . 12

КІРІСПЕ

Қазіргі уақытта электр энергиясы барлық өнеркәсіп салаларында, транспортта, ауылшаруашылығында, ұй тұрмысында, тағы басқа халықтың тұрмыс қажеттілігіне кеңінен пайдаланады.

Электр техникасы деп электр магниті құбылыстарын практика жүзінде кең салада қолдануын айтамыз. Барық электр техникасы салалары бір-бірімен байланысты болғандықтан, техникалық жоғарғы оқу орындарында «Электр техникасының теориялық негіздері» курын ашуға тура келді. Бұл курс әр түрлі электр техникасы пәндерінің негізкі базасы болып есептелінеді.

Осы курстың негізгі бір міндеті, олқұбылыстарды токтар, кернеулер, қуаттар, магнит ағымдары тағы басқа түсініктер арқылы есептеу, зерттеу. Сондай-ақ тағы бір атқаратын міндеті ол құбылыстарды электр кернеулігі, магнит өрісінің идукциясы, қуат ағымдары тағы басқа түсініктер арқылы есептеу, зерттеу. Осы міндеттердің біріншісі тізбектерді, ал екіншісі электр магниті өрістерін есептеуге, зерттеуге арналған.

Электр техникасының өсіп-дамуы электр магниті құбылыстарын жете зерттеуді, оқып білуді, практика жүзінде пайдалануды керек етеді. Осы зор еңбекте, ізденуде көптеген жаңалықтарды ашуда орыс инженерлерінің, ғалымдарының қосқан үлесі аз емес. Олар шет елдердің көнекті ғалымдарымен бірлесе отырып електр техникасының маңызды саларыныңбастамасына жол ашты. Осы бастаманы бастағандардың бірі - М. Б. Ломоносов. Ол атмосфера электрі атты теориясын құрды. Заттың салмағының сақталу және қозғалыс заңдарын ашты.

А. Вольта (Италия физигі) ойлап тапқан гальваникалық элементтер бағанасынан кейін электр тогын алуға мүмкіншілік туды. 1802 жылы В. В. Петов электр тізбегіндегі процестерді зерттеп электр доғасын ашты және осыларды іс жүзінде жарық шығаруға, металды балқытуға, металдарды пісіріп жалғастыруға пайдалануға болады деген көз қарасын айтты.

Ағылшын ғалымы М. Фарадей 1831 жылы электр магниттік индукция заңын және оның құбылыстарын ашып, дамуына зор үлес қосты.

1883 жылы орыс академигі Э. Х: Ленц индукциялық токтардың бағыттарының араларындағы заңдылықты ашты және олардың электр магниттік, электр динамикалық байланыстарының бар екендігін ашты. Соның ішінде электр магниттік индукциясы негіздерін де ашты. 1844 жылы ол ағылшын зерттеушісі Джоульға тәуелсіз сым темір арқылы ток өткенде шығатын жылу мөлшері сол сымның кедергісіне және сондағы токтың квадратына тура пропорционал екенін анықтады. Әлемде бірінші рет Россияда П. Л. Шилинг1832 жылы электр магниті телеграфын түрғызды.

1845 жылы неміс физигі Г. Кирхгов тармақталған электр тізбектеріне арналған негізгі заңдарды ашты, сонымен ол заңдар Кирхгов атымен аталды.

1976 жылы орыс ғалымы П. Н. Яблочков элетр шамын ойлаптапты, одан бастап электремн жарықтандыру басталды. Бірінші көмір стерженді қызды рғыш шамын орыс инженері А. Н. Лодыгин құрастырғаны баршаға мәлім.

1. Көп сәулелі жұлдызша жалғанған кедергілерді көпбұрышты етіп жалғауға түрлендіру ұшбұрышты, жұлдызшаға түрлендіру

n-сәулелі жұлдызша жалғанған кедергілерді көпбұрышты эквивалентті схемасына түрлендіруде n(n-1) /2 тең тармақтарын аламыз.

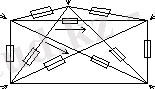1. 26а-суретте көп сәулелі жұлдызша жалғанған кедергілер бейнеленген. Осы схема үшін электрлік күйіне байланысты теңдеулер құрылады. Oм заңы бойынша тармақтардағы тоқтарды көрсетеді.

1-сурет. Кедергілерді түрлендіру схемалары.

\[{\cal I}_{1}=(j_{\ 1}-\phi_{0})g_{1};\]

\[I_{2}=(j_{\ 2}-\phi_{\mathrm{o}})\,g_{\mathrm{2}};\]

\[{\cal I}_{3}=(j_{\ 3}-\phi_{\mathrm{o}})\,g_{3};\]

(1. 1)

\[I_{4}=(j_{\mathrm{\Large~4}}-\phi_{0})\,g_{4}\,;\]

\[{\cal I}_{5}=(j_{\ s}-\phi_{\mathrm{o}})\,g_{5};\]

Кирхгофтық бірінші заңына теңдік жазады да (1. 1) ток мәндерін ауыстырып қойды.

\[\begin{array}{l}{{I_{1}+I_{2}+I_{3}+I_{4}+I_{5}=(j_{\ \ 1}-j\mathbf{\beta}_{0})g_{1}+(j_{\ \ 2}-j\mathbf{\beta}_{0})g_{2}+}}\\ {{+(j_{\ 3}-j\mathbf{\beta}_{0})g_{3}+(j_{\ \ 4}-j\mathbf{\beta}_{5}-\phi_{0})g_{5}=0}}\end{array}\]

(1. 2)

Мұндағы

\[\dot{\bar{J}}\;_{1}.\dot{\bar{J}}\;_{2}.\dot{\bar{J}}\;_{3}.\dot{\bar{J}}\;_{4}.\dot{\bar{J}}\;_{5}.\phi_{0},\]

- схеманың тиісті нүктелеріндегі потенциалдар. Соңғы теңдеуден С нүктедегі потенциялды табамыз.

\[j_{\phi}=\frac{j_{1}g_{1}+j_{\ 2}g_{2}+j_{\ 3}g_{3}+j_{\ 4}g_{4}+\phi_{5}g_{5}}{g_{1}+g_{2}+g_{3}+g_{4}+g_{5}}\]

(1. 1) теңдеуде мәнін ауыстырады.

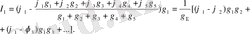
Мұндағы

\[g_{\mathrm{L}}=\sum g_{k}=g_{1}+g_{2}+g_{3}+g_{4}+g_{s};\]

\[k=1,2,3\dots\]

Алынған формулаға потенциалдар айырымын нүктелер арасындағы 1, 2, 3, . . . , . . . кернеу арқылы ауыстырылады.

\[U_{\it{n i}}=j_{\it{n}}-\phi_{i}\]

\[{\cal I}_{1}=U_{12}\,\frac{g_{1}g_{2}}{g_{\,S}}+U_{13}\,\frac{g_{1}g_{3}}{g_{\,S}}+U_{14}\,\frac{g_{1}g_{\,4}}{g_{\,S}}+U_{15}\,\frac{g_{\,1}g_{\,5}}{g_{\,\Sigma}};\]

(1. 3)

ұқсастық бойынша кез келген ток үшін

\[{\cal I}_{n}=U_{n1}{\frac{g_{n}g_{1}}{g_{\mathrm{s}}}}+U_{n2}{\frac{g_{n}g_{2}}{g_{\mathrm{s}}}}+U_{n3}{\frac{g_{n}g_{3}}{g_{\mathrm{s}}}}+U_{n4}{\frac{g_{n}g_{4}}{g_{\mathrm{s}}}}+U_{n5}{\frac{g_{n}g_{5}}{g_{\mathrm{s}}}};\]

(1. 4)

Осы теңдеуден n-сәүлелі жұмызша жалғанған әр тармақтардағы тоқты жеке токтардың қосындысы түрінде көрсетуге болады. Олар тиісті нүктелер арасындағы кернеулерге пропорционал болып келеді. Мысалы, ток

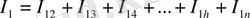
мұндағы

\[I_{13}=U_{13}\,{\frac{g_{1}g_{3}}{g_{\mathrm{L}}}}\]

және ұқсастық бойынша, кез-келген тармақтағы ток үшін

\[I_{h}=I_{h1}+I_{h2}+I_{h3}+I_{h4}+...+I_{h h}+....+J_{h n}\]

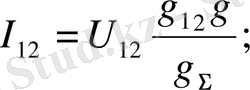
(1. 3-1. 4) формулалар 1 б-суреттегі n(n-1) тармақтар санына тең толық көпбұрыш түрінде келтірілген эквивалент схемасын қанағаттандырады. 1 б-схемасы үшін

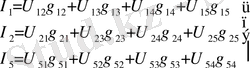(1. 5)

1 б-суреттегі схема 1 а-суреттегі схемаға эквивалентті болу үшін екі схемадағы бірдей кернеулердің салдарынан (

\[\textstyle{\cal O}_{12}\mathcal{O}_{13^{\ast}\ast}\mathcal{O}_{13}\]

) токтардың (

\[f_{1},J_{2},J_{3},\]

және т. б. ) теңдігі қажетті. Келесі көріністің орындалуы арқасында, жоғарғы шарттық та орындалады.

\[g_{12}=g_{1}g_{2}/g_{\mathrm{s}},g_{13}=g_{1}g_{3}/g_{\mathrm{s}},....\]

(1. 6)

Көпбұрыштың түйін саны n-тең байланысты ток, саны n-1 тең және әрбір тармақ көпбұрыштың екі түйінімен жағасқан, сонда олардың тармақ сандары n(n-1) /2 тең. Демек, n-сәулесі жұлдызша жалғанғансхемасы, көпбұрышты схемаға түрлендіргенде (1, 6) теңдеуді пайдаланады ал көпбұрыштың n-сәулелі жұлдызша жалғанған схемаға түрлендіру кері есеп болып саналады, жалпы жағдайда n>3 есептің шешімі табылмайды, өйткені іздестіріліп отырған эквивалентті жұлдызша жалғанған тармақтардың кедергілер (немесе өткізгіштер) саныn(n-1) /2 санынан аз. Шарт бойынша (n-1) /2 қанағаттандыруға тиісті.

n=3 уақытында шар саны n(n-1) /2=3 тең, олай болса үшбұрыш кедергілері әрқашан эквивалентті жұлдызщаға түрлендіруге болады.

(1, 6) теңдеуде 3 кезінде үш сәуле жұлдызды эквивалентті үшбұрышқа тура түрлендіріледі, эквивалентті өткізгіштер үшін:

\[g_{12}=\frac{g_{1}g_{2}}{g_{1}+g_{2}+g_{3}};g_{23}=\frac{g_{2}g_{3}}{g_{1}+g_{2}+g_{3}};g_{31}=\frac{g_{3}g_{1}}{g_{1}+g_{2}+g_{3}}\]

(1. 7)

немесе эквивалентті кедергілер үшін:

\[R_{12}=\frac{1}{g_{12}}=R_{1}+R_{2}+\frac{R_{1}R_{2}}{R_{3}},R_{23}=R_{2}+R_{3}+\frac{R_{2}R_{3}}{R_{1}},R_{31}=R_{3}+R_{1}+\frac{R_{3}R_{1}}{R_{2}}\]

(1. 8)

Тек берілген кедергілерімен

\[R_{12},R_{23},R_{31}\]

үшбұрышты, эквивалентті жұлдызшаға түрлендіру формуласын алу үшін (1, 8) теңдігінен белгісіз кедергілері ретінде

\[R_{1},R_{2},R_{3}\]

қабылдайды.

Қорыта келгенде,

\[R_{1}={\frac{b}{R_{23}}};R_{2}={\frac{b}{R_{31}}};R_{3}={\frac{b}{R_{12}}}\]

, мұндағы

\[b=R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}={\frac{b}{R_{23}}}{\frac{b}{R_{31}}}+{\frac{b}{R_{31}}}{\frac{b}{R_{12}}}+{\frac{b}{R_{12}}}{\frac{b}{R_{23}}}\]

(1. 9)

Алған формула түрлерін, в-формуласына ойын алмастырсақ, сонда

\[b=b^{2}\,{\frac{R_{12}+R_{23}+R_{31}}{R_{12}R_{23}R_{31}}}\]

мұндағы

\[b={\frac{R_{12}R_{21}R_{31}}{R_{12}+R_{23}+R_{31}}}\]

соныңда (1, 9) формулаға қойып көпбұрыштан жұлдызшаға түрлендіруін аламыз:

\[R_{1}=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}};\]

\[R_{2}={\frac{{R_{12}R_{23}}}{{R_{12}}+{R_{23}}+{R_{31}}}};\]

\[R_{3}={\frac{{R_{3}}R_{11}}{{R_{12}}+{R_{23}}+{R_{31}}}}\]

(1. 10)

Осындай ұқсастықтарды пайдаланып активті көп сәулелі жұлдызшадан эквивалентті активті көпбұрышқа ауыстыруға болады. Тек, жоғарыдағы дәлелденілген (1, 1-1, 10) формулаларға ЭҚК-ін есепке алып отырса болғаны.

2. ЭҚК-тері және ток көздері бар тармақтарды параллель жалғағандағы жүргізілетін түрлендіру

Егер күрделі электр схемасында бір немесе бірнеше параллель жалғанған ЭҚК көздері бар тармақтар болса, әрбір ток, ЭҚК бар тармақтарды бір эквивалетті ЭҚК-не және эквивалентті ішкі кедергісіне ауыстырса, онда осындай схеманы есептеу және зерттеу жұмыстары әлдеқайда жеңілдейді. Жеке жағдайда схемада аралас жалғанған активті және пассивті эквивалентті кездессе оларды тізбектес жағанған осы элементтері бар схемаға түрлендіріледі. Параллель жалғанған токты тармақтарды бір эквиваленті тармаққа ауыстыру.

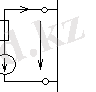
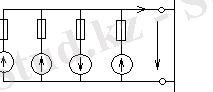
2-сурет. ЭҚК-дерін түрлендіру схемасы

2 а-суретте параллель жалғанған тармақтардан тұратын бір топ электр схема бөлігі келтірілген. Схеманың басқа бөліктері шарт бойынша тік бұрыш арқылы белгіленген. Параллель n тармақтарды бір эквивалентті тармаққа ауыстыру керек (2 б-сурет), ол үшін ток І және U эквивалент схемасындағы және басқа схема бөліктеріндегі токтар мен кернеулер мәндері, тек берілген схемадағыдай қалуға тиісті.

\[\begin{array}{l}{{I=I_{1}+I_{2}+...+I_{n}+I_{m}=(E_{1}\cdot U)g_{1}+(-E_{2}\cdot U)g_{2}+...+}}\\ {{+(E_{h}\cdot U)g_{h}+...+(E_{m}\cdot U)g_{m}=E_{1}g_{1}+E_{2}g_{2}+...+E_{h}g_{h}+...+}}\\ {{+E_{m}g_{m}-U(g_{1}+g_{2}+...+g_{h}+...+g_{m})}}\end{array}\]

(1. 11)

2 б-сурет схемасындағы ток І=(E-U) g (1. 12)

Мұндағы g=1/R;

\[E={\frac{E_{1}g_{1}+E_{2}g_{2}+...+E_{h}g_{h}+...+E_{m}g_{m}}{g_{1}+g_{2}+...+g_{m}}}={\frac{1}{g_{{\mathrm{S}}}}}\sum_{h=1}^{h=m}E_{h}g_{h}\]

(1. 13)

Эквивалентті ЭҚк-ң Е _h есептеп шығару кезінде Е ЭҚК-ін оң таңбамен жазуға болады, егер оның оң бағыты эквивалентті ЭҚК-мен бір түйінге бағытталса, сондай-ақ кері бағыттас болып басқа түйінге бағытталса теріс таңбамен жазылады. Егер параллель жалғанған тармақтың бірінде ЭҚК-і болмаса, мысалға, ЭҚК көзі Е ₃ болмаса, онда (1, 12) формулада Е ₃ g ₃ қосындысы болмайды, ал бөліміндегі өткізгіштер құрамына өткізгіш міндетті түрде кіреді.

Егер эквивалентті ЭҚК есептеу кезінде 1- және 2-түйіндерге (2 а-сурет) m тармақты ЭҚК-нен басқа тағы тармақтағы ток көздері берілген болса, онда олардағы токты есепке алу қажет.

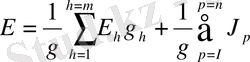(1. 14)

Ток бағыты эквивалентті ЭҚК-мен бағыттас болып бір түйінге бағытталса оң таңбамен жазылады, ал бағыттас болмаса теріс таңбамен жазылады.

3. ЭҚК бар схеманы, эквивалентті ток көзі схемасына түрлендіру

Энергия көздерін белгілі ЭҚК мәнімен және берілген ішкі кедергісін ток көзі арқылы көрсетуге болады, сонымен бірге энергия қабылдағыштарының іс тәртібі өзгеріссіз қалады.

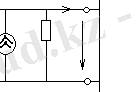ЭҚК көзін эквивалентті ток көзіне түрлендіру.

3-сурет. ЭҚК-нен ток көзіне ауысу схемасы

3 а-суретте ЭҚК көзінің ішкі кедергісі мен қысқыштың 1 және 2 буындарына жалғанған болсын және осы қысқыштар арасындағы кернеуге тең, онда ток

\[I={\frac{E-U}{R}}={\frac{E}{R}}-{\frac{U}{R}}=J-{\frac{U}{R}}=J-I_{B}\]

(1. 15)

мұндағы

\[J={\frac{E}{R}}\]

-ток көзі тогы

\[\displaystyle I_{\boldsymbol{B}}\]
- ішкі кедергілердегі ток.

\[\hat{J}\,\]
- ЭҚК көзі тогы, тек ЭҚК бар тармақтың параметріне байланысты табылған ток

көзі тогы мен

\[I_{B}={\cfrac{U}{R_{B}}}\]

тогының айырмасына тең. (1. 15) теңдеугеэквивалентті схемаға 3-сурет сайма-сай, ондағы кернеу

\[\textstyle\int\!\!{J}\,\]

және ток

\[\hat{J}\,\]

(3 а-суреттегі) схемадағы кернеу мен ток бірдей. Ток көзі тогы

\[\mathcal{J}\]

, ЭҚК бағытымен бір бағыттас.

Өзаралық қасиеттері немесе өзаралық принципі

Мына қасиеттің негізгі маңызы келесі келтірілгендей. Схемада еркін келген кескінде үйлесімінде (конфигурациясында) жалғыз ЭҚК көзі,

\[E_{q},R_{q}\]

-кедергісі бар тармаққа «в» нүктеден «а» нұктесіне қарай әрекет етіп бағытталған (4 а-сурет) және

\[\textstyle{\mathcal{P}}_{\mathcal{U}}\]

кедергілі тармақта «d» нүктеден «с» нүктесіне бағытталған

\[\frac{\sqrt{\vphantom{\Psi}}}{}_{l}\qquad\]

тогын туғызады.

Осы байланыстықты көрсететін схемалар.

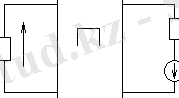
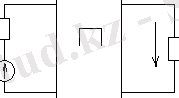
4 - сурет

Сонда осындай жалғыз ЭҚК көзін

\[E_{\iota}=E_{q},R_{\iota}\]

-кедергісі бар тармаққа қосса және әректтігі «d» нүктесінен «с» нүктесіне (4 б-сурет) бағытталса, сонда

\[\textstyle R_{\it q}\]

кедергілі тармақта ток

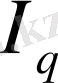туғызады, оның бағыты «в»-дан «а»-ға бағытталған және

\[\frac{\sqrt{\vphantom{\Psi}}}{}_{l}\qquad\]

тоғына тең,

\[I_{q}=I_{l}\]

болады.

4 а-суретте «ав» және «сd» тармақтары

\[\textstyle R_{\it q}\]

және

\[\textstyle{\mathcal{P}}_{\mathcal{U}}\]

кедергілері бейнеленген, ал схеманың басқа бөліктері энергия көзінсіз шартты түрде тік бұрыш ішіне енгізілген және «П» әрпімен белгіленген (Пассивті элементтерді көрсетеді) . Демек,

\[E_{q}\,=\,E_{l}\]

ЭҚК-тері бір-біріне тең болған жағдайда «сd» (4 а-сурет) және «ав» (4 а-сурет) тармақтарындағы токтар бір-біріне тең болады. өзаралық қасиеттерін контурлық токтар тәсілін пайдаланып дәлелдеуге болады.

Өзаралық қасиеті токтар үшін ғана әділетті болып қоймайды, сондай-ақ кернеу үшін дке әділеттіліктің сақталатыны көрінеді және Кихгоф заңдарын немесе түйіндік потенциалдар тәсілін пайдаланып осы әділеттіліктерді дәлелдеуге болады.

Өзаралық қасиеттерін пайдаланып кіре берістен

\[{\mathcal{G}}_{q q}\]

және

\[{\mathcal{G}}_{H}\]

өткізгіштігін және

\[{\mathcal{G}}_{l q}\]

мен

\[{\mathcal{G}}_{q l}\]

тармақтарының арасындағы өзара өткізгіштерді анықтайды. Кірер өткізгіштік, екі бірдей индекс арқылы

\[{\mathcal{G}}_{q q}\]

немесе

\[{\mathcal{G}}_{H}\]

, ал өзара өткізгіш-әртүрлі екі индекс арқлы

\[{\mathcal{G}}_{l q}\]

немесе

\[{\mathcal{G}}_{q l}\]

түрінде белгіленеді.

Өткізгітікке кері шама кедергі береді, сондықтан кіре берістегі тармақтағы кедергі

\[R_{q q}=\frac{1}{q_{q q}},R_{l l}=\frac{1}{g_{u}}\]

, ал өзара кедергі

\[R_{q l}=\frac{1}{g_{q l}},R_{l q}=\frac{1}{g_{l q}}\]

тең.

Кірер және өзара өткізгіштерінің сан мәндері және тармақталған кедергілері келесі жолмен анықталуы мүмкін. Қарастырылып отырған схемадағы

\[E_{h}\]

ЭҚК-нен басқа барлық ЭҚК-ін нөлге теңейді. Сонда, ток

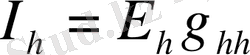(1. 16) мұндағы

\[g_{h h}=\frac{I_{h}}{E_{h}}=\frac{1}{R_{h h}}\]

кедергі өткізгіштігі. Сондықтан кез келген тармақтың кірер өткізгіштігі сол тармақтағы токтың ЭҚК-не қатынасы арқылы табылады. Басқа тармақтағы ЭҚК-нің нөлге тең кезінде, ал кірер кедергі өткізгіштікке кері шама.

Тармаққа қосылған ЭҚК жалпы алғанда барлық тармақтарда, жекелей алғанда тамағында ток туғызады.

\[J/I\]

тармақтардағы ток,

\[E_{\mathit{h}}\]

ЭҚК-нен басқа ЭҚК-тері нөлге тең болғанда

\[I_{m}\ =E_{h}\,\sigma_{m h}\]

мұндағы п

\[g_{m h}=\frac{I_{m}}{E_{h}}=\frac{1}{R_{m h}}\]

өзара өткізгіштігі.

\[\mathcal{\otimes}_{m h}\longrightarrow\mathcal{O}_{h m}\]

өзара өткізгіштіктердің теңдігін атап өту керек. Кез келген екі тармақтың өзара өткізгіштері бар тармақтағы токтың басқа тармақтағы ЭҚК-не қатынасы арқылы анықтайды, әрине барлық басқа тармақтадағы ЭҚК нөлге тең болған кезде. Сондай-ақ екі тармақ арасындағы өзара кедергі, сол тармақтардағы өзара өткізгіштеріне кері шамаға тең.

Кірер және өзара өткізгіштерді және де тармақ кедергілерін есептеуге немесе эксперимент арқылы табуға болады.

4. Теңгеру (компенсация) жайындағы теорема

5 а-суретте көрсетілген схемасында

\[\textstyle{\mathcal{P}}_{\mathcal{U}}\]

кедергісі және

\[{\underline{{\mathit{f}}}}_{l}\]

токгы бар тармақ бөлінген.

Осы тармаққа екі ЭҚК көзін

\[E_{1}^{1}\]

және

\[E_{1}\]

(5 б-сурет) енгізген. Олардың сан мәні

\[U_{1}=R_{1}I_{1}\]

кернеуіне тең және олардың бағыттары бір-біріне қарама-қарсы алынған, сонда токтар барлық тармақтарда өзгеріп қалады.

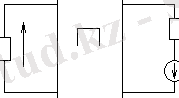Теңгеру теоремасын түсіндіруге арналған электр схемалары келтірейік.

5 -сурет. Теңгеру теоремасын түсіндіретін схемалар

Кез келген кедергіні ЭҚК көзіне ауыстыруға болады, оның бағыты ток бағытына қарама-қарсы және сол кедергідегі кернеуіне тең. Осы жағдайды теңгеру (компенсация) теоремасы дейді.

Ьұны дәлелдеу үшін (5 б-сурет) «d» нүктесінен «с» нүктесіне өткенде потенциал

\[E_{1}^{1}=U_{1}\]

шамасына көбейеді, ал «с» нүктеден «в» нүктесіне өткенде сол шамаға азаяды, осының салдарынан «d» және «в» нүктелеріндегі потенциалдар бір-біріне тең

\[U_{\ d}=U_{b}\]

, сондықтан осы нүктелерді өткізгішпен тұйық қосуға болады. 5 б-суретте үзілмелі сызықпен көрсетілгендей, яғни ЭҚК көзі

\[E_{1}^{1}=U_{1}\]

және

\[R_{1}\]

кедергісі схемадан алып тасталған, бұдан басқа барлық тармақтардағы ток өзгермейді немесе

\[j_{\mathrm{\footnotesize~b}}-j_{\mathrm{\Large~4}}=-\,R_{1}I_{1}+E_{1}^{1}=0;j_{\mathrm{\footnotesize~b}}=\phi_{d}.\]

5. Активті екі ұшты теоремасы

Күрделі электр схемасындағы процестерді зерттегенде, тек бір тармақтағы токты, кернеуді және қуатты табу керек болады. Ол үшін осы күрделі схемадан бір ғана тармақты бөліп шығарады. Осы бөлінген тармақ қысқыштары арқылы ЭҚК-тері бар күрделі тізбектің барлық қалған бөлігін бір ғана эквивалентті ЭҚК-мен және ішкі кедергісімен ауыстырылуы мүмкін. Бұдан былай оны активті деп, ал екі ұштыдан электр энергия көзі болмаса пассивті деп аталады. әртүрлі пассивті екі ұштыда электр энергиясын қабылдаушы деп саналады және бір ғана шама

\[\textstyle{\mathcal{D}}\]

кедергісімен бейнеленеді. Сондықтан эквивалентті схемада пассивтің екі ұшты және бір элемент

\[\textstyle R_{b}\]

-кедергісі арқылы көрсетіледі және оны пассив екі ұштының ішкі немесе кірер кедергісі деп аталады.

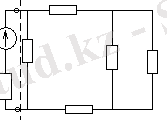
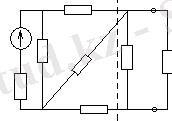Мысалы, 6 а-суреттегі схеманы қарастырайық. Екі ұштыларды түсіндіруге арналған схемалар.

6 - сурет. Екі ұштылар схемаларына түсіндірулер

Егер схемадан ЭҚК көзі және

\[R_{1}\]

-кедергісіне бар тармақты 2-2 қысқышы арқылы бөлсек үзілмелі сызығымен жүргізілген (басқа қалған бөлігін пассивті екі ұшты деп қарастырамыз. Сол схеманы 1-1 қысқышы

\[\textstyle R_{2}\]

кедергісі тармағы арқылы қарасақ 6 б-сурет) схеманың қалған бөлігі активті екі ұшты деп саналады (нүктелерден сызық жүргізілген) .

7 - сурет. Активті, пассивті екі ұштылар схемалары

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.