Квадраттық функциялар, квадрат теңдеулер және теңсіздіктер: теориясы мен шешу әдістері


Жоспар
Кіріспе . . . 2
І. Теңсіздік түрлері . . . 4
ІІ. Квадраттық теңсіздік.
2. 3. Квадраттық теңсіздік . . . 7
2. 4. Квадрат теңсіздіктерді шешу әдістері . . . 10
2. 5. Квадраттық фунция . . . 13
ІІІ. Квадрат теңдеулер . . . 16
Қорытынды . . . 24
Пайдаланылған әдебиеттер тізімі . . . 25
Кіріспе
Елбасымыз Н. Ә. Назарбаев ұсынған «Қазақстан-2050» стратегиясында негізгі бағыттардың бірі ретінде халықтың ұлттық моделі мен салт-дәстүрлерін есепке ала отырып, білімі мен білігі жағынан өркениетті елдердегі замандастарымен қатар тұра алатын, бойында ұлттық, отаншылдық рухы мықты қазақстандықтардың жаңа ұрпағын тәрбиелеу қажеттігі баса айтылған.
Алға қойылып отырған негізгі талаптар-Қазақстан білім беру жүйесінің бүкіләлемдік білім беру кеңістігіне торлық енуінің алғашқы ұлттық даму стратегиясын жасап, моделін құру.
Бұл талаптардың жүзеге асырылу бағытындағы жұмысты үздіксіз білім берудің алғашқы сатысы-оқушының білімге деген құштарлығын арттырудан, ұлтымызға тән қасиеттер бойына сіңген шәкіртті жаңа заман талаптарына сай оқытып-тәрбиелеу негізгі міндетке айналып отыр.
Қазіргі таңда мектептегі білім беруді қайта құрудың негізгі бағыты оқытудың дамытушылық функциясын басымдылыққа алу болып табылады. ЖББ мектептің жоғарғы сынып оқушыларына арналған «Функция қасиеттері, теңдеулер мен теңсіздіктерді шешу» тақырыбы оқушылардың есеп шығаруда өз білімдерін көтеру, тереңдету, тиімді жолдарын таба білу және білімдерін бекіту мақсатында есептердің шығару тәсілдерін үйренуде, іскерлік-дағдыларын қалыптастыруда маңызы зор. Математиканың тарихи даму барысында әр қырына, түрінше шешімін тауып отырған ең басты мәселелердің бірі-сан ұғымын дамыту болды. Сан ұғымын кеңейту мәселесі алгебра ғылымының өз алдында бөлініп дербес даму жолына түсуін күрт жеделдетті, шешуі болатын теңдеулер класын көбейтті, қолданыстағы сандар арсеналын байытуды, кеңейтуді талап етті. Алгебра иррационалдықтың, яғни иррационал сандардың рационал сандармен тең енгізілуі осы қажеттіліктің көрінісі екені белгілі.
Теңсіздіктерді шешу қиын есептерді шешуді жеңілдетеді. Есепті шешу үшін есептің шарты баяндалған математикалық тілді математикалық модель-өрнекті құру үшін белгісізді х, у, z деп белгілеп, шартта баяндалған барлық жағдайды еске алып өрнек теңдеу құрамыз. Ары қарай осы өрнектен белгісізді табу теңдеуді шешу болып табылады.
Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады. Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.
Бұл курстық жұмыс алгебра курсында қарастырылатын квадрат теңсіздіктерге және оларды шешу жолдарының әр түрлі әдістеріне негізделініп отыр.
«Квадрат теңсіздіктер» мектептегі алгебра курсының маңызды тақырыптарының бірі. Көптеген табиғи үдірістер мен құбылыстар, с. с. мазмұнды есептердің шығарылуы квадрат теңсіздітерді шешуге келіп тіреледі. Теңсіздіктерді шешу, функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін, өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді табу есептерін шығару және т. б. жағдайларда квадрат теңсіздітерді шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық, көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада, геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат теңдеулерге келтіріледі.
І. Теңсіздік түрлері
Теңсіздіктер- сандарды салыстыруға арналған математиканың бір саласы
Теңсіздік белгілері
- ‘’>’’ Егер a>b болса, онда a саны артық b санынан артық
- ‘’< ‘’ Егер a<b болса, онда a саны b санынан кіші
- ‘’≥’’ Егер a ≥ b болса, онда a саны b санынан үлкен немесе оған тең
- ‘’≤’’ Егер a ≤ b болса, онда a саны b санынан кіші немесе оған тең
- ‘’≠’’ Егер a ≠ b болса, онда a саны b санына тең емес
Теңсіздік түрлері
- Логарифмдік теңсіздіктер
- Көрсеткіштік теңсіздіктер
- Квадраттық теңсіздіктер
- Жоғарғы дәрежелі теңсіздіктер
a f(x) ≥ a g(x) теңсіздігі көрсеткіштік теңсіздік деп аталады.
Бұл теңсіздік мына теңсіздіктерге эквивалентті:
1) . a > 1 болса онда f(x) ≥ g(x)
2) . 1> a > 0 болса онда f(x) ≤ g(x)
Мысалы (бірінші мысал) 3 2x ≥ 3 x+1 теңсіздігін шешейік:
3 2x ≥ 3 x+1
3>1
2x ≥ x+1 (сызықты теңсіздіктер)
2x-x ≥ 1
x ≥ 1
Жауабы: x ≥ 1.
Екінші мысал.
(0, 5) 4x ≤ (0, 5) x+6 теңсіздігін шешейік:
(0, 5) 4x ≤ (0, 5) x+6
1 > 0, 5 > 0
4x ≥ x+6
4x-x ≥ 6
3x ≥ 6
x ≥ 6/3
x ≥ 2
Жауабы: x ≥ 2.
Жаттығулар.
Мына көрсеткіштік теңсіздіктерді шешіңіз:
a) . 5 4x ≥ 5 x+9 b) . (0, 3) 5 ≥ (0, 3) x+3 c) . 5 2y ≥ 25 y-1
Ізделінетің белгісізі тек белгілі бір санның (сандардың) дәрежесіне (дәрежелеріне) ғана еңетің теңдеулерді көрсеткіштік теңдеулер деп атайды.
Мысалы 4 x -2 x+1 +1=0 теңдеуі көрсеткіштік теңдеуі болады, өйткені мұнда ізделінетің белгісіз x саны 4 және 2 сандарының дәрежелеріне еңеді.
Бұл теңдеуді шешу үшін дәреженің қасиеттерін пайдаланамыз:
4 x -2 x+1 +1=0
(2 2 ) x -2 1 ·2 x +1=0
2 2x - 2·2 x +1=0
(2 x -1) 2 =0
2 x -1=0
2 x =1 x=0 Жауабы: x=0 .
Кейбір тригонометрикалық теңдеулерді шешу үшін қосымша айнымалыны еңгізу қажет болады.
3 2x - 4·3 x +3=0
3 x =t
t 2 -4·t+3=0
t 1 =1
t 2 =3
3 x =1
x 1 =0
3 x =3
x 2 =1
Жауабы: x 1 =0 , x 2 =1 .
- Теңсіздіктің шешімдер жиыны.
- Теңсіздік D < 0 D = 0 D > 0ах2 + вх +с > 0 (-∞ ; + ∞ ) (-∞ ; +∞ ) (-∞ ; х1 ) U (х2 ; + ∞ )
2 ах2 + вх +с < 0 Бос жиын Бос жиын (х1 ; х2)
3 - ах2 + вх +с > 0 Бос жиын Бос жиын (х1 ; х2)
4 - ах2 + вх +с < 0 (-∞ ; + ∞ ) (-∞ ; +∞ ) (-∞ ; х1 ) U (х2 ; + ∞ )
Мысалдар: 1) х2 < 16 х2 = 16
x 1., 2 = ± √16 = ± 4,
x1= -4, x2 = 4. Жауабы: (-4 ; 4 ) .
2-мысал . ( 2х 2 - 7 ) -4 < 0
( 2х 2 - 7 ) -4 = 0
( 2х 2 - 7 ) = 4
( 2х 2 - 7 ) = ( ± 2 ) 2
2х - 7 = -2 2x - 7 = 2
2x = 7-2 2x = 7+2
2x = 5 x1 = 2, 5 2x = 9, x2 = 4, 5
Жауабы: (2, 5 ; 4, 5 ) .
2-мысал. ( х - 9 ) 2 + 3 > 0 Жауабы: (-∞ ; + ∞ )
4-мысал. ( х - 2 ) ( 2х + 5 ) ≤ 0 x - 2 = 0 x 1 = 2
2x + 5 =0 2x = -5 x2 = -2, 5 .
Жауабы: [ -2, 5 ; 2 ] .
5-мысал. 2х2 -3х -5 ≥ 0 2 + 3 - 5 = 0 х1 = -1, x2 = 5/2 = 2, 5.
Жауабы: (-∞ ; -1 ] U [ 2, 5 ; + ∞ )
Теңсіздіктерді дәлелдеу тәсілдері
- Теңсіздікті анықтама бойынша дәлелдеу
- Теңсіздікті кері жору тәсілімен дәлелдеу
- Теңсіздікті тірек-теңсіздіктер тәсілімен дәлелдеу
- Теңсіздіктерді жуықтап бағалау тәсілімен дәлелдеу
- Теңсіздікті математикалық индукция тәсілімен дәлелдеу
ІІ. Квадраттық теңсіздік
2. 1. Квадраттық теңсіздік анықтамасы
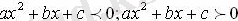 ( мұндағы х - айнымалы; а. в, с -сандар,
( мұндағы х - айнымалы; а. в, с -сандар,
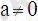 ) түріндегі теңсіздіктер квадраттық теңсіздіктер деп аталады. Квадраттық теңсіздіктің шешімі деп квадраттық теңсіздікті қанағаттандыратын айнымалының барлық мәндерінің жиынын айтады. Оны шешудің үш түрлі тәсілін қарастырайық:
) түріндегі теңсіздіктер квадраттық теңсіздіктер деп аталады. Квадраттық теңсіздіктің шешімі деп квадраттық теңсіздікті қанағаттандыратын айнымалының барлық мәндерінің жиынын айтады. Оны шешудің үш түрлі тәсілін қарастырайық:
а) квадрат үшмүшені көбейткіштерге жіктеп, әрбір көбейткіштің нөлге айналатын нүктелерін анықтап, осы нүктелер көмегімен сан осін бөліктерге бөліп және осы бөліктердің әрқайсысында көбейткіштердің таңбалары арқылы квадрат үшмүшенің таңбасын анықтау. Бұл тәсіл - аралықтар (интервалдар) әдісі деп аталады.
Ә) квадрат үшмүшені көбейткіштерге жіктеп, көбейтіндінің оң (не теріс) болуы заңдылықтарын қолдану
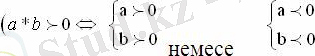
Б) квадрат үшмүше графигінің абсциссалар осіне қатысты орналасуын анықтап, оның оң және теріс бөліктерін көрнекі деңгейде анықтау.
Квадрат теңсіздіктерді шешу үшін:
I жағдай. 1) а>0 және D>0.
Квадраттық функцияның графиктері абсцисса осін х 1 ; х 2 нүктелерде қияды, парабола тармақтары жоғары бағытталған.
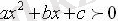 функциясы үшін түбірлерінің «сыртындағы» мәндер
функциясы үшін түбірлерінің «сыртындағы» мәндер
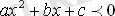 функциясы үшін түбірлерінің «арасындағы» мәндер алынады.
функциясы үшін түбірлерінің «арасындағы» мәндер алынады.
2) а<0 және D>0. Бұл жағдайда парабола тармақтары төмен бағытталады, жауап:
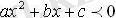 теңсіздігі үшін х<х
1
және х>х
2
;
теңсіздігі үшін х<х
1
және х>х
2
;
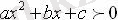 теңсіздігі үшін х
1
< х < х
2
болады.
теңсіздігі үшін х
1
< х < х
2
болады.
I I жағдай. 1) а>0 және D=0.
Квадрат үшмүшенің екі бірдей түбірі бар:
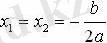
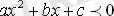 теңсіздігі үшін шешімі болмайды ;
теңсіздігі үшін шешімі болмайды ;
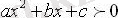 теңсіздігі үшін
теңсіздігі үшін
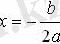 мәнінен басқа кез-келген мән болады.
мәнінен басқа кез-келген мән болады.
2) а< 0 және D=0.
Бұл жағдайда парабола абсцисса осін
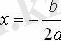 нүктесінде жанайды, Ох осінен тармақтары төмен бағытталады, жауап:
нүктесінде жанайды, Ох осінен тармақтары төмен бағытталады, жауап:
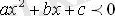 теңсіздігі үшін
теңсіздігі үшін
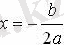 мәнінен басқа кез-келген мән болады ;
мәнінен басқа кез-келген мән болады ;
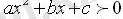 теңсіздігі үшін шешімі болмайды.
теңсіздігі үшін шешімі болмайды.
III Жағдай. 1) а>0 және D < 0.
Бұл жағдайда квадрат үшмүшенің нақты түбірлері жоқ және график Ох осінен жоғары орналасқан, яғни абсцисса осімен қиылыспайды. Сондықтан
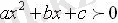 теңсіздігі х- тің кез-келген мәнінде орындалады, ал
теңсіздігі х- тің кез-келген мәнінде орындалады, ал
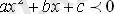 теңсіздігінің шешімі болмайды.
теңсіздігінің шешімі болмайды.
2) а < 0 және D < 0. Квадрат үшмүшенің нақты түбірлері жоқ және график Ох осінен төмен орналасқан, яғни абсцисса осімен қиылыспайды .
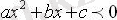 теңсіздігі х- тің кез-келген мәнінде орындалады, ал
теңсіздігі х- тің кез-келген мәнінде орындалады, ал
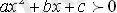 теңсіздігінің шешімі болмайды.
теңсіздігінің шешімі болмайды.
Тенсиздик угымы
a санының b санынан үлкен (кіші) екендігін көрсету үшін a>b (a<b) жазамыз.
Мысалдар.
5>2, 3>0, 7<9, 100<150, -2>-3
Үлкен >, кіші < белгілерімен қатар үлкен не тең ≥ және кіші не тең ≤ деген белгілері қолданылады.
a ≥ b (a ≤ b) деген белгілеуі a санының b санынан үлкен (кіші) не оған тең болуын көрсетеді.
>, <, ≥, ≤ белгілері теңсіздік белгілері деп аталады.
Өрнектің сол және оң жағы теңсіздік белгісімен байланысса онда бұндай өрнекті теңсіздік деп атаймыз.
Теңсіздіктердің қасиеттері:
1) . a > b, c > d болса онда a+c > c+d .
Мысалы 7 > 5, 3 > 2 соңдықтан 7+3 > 5+2.
2) . a ≥ b, c ≥ d болса онда a+c ≥ c+d .
3) . a > b болса онда - a < -c .
Мысалы 2>1, -2<-1.
4) . a ≥ b болса онда - a ≤ -c .
5) . a > b болсын, k саны оң болса онда k · a > k · b , k саны теріс болса онда k · a < k · b.
Мысалы 3 > 2, 4 · 3 > 4 · 2, -4 · 3 < -4 · 2.
6) . a ≥ b болсын, k саны оң болса онда k · a ≥ k · b , k саны теріс болса онда k · a ≤ k · b.
Келесі сабақтарда белгісізі бар теңсіздіктерді шешу жолдарын қарастырамыз. Мысалы 2x+1>3 типті теңсіздіктерін.
2. 2. Квадрат теңсіздікті шешу әдістері
Көп жағдайда квадрат теңсіздіктерді шешу үшін интервалдар әдісін қолданған тиімді.
ax2 +bx+c>0 (а=0) квадрат теңсіздігі берілсін. Бұл теңсіздікті интервалдар әдісімен шешу үшін, алдымен, у =ax2 +bx+c функциясы графигінің Ох осімен қиылысу нүктелерінің абсциссаларын, яғни функцияның нөлдерін табу керек, теңдеу түбірлерін табу керек
1 - мысал. 2х2+9х+4>0 теңіздігін шешейік
Шешуі: у=2х2+9х+4 функциясының нөлдерін табайық.
2х2+9х+4=0
D=92 - 4*2*4=81 - 32=49
х1= = =4; х1= = =- 0, 5
+ -- +
- 4 - 0, 5
Жауабы: (-∞; - 4) (- 0, 5; + ∞)
Теңсіздіктерді интервелдар әдісімен шешу үшін келесі алгоритм қолданылады:
Берілген теңсіздікті Р(х) 0, Р(х) ≤0, Р(х) ≥0 түрлерінің біріне келтіреміз;
Теңсіздіктің сол жағын нөлге теңестіріп, шыққан теңдеуді шешеміз, яғни сәйкес функцияның нөлдерін табамыз;
Теңдеудің түбірлерінің мәнін сан осіне белгілеп, сан осін интервалдарға бөлеміз;
Интервалдың кез - келген біреуінде функцияның таңбасын анықтап, осы интервалға анықталған таңбаны қоямыз;
Теңдеудің түбірі қайталанебаған немесе тақ рет қайталанған жағдайда қалған интервалдардағы таңбаларды кезекпен қоямыз; ал егер жұп рет қайталанса, осы түбірдің екі жағындағы интервалдардың таңбаларын бірдей етіп аламыз;
Таңбасы теңсіздік таңбасына сәйкес интервалдарды жауап ретінде аламыз.
2- мысал:
(х+3) /(х^2 (х - 4) ) ≥0 теңсіздігін шешейік
Шешуі: Алгоритм бойынша бірден у=х², у=х+3, у=х - 4теңдеулерінің түбірін
табамыз. Сонда теңдеулерге сәйкес х1=х2=0, х3=- 3 және х=4 түбірлері шығады. - 3, 0, 4 сандарын сан түзуінде белгілесек, төрт интервал аламыз. Интервалдардың біреуіндегі таңбаны анықтау үшін, мысалы, төртінші интервалдан 5 санын алып, берілген теңсіздіктің сол жағындағы өрнекке қойып, мәнін есептеймізтөртінші интервалтаңбасы «+» таңбасын қоямыз. Енді қалған интервалдардағы таңбаларды кезекпен қойып шығу үшін х=0 түбірі екі рет . Сонда интервалдар таңбасы төмендегідей болады.
+ - +
- 3 0 4
Интервалдардағы таңбаларды берілген теңсіздік таңбасымен салыстырып, берілген теңсіздіктің жауабы «+» таңбасы бар интервалдар екенін анықтаймыз. Яғни, теңсіздік х≤- 3 және х>4 болғанда орындалады.
Жауабы: (-∞; - 3] (4; +∞)
- - мысал:
D <0 теңсіздігін шешейік
Шешуі: Берілген теңдеулердің түбірін табамыз. Сонда бірінші теңдеудің түбірлері х1=- 6, х2=3, екінші теңдеудің түбірлері х1; 2=-, үшінші теңдеудің түбірлері х1=2, х2=3, төртінші теңдеудің түбірі болмайды, өйткені D=- 104<0
Сан түзуінде - 6, 3, -, 2 нүктелерін белгілеп, бес интервал аламыз. х=0 нүктесі тиісті болатын үшінші интервалдың таңбасын анықтасақ, теріс сан шығады.
Демек, интервалдар таңбасы төмендегі суреттегідей болады. Бұл жерде х1=-, және х=3 түбірлері екі рет қайталанатыны ескерілген
Енді берілген теңсіздіктің таңбасын интервалдар таңбасымен салыстырып, жауап ретінде екінші және үшінші интервалдарды аламыз
+ - + +
- 6 - 2 3
Жауабы: (- 6; - ) (-; 2)
Есептер шығару.
1. (х - 1) (х + 4) ≥0, x - 1 =0, x+ 4 =0, x=1, x=- 4
+ - +- 4 1
жауабы. ├] -∞; - 4] ∪[1; +∞┤[
(х+2) (х - 3) <0 x+2=0, x - 3=0, x=- 2, x=3
+ - + жауабы. (- 2; 3) - 2 3
(х - 5) (х - 1, 5) 0, x=0, x=2
+ - + жауабы. (-∞; 0) ∪(2; +∞) 0 2
5х(3+x) (x - 9) 0, х=2, х≠- 2
+ - + жауабы. (-∞; - 2) ∪(2; +∞) - 2 2
Функцияның графигінің көмегімен кейбір теңсіздіктерді шешуге болады.
х²-х-6>0; х²-х-6≥0; х²-х-6≤0; х²-х-6<0 теңсіздіктерді шешіп көрелік.
Мысалы, осы графиктің көмегімен х²-х-6>0 теңсіздігін қалай шешуге болады? График бойынша функцияның оң мәндерін анықтаймыз, яғни график Ох осінен х<3 және х>-2 болғанда жоғары орналасқан Жауап графиктен көрсетіледі. Ал 3 және -2 теңсіздіктің шешімі бола ала ма? Теңсіздік қатаң болғандықтан, шешімі бола алмайды.
Осылайша қалған теңсіздікті шешу қарастырылады. Қазір біз шешкен теңсіздіктер квадрат теңсіздіктер деп аталады.
Анықтама: ах²+bх+с>0, ах²+bх+с<0, ах²+bх+с≥0, ах²+bх+с≥0 түріндегі теңсіздіктер квадрат теңсіздіктер деп аталады. Мұндағы а≠0.
Біз сіздермен квадрат теңсіздікті шешудің графиктік тәсілін таптық.
Квадрат теңсіздікті шешу үшін, бізге квадрат функцияның графигін салу қажет. Ал бұл оңай емес. Мүмкін есеп шығару жолын оңтайландыруға болатын шығар? Теңсіздікті шешу үшін графикті дәл салу қажет пе? Жоқ, бізге тек графиктің Ох осін қиятын нүктелері мен параболаның тармақтарының бағыты ғана маңызды.
Есептер шығарып көрелік.
№1. (х - 1) (х + 4) ≥0 3-топ (x-8) (x+11) <0
x -1 =0 x+ 4 =0 x-8=0 x+11=0
x=1 x=-4 х=8 х=-11
Жауабы: (-∞; -4] [1; +∞) Жауабы: (-11; 8)
№2. (х+2) (х-3) <0 4-топ (х+7) (3- х ) < 0
x+2=0 x-3=0 x+7=0 3-x=0
x=-2 x=3 х=-7 х=3
Жауабы: (-2; 3) Жауабы: (-∞; -7) (3; +∞)
В деңгейіндегі есептер.
1. -2х2 - 5х +3 0 3. x(2-x) >0
D=25+24=49; x1=-3; x2=0, 5 x=0 2-x=0
-2х2 - 5х +3=-2(x+3) (x-0, 5 ) x=2
Жауабы: (-∞; -3] [0, 5; +∞) Жауабы: (0; 2)
2. -x2 - 2x + 8>0 4. -2х2-х+6
D=4+32=36 D= 1+48=49
x=-4 x=2 x1=-2 x2= 1, 5
-x2 - 2x + 8= -(x+4) (x - 2) >0 -2х2-х+6х-2=-2(x+2) (x-1, 5)
Жауабы: (-4; 2) Жауабы: [-2; 1, 5]
1. 5х(3+x) (x - 9) <0 2. 5x2-2x-3 0
5x=0 3+x=0 x-9=0 D=4+ 60 = 64; х1= 1 x2= -0, 6
x=0 x=-3 x=9 5x2-2x-3 =5(x -1) (x+0, 6)
Жауабы: (-∞; -3) (0; 9) Жауабы: [-0, 6; 1]
3. 3x2 -7x +2 <0 4. - 2x2 -5x +3 0
D=49 - 24 = 25; х1= 2 x2= D= 25 + 24 = 49; х1= -3 х1=0, 5
3x2 -7x +2=3(х-2) (х- ) 0 - 2x2 -5x +3 =- 2(x+3) (x-0, 5)
Жауабы: ( ; 2) Жауабы: [-3; 0, 5]
2. 3. Квадраттық функция. Квадраттық функция деп мына түрде беруге болатын функцияны айтады
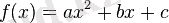 , мұнда
, мұнда
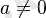
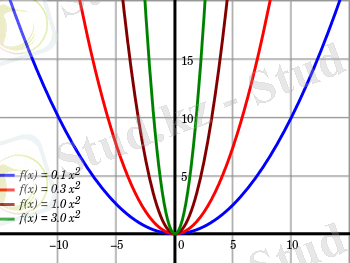
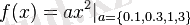
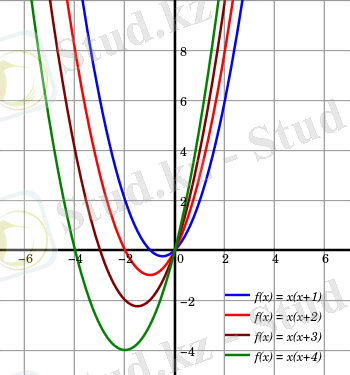
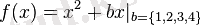
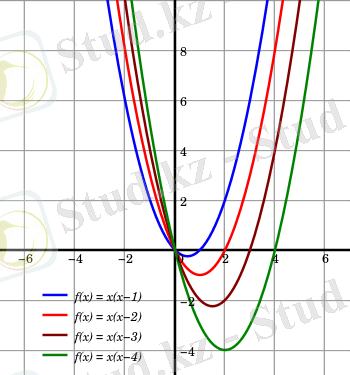
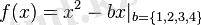
Квадраттық функцияның графигі парабола деп аталады.
Жалпы түрде квадраттық функцияның теңдеуі мына түрде жазылады:
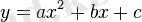 . Парабола төбесінің координаттары:
. Парабола төбесінің координаттары:
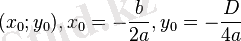 .
.
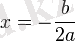 түзуі квадраттық функция графигінің симметрия осі деп аталады.
түзуі квадраттық функция графигінің симметрия осі деп аталады.
Егер a<0 болса парабола төмен тармақталған болады, a>0 болғанда - жоғары тармақталған.
Квадраттық функцияның қасиеттері дискриминанттың мәніне байланысты болады. Дискриминант мына формула бойынша есептеледі
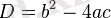
- болғандағы квадраттық функцияның қасиеттері (Осы түспенболғандағы қасиеттері көрсетілген. ) :

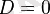

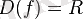
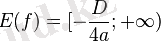
![E(f)=(-\mathcal{1};-\frac{D}{4a}]](https://kz-rkd-img.s3.studkz.pro/26396/image39.webp)
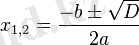
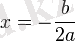

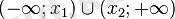
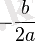 нүктелерден басқа барлық жерде
нүктелерден басқа барлық жерде
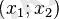
![(-\mathcal{1};-\frac{b}{2a}]~](https://kz-rkd-img.s3.studkz.pro/26396/image45.webp)
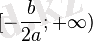
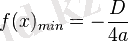
Еркін құлап жатқан дене биіктігінің уақытқа тәуелділігі.
- Фигура ауданының оның сызықтық өлшемдеріне тәуелділігі (мысалы, дөңгелек ауданының радиусқа тәуелділігі) .
Көп айнымалы жағдайына жалпылау екінші ретті беттер болып табылады. Ондай теңдеудің жалпы түрін мына түрде жазуға болады:
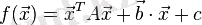
Бұл жерде:
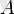 - квадрат түрдегі матрица,
- квадрат түрдегі матрица,
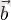 - тұрақты,
- тұрақты,
 - константа. Бұл жағдайда да функцияның қасиеттері (бірінші ретті жағдайына ұқсас) теңдеудің негізгі коэфиценті
- константа. Бұл жағдайда да функцияның қасиеттері (бірінші ретті жағдайына ұқсас) теңдеудің негізгі коэфиценті
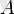 матрицасымен анықталады.
матрицасымен анықталады.
ІІІ. Квадрат теңдеулер
ax + ax 2 + c = 0, a ≠ 0 түріндегі теңдеулерді квадраттық теңдеу деп атайды. Мұндағы х-айнымалы шама, а, в, с нақты сандар, әрі а-екінші дәрежелі мүшенің коэффициенті, в-бірінші дәрежелі мүшенің коэффициенті, с-бос мүше. ax 2 + bx + c = 0 квадраттық теңдеуінде коэффициенттерінің бірі - в не с немесе в мен с- ның екеуі де нөлге тең болса, ондай теңдеулерді толымсыз квадраттық теңдеу деп атайды.
1) в = c = 0 болса, онда ax 2 = 0; шешуі: х = 0
2) c = 0, b ≠ 0 болса, онда ax 2 + bx = 0; шешуі : x (ax + b) = 0; х = 0; x= - b/a
3) с ≠ 0, b = 0 болса, онда ax
2
+ c = 0; шешуі : x
2
=; егер -c/a ≥ 0 болғанда
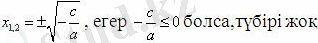
Мысал: Ауданы 6 м2 тіктөртбұрыш пішінді жер телімін қоршау керек болсын.
Жер телімінің бір қабырғасы (ұзындығы) қоршау бар жақтан өтеді. Егер қоршауға
арналған материалдың ұзындығы 8 м ғана болса, онда тіктөртбұрышты жер
телімінің ені қандай болу керек?
Шешуі: Ені - х м.
Ұзындығы - (8-2х) м 2
х*(8-2х) = 6
2х-8х+6 =0
х 2 -4х+3 =0
х 2= 4х-3ху
х 2 , у 4х-3 болатын екі функция қарастырылады.
Демек, теңдеудің екі шешімі бар. Есептің шартын х 1 мәні ғана
қанағаттандырады. Сонымен, жер телімінің ені 1м, ал ұзындығы сәйкесінше 6м.
Есеп шығару барысында жаңа х 2 -4х+3 0 теңдеуі қарастырылды.
Анықтама: ах 2 +вх+с 0 =(1)
түрінде берілген теңдеу квадрат теңдеу деп аталады.
Мұндағы а, в, с-нақты сандар және а 0, ал х-айнымалы. (1) теңдеудегі а-
бірінші коэффициент, в-екінші коэффициент, с-бос мүше.
Егер (1) теңдеудегі в 0 және с 0 болса, онда ол теңдеу толық квадрат
теңдеу деп аталады.
Мысалы: х 2 -2х-1= 0, 3х 2 -8х+5= 0, 2, 1х 2 +102, 3х+0, 8 =0 толық квадрат
теңдеулер. в немесе с, немесе в мен с нөлге тең болатын дербес жағдайлардағы квадраттеңдеу толымсыз квадрат теңдеу деп аталады.
Толымсыз квадрат теңдеулер былай жазылады:
ах 2 +вх= 0 (мұндағы с 0) ;
ах 2 +с= 0 (мұндағы в 0) ;
ах 2 =0 (мұндағы в 0, с 0) .
Егер толық квадрат теңдеудегі бірінші коэффициент 1-ге тең (а 1) болса, ондаол келтірілген квадрат теңдеу деп аталады.
Келтірілген квадрат теңдеу
х 2 +рх+q =0
түрінде жазылады. Мұндағы р жәнеq -кез келген нақты сандар. Енді толымсыз квадрат теңдеулердің шығарылуын қарастырайық.
ах 2 +вх= 0, мұндағы а 0
шешу жолын келтірейік.
х(ах+в) 0
теңдеуін аламыз.
х 1 =0 және х 2 =- болатын екі түбірі болады.
1-мысал:
6х 2 -3х= 0 теңдеуін шешейік.
х(6х-3) = 0
х 1 =0, 6х-3 =0 х 2 = = ; Жауабы: 0; .
Енді ах 2 +с= 0, мұндағы а 0≠ (4) толымсыз квадрат теңдеуінің шешімін
қарастырайық. Бұл теңдеудің екі жағын а-ға бөлеміз.
х 2 =- - (5)
теңдеуін аламыз.
1-жағдай: а және в сандарының таңбалары бірдей, онда оң сан, - теріс сан
болады. х 2 =0 екені белгілі, сондықтан ол теріс санға тең болуы мүмкін емес.
Теңдеудің шешімі болмайды.
2-жағдай: с= 0 болсын. х 2 =0 теңдеуіне көшеді. Теңдеудің бір ғана х =0 шешімі
бар.
3-жағдай: а және с сандарының таңбалары қарама-қарсы (яғни, біреуі оң,
екіншісі теріс сан) . Бұл жағдайда х 2 =- теңдеуінің х 1, 2 ± екі түбірі болады.
2- мысал: 4х 2 -9= 0 теңдеуін шешейік. 4х 2 = 9
х 2 = ; х1= ; х2=- . Жауабы: ; - . ;
3-мысал: 5х 2 -8=7х 2 -8 теңдеуін шешейік.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz