Вектор ұғымының теориялық негіздері және кеңістіктегі математикалық әдістемесі


Жоспар
Кіріспе . . . 2
І. Вектор ұғымының теориялық сипатталуы . . . 3
1. 1. Вектор ұғымы және оның шығу тарихы . . . 3
1. 2. Векторларға амалдар қолдану . . . 5
1. 3. Векторларды жіктеу тәсілдері . . . 12
ІІ. Кеңістіктегі вектордың математикалық әдістемесі . . . 14
2. 1. Кеңістіктегі векторлар . . . 14
2. 2. Векторлардың скаляр көбейтіндісі оның қасиеттері . . . 18
2. 3. Векторлардың аралас көбейтіндісі оның қасиеттері . . . 22
Қорытынды . . . 29
Пайдаланылған әдебиеттер тізімі . . . 30
Кіріспе.
Қоғамдағы қазіргі кездегі қайта құрулар, экономианы дамытудағы жаңа стратегиялық бағдарлар, қоғамның ашықтығы оның жедел ақпараттануы мен қарқынды дамуы білім беруге қойылатын талаптарды түбегейлі өзгертті.
Әлемнің жетекші елдерінің көпшілігінің білім беру, білім берудің мақсатын, мазмұны мен технлогияларын оның нәтижесіне қарап бағалайтын болды.
Жас ұрпақты жан-жақты жетілген, ақыл парасаты, өресі биік, өз отанын сүйетін азамат етіп тәрбиелеудегі басты тұлға -ұстаз. Қазіргі таңда жемісті еңбекпен, шығармашылық ізденіс арқылы ғана реалды жаңару жолына шыға аламыз.
Математиканы оқытудағы негізгі міндет-математикалық білік, білім жүйелерін нақты және сапалы меңгеруді қамтамасыз ету қабілеттерін дамыту мен анықтау.
Тәуелсіз Қазақстанымыздың экономикасы өркендеп, өндіріс орындарының жандануына байланысты математика саласының ғылымдарына, білікті мамандарына сұраныс қазіргі кезде күрт артып отыр.
Оқушыларға мектепте оқытылатын математика салаларын, соның ішінде, техникалық ғылымдардың негізі болып табылатын векторлар ұғымын неғұрлым тереңірек білгізіп, меңгерту керек.
І. Вектор ұғымының теориялық сипатталуы.
1. 1. Вектор ұғымы және оның шығу тарихы.
Қазіргі заман математикасының негізгі де ілгерлі ұғымдарының бірі -векторлық кеңістік ұғымы. Бұл ұғым математиканың сызықтық алгебра, сызықтық программалау, функционалдық анализ және физиканың толып жатқан салаларында қолданылады.
Векторлық аппарат қазіргі заман математикасында қолданумен шектелмей, жоғары оқу орындарында оқытылатын техникалық матеатика пәндерінің оқулықтарында лайықты орын алды. Векторлық аппараттың атқаратын рөлінің маңызы соншалық-аталмыш курстар векторлардың өздеріне қажетті тараулардың толығымен қамтиды.
Қазіргі кезде экономикалық есептердің көпшілігі векторлық аппарат көмегімен шешіледі. Компьютерді дефференциялдық геометрия, аналитикалық геометрия, математикалық физика, теориялық физика векторлар негізінде баяндалады.
Векторлар математика мектептерде оқытыла бастағанына ширек ғасырдан астам уақыт болды. Абстрактылығы жоғары векторларды оқушыларға саналы да терең меңгерту үшін, олардың векторларды оқып білуге деген ынтасын арттыру үшін тарихи мағлұматтар бере отырудың маңызды екені сөзсіз.
Техника ғылымдарының қауырт дамуына байланысты он сегізінші ғасырдың өзінде ақ есептеу аппаратын жетілдірудің қажет екендігі байқалды. Бұрыннан қолданылып келген есептеу түрлері ендігі жерде қажеттілікті қанағаттандыра алмайтын болып шықты. Теориялық физиканың жедел де аса күшті қарқынмен дамуына байланысты он тоғызыншы ғасырдың басында математикалық аппаратты жетілдіруге деген талап күшейе түсті. Есептеудің талапқа сай жаңа түрін іздестіру қажет болды. Нәтижесінде он тоғызыншы ғасырдың екінші жартысында векторлық есептеулер дүниеге келді де, үлкен қарқынмен тез дамыды және математиканың құрамдас бір бөлігі болып қалыптасты
Векторлық есептеулерді жасауға көптеген елдердің толып жатқан ғылым математиктері мен физика-механиктері, инженер-техниктері қыруар үлес қосты. Векторлық есептеулердің жасы жас болғанымен бастау көзі сонау ерте заманда өмір сүрген данышпан Аристотельдің «Механикалық проблемалар» атт еңбегінде табылды. Аристотельдің қозғалыстарды қосуға параллелограмм ережесін қолданғандығы, векторлардың геометриялық қосындысын табудың қазіргі біз қолданып жүрген түріне өте жақын келгендігі анық байқалды. ХҮІ -ғасырда Аристотельдің «қозғалыстар параллелогамы» қайтадан жанданды. Галилео Галелей күш және оның денені қозғайтын құраушының арасындағы метрикалық байланысты зерттеді. Оның еңбектеріне қарап,
Галелейдің «тең әсерлі күш», «қорытқы жылдамдық», ұғымдарына өте жақын,
қапталдас келгенің көруге болады. Ағылшын математигі, әрі физигі атақты Исаак Ньютон қозғалыстарды қосуға алғаш рет «параллелограмм ережесін пайдаланды. Неміс математигі Готфрид Вильгельм Лейбниц «геометриялық есептеулер» идеясын берді, оны әрі қарай дамытпады.
Механикадағы векторлық алгебраның негізін қалаушы Джон Валлис механикаға геометриялық аппарат жасап беруг жаңа әрі аса ірі қадам жасады. Ол екі, үш күштің тең әсерлі және қорытқы күшін табуға қорытқы жылдамдықты табуға қлданылатын параллелграмм ережесін ғылымға алғаш енгізген Джон Валлис болды. Ол механикада вектрлық алгебраның негізін қалаған оқымысты болды.
Векторлық есептеулердің негізін салушылар Ирландия математигі әрі астрномы Уильям Тамильтн және неміс математигі және неміс математигі Герман Грассман деп айтылып жүр.
Д. Валлис, Л. Карно, Сен-Венан, Резаль бұлар векторлық алгебра мен векторлық анализдің ұғымдарын ғылымға еңгізді, механикаға қажетті геометриялық аппарат жасау жолында жемісті еңбек етті.
Вектолық есептеулерді жасауға үлес қосқандардың ең көрнекті дегендеріне қысқаша тоқталдық. Ғылымның бұл саласын дамытуға, практикада қолдануға бұладан басқа да үлес қосқандар аз болған жоқ. Солардың қатарында:К. Бессель, К. Гаусс, Г. Белловитис, К. Максвель, Д. Гиббс, Л. Лоуренс, А. Мебиус, Арган, Хивисоид т. б атауға болады.
Векторлық есептеуді және олардың тамаша қолдануларын дамытуға И. И. Сомовтан басқа да орыс және Кеңес ғылымдарының қосқан үлкен үлес болды. Осы тұрғыда атақты математик -Санк-Петербург академиясының академигі М. В. Остроградскийді және П. А. Котельников, А. Л. Фридман, Н. Е. Кочин, Я. И. Френкель. П. А. Широков, Д. И. Зейлиегер сияқтыларды атаған жөн.
1. 2. Векторларға амалдар қолдану
Вектор деп бағытталған кесіндіні атаймыз. Яғни AB вектордың A басы мен B ұшы бар болады:
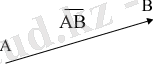
Мысалы.
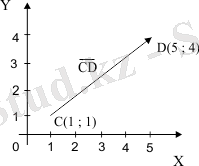
Вектордың басы мен ұшының арақашықтығы оның (вектордың) ұзындығы немесе абсолюттік шамасы деп аталады.
Мысалы жоғарыдағы CD векторының CD ұзындығы:
CD=
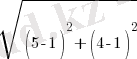
CD=
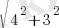
CD=
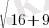
CD=

CD=5
Егер вектордың басы мен ұшы бір нүктеде орналасса онда бұндай векторды нөлдік вектор деп атайды. Өйткені бұндай вектордың ұзындығы нөлге тең.
Вектордың координаттары деп оның (вектордың) ұшының және басының сәйкесінше координаттарының айырмасын атаймыз.
Яғни AB векторының басы A(x 1 , y 1 ) нүктесі ал ұшы B(x 2 , y 2 ) нүктесі болса онда AB векторының координаттары (x 2 -x 1 , y 2 -y 1 ) болады.
Мысалы жоғарыдағы CD векторының координаттары (5-1; 4-1) =(4; 3) .
Геометрияда сәйкесінше координаттары бірдей векторларды бірдей векторлар деп санайды. Соңдықтан векторларды a, b, c, … деп бір ғана әріппен белгілейміз. a векторының координаттарын (a x , a y ) деп белгілейміз. Ал a векторының өзін кейде {a x , a y } деп те белгілейміз.
Бағытталған кесінді
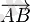 деп
деп
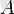 - “бас нүктесінен” бастап екінші
- “бас нүктесінен” бастап екінші
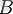 - “соңғы”нүктесіне дейінгі түзу бойындағы нүктелер жиыны.
- “соңғы”нүктесіне дейінгі түзу бойындағы нүктелер жиыны.
Жәй мағынасына сәйкес вектор деп бағытталғын кесінді деп түсінуге болады, ал басқа жағдайларда әртүрлі векторлар - белгілі бір эквиваленттік қатынасы бойынша әртүрлі бағытталған кесінділер эквивалентті класстары болып табылады. Бұл қатынасы әртүрлі болуы мүмкін: ол векторлардың түрін анықтайды (“еркін”, “тұрақты” т. б. ) . Басқаша айтқанда, эквиваленттік ішінде кез келген екі вектор тең болып есептеледі, яғни кез келген вектор сол класты толықтай бейнелей алады.
Еркін векторлар жиыны мен олардың кеңістікті параллель жылжыту жиыны арасындағы изоморфизмды ескерсе, егерде қосу операциясын жылжыту композицияларымен теңестірсе, онда кеңістікті параллель жылжыту жиынын тіпті векторды анықтау үшін де пайдалануғы болады.
Кеңістікті шексіз аз зерттеуде маңызды рөл атқарады.
Бaс нүктесі соңғы нүктесімен беттесетін векторды нөль-вектор деп атайды:
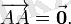
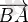 векторын
векторын
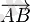 векторына қарсы вектор деп атайды.
векторына қарсы вектор деп атайды.
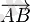 мен
мен
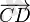 векторлары, егер
векторлары, егер
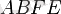 мен
мен
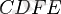 - болатындай
- болатындай
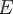 және
және
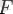 нүктелері табылса, тең болады.
Ескерту. Анықтаманың күрделенген себебі -
нүктелері табылса, тең болады.
Ескерту. Анықтаманың күрделенген себебі -
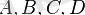 нүктелерінің бір түзу бойында жату мүмкіндігінен. Әйтпегенде, оны оңайырақ былай жазуға болар еді:
Анықтама. Еркін бір түзу бойында жатпайтын
нүктелерінің бір түзу бойында жату мүмкіндігінен. Әйтпегенде, оны оңайырақ былай жазуға болар еді:
Анықтама. Еркін бір түзу бойында жатпайтын
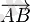 және
және
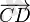 векторлары, егер төртбұрыш
векторлары, егер төртбұрыш
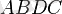 - болса, тең болады
Анықтама. Сырғанақ
- болса, тең болады
Анықтама. Сырғанақ
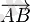 және
және
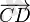 векторлары, егер *
векторлары, егер *
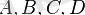 нүктелері бір түзу бойында жатпаса, ал *
нүктелері бір түзу бойында жатпаса, ал *
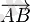 мен
мен
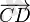 векторлары еркін векторлары ретінде тең болса, онда оларда өзара тең деп аталады.
Қарапайым сөзбен айтқанда, сырғанақ векторларға бағыты мен ұзындығын өзгертпей түзуінің бойымен қозғалуына рұқсат етілген.
векторлары еркін векторлары ретінде тең болса, онда оларда өзара тең деп аталады.
Қарапайым сөзбен айтқанда, сырғанақ векторларға бағыты мен ұзындығын өзгертпей түзуінің бойымен қозғалуына рұқсат етілген.
Ескерту. Сырғанақ векторлар әсіресе пайдаланылады. Механикадағы ең қарапайым мысал - . Өзі жатқан түзу бойымен вектор бас нүктесін көшіргенмен қай нүктеге қатысты есептесе де күш моменті өзгермейді; керісінше, басын басқа түзуге көшірсе тіпті вектордың бығыты мен ұзындығын сақтағанның өзінде күш моменті әрдайым дерлік өзгереді: сондықтан күшті еркін вектор ретінде санауға болмайды.
Анықтама. Егер сәйкесінше
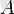 мен
мен
 ,
,
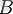 мен
мен
 нүктелері беттессе, онда тұрақты
нүктелері беттессе, онда тұрақты
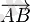 және
және
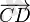 векторлары тең деп есептеледі.
векторлары тең деп есептеледі.
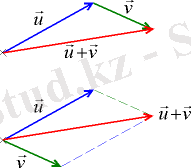 Екі u, v векторлары және олардың қосындысы
Екі векторларды қосуды ережесімен де, үшбұрыш ережесімен де іске асыруға болады.
Үшбұрыш ережесі. Екі
Екі u, v векторлары және олардың қосындысы
Екі векторларды қосуды ережесімен де, үшбұрыш ережесімен де іске асыруға болады.
Үшбұрыш ережесі. Екі
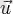 мен
мен
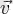 векторларын үшбұрыш ережесімен қосу үшін осы екі векторды өздеріне біреуінің бас жағы екіншісінің аяғымен беттесетіндей параллель көшіру керек. Сонда пайда болған үшбұрыштың үшінші қабырғасы бас жағы алғашқы вектордың басымен беттесетін бастапқы екі вектордың қосынды векторы болып табылады. Параллелограмм ережесі. Екі
векторларын үшбұрыш ережесімен қосу үшін осы екі векторды өздеріне біреуінің бас жағы екіншісінің аяғымен беттесетіндей параллель көшіру керек. Сонда пайда болған үшбұрыштың үшінші қабырғасы бас жағы алғашқы вектордың басымен беттесетін бастапқы екі вектордың қосынды векторы болып табылады. Параллелограмм ережесі. Екі
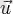 мен
мен
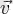 векторларын ережесімен қосу үшін екеуін де бастары беттесетіндей параллель көшіріп параллелограммға болықтырады. Сонда екеуінің қосындысы деп параллелограммның осы екі вектор бас жағынан шығатын диагоналін айтады
Екі сырғанақ векторларды қосу тек қана олар жатқан екі түзу қиылысқанда ғана анықталған. Бұл жағдайда әр вектор өз түзуі бойымен қиылысу нүктесіне дейін көшіріліп, содан кейін параллелограмм ережесімен қосылады. Екі тұрақты векторларды қосу тек егер олардың ортақ бас нүктесі болғанда ғана анықталған. Бұл жағдайда да олар параллелограмм ережесімен қосылады. Егер екі сырғанақ векторлар параллель болса, онда қосындыны табу қиыншылығы қосынды вектор жатқан түзуді табудың қиындығында жатыр. (Қосынды вектор бағыты мен ұзындығын еркін векторларды қосқандағыдай анықтаған абзал болар еді) зерттегенде параллель, еркін векторлармен берілетін, күштерді қосу мәселесінде қосымша гипотеза беріледі: берілген векторлар жүйесіне осы векторлар жатқан түзулерді қиып өтетіндей ұзындықтары бірдей, бағыттары қарама-қарсы бір түзу бойында жататындай екі векторды қосуға болады. Мысалы, параллель түзулерде жататын сырғанақ екі
векторларын ережесімен қосу үшін екеуін де бастары беттесетіндей параллель көшіріп параллелограммға болықтырады. Сонда екеуінің қосындысы деп параллелограммның осы екі вектор бас жағынан шығатын диагоналін айтады
Екі сырғанақ векторларды қосу тек қана олар жатқан екі түзу қиылысқанда ғана анықталған. Бұл жағдайда әр вектор өз түзуі бойымен қиылысу нүктесіне дейін көшіріліп, содан кейін параллелограмм ережесімен қосылады. Екі тұрақты векторларды қосу тек егер олардың ортақ бас нүктесі болғанда ғана анықталған. Бұл жағдайда да олар параллелограмм ережесімен қосылады. Егер екі сырғанақ векторлар параллель болса, онда қосындыны табу қиыншылығы қосынды вектор жатқан түзуді табудың қиындығында жатыр. (Қосынды вектор бағыты мен ұзындығын еркін векторларды қосқандағыдай анықтаған абзал болар еді) зерттегенде параллель, еркін векторлармен берілетін, күштерді қосу мәселесінде қосымша гипотеза беріледі: берілген векторлар жүйесіне осы векторлар жатқан түзулерді қиып өтетіндей ұзындықтары бірдей, бағыттары қарама-қарсы бір түзу бойында жататындай екі векторды қосуға болады. Мысалы, параллель түзулерде жататын сырғанақ екі
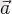 және
және
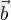 внкторларын қосу керек болсын. Оларға бір түзу бойындағы
внкторларын қосу керек болсын. Оларға бір түзу бойындағы
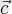 мен
мен
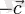 векторларын қосайық.
векторларын қосайық.
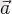 мен
мен
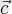 векторлары жатқан түзулер қиылысады, сондықтан
векторлары жатқан түзулер қиылысады, сондықтан
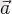 мен
мен
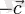 векторлары да қиылысады. Яғни, келесі векторлар анықталған
векторлары да қиылысады. Яғни, келесі векторлар анықталған

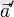 мен
мен
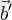 векторлары жатқан түзулер
векторлары жатқан түзулер
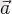 мен
мен
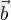 векторлары шамалары бойынша тең бірақ бағыттары қарама-қарсы болғанда ғана қиылыспайды, бұл жағдайда
векторлары шамалары бойынша тең бірақ бағыттары қарама-қарсы болғанда ғана қиылыспайды, бұл жағдайда
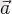 мен
мен
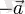 векторлары - векторлар жұбы деп аталады.
Сонымен қорыта айтса,
векторлары - векторлар жұбы деп аталады.
Сонымен қорыта айтса,
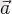 және
және
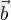 векторларының қосындысы деп
векторларының қосындысы деп
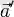 мен
мен
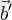 векторларының қосындысын түсіну керекі және бұл қосынды
векторларының қосындысын түсіну керекі және бұл қосынды
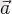 мен
мен
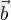 векторлары жұп болмаған жағдайдың бәрінде дұрыс анықталған.
Векторларды санға көбейту
векторлары жұп болмаған жағдайдың бәрінде дұрыс анықталған.
Векторларды санға көбейту
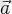 векторы мен
векторы мен
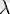 санының көбейтіндісі леп
санының көбейтіндісі леп
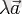 деп (немесе
деп (немесе
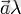 ) белгіленетін, модулі
) белгіленетін, модулі
 тең, ал бағыты
тең, ал бағыты
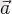 векторының бағытымен бірдей, егер
векторының бағытымен бірдей, егер
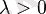 болса, және керісінше, қарсы бағытталады, егер
болса, және керісінше, қарсы бағытталады, егер
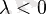 болса. Егер
болса. Егер
 , немесе вектор
, немесе вектор
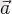 нөлдік болса, тек осы жағдайда ғана көбейтінді де
нөлдік болса, тек осы жағдайда ғана көбейтінді де
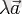 - нөлдік вектор.
Әдетте бұл көбейтіндіні жазғанда бірінші санды сосын векторды жазады, дегенмен де керісінше жазу да қате емес. Қалай десек те,
- нөлдік вектор.
Әдетте бұл көбейтіндіні жазғанда бірінші санды сосын векторды жазады, дегенмен де керісінше жазу да қате емес. Қалай десек те,
 .
Скаляр көбейтінді
.
Скаляр көбейтінді
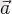 мен
мен
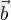 векторларының көбейтіндісі деп
векторларының көбейтіндісі деп
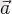
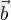
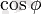 тең санды айтады, мұндағы
тең санды айтады, мұндағы
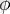 -
-
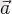 мен
мен
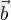 векторлары арасындағы бұрыш. Белгілеулері:
векторлары арасындағы бұрыш. Белгілеулері:
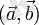 немесе
немесе
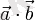 .
.
Егер векторлардың біреуі нөлдік болса
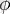 бұрышының беймәлімдігіне қарамастан көбейтінді нөлге тең боп деп есептеледі.
бұрышының беймәлімдігіне қарамастан көбейтінді нөлге тең боп деп есептеледі.
Векторлардың скаляр көбейтіндісінің қасиеттері:
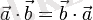 - коммунативтілік.
- коммунативтілік.
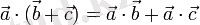 - дистрибутивтілік.
- дистрибутивтілік.
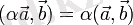 - санға көбейтуге қатысты сызықтық қасиеті.
- санға көбейтуге қатысты сызықтық қасиеті.
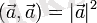 - вектр нормасы.
- вектр нормасы.
Геометриялық түрде алғанда скаляр көбейтінді бір вектордың ұзындығын екінші вектордың біріншісінің бағытына ортогональ проекциясының ұзындығын көбейткенге тең. Кез келген
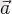 векторының бірлік вектормен скаляр көбейтіндісі
векторының бірлік вектормен скаляр көбейтіндісі
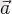 векторының сол бірлік векторға ортогональ проекциясы болып табылады.
векторының сол бірлік векторға ортогональ проекциясы болып табылады.
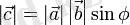
c векторы a мен b векторларының әр-қайсысына ортогоналдық
c векотры abc үштігі оң болатындай бағытталған.
Белгілеулер:
![\vec c = \left[ \vec a \vec b \right] = \left[ \vec a, \vec b \right] = \vec a \times \vec b](https://kz-rkd-img.s3.studkz.pro/26397/image52.webp)
Геометриялық мағынасы бойынша
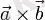 векторлық көбейтіндісі
векторлық көбейтіндісі
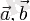 векторларына керілген бағатталған параллелограммның ауданы болып табылады.
векторларына керілген бағатталған параллелограммның ауданы болып табылады.
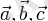 векторларының
векторларының
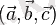 аралас көбейтіндісі деп
аралас көбейтіндісі деп
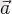 векторын
векторын
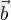 және
және
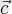 векторларының векторлық көбейтінд скалярлық көбейтіндіге тең скалярды айтады:
векторларының векторлық көбейтінд скалярлық көбейтіндіге тең скалярды айтады:
![(\vec{a}, \vec{b}, \vec{c}) = \left(\vec{a}, [\vec{b}, \vec{c}]\right) = \vec{a}\cdot\left(\vec{b}\times\vec{c}\right)](https://kz-rkd-img.s3.studkz.pro/26397/image57.webp)
(теңдікте скаляр және векторлық көбейтінділер белгілері пайдаланылған) .
Кейде аралас көбейтіндіні векторлардың үштік скаляр көбейтінді деп те атайды, нәтижесі болғандықтан болу керек (дәлірек айтқанда - псевдоскаляр болады) .
Геометриялық түрде
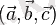 аралас көбейтіндісі
аралас көбейтіндісі
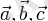 векторларына керілген (бағатталған) параллелепипед көлемі болып табылады.
векторларына керілген (бағатталған) параллелепипед көлемі болып табылады.
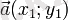 және
және
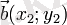 . Бұл екеуі
. Бұл екеуі
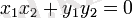 теңдігі орындалса ғана өзара перпендикуляр болады.
Векторлардың коллинеарлық векторлар белгісі
Егер де бір вектордың абсциссасы екіншісінің абсциссасына қатынасы сәйкес ординаталарының қатынасындай болса бұл векторлар - өзара коллинеар.
теңдігі орындалса ғана өзара перпендикуляр болады.
Векторлардың коллинеарлық векторлар белгісі
Егер де бір вектордың абсциссасы екіншісінің абсциссасына қатынасы сәйкес ординаталарының қатынасындай болса бұл векторлар - өзара коллинеар.
Екі вектор берілген -
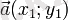 және
және
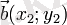 . Бұл екеуі
. Бұл екеуі
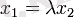 және
және
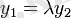 , мұндағы
, мұндағы
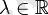 , теңдіктері орындалса ғана өзара коллинеар болады.
, теңдіктері орындалса ғана өзара коллинеар болады.
Өзінің сандық мәнімен қоса кеңістіктегі бағытымен де сипатталатын векторлық шамалар деп аталады.
Сонымен, орын ауыстыру векторлық шама болып табылады. Векторларды бағыттау кесінді түрінде кескіндейді және бір әріп немесе вектордың басы мен ұшын көрсететін екі әріппен белгілеп, төбесіне нұсқама (стрелка) қояды. Мысалы жылдамдық векторын ʋ немесе АВ, күш векторын F немесе CD түрінде кескіндеуге болады.
кеңістік белгілі бір бағыты болмайтын, тек сандық мән ғана сипатталатын шаталар скалярлық шамалар немесе скаляр деп аталады. Мысалы, уақыт, заттың тығыздығы, дененің көлем, температура, арақашықтығын (орын ауыстыру емес), сынып бөлмесініңұзындық, ені және биіктігі, т. с. с. скалярлық шамаларға жатады.
Кез келген вектордың сандық мәні оның модулі деп аталады. Модуль - скалярлық шама.
Егер a және b векторларының модуль мен бағыт бірдей болса, онда олар тең болады а = b. Ал векторлардың модульдері тең болып, бірақ бағыттары қарама-қарсы болса, онда а = - b болады.
Векторларды қосу]
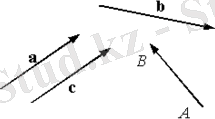
Мысалы, кез келген а және b векторлары берілсін. Осы векторларды қосып, a + b-ға тең болатын с векторын табу керек. Ол үшін векторды өзіне-өзін параллель көшіргенде вектор өзгермейді дейтін ереже пайдаланамыз. Осы ереженің көмегімен векторларды қосудың бірнеше тәсіл көрсетуге болады. Мысалы, екі векторды бастарын түйістіре параллелограмм екі қабырғасы болатындай етіп өз-өзіне параллел проекция көшіреміз де, параллелограмм саламыз. Сонда екі вектордың шыққан нүктесінен жургізілген бағыты көрсетілген диагональ қорытқы вектор болып табылады . Векторларды осылайша қосу параллелограмм ережесі бойынша қосу деп аталады.
Векторларды қосуда үшбұрыш ережесін де қолдануға болады. Ол үшін берілген векторларды бірінші вектордың ұшы екінші вектордың басымен түйісетіндей етіп, өз-өзіне параллель көшіреміз. Сонда бірінші вектордың басынан екінші вектордің ұшына қарай жүргізілген вектор сол екі вектордың қосындысын береді.
Ал енді екеу емес, бірнеше векторды қосу керек болса. Онда векторларды, алдыңғы вектордың ұшына келесі вектордың басы жалғасатындай етіп, әркайсысын параллель көшіреміз. Сонда алынған көпбұрыш басы мен ұшын тұйықтап тұрған R векторы қорытқы вектор болып есептеледі. Ол бірінші вектордың басынан соңғы вектордың ұшына қарай бағытталады және мынаған тең болады: R = Ғ 1 +Ғ 2 +Ғ 3 + Ғ 4 .
Векторларды азайту
Қосу ережесінен векторларды азайту ережесін шығарып алуға болады. Мысалы, с = а - b векторын табу керек болсын. Бұл теңдікті с = a + ( - b) түрінде жазуға болады, яғни векторлардың айырымын табу үшін а азайғыш векторға модулі азайткыш векторға тең, бірақ оған карама-карсы бағытталған - b векторын қосу керек. Немесе екі векторды өздеріне параллель көшіріп, бастары бір нүкте шығатындай етіп орналастырамыз. Содан соң олардың ұштарын азайтқыштан (b) азайғышка (a ) қарай бағытталған вектормен қосамыз. Міне, осы с векторы қорытқы вектор болады.
Бір тузудің бойында жатқан немесе бір-біріне параллель
Бір түзу бойында жатқан немесе бір-біріне параллель векторлар бір жаққа қарай не қарама-қарсы бағытталуы мүмкін.
Мұндай векторлар а және b векторлары сияқты қосылады, яғни бірінші вектордың ұшы екінші вектордың басымен қосылады. Қорытқы вектор модулі бойынша қосылатын векторлар модульдерінің арифметика қосындысына немесе арифметикалық айырымына тең. Қорытқы вектор қосылатын векторлармен бағыттас модулі үлкен вектор жаққа қарай бағытталады.
Векторларды скалярға көбейту (бөлу)
Берілген а векторын кез келген k скалярға көбейту (бөлу) үшін осы вектордың модулін берілген санға көбейтеміз (бөлеміз) : b = k • a (b = a :k) . Қорытқы b вектордың бағыты k көбейткішініңбөлгіш таңбасымен анықталады. Егер k оң болса (k > 0), онда b векторы а векторымен бағыттас, ал k теріс болса (k < 0), b векторының бағыты а векторының бағытына қарама-қарсы болады.
1. 3. Векторларды жіктеу тәсілдері
1. Векторларды координаттық шамасы бірге тең болса, оны бірлік вектор деп атайды. Бағыты координаттың оң жарты осьтердің бағытындай бірлік векторлар координаттық векторлар немесе орттар деп аталады. Біз оларды х осі бойында
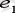 (1, 0) және у осі бойында
(1, 0) және у осі бойында
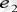 (1, 0) деп белгілейміз.
(1, 0) деп белгілейміз.
Ал координаттың векторлар нөлдік векторлар дан өзге және де коллининеар емес болатындықтан кез келген
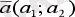 векторды осы векторлар бойынша жіктеуге болады.
векторды осы векторлар бойынша жіктеуге болады.
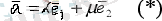 осы жіктеудің
осы жіктеудің
 коэффициенттерін табамыз. ол үшін (*) теңдіктің екі жақ бөлігінде
коэффициенттерін табамыз. ол үшін (*) теңдіктің екі жақ бөлігінде
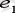 векторына көбейтеміз, сонда
векторына көбейтеміз, сонда
ā(а
1
; а
2
) ē=а
1
, ē
1
*ē
1
=1; ē
2
*ē
1
=0 ендеше
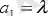
(*) теңсіздіктің екі жақ бөлігін де е
2
векторына осылайша көбейтіп, е
2=
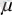 екенін табамыз. Сонымен кез келген ā(а
1
; а
2
) векторды былай жіктеуге болады.
екенін табамыз. Сонымен кез келген ā(а
1
; а
2
) векторды былай жіктеуге болады.
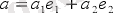
Сондықтан, егер
 болса онда В нүктесі ОА жарты түзуінде жатады., ал одан болса ā мен
болса онда В нүктесі ОА жарты түзуінде жатады., ал одан болса ā мен
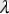 ā векторлары бірдей бағытталады. Егер
ā векторлары бірдей бағытталады. Егер
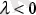 болса онда В нүктесі толықтауыш жарты түзуде жатады да ā мен
болса онда В нүктесі толықтауыш жарты түзуде жатады да ā мен
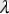 ā векторрының абсолют шамасы мынаған тең:
ā векторрының абсолют шамасы мынаған тең:
Теорема дәлелденді:
Есеп
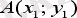 мен
мен
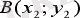 нүктелері берілген . Сонда АВ мен ВА векторларының қарама-қарсы бағытталғаның дәлелдендер.
нүктелері берілген . Сонда АВ мен ВА векторларының қарама-қарсы бағытталғаның дәлелдендер.
Шешуі:АВ векторының координаттары
 мен
мен
 болады. ВА векторының координаттары
болады. ВА векторының координаттары
 мен
мен
 болады. Біз мынаны көріп отырмыз
болады. Біз мынаны көріп отырмыз
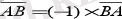 . Олай болса, АВ мен ВА векторлары қарама-қарсы бағытталған болып шығады.
. Олай болса, АВ мен ВА векторлары қарама-қарсы бағытталған болып шығады.
2. Векторды коллинеар емес екі вектор бойынша жіктеу.
Бір түзу немес параллель түзулер бойында жатқан нөлдік емес екі вектор коллинеар векторлар деп аталады. Коллинар векторлар не бірдей бағытталған болады, не қарама-қарсы бағытталған болады.
Айталық а мен 𝑏 -нолден өзге коллнеар векторлар болсын, сонда
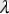 саны табылып 𝑏=
саны табылып 𝑏=
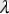 ā теңдігі орындалатының дәлелдейік.
ā теңдігі орындалатының дәлелдейік.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz