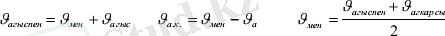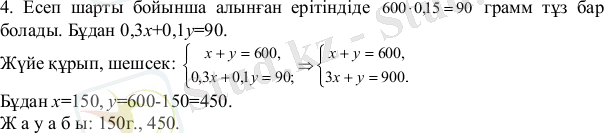Қоспаға (қорытпаларға) берілген есептер

Жоспар
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...2
І.Мәтінді есептер ұғымы ... ... ... ... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ...3
1.1.Мәтінді есептер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..3
1.2.Мәтіндік есептердің негізгі типтері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .6
ІІ.Қоспаға (қорытпаларға) берілген есептер ... ... ... ... ... ... ... ... ... ... ... ... 13
2.1. .Қоспаға берілген есептерге қойылатын талаптар ... ... ... ... ... ... ... ... ... ... ..14
2.2 Қоспаға берілген есептерді шешудің әдіс.тәсілдері ... ... ... ... ... ... ... ... ... ... 16
2.3. Қоспаға берілген есепті шешу процесі және оның негізгі кезеңдері ... ... ... 19
2.4. Қоспаға берілген есептердің шығарылу жолдары ... ... ... ... ... ... ... ... ... ... ...21
Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .25
Пайдаланылған әдебиеттер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...26

Кіріспе

Математика пәні мұғалімдерінің алдында тұрған сан алуан міндеттерінің бірі еліміздің халық шаруашылығын дамытудағы ғылыми – техникалық прогресті жетілдіруде, еліміздің материалдық техникалық базасын тереңдетуде, қоғамдық өндіріс дамуына оның тиімділігін арттыруда, математика ғылымының маңызы мен ролі жоғары екенін, математика ғылымы тіршіліктің тұтқасы, өмірдің негізі екенін көрсетіп, оқушы санасына сіңіру.
Осы міндетті шешудің бір жолы практикалық мазмұнды, мәселе есептерді шығарып үйрету.
«Қоспаға берілген есептер» тақырыбының өзектілігі–қоғамның қазіргі даму кезеңінен туындап отырған әлеуметтік сұранысқа орай оқушылардың жоғары логикалық ойлау қызметін жандандыру, зерттеушілік, ізденушілік қабілеттерін тәрбиелеу және қандай да болмасын бір мәселенің шешімін табудағы жаңашылдық пен шығармашылық дағдысын жетілдірудің қажеттілігімен айқындалады. Соңғы жылдары оқушылардың математика пәнін меңгеру деңгейі төмендеп кеткені байқалады. ҰБТ нәтижесі бойынша математика пәні оқушылардың ең төменгі деңгейде меңгерген сабақтарының қатарында тұр. Талдау нәтижелері мектеп бітірушілердің мәтінді есептерді шешу дағдыларының жеткіліксіздігін, есеп шартындағы әртүрлі элементтердің арасындағы байланыстарды өз беттерімен құра алу іскерліктерінің төмен екендіктерін көрсетті. Бұдан математиканы оқыту үрдісін жеке тұлғаға бағыттаудың, оқытудың практикалық тәсілдерінің түрлерін кеңейтудің, оқушылардың шығармашылық, зерттеушілік біліктіліктері мен дағдыларын, логикалық ойлау қабілеттерін дамытудың негізі ретінде оларды мәтінді есептермен жұмыс әдістеріне үйрету, есеп мазмұнын талдау және оны шығару кезеңдері мен тәсілдерін игертудің қажеттілігі туындайды.

Пайдаланылған әдебиеттер:

1. Т. А. Алдамұратова Математика 5- сынып
2. О.Р. Глейзер Математика тарихы 5-6- сынып
3. Т. А. Алдамұратова Математика (дидактикалық материалдар) 5- сынып
4. Т. А. Алдамұратова Математиканы оқыту әдістемесі 5- сынып
5. Математическая шкатулка
6. Баймолдаев Т.М., Ахметұлы.К. Жаңа буын оқулықтары арқылы жас ұрпаққа білім беру мен тәрбие беру жолдары. - Алматы. 2003.
7. Бағдарлама. Математика. Жалпы білім беретін мектептің 1-4 сыныптарына арналған. – Алматы, 2010.
8. Ведилина Е.А Обучение решению текстовых задач учащихся начальной школы. – Павлодар. 2006
9. Оспанов Т.Қ. және т.б. Математика. Жалпы білім беретін мектептің 3- сыныбына арналған оқулық – Алматы. 1998.
10. Өтепқалиев С. Оқушыларды мәтінді есептердің мағынасын талдауға үйрету. //Математика және физика. №4 - 2002.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 25 бет
Таңдаулыға:

Жоспар
Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .2
І.Мәтінді есептер ұғымы ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... 3
1.1.Мәтінді есептер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 3
1.2.Мәтіндік есептердің негізгі типтері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..6
ІІ.Қоспаға (қорытпаларға) берілген есептер ... ... ... ... ... ... ... ... ... ... ... ... .13
2.1. .Қоспаға берілген есептерге қойылатын талаптар ... ... ... ... ... ... ... ... ... ... ...14
2.2 Қоспаға берілген есептерді шешудің әдіс-тәсілдері ... ... ... ... ... . ... ... ... ... ...16
2.3. Қоспаға берілген есепті шешу процесі және оның негізгі кезеңдері ... ... ... 19
2.4. Қоспаға берілген есептердің шығарылу жолдары ... ... ... ... ... ... ... ... ... ... ...21
Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .25
Пайдаланылған әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...26

Кіріспе

Математика пәні мұғалімдерінің алдында тұрған сан алуан міндеттерінің бірі еліміздің халық шаруашылығын дамытудағы ғылыми - техникалық прогресті жетілдіруде, еліміздің материалдық техникалық базасын тереңдетуде, қоғамдық өндіріс дамуына оның тиімділігін арттыруда, математика ғылымының маңызы мен ролі жоғары екенін, математика ғылымы тіршіліктің тұтқасы, өмірдің негізі екенін көрсетіп, оқушы санасына сіңіру.
Осы міндетті шешудің бір жолы практикалық мазмұнды, мәселе есептерді шығарып үйрету.
Қоспаға берілген есептер тақырыбының өзектілігі - қоғамның қазіргі даму кезеңінен туындап отырған әлеуметтік сұранысқа орай оқушылардың жоғары логикалық ойлау қызметін жандандыру, зерттеушілік, ізденушілік қабілеттерін тәрбиелеу және қандай да болмасын бір мәселенің шешімін табудағы жаңашылдық пен шығармашылық дағдысын жетілдірудің қажеттілігімен айқындалады. Соңғы жылдары оқушылардың математика пәнін меңгеру деңгейі төмендеп кеткені байқалады. ҰБТ нәтижесі бойынша математика пәні оқушылардың ең төменгі деңгейде меңгерген сабақтарының қатарында тұр. Талдау нәтижелері мектеп бітірушілердің мәтінді есептерді шешу дағдыларының жеткіліксіздігін, есеп шартындағы әртүрлі элементтердің арасындағы байланыстарды өз беттерімен құра алу іскерліктерінің төмен екендіктерін көрсетті. Бұдан математиканы оқыту үрдісін жеке тұлғаға бағыттаудың, оқытудың практикалық тәсілдерінің түрлерін кеңейтудің, оқушылардың шығармашылық, зерттеушілік біліктіліктері мен дағдыларын, логикалық ойлау қабілеттерін дамытудың негізі ретінде оларды мәтінді есептермен жұмыс әдістеріне үйрету, есеп мазмұнын талдау және оны шығару кезеңдері мен тәсілдерін игертудің қажеттілігі туындайды.

І.Мәтінді есептер ұғымы
1.1.Мәтінді есептер

Мәтін есептерді тура талқылауды керек ететін арифметикалық тәсілдерді қолдана отырып шығарудың оқушылардың логикасын дамытуда берері зор және арифметикалық тәсілді жақсы меңгерген оқушы мәтін есептерге жылдам, әрі дұрыс теңдеу құра алатыны сөзсіз. Мектеп оқулықтарында бастауыш сыныптардан кейін арифметикалық тәсілге онша көп көңіл бөлінбейді, көбінесе алгебралық тәсілдермен, яғни теңдеулер немесе теңдеулер жүйесін құру арқылы мәтін есептер шығарылады. Осы мәліметтерді ескере отырып, мынадай мәліметтер ұсынғым келіп отыр:
1) мәтін есептерді шығаруға үйретуде көңіл бөлуге тиісті жайттар;
2) мәтін есептерді шығарудың бірнеше тәсілдері мен оларға әдістемелік нұсқаулар.
3) мәтін есептердің қазақша аудармасы. Мәтін есептерді шығартып үйрету барысында оқушылардың деңгейлері анықталуы тиіс және соның нәтижесін ескере отырып, мәтін есептерді шығаруда қиыншылыққа кездесетін оқушыларға қарапайым жеңіл есептерді шығартудан бастаған дұрыс. Есептің мағынасын, есепте берілген іс-әрекеттерді толығымен түсінуге, есептің шартын жазуға оқушыларды қалыптастыру керек. Содан кейін шығару тәсілдерін бекіткен дұрыс болады. Оқушылар қарапайым есептерді жақсы түсінгендіктен, олардың игерген білімдері білмейтін материалдарды игеруге жетектейді. Сонымен қатар математика пәнінен алынған білімді ӛмірде жиі қолдануға тура келетіндіктен, оқушыларға өмірмен байланысты есептерді шығаруға беруді ескерген жөн, бұл оқушылардың танымдылығы мен қызығушылығын арттыруға ықпал етеді. Есепті жеңу - ой жеңісі, жігерлік жеңісі болып табылады. Оқушыға нұсқау жасауда, мұғалім ең төменгі деңгейде нұсқау жасағаны дұрыс болар еді. Мұғалім мен оқушы арасындағы қарым-қатынас өзім жасауға көмектесіңіз түрінде болуы керек. Қиындатылған есептер шығарылмаса, онда сыныптың потенциалын жоғалтып алуымыз мүмкін. Мәтін есептерді шығару барысында есептер әр түрлі болып көрінгенімен көптеген есептерді бір жүйеге жатқызуға болады, яғни ол есептерді шығаруда ортақ тәсіл қолданылады. Негізінен мәтін есептерді үлкен екі топқа бөлуге болады:

1. Алгебралық моделі сызықтық теңдеулер жүйесі болып табылатын есептер.
Оның қарапайым түрлері:

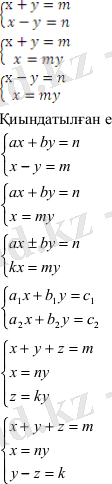
Мысалы:
Кептірілмеген саңырауқұлақтың құрамындағы су 99 %, ал кептірілген саңырауқұлақтың құрамындағы су 98%. Саңырауқұлақтың массасы
кептірілг еннен кейін қалай өзгереді?
Шешуі: Мысалы кептірілмеген саңырауқұлақтың массасы 100m кг болсын, онда оның құрамындағы сусыз бӛлік m болады. Кептіргеннен кейін құрамындағы құрғақ заттың массасы өзгерген жоқ, бірақ ол кептірілген саңырауқұлақтың 2%-ін құрады. Сондықтан кептірілген саңырауқұлақтың массасы 50m кг.
Мысал 2. Егер бір оң санды 1%-ға арттырып, ал екіншісін 4%-ға арттыра отырып қосындыны 3%-ға арттыруға бола ма?
Шешуі: Мысалы бірінші сан 100 болсын, ал екінші сан 200 болсын. Онда олардың қосындысы 300 болады. Сандарды арттырғаннан кейін бірінші сан 101, ал екінші сан 208 болады, онда екеуінің қосындысы 309 болады, яғни 3%-ға артады. Оқушыға бұл есепті түсіндіру үшін: егер бірінші санды 1%-ға емес, екінші сан сияқты оны да 4%-ға арттырсақ, онда қосынды 4%-ке артады. Яғни бірінші санды 3%-ға артық арттырғанымыз қосындыны 1%-ға артық арттырып тұр. Олай болса бірінші қосылғыштың пайызы қосындының пайызынан үш есе кіші. Егер бірінші қосылғыш қосындыдан үш есе кіші және екінші қосылғыштан екі есе кіші болуы тиіс.

1.2.Мәтіндік есептердің негізгі типтері

Жалпы орта білім беретін оқу бағдарламасында шешуі есеп шарты негізінде теңдеу (теңдеулер жүйесін) құруды талап ететін мәтінді есептердің әртүрі беріледі. Мұндай есептерді шеше білу көптеген факторларға байланысты. Дегенмен, ең алдымен есептердің негізгі типін ажырата білу және олардың қарапайым түрлерін шеше алу қажет. Соған байланысты типтік есептер мен олардың шешу әдістерін қарастыралық.Мәтінді есептерді негізінен төмендегідей типтерге бөлуге болады:қозғалысқа берілген есептер;
1) бірлескен жұмысқа берілген есептер;
2) жоспарлауға берілген есептер;
3) арифметикалық амалдардың компоненттері арасындағы
тәуелділікке берілген есептер;
4) процентке берілген есептер;
5) қоспаларға берілген есептер;
6) ерітіндіге берілген есептер;
7) әріпті коэффициенттері бар есептер;
8) тиімді шешімін табуға берілген есептер;
есептің басқа да түрлері. Қозғалысқа берілген есептерді шешкенде ескеретін жағдайлар:
1.Бұл типтегі есептердің негізгі компоненттері жүрілген жол (s),
жылдамдық , уақыт (t). Аталған шамалар арасындағы тәуелділік белгілі формулалармен өрнектеледі:

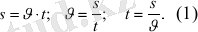
(көрсетілген шамалар өлшеу бірліктерінің бірыңғай жүйесінде: егер жол километрмен, ал уақыт сағатпен берілсе, онда жылдамдық кмсағ болуы
керек).
2. Есепті шығару жоспары мынандай:
а) Есеп шарты бойынша белгісіз шамалардың біреуін таңдаймыз және оны x, y, z т.с.с. белгілейміз.
б) Есеп шарты бойынша қай шама белгілі екендігін анықтаймыз.
в) (1) формулалардың көмегімен үшінші шаманы белгісіз х және белгілі
шама арқылы өрнектейміз.
г) Есеп шартының негізінде үшінші шаманың өзгерісі бойынша теңдеу
құрамыз.
3. Егер қандай да бір екі дене қозғалысын бірдей уақытта бастаса, олар кездескен жағдайда қозғалысты бастаған уақыттан кездескенге дейін бірдей уақыт жұмсайтынын байқаймыз. Егер бір дене екінші денені қуып жеткен жағдайда да осы жағдай орындалады.
4. Егер денелер қозғалысын әртүрлі уақытта бастаса, онда кездескенге дейін олардың қайсысы ерте шықса сонысы көп уақыт жұмсайды.
5. Өзендегі қозғалыста төмендегі формулаларды есте ұстау қажет:

Мысалы: Бір пункттен екінші пунктке қарай бір бағыттағы қозғалыс
Е с е п. Ара қашықтығы 18 км-ге тең А пунктінен В пунктіне қарай жаяу адам шықты. Оның артынан 2 сағаттан кейін, әр сағат сайын жаяу жолаушыға қарағанда 4,5 км-ге артық жол жүретін мотоциклші шықты.
Егер В пунктіне жаяу жолаушы мен мотоциклші бір уақытта жеткені белгілі болса, мотоциклшінің жылдамдығын табу керек.
Ш е ш у і.
Мотоциклшінің жылдамдығы: v1
Жаяу адамның жылдамдығы: v1- 4,5

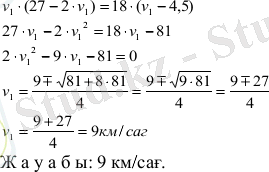
Бірлескен жұмысқа берілген есеп
1. Бұл типтегі есептердің негізгі компоненттері жұмыс, уақыт, еңбек өнімділігі (уақыт бірлігінде атқарылған жұмыс).
2. Есепті шешу жоспары төмендегідей болады:
а) Орындалуға тиісті барлық жұмысты 1 бірлік деп есептейміз.
б) Әр жұмысшының еңбек өнімділігін жеке-жеке табамыз, яғни 1tмұндағы t-аталған жұмысшы барлық жұмысты жеке өзі орындағанда жұмсалатын уақыт.
в) Әр жұмысшының өзі жеке жұмыс істеген уақытта барлық жұмыстың
қандай бөлігін орындағанын табамыз.
г) Барлық жұмыстың көлемін (1 бірлік) әр жұмысшының жеке жұмыс
істеген уақыттарында орындаған бөліктерінің қосындысына теңестіріп,
теңдеу құрамыз (егер есеп шартында барлық жұмысшы бірлесіп істегенде
жұмыс көлемінің толық орындалғаны көрсетілсе).

3. Мұндай есептерде әруақытта орындалған жұмыс салыстырылмайтынын
байқауға болады. Теңдеу құру үшін есеп шартында көрсетілген жұмсалған уақыт немесе еңбек өнімділігі қатынастары да негіз бола алады.
Жұмыс атқарылған белгісіз уақытты есептеу
Е с е п. Темір жолдың бөлігін екі бригада бірлесіп жұмыс істегенде 18
күнде жөндеуге тиіс еді. Нақтысында, алдымен тек бірінші бригада жұмысты жеке өзі бастап, екінші бригада жеке істеп аяқтады. Екінші бригаданың еңбек өнімділігі бірінші бригаданың еңбек өнімділігінен жоғары. Нәтижесінде жолдың бөлігін жөндеу жұмысы 40 күнге созылды. Сонда бірінші бригада өзі жұмыс істеген уақытта барлық жұмыстың 23 бөлігін орындады. Әр бригада жеке жұмыс істегенде аталған жұмысты неше күнде бітірер еді?
Ш е ш у і.
1. Барлық жұмысты бірінші бригада х күнде, ал екінші бригада у күнде
орындайды делік
делік.

Жоспарлауға берілген есеп
Бұл типтегі есептерге орындалатын жұмыс көлемі белгісіз немесе оны анықтау керек болатын есептер жатады (бірлескен жұмысқа берілген есептерден айырмашылығы). Мұнда жоспар бойынша орындалуға тиісті және нақты орындалған жұмыс салыстырылады. Бірлесіп істелген жұмыстағы сияқты жоспарлауға берілген есептердің де негізгі компоненттері:
а) жұмыс (нақты орындалған және жоспарланған);
б) жұмысты орындау уақыты (жоспарланған және нақты жұмсалған);
в) еңбек өнімділігі (нақты және жоспарланған).
Е с к е р т у. Кейбір есептерде жұмысты орындау уақытының орнына оны орындауға қатысатын жұмысшылар саны беріледі. Орындалатын жұмыстың көлемін анықтауға арналған есептер
Е с е п. Темір жонушының шәкірті шахмат комплектілерінің белгілі бір
саны үшін шахмат пешкілерін жонды. Оның күніне қазіргідегіден 2 пешкі артық жонуды үйренгісі келеді, сонда ол осындай тапсырманы 10 күнге тез бітірер еді. Егер ол күніне қазіргідегіден 4 пешкі артық жонуды үйренсе, онда осындай тапсырманы орындау мерзімі 16 күнге қысқарады. Егер әр комплектіге 16 пешкіден қажет болса, темір жонушы неше шахмат комплектісін пешкімен қамтамасыз ете алады?

Арифметикалық амалдардың компоненттері арасындағы тәуелділікке берілген есеп Әрқайсысы ізделінді қосындының берілген немесе басқа бөлігі болып табылатын қосылғыштардың қосындысын табу талап етілетін есеп

Проценттерге берілген есеп
Бұл типтегі есептер басқа типті есептерді шығарудың құрамдас бөлігі ретінде енгізіледі. Процентке берілген есептердің көбінесе мынадай үш типі кездеседі:
1) берілген санның процентін табу;
2) проценті бойынша санды табу;
3) екі санның проценттік қатынасын табу.
Проценттің анықтамасынан бірінші және екінші типтің есептері
(берілген санның процентін табу және проценті бойынша санды табу)
берілген санның бөлшегін табуға және берілген бөлшегі бойынша санды
табуға арналған есептерге сәйкес есептер ретінде оңай шығаралатындылығы

көрінеді.Процентті санның жүздік үлесінің сәйкес мөлшеріне ауыстыру арқылы
проценттерге берілген мұндай есептерді бөліктерге берілген есептерге
оңай келтіруге болады.Арифметикалық тәсілмен шығарылатын есеп

ІІ.Қоспаға (қорытпаларға) берілген есептер

Қоспаларға (қорытпаларға) берілген есеп Бұл типтегі есептер едәуір қиындық келтіреді. Есептің шартын түсініп, талдау ерекше маңызды. Мұндай есептерді бірнеше қарапайым есептерге жіктеу қажет. Қоспаның компоненттерінің қатынасы процентпен берілген есеп Е с е п. 30 %-тік және 10 %-тік тұз ерітінділерін араластығанда, 600 грамм 15 %-тік ерітінді алынды. Әр ерітіндіден қаншадан алынған? Ш е ш у і. 1. 30 %-тік ерітіндіден х грамм, 10 %-тік ерітіндіден у грамм алынды делік. 2. Есеп шартынан х+у=600 болатыны түсінікті. Бірінші ерітінді 30 %-тік болғандықтан оның құрамында 0,3х г. қышқыл бар. 3. Сол сияқты 10 %-тік у грамм ерітіндіде 0,1у г. қышқыл бар. 30.

2.1.Қоспаға берілген есептерге қойылатын талаптар

Қоспаға берілген есептерге қойылатын талаптарды айқындадық. Олар:
практикалық мазмұнды есептер және математикалық жаттығулар математика бағдарламасының талаптарына, оқушылардың білім, іскерлік, дағдыларына сай болуы тиіс;
олар оқушылардың танымдық қызығушылығын дамытуға бағытталған (қысқаша жазу, оған сызба сызу, кесте толтыру, сурет салу, қарапайым диаграммаларды, графиктерді оқу және сызу, практикалық жағдайларды модельдеу және т.б.) білім, іскерлік, дағдының қалыптасып, дамуына ықпал етуі қажет;
практикалық мазмұнды есептердің мазмұны оқушылар үшін таныс математикалық аппараттың практикада қолданылуын, сандық мәліметтерді пайдаланудың ерекшеліктерін (сандық мәліметтерінің шынайлығы, сұрақтардың қойылу дәрежесі, алынған жауаптың шындыққа сәйкес келуі) ашуы керек;
есептің мазмұнында оқушылар қабылдап, түсіне алатындай шынайы
мәліметтер болуы керек, оқушылардың өмірлік тәжірибелеріне, жас
ерекшелігіне, білім дәрежесіне және танымдық мүмкіндіктеріне сәйкес болуы қажет;
есептің сюжеті және сандық мәліметтері айналадағы шындықтың озық жақтарын, ғылым мен техниканың соңғы жетістіктеріндегі мәліметтерді бейнелеуі қажет; тәрбиелеушілік, танымдық сипатқа ие болып, математикаға қызығушылық тудыру керек;
сұрақтардың қойылу мәнері шынайы жағдайда туындауы мүмкін болатын сұраққа сай болуы керек (жете ме, жеткілікті ме, бола ма және т.б. );
практикалық мазмұнды есептер және оларға арналған тапсырмалар
оқушылардың танымдық іс-әрекеттерін (сезіну, зейін, қабылдау, еске сақтау,
қиял, ойлау, сөйлеу) дамыта алатындай болуы тиіс;
- есепті шығару әдістері оқушылардың өздері күнделікті тәжірибеде
пайдаланып жүрген әдістерге сәйкес немесе жақын болуы керек, оларды оқушыларға үйретуде көп уақытты алмауы қажет.
Осы талаптарды орындау бастауыш сынып оқушыларының танымдық қызығушылығының нәтижелі дамуына әсер етеді.
Қоспаға берілген есептерді қолданудың нақты әдістемелік ұсыныстары қарастырылды. Бұл кезеңде мынадай мәселелерге ерекше көңіл аударылды:
- есептің соңғы нәтижесін алуға ынталандыру арқылы практикалық мазмұнды есептерді шығаруға оқушылардың қызығушылығын оятып, математика пәніне сүйіспеншілігін тудыру;
- есептің мазмұнын, мағынасын түсіндіру, шартын талдау, белгілі және белгісіз компоненттерін бөлу, есепті шешуге ұсынылған тәсілдерді қарастыру;
- ұжыммен бірлесе отырып есепті шешу жоспарын құрастыру, есепті шешу және оны дәптер бетіне түсіру;
- есептің шешімін тексеру, алынған нәтиженің есеп шартымен үйлесуін анықтау, қажетті жағдайда есепті шығарудың қосымша тәсілдерін табу, оқушылар есепті шығару барысында өздеріне жаңа және практикалық маңызды қандай мәліметтерді пайдаланғандығын бөліп көрсету;
- практикалық мазмұнды есептерде қарастырылған мәселе бойынша келтірілетін түсіндірменің және соның барысында орындалатын ой жүйесінің үлгілерін жетекші сұрақтар арқылы бағыттау, сұрақ-жауаптар арқылы әңгімелесу;
- практикалық мазмұнды есептің мәтіні оқылысымен оқушылардың зейінін, ойын бір арнаға бағыттап, оны шешудің жоспарын кезінде талдау жасату;
- қоршаған ортадан алынған мағлұматтар бойынша есептер құрастыру және оны шығару, өмірмен байланыстырып талдау;
- есептің шартына байланысты оқушылардың шығармашылық іс-әрекетін ұйымдастыру (сурет салу, сызба сызу, кесте толтыру т.б.);
- берілген практикалық мазмұнды есептерді түрлендіре білу, жанама есептерді кері есепке айналдыру, салыстыру;
- Қоспаға берілген есептерді әр түрлі тәсілдермен шығару.

2.2.Қоспаға берілген есептерді шешудің әдіс-тәсілдері

Есепті шешу тәсілі негізінен, арифметикалық және алгебралық деп екіге бөлінеді. Арифметикалық әдісте есептің сұрағына жауапты берілген сандарға арифметикалық амалдар қолдану нәтижесінде табады. Есепті арифметикалық әдіспен шығару процесінде анализ - синтездік тәсіл кеңінен қолданылады. 9 Анализ - грек сөзі талдау, ажырату, ыдырату дегенді білдіреді. Анализ ғылыми танудың ақиқат нәрсені немесе логикалық объектіні құрамды бөліктерге ажырату арқылы зерттеп білетін әдіс. Синтез - грек сөзі біріктіру, байланыстыру, құрастыру дегенді білдіреді. Синтез нәрсені бүтін күйінде, оның бөліктерінің өзара байланысында, бірігуінде қарастырып зерттейтін әдіс. Есеп шығару процесінде анализ бен синтезді қатар қолданамыз. Сондықтан есеп шығарғанда таза анализ және таза синтез қолданылмайды. Олар көбінесе тығыз бірлікте не жалғасқан кезекте келіп отырады. Анализ әдісімен есептер шығарғанда, ең алдымен есептегі ізделіндіден, яғни есептің талабынан бастайды, содан кейін оны табу үшін нелерді білу керек (бұл анализ жолымен пайымдаудың негізгі сұрауы) деп іздеп, керекті шамаларды анықтайды. Егер бұл анықтайтындар есеп шартында берілген сандар болса, онда оларға қолданылатын амалдар орындалады да, есеп осы жолмен шығады. Егер ол анықталғандар тағы да белгісіз шамалар болып шықса, оны табу үшін әрі қарай нелерді білу керек деп іздеп, солар анықталады. Сөйтіп, есептегі берілгендерге келгенше осылайша пайымдау жолы жүргізіле береді. Синтез әдісімен есептер шығарғанда, әуелі есептегі берілгендерден бастайды. Берілгендер мен амалдарды орындап, аралық белгісіздер табылады. Содан кейін оларды білу нәтижесінде не білуге болады? деп іздей отырып, ақырында есептің сұрағына жауап беріледі.
Алгебралық талдау - есеп шығару процесін теңдеу тіліне көшіріп, "модельдеу" әдісі. Оның мәні сол, есеп шығарушы модельдер тізбегін құру арқылы нақты мазмұнды абстрактілі мазмұнға көшіреді. Мәселен, мәтінді есептердің мазмұны бойынша құрылған теңдеу оның аналитикалық моделі, ал сызба геометриялық моделі болып табылады. Есепті алгебралық әдіспен шешкенде есептің сұрағына жауапты теңдеу құру және оны шешу арқылы береді. Белгісізді әріппен белгілеп, түсінік беру барысына байланысты бір есепті шығарғанда әртүрлі теңдеу құруға және бұл жағдайда есептің әртүрлі алгебралық шешімі туралы айтуға болады. Қоспаға берілген есепті алгебралық тәсілмен шешу үшін оны математика ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.