Төртбұрыштар: анықтамалар, теоремалар, аудандары және элементтері бойынша салу


Жоспар
Кіріспе . . . 2
І. Төртбұрыштар.
1. 1. Төртбұрыштар туралы түсінік. Төртбұрыштардың ішкі бұрыштарының қосындысы . . . 3
1. 2. Параллелограмм және оның қасиеттері мен белгілері . . . 5
1. 3. Тіктөртбұрыш, ромб, квадрат және олардың қасиеттері . . . 7
1. 4. Трапеция және оның қасиеттері . . . 9
ІІ. Төртбұрыштардың аудандары.
2. 1. Тіктөртбұрыштардың аудандары . . . 10
2. 2. Параллелограммның ауданы . . . 13
2. 3. Трапецияның ауданы . . . 14
ІІІ. Төртбұрыштарды элементтері ойынша салу . . . 15
Қорытынды . . . 16
Пайдаланылған әдебиеттер . . . 18
Кіріспе
Қазіргі кезде бүкіл дүние жүзілік білім әлеміне кіру мақсатында Қазақcтанда білімнің жаңа жүйесі құрылуда . Бұл үрдіс педагогика теориясы мен оқу-тәрбие үрдісіне нақты өзгерістер енгізумен қатар жүргізіледі. Елімізде болып жатқан түрлі бағыттағы өзгерістер білім беру саласына жаңаша қарауда: мұғалімнің оқу -тәрбие үрдісін жаңаша тұрғыда ұйымдастыруды, оқушылардан танымдық, шығармашылық потенциялдық дамытуды талап етеді.
Қазақстан Республикасының «Білім туралы» заңында : «Білім беру жүйесінің басты міндеті ұлттық және жалпы адамзаттық құндылықтар, ғылым мен практика жетістіктері негізінде жеке адамды қалыптастыруға және кәсіби шыңдауға бағытталған білім алу үшін қажетті жағдайлар жасау, оқытудың жаңа технологияларын енгізу, білім беруді ақпараттандыру халықаралық ғаламдық коммуникациялық желілерге шығу» - деп білім беру жүйесін одан әрі дамыту міндеттерін көздейді. Бұл міндеттерді шешу үшін әр мұғалімде күнделікті ізденіс арқылы, барлық жаңалықтармен қатар тұру, өзгерістерге батыл жол ашарлық жаңа практикаға, жаңа қарым - қатынасқа өту қажеттілі туындайды
Міне, осындай маңызды мәселелерді шешуде жас ұрпақты сапалы да, саналы ой еңбегіне тәрбиелеуде математиканың алатын орны ерекше.
Бұл жұмыста төртбұрыштарлың түрлері мен қасиеттері ткралы айтылып, анықтамалар мен теоремалар дәлелденген. Геометриялық салулар мен төртбұрыштардың, рпараллелограм, ромб, квадрат және трапцияның аудандарын табу үшін дәлелденген теориялар мен анықтамалары берілген.
І. Төртбұрыштар.
1. 1. Төртбұрыштар туралы түсінік. Төртбұрыштардың ішкі бұрыштарының қосындысы.
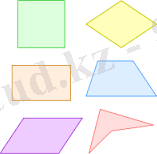 Анықтама. Әрбір үшеуі бір түзуде жатпайтын төрт нүктені тізбектей қосатын қиылыспайтын төрт кесіндіден және сол кесінділермен шектелген жазықтықтың бөлігінен тұратын фигураны төртбұрыш деп атайды.
Анықтама. Әрбір үшеуі бір түзуде жатпайтын төрт нүктені тізбектей қосатын қиылыспайтын төрт кесіндіден және сол кесінділермен шектелген жазықтықтың бөлігінен тұратын фигураны төртбұрыш деп атайды.
Басқаша айтқанда, әрбір үшеуі бір түзеуде жатпайтын А, В, С, D төрт нүкте берілсе, оларды тізбектей қосып, төртбұрыш аламыз. Оны АВСD деп белгілейміз. Жазықтықтың қарастырылып отырған бөлігі төртбұрыштың ішкі облысы деп аталады. А, В, С, D нүктелері оның төбелері, А В, СВ, СD, DА кесінділері қабырғалары. ∠АВС, ∠ВСD, ∠СDА∠ DАВ бұрыштары деп аталады. А мен С, В мен D-төртбұрыштың қарама қарсы төбелері. Қарама-қарсы төбелерді қосатын кесінділер(АС, ВD) диагональдар деп аталады. Ортақ қабырғалары жоқ бұрыштар төртбұрыштың ∠АВС мен ∠СDА, ∠ВСD мен
∠ DАВ қарама қарсы бұрыштары болып табылады. Сондай-ақ ортақ ұштары жоқ қабырғалар(АВ мен СD, ВС мен АD) қарама-қарсы қабырғалары деп аталады.
Сонымен төртбұрыштың төбесі, төрт қабырғасы және төрт бұрышы болады.
Төртбұрыштар дөңес және дөңес емес болып бөлінеді. Егер төртбұрыштың кез келген қабырғасы арқылы түзу сызық жүргізгенде, төртбұрыш сол түзумен шектелген жарты жазықтықтардың тек бірінде ғана жатса, онда ол дөңес деп, ал екі жарты жазықтықта жатса дөңес емес деп аталады. Төртбұрыштың қабырғаларының ұзындықтарының қосындысын оның периметрі деп атаймыз.
Теорема. Төртбұрыштың ішкі бұрыштарының қосындысы 360 0 -қа тең.
Дәлелдеу. АВСD төртбұрышы берілсін. АС диагоналі оны екі үшбұрышқа бөледі. АВС және АСD. Бұл үшбұрыштардың ішкі бұрыштарының қосындысы берілген төртбұрыштың ішкі бұрыштарының қосындысына тең. Әрбір үшбұрыштың ішкі бұрышының қосындысы 180 0 -тан екені белгілі. Сондықтан төртбұрыштың ішкі бұрыштарының қосындысы 360 0 -қа тең. Теорема дәлелденді.
1. 2. Параллелограмм және оның қасиеттері.
Қарама -қарсы қабырғалары қос-қотан параллель болатын төртбұрыш параллелограмм деп аталады. Параллелограмм-дөңес төртбұрыш. Шынында да, параллелограмм оның әрбір қабырғасы арқылы өтетін түзумен шектелген жарты жазықтықтардың тек бірінде ғана жатады.
Параллелограмның бір төбесінен қарсы жатқан қабырғасына түсірілген перпендекуляр оның биіктігі деп, ал биіктік түсірілген қабырға табаны деп аталады. DE AB, DK BC, демек, DE кесіндісі параллелограмның D төбесінен АВ қабырғасына түсірілген биіктігі болады.
Теорема. Параллелограмның қарама-қарсы қабырғалары тең.
Дәлелдеу. Теореманың ақиқаттығы АВС және АСD ұшбұрыштарының теңдігінен шығады. . Мұнда АС -ортақ қабырға, ∠1=∠2, ∠3=∠4 ішкі бұрыштар. Демек, АВ=DС, ВС=АD болады. Теорема дәлелденді.
Бұл теоремадан параллелограмның мынадай үш қасиеті шығады:
- Параллелограмның қарсы жатқан бұрыштары тең.
- Параллелограмның диагоналдары қиылысу нүктесінде тең екі бөлікке бөлінеді. СебебіΔ\mathrm{\Delta}АВО=Δ\mathrm{\Delta}СDО(АВ=DС), ∠1=∠2, ∠6=∠5, АО=ОС, ВО=ОD болады.
- Параллелогамның бір қабырғасына іргелес бұрыштарының қосындысы 1800-қа тең Бұл екі түзудің параллелдің елгісінен шығады.

Теорема
Егер дөңес төртұрыштың;
- қарама-қарсы қаырғалары тең болс, онда ол параллелограмм болады.
- қарама-қарсы бұрыштары тең болса, онда ол параллелограмм болады.
- диагоналдары қиылысу нүктесінде тең екіге бөлінсе, онда ол параллелограмм болады.
- бір қабырғасына іргелес бұрыштарының қосындысы 1800 -қа тең болса, онда ол параллелограмм болады.
Параллелограмның тағы бір белгісін келтірейік.
Теорема. Егер дөңес төртбұрыштардың қарама-қарсы екі қабырғасы тең және параллель болса, онда ол параллелограмм болады.
Дәлелдеу. АВСD дөңес төртбұрышты беріліп, АВ=DС, АВDС болатын. АD‖ВС болатының дәлелдейік. ∠1=∠2(АВ‖DС), АВ=DС, АС ортақ қабырға болатындықтан, үшбұрыштар теңдігінің 1-белсі бойынша АВС= Бұдан АD=ВС және айқыш бұрыштар ∠3=∠4 екені шығадыДемек АD‖ВС. Теорема длелденді.
1-мысал. Периметрі 144 лм, ал бір қабырғасы екіншісінен 30 дм үлкен болатын параллелограмның қабырғаларын табайық.
Шешуі:Параллелограмның қасиеті бойынша оның қарама-қарсы қабырғалары тең. Параллелограмның бір қабырғасын х-деп, ал екінші қабырғаын у деп белгілейік. Сонда есептің шартынан
Теңдеулер жүйесі шығады. Бұл жүйені шешіп, х=51, у=21 дм, 51 дм, 21 дм-ге тең
2-мысал. Берілген периметрі, диагоналі және оған қарсы жатқан бұрышы бойынша параллелограмм салайық.
Шешуі:Есеп шешілген және АВСD параллелограмы салынған делік. АВ қабырғасын соқып оның жалғасына ВС-ға тең ВЕ кесіндісін салайық Е нүктесін С төбесімен қосып ∠Е= ∠АВС болатындай АСЕ аламыз, себебі теңбүйірлі (ВЕ=ВС) үшбұрыш, ал АВС-сыртқы бұрыш(∠АВС=∠Е+∠С және ∠Е=∠С)
Сонымен есептің шешімі АС қабырғасы (параллелограмның диагоналі болатын) Е бұрышы және жарты периметрге тең. АЕ қабырғасы бойынша АСЕ үшбұрышын салуға келтіреді. Сондықтан біз екі қабырғасы (АЕ және АС) олардың біріне қарсы жатқан Е бұрышы бойынша үшбұрыш саламыз. Ол үшін, алдымен АВС бұрышының жартысына тең Е бұрышын салып, оның бір қабырғасына төбесінен бастап үлкен қабырға ЕА-ны өлшеп саламыз. Сонда үшбұрыштың 2 төбесін(Е және А) аламыз. Үшінші С төбесін табу үшін А нүктесін центр етіп, радиосы диагональге тең доға жүргіземіз. Осы доға мен бұрыштың екінші қабырғасының қиылысуында С нүктесін аламыз, ол үшбұрыштың үшінші төбесі.
∠ЕСВ =∠Е болатындай СВ сәулесін жүргізіп, В нүктесін табамыз. Шыққан АВС-ізделінді параллелограмның жартысы. Бұл ұшбұрышты параллелограмға толтырып, ізделінді параллелограмды аламыз.
1. 3. Тіктөртбұрыш, ромб, квадрат және оладың қасиеттері
Тіктөртбұрыш.
Барлық бұрыштары тік болатын параллелограмды тіктөртбұрыш деп атайды.
Тіктөртбұрыш параллелограмның дербес жағдайы болғандықтан,
параллелограмның барлық қасиеттер және ол туралы теоремалар тіктөртбұрыш үшін де орындалады. АВСD тіктөртбұрышының іргелес қабырғасы өзара перпендикуляр.
Теорема. Тіктөртбұрыштың диагоналдары тең болады.
Теорема. Егер параллелограмның диагоналдары тең болса, онда ол тіктөртбұрыш болады
Дәлелдеу . теореманы дәлелдеу үшін теңбүйірлі үшбұрыштың қасиетін и және үшбұрыштардың ішкі бұрыштарының қосындысы180 0 -қа тең болатынын пайдаланамыз. Мысалы:АВСD параллелограмында АС=ВD болса, онда АО=ОС=ОD. Бұдан АОD үшбұрышында ∠3=∠1, ОDС үшбұрышыныды ∠2=∠4 болады. Бірақ -да∠3+∠4+∠2+∠1=180 0- қа тең, яғни2(∠1+∠2) = 180 0 сонда ∠1+∠2=90 0
 Параллелограмның қасиеті бойынша оның қалған бұрыштары тік болады. . Осылайша АВСD-ның тіктөртбұрыш екені шығады. теорема дәлелденді.
Параллелограмның қасиеті бойынша оның қалған бұрыштары тік болады. . Осылайша АВСD-ның тіктөртбұрыш екені шығады. теорема дәлелденді.
Ромб.
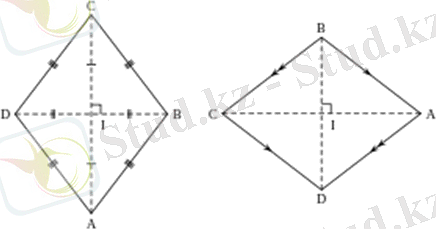
Барлық қабырғалары тең параллелограмм ромб деп аталады. Бұл суретте АВСD ромб бейнеленген. Ол параллелограмның дербес түрі болғандықтан, параллелограмның барлық қасиеттер және ол туралы теоремалар ромб үшін де орындалады. Мұндағы АВ =ВС=СD =DА.
Теорема. Ромбының диагональдары өзара перпендекулыр және олар бұрыштардың биссектрисалары болып табылады.
Дәлелдеу. АВСD ромб; АС, ВD оның диагональдары болсын. АС⊥ ВD. Бұдан ∠1=∠2. Осы сияқты ∠3=∠4 болатыны дәлелденеді. теорема дәлелденді.
Квадрат

. Барлық қабырғалары тең төртбұрыш. Квадрат тіктөртбұрыштың дербес түрі болғандықтан, төртбұрыштың барлық қасиеттері квадрат үшін орындалады. Квадратты барлық бұрыштары тік ромб деп те қарастыруға болады. Сондықтан квадраттың диагональдары перпендекуляр.
1. 4. Трапеция және оның қасиеттері.
Екі қабырғасы ғана параллель болатың дөңес төртбұрыш трапеция деп аталады.
Трапецияның параллель қабырғалары табандары, ал параллель емес қабырғалары бүйір қабырғалары деп аталады.
Бүйір қабырғалары тең трапеция тең бүйірлі трапеция деп аталады. Егер трапецияның бір бұрышы 900-қа тең болса, онда ол тікбұрышты трапеция болады. Трапецияның төбесінен түсірілген перпендикуляр оның биіктігі деп аталады.
Қарсы жатқан төбелерін қосатын кесінді трапецияның диагоналі деп аталады.
Трапецияның бүйір қабырғаларының ортасын қосатын кесіндіні трапецияның орта сызығы деп атайды.
Теорема. Трапецияның орта сызығы табандарына параллель және табандырының қосындысының жартысына тең.
Дәлелдеу. АВСD трапециясының ЕҒ орта сызығы болсын. ЕҒ‖АВ, ЕҒ‖DС және ЕҒ= (АВ+СD) болатының дәлелдейік.
АD бүйір қабырғасының ортасы Е нүктесі арқылы АВ және DС табандарына параллель түзу жүргізсек, ол ВС бүйірін Ғ нүктесінде қиып өтеді. АЕ=ЕD болғандықтан. Фалес теоремасы бойынша ВҒ=ҒС. Олай болса ЕҒ-трапецияның орта сызығы. Өзіміздің салуымыз бойынша ЕҒ‖АВ, ЕҒ‖DС. Демек, теореманың бірінші бөлігі дәлелденді.
Трапецияның ВD диагоналін жүргізсек Фалес теоремасы бойынша О нүктесі де ВD кесіндісінің ортасы болады. Ендеше ЕО және ОҒ кесінділері сәйкесінше АВD, ВСD үшбұрыштарының орта сызықтары:ЕО= АВ, ОҒ= DС оларды қоссақ, ЕҒ=ЕО+ОҒ= (АВ+СD) аламыз. Теорема дәлелденді.
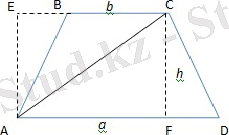
1-мысал. Диагоналі бүйір қабырғасына перпендикуляр және табанымен 200 бұрыш жасайтын теңбүйірлі трапецияның табанындағы бұрыштарын табайық.
Шешуі:АВСD трапеция. Теңбүйірлі трапецияның табандарындағы бұрыштары тең екені белгілі. ∠ВАD=∠СDА, ∠АВС=∠DСВ. Шарт бойынша,
АС⊥СD, ∠АСВ=20 0 демек, параллель түзулер мен қиюшының қасиеті бойынша ∠СDА=20 0 . ∠ВСD=∠ВСА+∠АСD=20 0 +90 0 =110 0 ал АD табанындағы бұрышы 70 0 болатынын таптық.
2-мысал. Теңбүйірлі трпапецияның қабырғаларының орталары ромбының төбелері болатының дәлелдейік.
Шешуі:Теңбүйірлі АВСD трапециясында АВ, ВС, СD, АD қабырғаларының орталары M, N, P, K нүктелері болсын. M мен N, P мен K нүктелерін кесінділермен қосайық және АС мен ВD диагональдарын жүргізейік. Сонда
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz