Санның модулі мен модуль таңбасы бар теңдеулер, теңсіздіктер және олардың графиктері


Жоспар
Кіріспе . . . 2
І. Модуль. Модуль анықтамасы
1. 1. Модуль. Модуль анықтамасы . . . 3
1. 2. Санның модулі . . . 4
ІІ. Модуль таңбасымен берілген теңдеулер мен теңсіздіктер.
2. 1. Модуль таңбасымен берілген теңдеулер мен теңсіздіктер . . . 5
2. 2. Модуль таңбасы бар теңдеулерді шешу . . . 9
2. 3. Модуль таңбасы бар теңсіздіктерді шешу . . . 11
2. 4. Модуль ішіндегі айнымалысы бар теңсіздіктерді шешу . . . 16
ІІІ. Модульге байланысты функция графигін тұрғызу . . . 20
Қорытынды . . . 23
Пайдаланылған әдебиеттер . . . 24
Кіріспе
Қазіргі заман математика ғылымының өте кең тараған кезеңі . Ал талапқа сай математикалық білім берудің басты шарты математикалық мәдениеттің деңгейін көтеру болып табылады.
Математикалық есептерді шешу, теоремаларды дәлелдеу оқушылардың ойын оятып, ойлау, есте сақтау қабілеттерін дамытуда, батыл қимылдар жасауға, шығармашылық ізденіске тәрбиелейді.
Ендеше оқушылардың математикаға дайындығын жан-жақты жетілдіру қазіргі аса маңызды міндеттердің бірі.
Бұл курстық жұмыста санның модулі туралы ұғым және оның қасиеттерін пайдаланып, модуль таңбасы бар теңдеулер мен теңсіздіктерді шешуді таңдап алдым. Себебі математикадан берілетін есептер ішінде модуль таңбасы бар теңдеулер мен теңсіздіктерді шешуге көптеп кездеседі. Бірақ бұл тақырыптың есептерін шешуге мектеп бағдарламасында сағат бөлінбеген . Сондықтан модуль таңбасы бар теңдеулер мен теңсіздіктерді шешудегі оқушылардың білімдері саяз болғандықтан ондай есептерді шешуде қиындыққа кездеседі. курстық жұмыста есептердің мазмұны, оқулықтағы және ҰБТ -дағы есептер. Есептердің шығарылу жолдары алдымен әртүрлі тәсілдермен көрсетіліп, ал қалған есептерді оқушылардың өздерінің тиімді тәсілді таңдап алуына баса назар аударылады. Шешімдерді іздеудің математикалық методтарын, логикалық пайымдаулардың, математикалық модельдердің, адекваттылық мәселелерін оқушылар меңгеріп алуларына зор көңіл бөлінеді.
І. Модуль. Модуль анықтамасы
1. 1. Модуль. Модуль анықтамасы
Модуль - (латынша - өлшем) - кез келген сан түріндегі сипаттамасы. Ауысу модулі - негізгі
 жүйесінен негізгі
жүйесінен негізгі
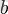 (көшу) кезінде логарифмдер көбейтілетін
(көшу) кезінде логарифмдер көбейтілетін
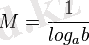 саны; натурал логарифмге ауысу (көшу) кезінде М =
саны; натурал логарифмге ауысу (көшу) кезінде М =
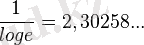 , ал ондық логарифмге ауысу кезінде
, ал ондық логарифмге ауысу кезінде
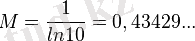 болады. модулі-
болады. модулі-
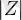 белгісімен өрнектелетін және
белгісімен өрнектелетін және
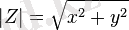 (мұндағы
(мұндағы
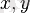 - нақты сандар және
- нақты сандар және
 -тің жорымал бөлігі, яғни
-тің жорымал бөлігі, яғни
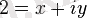 формуласымен анықталатын теріс емес сан (оң сан немесе нөл) . Нақты санның модулі -
формуласымен анықталатын теріс емес сан (оң сан немесе нөл) . Нақты санның модулі -
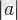 белгісімен өрнектелетін,
белгісімен өрнектелетін,
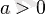 болған жағдайда
болған жағдайда
 -ға тең, ал
-ға тең, ал
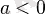 болса, -
болса, -
 -ға тең теріс емес сан. Салыстырылатын екі бүтін санның айырымы бөлінетін сан; "mod" болып белгіленеді; сонда
-ға тең теріс емес сан. Салыстырылатын екі бүтін санның айырымы бөлінетін сан; "mod" болып белгіленеді; сонда
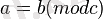 өрнегі
өрнегі
 айырымы
айырымы
 -ға бөлінеді дегенді
-ға бөлінеді дегенді
1. 1. Санның модулі
Нақты а санының модулі (абсолют шамасы) деп а О болғанда ол санның ѳзі, және а 0, болғанда қарама-қарсы а саны аталады. А санының модулі а болып белгіленеді. Сонымен
а=
Мысалы:-3=-(-3) =, өйткені -3 ; 3=3, өйткені 3
Геометриялық тұрғыдан а координаталық түзуде а нүктесінің 0 нүктесінен қашықтығын білдіреді.
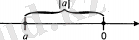
Сонымен санақ басынан сан тұрған нүктеге дейінгі ара қашықтық санның модулі деп аталады.
х=0, 5 теңдеуінің екі түбірі бар:
х=0, 5 және х=-0, 5, яғни -0, 5 және 0, 5 нүктелерінен 0-ге дейінгі арақашықтығы бірдей.
х=-0, 5 теңдеуініңи түбірі болмайды, себебі арақашықтық-теріс емес сан.
Егер:
1) Модульдері бірдей
2) таңбалары әртүрлі болса, онда екі сан қарама қарсы сандар деп аталады.
Мысалы, -5, 2 және 5 сандары-қарама қарсы сандар:олардың модульдері бірдей, таңбалары әртүрлі.
Сан алдында тұрған «-» таңбасы әрқашан берілген санға қарама қарсы санды білдіреді деп ұйғарамыз. Мысалы, -а жазуы а санына қарама қарсы сан дегенді білдіреді.
-а санының оң болуы да, теріс болуы да, нөл болы да мүмкін. Барлығы а санының бастапқыда неге тең болғанына байланысты. Егер а=3, 2 болса, онда оған қарама -қарсы -а саны теріс -3, 2 санына тең. Егер а=-8 болса, онда оған қарама-қарсы - саны оң -(-8) =8 санына тең.
Егер а=0 болса, онда оған қарама-қарсы -а саны 0-ге тең
Натурал сандар, нөл және натурал сандарға қарама-қарсы сандар бүтін сандар деп аталады. Мысалы:2-бүтін сан, өйткені натурал сан -8-бүтін сан, өйткені натурал санға қарама-қарсы; 0-анықтама бойынша бүтін сан; 5, 6 саны бүтін емес, себебі бұл сан натурал сан емес, натурал санға және 0 санына қарама-қарсы емес.
ІІ. Модуль таңбасымен берілген теңдеулер мен теңсіздіктер
1. 1. Модуль таңбасымен берілген теңдеулер мен теңсіздіктер
Нақты а санының модулі (абсолют шамасы) деп а О болғанда ол санның ѳзі, және а 0, болғанда қарама-қарсы а саны аталады. А санының модулі а болып белгіленеді. Сонымен
а=
Мысалы:π-3 =π-3, өйткені :π-3
-3, 7=-(-3, 7) =3, 7, өйткені -3, 7
Геометриялық тұрғыдан а координаталық түзуде а нүктесінің 0 нүктесінен қашықтығын білдіреді.
Мысалы:-3, 2 дегеніміз-0 нүктесінен сандар түзуін де белгіленген (-3, 2) нүктесіне дейінгі арақашықтық.
Модульдердің қасиеттері:
а ; а=-а; а𝑏=а*𝑏
а 2 = а2; а:𝑏=а:𝑏 0
х-а=𝑏 түріндегі теңдеуді геометриялық жолмен де шешуге болады.
1-мысал
х-5, 8=-3, 1 теңдеуін шешейік
х-5, 8=-3, 1 дегеніміз 0 нүктесінен 0, 2𝑧+2, 8 нүктесіне дейінгі арақашықтық 3, 1 -ге тең дегенді білдіреді. Ондай нүкте сандық осьте екеу:-3, 1 және 3, 1
Сондықтан келесі екі теңдеуді шешеміз:
0, 2𝑧+2, 8=3, 1
0, 2𝑧+2, 8=-3, 1
Егер 0, 2𝑧+2, 8=3, 1 болса, онда 0, 2𝑧=0, 3; 𝑧=1, 5
Егер 0, 2𝑧+2, 8=-3, 1 болса онда 0, 2𝑧=-5, 9; 𝑧=-29, 5
Жауабы: 𝑧 1 =1, 5, 𝑧 2 =-29, 5
k-3, 7 7, 2 теңсіздігін шешейік.
Бұл теңсіздікті -7, 2 екі еселі теңсіздігі түрінде жазуға болады.
Теңсіздіктердің негізгі қасиеттерін ескеріп, теңсіздік мүшелеріне 3, 7 санын қоссақ: -3, 5 екі еселі теңсіздігін аламыз
Жауабы:k=[-3, 5; 10, 9]
Бұл есепті графиктік тәсілмен шешейік.
Егер k-3, 7 онда k-3, 7 =k-3, 7 және k-3, 7 7, 2 теңсіздігін шешу керек:

Демек, (-3, 5) -тен10, 9 аралығында жатқан k-ның кез - келген мәні теңсіздікті қанағаттандырады.
Жауабы: -3, 5 k .
Сонымен қатар теңсіздіктің екі жағын да квадрат дәрежеге шығару әдісін пайдалануға болады, ол келесі тұжырымға негізделген.
Теорема. Егер (х) пен g (х) өрнектері кез келген х үшін тек теріс емес мәндерді ғана қабылдаса, онда (х) g (х) пен ( (х) ) 2 ( g (х) ) 2 теңсіздіктері пара пар. Бұл теорема модульдерді қамтитын теңсіздіктерді шешуде былай қолданылады.
(х) g (х) теңсіздігін шешу керек болсын.
(х) g (х) өрнектерінің анықталу облысындағы кез келген
х үшін (х) 0
g (х) 0, (х) 2 = (х) ) 2
Және g (х) 2 =( g (х) ) 2 қатыстары орынды болғандықтан, берілген теңсіздік
( (х) ) 2 ( g (х) ) 2
Теңсіздігіне парапар.
Х-1 теңсіздігін шешейік.
Берілген теңсіздікті екі жағынан да квадрат дәрежеге шығарып, оған парапар (х-1) 2 теңсіздігін аламыз. Соңғы теңсіздікті шеше отырып,
х 2 -2х-3 қатысын аламыз бұдан -1 екенін табамыз.
2Х-1 3х+1 теңсіздігін шешу керек.
Теңсіздіктің екі жағынан да квадрат дәрежеге шығара отырып, оған парапар
(2х-1) 2 (3х+1) теңсіздігін аламыз. Соңғы теңсіздікті түрлендіріп, 5х 2 +10х қатысын аламыз, бұдан х екенін табамыз.
Сонда берілген теңсіздіктің шешімі:
х
2. 2. Модуль таңбасы бар теңдеулерді шешу
Модуль таңбасы бар теңдеулерді шешудің бірнеше тәсілі бар. Оларды мысалдар арқылы қарастырайық.
1-мысал.
 =2 теңдеуінің түбірлерін табу керек.
=2 теңдеуінің түбірлерін табу керек.
Шешуі. 1-тәсіл. (Геометриялық тәсіл) .
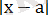 өрнегінің геометриялық мағынасы - ол сан осіндегі х нүктесінен а нүктесіне дейінгі қашықтықты білдіреді. Онда
өрнегінің геометриялық мағынасы - ол сан осіндегі х нүктесінен а нүктесіне дейінгі қашықтықты білдіреді. Онда
 =2 теңдеуінің геометриялық мағынасы х және 1 нүктелерінің ара қашықтығы 2-ге тең болатындығында. Олай болса, х=-1 немесе х=3 болуы керек.
=2 теңдеуінің геометриялық мағынасы х және 1 нүктелерінің ара қашықтығы 2-ге тең болатындығында. Олай болса, х=-1 немесе х=3 болуы керек.
Ж а у а б ы : х=-1; х=3.
2-тәсіл. ( Квадраттау тәсілі ) . Берілген теңдеудің екі жақ бөлігі де оң болғандықтан, оны квадраттап,
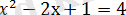 немесе
немесе
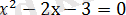 квадрат теңдеуін аламыз. Оның түбірлері:
квадрат теңдеуін аламыз. Оның түбірлері:
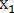 =-1 және
=-1 және
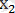 =3. Бұлар берілген есептің жауаптары.
=3. Бұлар берілген есептің жауаптары.
3-тәсіл. ( Анықтама тәсілі) . Анықтама бойынша
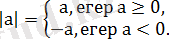
Осыдан, егер х-1 ≥ 0 болса, онда
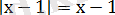 теңдігі және х-1<0 болса, онда
теңдігі және х-1<0 болса, онда
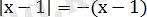 теңдігі орындалады. Сондықтан сан осін х=1 нүктесі арқылы екі бөлікке бөлеміз: (- ∞; +∞) =(- ∞; 1)
теңдігі орындалады. Сондықтан сан осін х=1 нүктесі арқылы екі бөлікке бөлеміз: (- ∞; +∞) =(- ∞; 1)
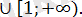 Осы бөліктің әрқайсысында берілген теңдеуді жеке шешу керек.
Осы бөліктің әрқайсысында берілген теңдеуді жеке шешу керек.
Егер х
 (-
(-
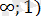 болса, онда берілген теңдеуді -х+2 түрінде жазамыз. Осыдан х =-1 болады.
болса, онда берілген теңдеуді -х+2 түрінде жазамыз. Осыдан х =-1 болады.
Егер х
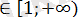 болса, онда берілген теңдеуді х-1=2 түрінде жазып, оның түбірін табамыз: х=3.
болса, онда берілген теңдеуді х-1=2 түрінде жазып, оның түбірін табамыз: х=3.
Ж а у а б ы : х=-1; х=3.
Шешуі. Мүнда
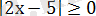 болғандықтан, х-1
болғандықтан, х-1
 болуы керек. Сондықтан бұл теңдеуді мынадай екі жүйеге бөлеміз:
болуы керек. Сондықтан бұл теңдеуді мынадай екі жүйеге бөлеміз:
- 2)
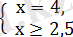
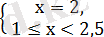
Ж а у а б ы :
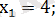
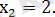
3-мысал.
 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі. Теңдеудің екі жақ бөлігі де оң болғандықтан, оны квадраттау тәсілімен шешкен тиімді.
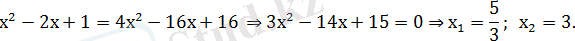
Ж а у а б ы :
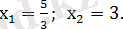
4-мысал.
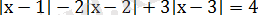 теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі. Мұндай теңдеулерді шешу үшін модуль таңбасы астындағы екімүшелерді нөлге теңестіріп, олардың түбірлерін анықтаймыз:
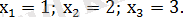 Онда бұл нүктелер сан осін 4 бөлікке бөледі:
Онда бұл нүктелер сан осін 4 бөлікке бөледі:
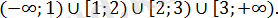
Егер
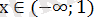 болса, онда
болса, онда
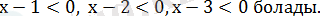 Сондықтан берілген теңдеуді
Сондықтан берілген теңдеуді
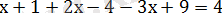 немесе
немесе
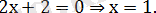 Ал х
Ал х
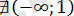 болғандықтан, бұл аралықта теңдеудің шешімі жоқ:
болғандықтан, бұл аралықта теңдеудің шешімі жоқ:

Егер
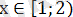 болса, онда
болса, онда
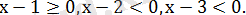 Олай болса, берілген теңдеуден мынаны аламыз:
Олай болса, берілген теңдеуден мынаны аламыз:
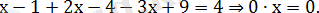 Бұл теңдік х-тің әрбір мәнінде орындалады. Онда бұл аралықта шешім
Бұл теңдік х-тің әрбір мәнінде орындалады. Онда бұл аралықта шешім
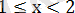 теңсіздігімен анықталады.
теңсіздігімен анықталады.
Егер
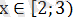 болса, онда
болса, онда
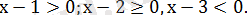 Сондықтан берілген теңдеуді
Сондықтан берілген теңдеуді
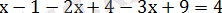 немесе
немесе
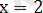 түрінде жазамыз. Онда есептің бұл аралықтағы шешімі
түрінде жазамыз. Онда есептің бұл аралықтағы шешімі
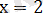 болады.
болады.
Егер
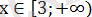 жағдайында
жағдайында
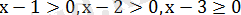 болады. Онда
болады. Онда
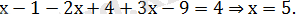
Мұнда
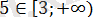 болғандықтан, шешімі
болғандықтан, шешімі
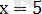 болады.
болады.
Ж а у а б ы:
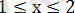 немесе
немесе
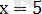 , яғни
, яғни
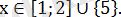
(
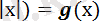 f түріндегі теңдеу
f түріндегі теңдеу
(мұндағы f
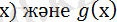 (қандай да бір рационал өрнектер)
(қандай да бір рационал өрнектер)
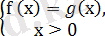 және
және
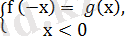 жүйесі түрінде жазуға болады.
жүйесі түрінде жазуға болады.
Мысалы:
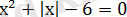
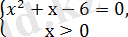 және
және
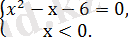
 теңдеуінің екі түбірі бар: -3 және 2.
теңдеуінің екі түбірі бар: -3 және 2.
 теңдеуінің екі түбірі бар: 3 және -2.
теңдеуінің екі түбірі бар: 3 және -2.
 Бірінші жүйенің шешімі:
Бірінші жүйенің шешімі:
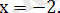 Екінші жүйенің шешімі:
Екінші жүйенің шешімі:
Теңдеудің шешімі: 2 және -2 болады.
Ескерту
: Берілген теңдеуді жаңа айнымалы еңгізу арқылы шешуге болады.
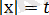 деп белгілесек, онда
деп белгілесек, онда
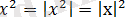 теңдеуді мына түрде жазуға болады:
теңдеуді мына түрде жазуға болады:
 Түбірлері: -3 және 2. Шешім ретінде 2 саны алынады:
Түбірлері: -3 және 2. Шешім ретінде 2 саны алынады:
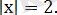 Олай болса
Олай болса
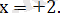
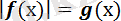 түріндегі теңдеуді шешу
түріндегі теңдеуді шешу
Теңдеуді мынадай жүйелер түрінде жазамыз:
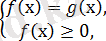 және
және
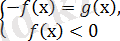
Мысалы:
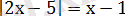 теңдеуін шеейек.
теңдеуін шеейек.
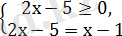 және
және
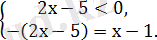
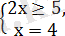 және
және
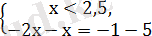
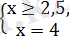 және
және
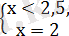
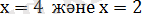 теңдеудің шешімі болады.
теңдеудің шешімі болады.
Екінші тәсіл:
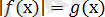 болса, онда
болса, онда
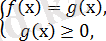 және
және
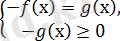 болады.
болады.
Ескерту:
Егер
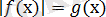 теңдеуінде f`(х) функциясы g(х) функциясына қарағанда қарапайым болса, онда теңдеуді екінші тәсілмен шығаруға ыңғайлы.
теңдеуінде f`(х) функциясы g(х) функциясына қарағанда қарапайым болса, онда теңдеуді екінші тәсілмен шығаруға ыңғайлы.
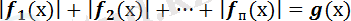 түріндегі теңдеуді шешу
түріндегі теңдеуді шешу
Мұндай теңдеулерді шешкенде үзіліссіз функцияның монотонды аралықтағы қасиетін пайдаланған қолайлы.
Мысалы:

Модуль таңбасының ішіндегі өрнектерді функция деп есептеп, нөлдерін табайық.
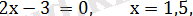


Сан осі төрт аралыққа бөлінеді.
0, 25 0, 5 3
1)
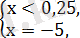 х
х
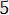
2)
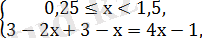
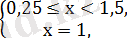 х
х
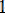
3)
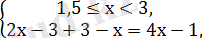
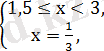 Шешімі жоқ
Шешімі жоқ
4)
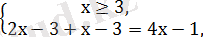
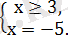 Шешімі жоқ Жауабы: -5 және 1.
Шешімі жоқ Жауабы: -5 және 1.
Мысалы: x-1+2=1
Теңдеуді шешу үшін жаңа айнымалы енгізуге болады. x-1=у.
Теңдеуді мына түрде жазылады:
y+2=1. Шешу жолы:
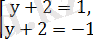
Сонда:
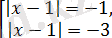
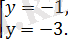
Теңдеудің шешім жоқ, себебі санның модулі теріс сан.
Жауабы: шешімі жоқ.
Мысалы: 2х+1

Теңдеуді екі жүйе құрып шешу керек. (1) формулаға қара.
Мысалы: Теңдеулер жүйесін шешіңдер
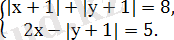
Екінші теңдеуден у+1-ді х арқылы өрнектеп, бірінші теңдеуге қоямыз.
Сонда:
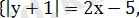
 болады.
болады.
х+1+2х-5
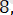 у+1
у+1

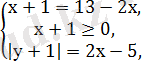
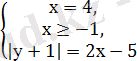
Жауабы: (4; 2), (4, -4)
2. 3. Модуль таңбасы бар теңсіздіктерді шешу
Модуль таңбасы бар теңсіздіктерді шешудің әртүрлі әдісі бар. Соның ішінде қолайлысы интервалдар әдісі.
1-мысал.
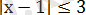 теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі.
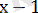 өрнегін нөлге айналдыратын х-тің мәнін табамыз, яғни
өрнегін нөлге айналдыратын х-тің мәнін табамыз, яғни
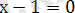 осыдан
осыдан
 Сан түзуінде
Сан түзуінде
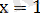 нүктесін белгілейміз.
нүктесін белгілейміз.
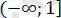 аралығын қарастырамыз. Бұл аралықта х-1 өрнегінің таңбасы теріс, яғни
аралығын қарастырамыз. Бұл аралықта х-1 өрнегінің таңбасы теріс, яғни
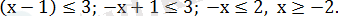
Бұл аралықтағы шешім:
 .
.
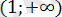 аралығын қарастырайық. Бұл аралықта х-1 өрнегінің таңбасы оң, яғни
аралығын қарастырайық. Бұл аралықта х-1 өрнегінің таңбасы оң, яғни
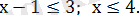 Бұл аралықтағы шешім
Бұл аралықтағы шешім
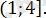
Ж а у а б ы :
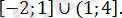
2-мысал.
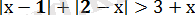
Шешуі. Мұнда
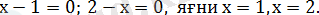
- аралығындаөрнегінің таңбасы теріс, алөрнегінің
таңбасы оң, яғни
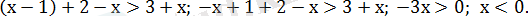
Бұл аралықтағы шешім
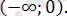
- аралығында; ұқсас мүшелерді біріктерсекяғни шешімі жоқ.
- аралығындаұқсас мүшелерді біріктерсек
- Ж а у а б ы :
f(x) <g(x), түріндегі теңсіздіктерді шешу, мұндағы f(x), g(x) - қандай да бір функция
Берілген теңсіздіктердің шешімі:
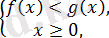 және
және
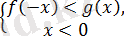 теңсіздіктер жүйелерін қанағаттандырады.
теңсіздіктер жүйелерін қанағаттандырады.
Теңсіздікті шешіңдер:
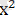 -5х+6<0
-5х+6<0
Берілген теңсіздіктің шешімі мына теңсіздіктер жүйелерін қанағаттандырады
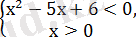 және
және
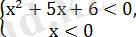
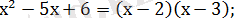 (х-2) (х-3)
(х-2) (х-3)
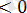
+ - +
х
2 3
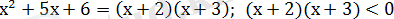
+ - +
х
-3 -2
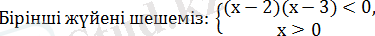
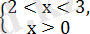
сонда
2
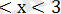
Екінші жүйені шешеміз:
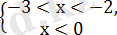 сонда
-3
сонда
-3
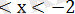
Жауабы: (-3; -2)
 (2; 3)
(2; 3)
Ескерту: Теңсіздікті жаңа айнымалы енгізу арқылы шешугі болады .
t=x,
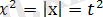 ,
,
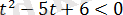
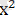 -5х+6<0
-5х+6<0
Берілген теңсіздіктің шешімі мына теңсіздіктер жүйелерін қанағаттандырады
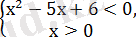 және
және
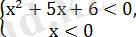
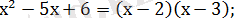 (х-2) (х-3)
(х-2) (х-3)
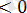
+ - +
х
2 3
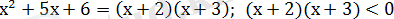
+ - +
х
-3 -2
сонда
2
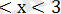
Екінші жүйені шешеміз:
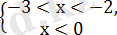 сонда
-3
сонда
-3
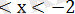
Жауабы: (-3; -2)
(2; 3)
Ескерту: Теңсіздікті жаңа айнымалы енгізу арқылы шешугі болады .
t=x,
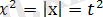 ,
,
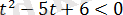 .
.
f(x
 )
)
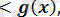 түріндегі теңсіздікті шешу, мұндағы f(x), g(x) - қандай да бір функциялар
түріндегі теңсіздікті шешу, мұндағы f(x), g(x) - қандай да бір функциялар
Берілген теңсіздіктің шешімі:
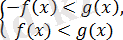 теңсіздіктер жүйелерін қанағаттандырады.
теңсіздіктер жүйелерін қанағаттандырады.
g(x)
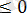 болса, берілген теңсіздіктің шешімі жоқ.
болса, берілген теңсіздіктің шешімі жоқ.
Теңсіздікті шешіңдер:
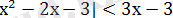
Мынадай теңсіздіктер жүйесін құрамыз:
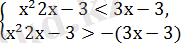
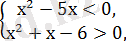
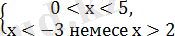
2
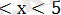
х(х-5)
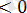

+ - +
(х-2) (х+3)
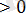
Жауабы: (2; 5)
Екінші тәсіл: Теңсіздіктің шешімі мына жүйелерді қанағаттандыру керек:
f(x)
түріндегі теңсздіктерді шешу
f(x)
мұндағы f(x),
- х айнымалысына тәуелді өрнектер, мына теңсіздіктерге байланысты шешіледі:
f(x)
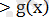 және f(x)
және f(x)
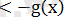 , яғни
, яғни
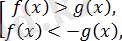
- Теңсіздікті шешіңдер:
х-1+х-5
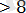
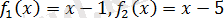
функцияларды нөлге теңестіріп шешеміз: x=1, x=5.
Осы нүктелерді сандық осьте салып, теңсіздікті сол аралықтарда шешеміз.
(-
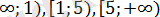
Берілген теңсіздік келесі үш теңсіздіктер жүйесінің шешімін қанағаттандырады:
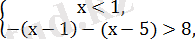
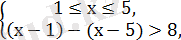
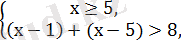
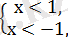
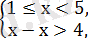
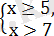
Бірінші жүйенің шешімі: х
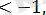 екінші жүйенің шешімі жоқ, үшінші жүйенің шешімі: х
екінші жүйенің шешімі жоқ, үшінші жүйенің шешімі: х
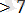
Жауабы: (-
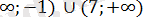
- Теңсіздікті шешіңдер: 2х+1-5
Жаңа айнымалы енгіземіз 2х+у
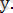 Сонда теңдеу у-5
Сонда теңдеу у-5
 2 болады.
2 болады.
Осыдан: у-5
 у-5
у-5
 -2
-2
у
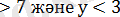
2х-1
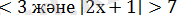
2х-1
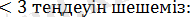
-3
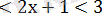
-2
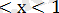
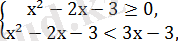
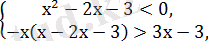
Бірінші теңсіздіктер жүйесін шешеміз:
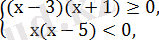
+ - + + - +
-1 3 х 0 5 х
Бірінші жүйенің шешімі: 3


Екінші жүйені шешеміз:
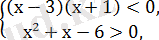
Шешімі: 2
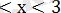
Жауабы: (2; 3)
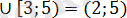
Үшінші тәсіл : у=х-2х-3 функциясының таңбалары өзгеретін нүктелерді табамыз.
Осы нүктелерді сандық осьте салып, теңсіздікті сол аралықтарда шешеміз.
2х+1
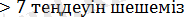
2х+1
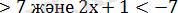
2х
және 2х
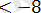
Х
және

Жауабы: (-
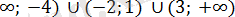
Теңсіздікті шешіңдер: 2х-3х-2
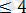
Екі теңсіздіктер жүйесін шешеміз:
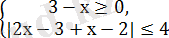
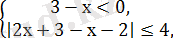
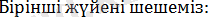
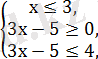
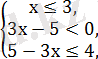
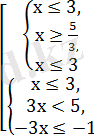

Екінші жүйені шешеміз:
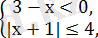
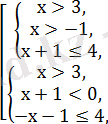
\ шешімі жоқ
шешімі жоқ
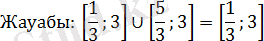
2. 4. Модуль ішіндегі айнымалысы бар теңсіздіктерді шешу
Оң санның модулі өзіне тең. Теріс санның модулі оған қарама-қарсы санға тең.
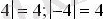
Модульдің геометриялық ағынасы:
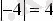
болғандықтан 0 нүктесінен -4 нүктесіне дейінгі ара қашықтық,
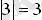 болғандықтан 0 нүктесінен 3 нүктесіне дейінгі ара қашықтық. Мысалы:
болғандықтан 0 нүктесінен 3 нүктесіне дейінгі ара қашықтық. Мысалы:
1)
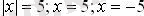
2)
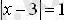 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі: х-3>0 болса, х-3= 1, х= 4; ал х-3<0 болса х-3 = -1, х = 2. Жауабы: 2; 4
Әрбір функция үшін анықталу аймақтарын, нолдерін немесе үзіліс нүктелерін табу керек. Ол нүктелер берілген теңдеудің жалпы анықталу аймағын бірнеше аймақтарға бөледі. Ары қарай
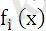 функцияларының осы аймақтардағы таңбаларын ескере отырып теңсіздікті шешеміз.
функцияларының осы аймақтардағы таңбаларын ескере отырып теңсіздікті шешеміз.
Модульмен берілген теңсіздіктерді шешу тәсілдері:
I.
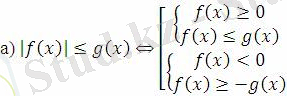
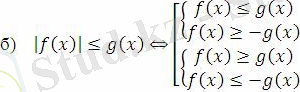
II.
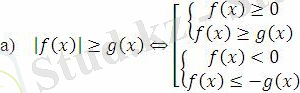
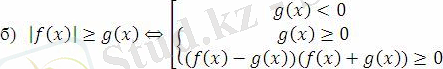

Екі айнымалысы бар сызықтық емес теңдеулер жүйесі
Екі айнымалысы бар сызықтық теңдеуде әрбір қосылғыштағы айнымалылардың дәреже көрсеткіштерінің қосындысы 1- ден артық бюлатын теңдеулер екі айнымалысы бар сызықтық емес теңдеулер деп аталады. Екі айнымалысы бар сызықтық емес теңдеудегі бірмүшелердің ең жоғарғы дәреже көрсеткіші осы теңдеудің дәрежесіболады.
Мысалы: 3х 2 + у =11 - екінші дәрежелі теңдеу;
0, 2 ху 2 - 4у 2 +1, 2 = 0 - үшінші дәрежелі теңдеу
Екі айнымалысы бар теңсіздіктер
Екі айнымалыдан тұратын теңсіздікті екі айнымалысы бар теңсіздікдеп атайды.
Функцияның анықталу облысын анықтауда сызықтық емес теңсіздіктердің жүйесін шешу тәсілдерін қолданамыз. Екі айнымалысы бар теңсіздіктерді шешу алгоритмі:
1. теңсіздікке сәйкес функция түрін анықтау
2. функция графигін координаталар жазықтығына салып, жазықтықты бөліктерге бөлу
3. жазықтықтың қай бөлігі теңсіздіктің шешімі болатынын анықтау; Ол үшін жазықтықтың бір бөлігінен кез-келген нүкте алып, оның координатасын берілген теңсіздікке қойып, дұрыстығын тексереміз; теңсіздік дұрыс болатын жазықтық бөлігінің нүетелер жиынын теңсіздіктің шешімі ретінде аламыз.
Екі айнымалысы бар теңсіздіктер жүйесін шешу
Екі айнымалысы бар теңсіздіктер жүйесінің шешуі деп жүйенің әр теңсіздігін дұрыс теңсіздікке айналдыратын айнымалының мәнін айтады. Теңсіздіктер жүйесін графиктік тәсілді қолданып шешеміз. Жүйенің шешімі теңсіздікердтің шешімдерінің ортақ бөлігі (қиылысуы) болып табылады және ол бөлік екі рет штрихталып бейнеленеді.
Теңсіздіктерді дәлелдеу
Теңсіздіктерді дәлелдеу дегеніміз - айнымалының кез-келген мәнінде теңсіздіктің орындалатынын көрсету. Теңсіздіктерді дәлелдеуде осы уақытқа дейінгі алынған білімдерді қолданып логикалық талдау жасаймыз. Мысалы:
(х+у) 2 ≥ 4ху; х 2 + 2ху+ у 2 - 4ху ≥ 0 ; х 2 - 2ху+ у 2 ≥ 0 ; (х-у) 2 ≥ 0
Яғни екі санның айырмасының квадраты барлық уақытта нөлден үлкен немесе тең болады.
Теңдеулер жүйесін қолданып есептер шығару
Есептерді теңдеулер жүйесі арқылы шығарғанда төмендегі алгоритмді қолдану керек:
1. Есептің шартын талдау
2. Берілген шамаларды әріппен белгілеу
3. Белгіленген әріптер арқылы берілген шаманы өрнектеу
4. Теңдеулер жазу және олардан жүйе құру
5. Жүйенің шешімін табу
6. Жүйе шешімдерінің қайсысы есептің берілгенін қанағаттандыратынын зерттеу
Қозғалысқа арналған есептер
Қозғалыс тақырыбында кездесетін шамалар:
Жылдамдық - v, уақыт -t, қашықтық- s
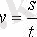
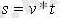
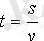
Егер қозғалыс өзен ағыстарына қатысты болса:
Сандар тізбегі және олардың берілу тәсілдері
Натурал аргументті функция санды тізбек, ал тізбекті құрайтын сандарды тізбектің мүшелері деп атайды. Жұп сандар тізбегі:2, 4, 6, 8, 10, 12, 14, 16, 18 . . . Бір ғана саннан құралған тізбек тұрақты тізбек деп аталады. Мысалы:2; 2; 2; 2; 2 . . .
Санды тізбектің берілу тәсілдері:
1) баяндау тәсілі - тізбектің орналасу заңдылығы сөзбен беріледі.
2) аналитикалық тәсіл - тізбектің n -ші мүшесі формула арқылы беріледі.
3) рекурренттік тәсіл - тізбектің (n+1) -ші мүшесі n -ші мүшесі арқылы есептелінетін формула түрінде беріледі.
Геометриялық прогрессия. Геометриялық прогрессияның n-ші мүшесінің формуласы.
Екінші мүшесінен бастап кез-келген мүшесі алдынғы мүшесін, нөлден өзгеше, қандай да бір тұрақты санға көбейткенде шығатын санды тізбекті геометриялық прогрессия деп атайды. Келесі мүшесін алу үшін алдыңғы мүшесіне көбейтілетін сан геометриялық прогрессияның еселігі деп аталады және q әрпімен белгіленеді яғни b 2 = b 1 q .
Геометриялық прогрессияның n-ші мүшесінің формуласы : b n = b 1 q n-1 .
Геометриялық прогрессияның алғашқы n мүшесінің қосындысы. Шексіз кемімелі геометриялық прогрессияның қосындысы.
Еселігі 1-ге тең емес геометриялық прогрессияның n алғашқы мүшесінің қосындысын Sn =b
1
+b
2
+b
3
+ . . . +bn деп белгілейік. Сонда:
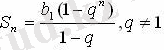 .
.
Егер q › 1 болған жағдайда, геометриялық прогрессияның n алғашқы мүшесінің қосындысын табу үшін келесі формуланы қолданған ыңғайлы:
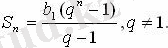
Еселігі q< 1 болатын геометриялық прогрессияны шексіз кемімелі геометриялық прогрессия деп атайды.
Шексіз кемімелі геометриялық прогрессияның қосындысының формуласы:
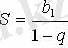
ІІІ. Модульге байланысты функция графигін тұрғызу.
Функцияның графиктерін сызу шеберлігі және оны оқи алу - математиканы игерудің негізгі элементтерінің бірі. Функцияның графиктерін салу - баланың ойлау қабілетін арттырады, білім дәрежесін барынша жетілдіреді, зерттеудің графикалық әдісін меңгеруіне, оқушылардың ғылыми негіздерін және математика курсын оқып - үйрену процесіндегі танымдық мүмкіндіктерін арттырады. Г. И. Литинский «Функции и графики» атты құралында «функциялардың графиктерін салу жоғарғы оқу орнына түсу емтихандарында болмайды деп есептелініп, орта мектепте оларға жете көңіл бөлінбейді» деп атап кетеді. Шындығында математикадан сынақтарда көптеген есептерді шешу барысында графикті салу есептің шешуін едәуір қысқартады немесе оны шешу әдісін табуға көмектеседі. Модульге байланысты функциялар графиктерін тұрғызу мектеп математика курсындағы аз қамтылған және күрделі тақырыптардың бірі. Модульге байланысты функциялардың графиктерін тұрғызудың 3 жағдайын қарастырайық: у=f х, у=f х, у=f х
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz