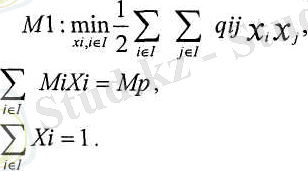Портфельдік инвестициялардың мәні және түрлері

Пән: Қаржы
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

МАЗМҮНЫ

КІРІСПЕ

1. ПОРТФЕЛЬДІК ИНВЕСТИЦИЯЛАРДЫҢ МӘНІ ЖӘНЕ ТҮРЛЕРІ

1. 1. Инвестициялық портфельдің типтері мен қалыптасу - қағидалары

1. 2. Инвестициялық портфельдің тиімділігі өлшейтін негізгі көрсеткіштер

ҚОРЫТЫНДЫ

ҚОЛДАНЫЛҒАН әДЕБИЕТТЕР ТІЗІМІ

КІРІСПЕ

Ертеде банкирлер қаржылық құжаттарды теріден жасалған дорбаларда, яғни "портфель" деп аталатынында ұстаған. Қазіргі кезде қаржылық есеп құжаттар көрінбейтін бухгалтерлік электрондық есеп айырысулар түрінде болып жатыр, ал "портфель" деген термин сақталды. Яғни, бүгінгі таңда бұл банктің барлық активтер мен пассивтердің жиынтығы дегенді білдіреді.

Портфельдік инвестициялардың мақсаты болып, инвесторлардың едәуір тиімді жұмыс істейтін кәсіпорындардың, бағалы қағаздарға және сонымен қатар мемлекеттік пен жергілікті билік органдарымен шығарылатын бағалы қағаздарға салынған қаражаттардан максималды пайда табу. Портфельдік инвестор, тікелей инвесторларға қарағанда инвестицияланатын объект - кәсіпорындарға қатысты «жақтық бақылаушыңң ұстанымына ие болады және көбінесе оны басқаруға араласпайды.

Әрі жоғары табысты, әрі жоғары сенімді, әрі жоғары ликвидті бағалы қағаздарды табу өте қиын. Әрбір бөлек қағаз ең көбі осы қасиеттердің екеуіне ғана ие бола алады. Портфельдік инвестициялаудың мэні, әртүрлі активтер топтарының арасында инвестициялық пөтенциалды тиімді бөлу болып табылады. Бастапқыда белгілі бір портфельдің қалыптасуында қандай мақсаттар мен міндеттер тұрғанына байланысты әртүрлі активтер типтерінің арасында белгілі бір пайыздық арақатынас таңдалынып, инвестордың портфель құраушылары болып келеді. Инвестордың қажеттіліктерін дұрыс ескеру және тиімді табыстылық пен мөлшерленген тәуекелді байланыстырып, активтер портфелін құрастыру -әрбір қаржылық мекемедегі менеджердің негізгі міндеті.

Сондықтан менің бұл тақырыпты тандаған себебім, портфельді басқару саласы біздің елімізде енді ғана дамып келе жатыр. Мүнда талдайтын, қарастыратын мэселелер өте көп, саланың даму барысы да қиыншылықтарға душар болуда.

Бұл тақырыптың өзектілігі де мемлекетіміздегі саланың жаңашылдығында яғни, портфельді қалыптастыруда қандай негізгі қағидалар, бағыттар және әдістер қолданатының жазып өтемін.

1. ПОРТФЕЛЬДІК ИНВЕСТИЦИЯЛАРДЫҢ ТЕОРИЯЛЫҚ НЕГІЗДЕРІ.

1. 1. Инвестициялық портфельдің типтері мен қалыптасу қағидалары.

Инвестщиялар дегеніміз капиталдың ұзақ мерзімді салымдар түріндегі қаржылық ресурстарды қолдану. Инвестицияларды заңды және жеке түлғалар жүзеге асырады, олар коммерциялық тәуекелдің дәрежесіне қарай инвесторлар: кәсіпкерлер, алып-сатарлар (спекулянттар), ойнаушыларға бөлінеді. Инвестор-эдетте қарыз (бөтен) капитал салымдарымен іске қосылып, тәуекелді минимизациялауға тырысады және сонымен қатар, ол капитал салымдарды қаржыландыруда делдал болып табылады. Кәсіпкер - ол өз капиталын белгілі бір тәуекелмен салады. Спекулянт - ол белгілі бір, алдын ала есептелген тәуекелге баруға дайын тұлға. Ойыншы - ол кез келген тәуекелге бара алатын түлға.

Инвестициялар тәуекелді (венчурлы), тіке, портфельді және аннуитетті болуы мүмкін.

Венчурлы капитал- бұл термин тәуекелді капитал салымдарды белгілеуде қолданылады. Венчурлы капитал өзара байланысты емес жобаларға салынады, яғни, жұмсалған қаражатты тез арада өтеу мақсатында.

Тікелей инвестициялар- белгілі бір шаруашылық субъектті басқаруында орын алуы мен қүдықтарға ие болу және табысты жоғарлату мақсатымен, осы шаруашылық субъектілердің жарғылық қорына салымдар болып табылады.

Портфельдік инвестициялар- портфельді қалыптастыруымен байланысты бағалы қағаздар мен басқа да активтерді сатып алу деп аталады. Портфель- салушының нақты инвестициялық мақсатқа жетудегі құрал болып, әртүрлі инвестициялық құндылықтардың біртүтас жиынтығы. Портфельге бір типті акциялар бағалы қағаздар немесе әртүрлі инвестициялық кұндылықтар (акциялар, облигациялар, жинақ пен депозиттік сертификаттар, кепілдік куәліктер, сақтандыру полистер, т. с. с. ) енуі мүмкін.

Аннуитет- бұл белгілі бір уақыт аралықтарында ақша салушыға нақты табыс әкелетін инвестициялар. Негізінен бұл сақтандыру мен зейнетақы қорларға жүмсалатын ақша салымдары.

Нарық жағдайын және инвестордың мүмкіндіктерін, оның инвестициялық стратегияны дұрыс таңдауына байланысты. Портфельдік инвестициялау басқа капитал салымдарына қарағанда бірнеше ерекшеліктер мен артықшылықтарымен көзге түседі. Инвестициялық портфель деп, заңды немесе жеке түлғаларға тиесілі бағалы қағаздардың жиынтығын айтады. Жетілген қор нарығында бағалы қағаздардың портфелі- бұл жеке басты өнім, яғни қор нарығында инвесторлардың ақша салынуында барлық қажеттілікті бүтіндей немесе бөлек қанағаттандыра алу қабілеті бар өнім. Негізінен нарықта тәуекел мен табыс арақатынасы белгіленген инвестициялық сапа сатылады және ол портфельді басқару процесінде жақсартылады/1 /.

Портфельдік инвестициялау қор нарығының әртүрлі салалардағы барлық инвестициялық қызметтердің нэтижелерін бақылауға, жоспарлауға және бағалауға мүмкіндік береді.

Портфельдік инвестициялардың негізгі міндеті- инвестициялаудың шарттарын жақсартып, бағалы қағаздардың жиынтығына бір бөлек алынған бағалы қағаз үхтанымынан ерекшелену мүмкін емес, яғни, тек қана олардың алмасуы арқылы мүмкін болатын инвестициялық сипаттама беруі болып табылады.

Тек қана портфельдің қалыптасуында жаңа белгілі сипаттамаға сай инвестициялық сапа жетіледі. Осылайша, бағалы қағаздардың портфелі инвесторларға қажетті тәуекелдің минимум дәрежедегі табыстардың тұрақтылығы қамтамасыз етілетін көмекші құрал болып келеді.

Инвестициялық портфельді қалыптасуында келесілерді ескеру қажет:

• Салымдардың кауіпсіздігі инвестициялық капиталдың нарығында келеңсіз жағдайларға инвестициялардың қарсы түрақтылығы;

• Табыс алуының тұрақтылығы;

• Салымдардың ликвидтілігі, яғни тауар алуында тез қатысу қабілеттілігі немесе тез және шығынсыз қолма қол ақшаға айналуы.

Бірақ ешбір инвестициялық құндылық аталған қасиеттерге ие болмайды, сол үшін бұл жағдайда компромиске баруға тура келеді.

Портфельді жүргізуде негізгі сүрақ болып, әртүрлі қасиеттері бар бағалы қағаздар арасында қатынасын анықтау табылады.

Портфельдік инвестициялаудың негізгі артықшылығы болып, арнайы инвестициялық міндеттерді шешу үшін портфельді таңдау мүмкіндігі табылады.

Портфельдің типі- бұл оның тәуекел мен табыс арақатынасына негізделген инвестициондық сипаттама. Сонымен қатар портфель типін сыныпталуында маңызды белгі болып, табыс қай қайнар көзінен алынған және қандай әдіспен, яғни, бағам қүнның өсуі арқылы ма, элде дивиденд пен пайыздардың ағымды төлемі арқылы ма алынғаны табылады.

Портфельдің екі негізгі типін ажыратады:

• Пайыздар мен дивидендтер арқылы алынған табысқа бағытталған (табыс портфелі) ;

• Портфельдегі инвестициялық құндылықтардың бағам құнның өсуіне бағытталған (өсу портфелі) .

Бірақ сонымен қатар өсу портфеліне әртүрлі инвестициялық қасиеттері бар түрлі түрлі бағалы қағаздар енуі мүмкін, сол үшін табыс және өсу портфелі, яғни, аралас түрі де бөлек қарастырылады.

Өсу портфелі- бағам құны өсіп жатқан компанияның акцияларынан қалыптасады. Бұл портфель типінің мақсаты- дивидендтер алуымен қатар портфельдің капиталдық құнын өсіру. Бірақ дивидендтіктөлемдер аз көлемде төленеді, сондықтан бұл топқа кіретін портфельдердің түрлерін портфельдегі акциялар жиынтығының бағамдық қүнның өсу қарқыны анықтайды.

Агрессивті өсу портфелі капиталдың максималды өсуіне бағытталған. Мүндай портфельге өсіп жатқан жас компаниялардың акциялары енеді. Осы типке инвестициялар едәуір тәуекелді болады, бірақ ең үлкен табысты экеледі.

Консервативті өсу портфелі осы топтағы портфельдер арасында ең тәуекелсіз болып келеді. Ол негізінен танымал, ірі және үлкен емес, бірақ тұрақты бағам құнның өсу қарқынымен сипатталатын компаниялардың акцияларынан тұрады. Портфельдің құрамы ұзақ мерзімде тұрақты қалып, капиталдың сақталуы үшін бағытталған.

Орташа өсу портфелі агрессивті және консервативті портфельдердің қасиеттерін біріктіреді. Яғни түрақтылығы мен сенімділігі консервативті өсуімен, ал табыстылығы агрессивті өсуімен қамтамасыз етіледі.

Табыс портфелі пайыздық және дивидендтік төлемдердің ағымды табыстың максималды көлемін алуына бағытталған. Бұл портфель типінің ерекшелігі болып, консервативті инвестор үшін тиімді келетін минималды тәуекел дәрежесіне сәйкес келетін табыс деңгейінің қажетті көлемін алу мақсаты табылады.

Теракты табыс портфелі жоғары сенімді бағалы қағаздардан қалыптасып, минималды тәуекел деңгейінде орташа табыс экеледі.

Табысты қағаздар портфелі орташа тәуекел деңгейінде жоғары табыс экеледі және жоғары табысты корпорациялардың облигациялардан, бағалы қағаздардан тұрады.

Табыс және өсу портфелінің құрылуы қор нарығындағы бағамның төмендеуі мен темен дивидендтік және пайыздық төлемдерден болатын жоғалтулардан сақтану үшін қолданылады. Қаржылық активтердің бір бөлігі оның иесіне капитал құнның өсуін әкелсе, екінші бөлігі табыс әкеледі.

Екі бағытты портфельдің қүрамына салынған капиталдың өсуі жағдайында оның иесіне жоғарғы табыс экеледі. Яғни, бұл екі типті акцияларды шығаратын компаниялардың бағалы қағаздарға капитал салу, бірінші типі жоғарғы табыс әкелсе, екіншісі капиталдың өсімін қамтамасыз етеді.

Балансталған портфель тек қана табысты балансталмай, сонымен қатар бағалы қағаздармен операцияларды жүзеге асыру барысында болатын тәуекелді де балансқа келтіреді/2/.

Инвестициялық портфельді құрастырғанда келесідей қағидалар қолданылады:

• Консерватизм қағидасы, жоғары сенімді және тәуекелді бөлімдер арақатынасы бір-бірін орын басу арқылы құрылады. Осылайша, инвестициялық тәуекел негізгі сомманы жоғалтуында емес, жеткіліксіз жоғары табыс алуында болады;

• Диверсификация қағидасы, бұл портфельдік инвестициялаудың бастысы болып келеді. Бұл қағиданың негізгі идеясы ағылшын мақалынан шығады-бір дорбаға барлық жүмыртқаларды салмаңыз. Яғни, барлық қаржыны бір түрлі бағалы қағазға салмау қағидасы, осы арқылы көптеген жоғалтулардан өз-өзін сақтай аласыз;

• Жеткілікті ликвидтілік қағидасы, портфельдегі тез сатылатын активтердің үлесін жоғары табысты мэмілелерді жүзеге асыру үшін қажетті деңгейде ұстау және клиенттердің ақша қаражатындағы қажеттілікті қанағаттандыра алатын деңгейді тұрақты жағдайда ұстау.

1. 2 Инвестициялық портфельдің тиімділігін өлшейтін негізгі қөрсеткіштер.

Пайда табу мақсатында, инвестор әртүрлі тэукелдерден қорғанып қаржы құралдарын портфелін қалыптастыру керек. Портфель тәуекелдерін басқарудың екі негізгі әдісі бар. Бөлек қаржы құралдарына немесе олардың тобына қатысты тәуекелдер (жүйелі емес тәуекелдер), инвестициялық портфельді диверсификациялау арқылы төмендетуге болады. Ал, бөлек қаржы құралдарын тәуекелдері өзара өте корреляцияланған болса (жүйелі тәуекелдер), диверсификация тек тәуекелдердің орташа мэнге келтіреді.

Жүйелі тәуекелден қорғану үшін, портфельді тәуекелдің кез-келген факторға сезімталдығы жоқ болатындай құрастыру қажет. Тәуекелді басқарудағы мүндай бағыт хеджирование немесе иммунизация деп аталады.

Қазіргі қаржылық құралдарың түрлері өте көп. Портфельді құрастыруда тәуекел факторлармен қоса, инвестор операцияларды жүргізу үшін биржалық шектеулерді, салық салу және реттеуші органадрының шектеулерін ескеру тиіс. Мүндай жағдайларда портфельді қалыптастыру міндеті өте ауыр және еңбекті көп қажет етеді. Оны шешуге қажетті аппарат математикалық бағдармалау әдістер жиынтығы түрінде болады.

Жүйелі емес тәуекел, яғни бөлек қаржы құралдарға қатысты тәуекел портфельді диверсификациялауға қосымша шектеулердің көмегімен қадағаланып отырды. Жүйелі емес тәуекелдерді басқаруда кең жайылған бағыттарының бірі орташа табыстылық және табыстылық дисперсияның (mean- variance analysis) портфель сипаттамаларын бейнелеуіне негізделеді.

Оптималды портфель болып, берілген дисперсия деңгейіндегі жоғарғы табыстылыққа және берілген тәуекел деңгейіндегі төмен табыстылық дисперсиясына ие табылады. Портфель құраушылары тұрақты табыстылығы бар кұралдар және акциялар болуы мүмкін. Қарастырып жатқан портфельдің оптимизациялау, бағытының негіз қалаушысы, нобель лауреаты Г. Марковиц болады/3/.

Оптимизациялық есептің сәйкес өрнегін жазу үшін келесі белгілерді енгізейік:

Q - қаржы құралдардың табыстылықтары арасындағы ковариациялар матрицасы, {qy}, i, j si;

Mi - і-ші қаржылық құралдың күтілетін табыстылығы, і ε I;

Mp - талап етілетін портфельдің орташа табыстылығы;

Хі - і-ші типтегі құралдардан тұратын, портфельдің үлесі, і ε І.

Шексіз қарызға алушылық рұқсат етілген жағдайда портфельдің қалыптасуы, келесі оптимизациялық есепті шешу арқылы жүзеге асады:

Оптимизациялаудың критерии болып, портфельдің табыстылық дисперсиясы табылады. Ml есептің шешім оптималдылығының бірінші деңгеши" шарттарын қолданудың аналитикалық жолымен табуға болады /4/:

мүнда

е - барлық құраушылар бірге тең, вектор;

М - қаржы құралдар табыстылығының математикалық күтулердің векторы, М=(М ₁ М ₂ , . . . , М _j ) ^Т ; φ, W-M1 есебінің шектеулеріне сәйкес Лагранж көбейткіштері.

Егер де қаржы құралдарының қысқа сатылымдарына тиым салынса, онда Ml есебінде Х>0, і е I шектеулер қосылады. Бұл жағдайда оптимизациялық есептің шешімі үшін сандық әдістер қолданылады.

Мр әртүрлі мэндерінде есептің шешімі белгілі бір орташа табыстылық пен табыстылық дисперсиясымен сипатталынатын портфельдер жиынтығын береді. Егер оптимизацияланған портфельдер үшін орташа табыстылық пен

табыстылықтың орташа квадратты ауытқуының Sp арасында тэуелділікті 1 суреттегі қисық арқылы корсете аламыз.

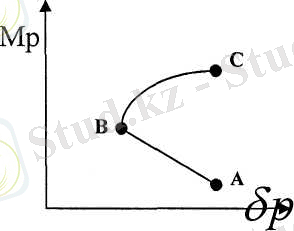
1 Сурет. Портфельдердің тиімді жиынтығы.

АВ қисығының кесіндісінде нүкте ретінде көрсетілген әрбір портфель үшін ВС кесіндідегі сәйкес келетін орташа квадраттық ауытқу мен жоғары орташа табыстылығына ие портфель бар болады. Осылайша ВС қысығының кесіндісі ең жақсы портфельдер жиынтығы, яғни тиімді жиынтығынан портфельді таңдау инвестордың тәуекелге қатынасымен анықталады. Осыны анықтау үшін талғамсыздық қисықтары (indifference curves) пайдаланылады. (сурет 2) .

Бір қисықтың үстінде орналасқан барлық портфельдер инвесторды бірдей қанағаттандырады. Инвестор бір-біріне параллель шексіз көп талғамсыздық қисықтарына ие болады. Егер де талғмасыздық қисықтарыдөңес болса, инвестор орташа табыстылық жоғарласа ғана тәуекелдігін жоғарлатуға барады. Мүндай инвесторды тәуекелге икемсіз деп атайды (risk-averse) /15/.

Тиімді жиынтығынан ең жағымды портфельді таңдап алу үшін инвестор өз талғамсыздық қисықтарын тиімді жиынтық қисығымен бірге бір графикте бейнелеу тиіс.

Ең жағымды портфель талғамсыздық қисығы мен тиімді жиынтық қисығы қиылысу нүктесі орналасады. (суретЗ)

Мр Мр

Тәуекелсіз қаржы құралдары бар болғанда қарастырған есебіміз жеңілденеді. Бюджеттік шектеуді 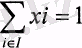жоюға болады, өйткені қалған

қаражаттар тәуекелсіз құралдарға инвестицияланады. Онда, оптимизациялық есеп келесі түрге ие болады:

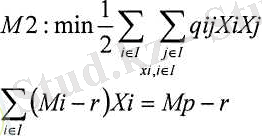
мұнда

г - тәуекелсіз құралдың табыстылығы.

М2 - есебінің аналитикалық шешімі келесідей жазылады:

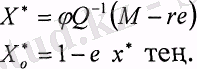; тәуекелсіз құралдарға ивестициялардың көлемі.

Ml және М2 оптимизациялық модельдерінің 2 негізгі шектеуді атап өтейік. Екі модельде жүйелі емес тәуекелді қадағалайды және жүйелік тәуекелді ескермейді. Егерде нарық индексіне і-ші қаржы құралдың р; регрессиялық коэффициентін қарастырсақ, онда портфельдің нарықтық тәуекелі қосымша шартты енгізу арқылы шектелуі мүмкін:

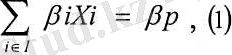
мұнда

Рр- нарық индексіне барлық портфельдің талап етілетін регрессия коэффициентінің шамасы.

Ml және М2 модельдері акцияларға қолданылып, опциондарға қолданыла алмайды. Сызықты емес құралдар портфельдерінің оптимизациясы жиі пайдалылық функциясын қолдану арқылы жүзеге асады.

Егерде талғамды қалыптастыру үшін кездейсоқ шамалар туралы сөз болса, онда күтілетін пайдалылық (expected и1іШу) концепциясы пайдаланылады. Бұл теорияның іргетасын қалағандар америка ғалымдары фон Нейман және Моргенштерн /5/ б. т.

Инвестордың қалауы бұл концепцияның шегінде орналасқан, егер u функциясы бар болып, 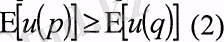р және q кездейсоқ шамалар үшін келесі теңсіздік,

р - кездейсоқ шама инвестор үшін q кездейсоқ шамадан жаман емес болған жағдайда ғана орындалады (Е- математикалық күту) .

R - алынатын пайданы анықтайтын кездейсоқ шамалардың жиынтығы болсын. Пайдалылық теориясында инвестордың бір кездейсоқ шаманы екінші кездейсок шамадан қалғанын ">" белгі арқылы көрсетеді, 'V белгі қатаң талғамды білдіреді. Кездейсоқ шамалардың эквиваленттілігі "«" белгімен көресетіледі. Егер р > q және q > г -ден р > г дегені шықса, талғамдардың қатынасы транзитивті деп аталады. Ал, егер кез-келген екі р және q бөлулері үшін ^>^және q>р теңсіздіктер орын алса, талғамдар қатынасы толық деп аталады.

Басқа кең тараған пайдалылық функциясы - экспонентті:

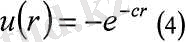
мүнда с> 0 (сурет 5)

1960 ж. Грейсон кәсіпкерлердің пайдалылық функциясын қайта қалпына келтіру түрлі зерттеулерді жариялаған. Осы зерттеулерде инвесторлардың талғамдары көп жағдайларда логарифмдік пайдалылық функциясымен жақсы сипатталатының дэлелдеді. (сурет 6)

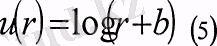
мүнда r >-b

р кездейсоқ шаманың математикалық күтуді /?арқылы белгілейік. Пайдалылық теориясында, егер инвестор /жездейсоқ шамамен сипатталынатын лөтерея ұтысынан, кепілдігінен р ұтысын таңдаса, тәуекелге икемсіз (risk-averse) деп аталады. Демек келесі теңсіздік шығады:

Тәуекелге икемсіз инвестордың пайдалылық функциясы ойыс (concave) екенін дэлелдеген. Егер инвестор тәуекелге икемді болса, оның пайдалылық функциясы дөңес (convex) болады. Квадраттық, экспонентті және логарифмдік функциялар ойыс, демек тәуекелге икемсіз инвестордың талғамдарын көрсетеді.

Р кездейсоқ шамаға үтысы тең лөтереяның детерминант эквивалент

болып, инвестордың лөтереядағы қатысуы мен р алу арасындағы талғамынаталғамсыз болатын ршамасы табылады. />шамасы и\ р \ = Щи{р) \ теңдікпен анықталады немесе

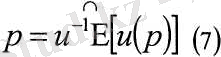
Лөтереядағы күтілетін үлысы мен оның детерминант эквивалент арасындағы айырмашылық тәуекел қосымша деп аталады:

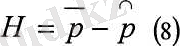
Пайдалылық функциясының маңызды сипаттамасы болып, тәуекелге жергілікті бейімсіздігі болып табылады, ол келесі түрге ие:

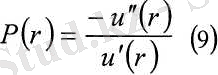
Квадраттық пайдалылық функция үшін тәуекелге жергілікті биімсіздігі келесідей болады:

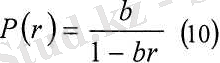
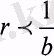болғанда, Р ең және өспелі функция болып табылады.

Инвестордың талғамдарын күтілетін пайдалылықтың көмегімен көрсету үшін Фон Нейман мен Моргенштерн 3 аксиоманы қажетті және жеткілікті шарт деп есептеді:

R-дағы барлық кездейсоқ шамалар бірдей мэндер жиынтығында анықталсын.

Аксиома 1. ">" қатынасы транзитивті және толық болып табылады.

Аксиома 2. 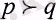-дағы барлық 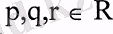және ае (ОД) -ден

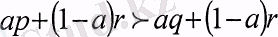шығады.

Мұндағы мәндер мүмкін бөліністердің қоспасы болып келеді. Мысалы, 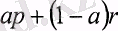кездейсоқ шама келесідей шығарылады, бастапқыда екі нәтижесі бар, мүмкіндіктері а және 1-а тең тэжірибе өткізіледі. Бірінші нэтижеде р кездейсоқ шама генерацияланады, ал екіншіде- q кездейсоқ шама. Осы аксиоманы тәуелсіздік аксиома деп аталады. Оның мэні 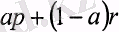және

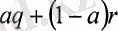кездейсоқ шамалар арасындағы инвестордың таңдауы оның р және q кездейсоқ шамалар арасындағы таңдауына қатынасымен анықталады.

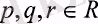АксиомаЗ. Егер болғанда, барлық үшін

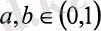
болса, онда 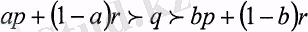болады. Бұл Архимед аксиомасы деп

аталады. Осы аксиома бойынша р кездейсоқ шама қаншалықты «жақсың болғанмен кез-келге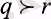н үшін 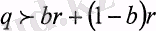болатындай ең кішкентай в

ықтималдық табылады. Басқа жағынан да г кездейсоқ шама қаншалықты «жаманң болса да, кез-келге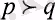н үшін 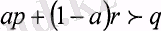орындалатындай а

үлкен ықтималдық табылады. Күтілетін пайда негізінде инвестордың талғамдарын көрсету үшін эдетте бірнеше функциялар қолданылады. Олардың қатарына квадраттық функция жатады: (сурет 4)

(\ ^brl

W) = r-z- , (з)

мұнда

r- табыстылық.

Квадраттық функция г -< - шартымен қарастырылады, өйткені бұл

шарттың шектерінен асқан жағдайда квадраттық функция r-дің өсуімен кемиді. Ml және М2 модельдері квадраттық пайдалылық функциясымен іс әрекетін бейнелейді/33/.

Экспонентті пайдалылық функция үшін:

Тәуекелге жергілікті бейімсіздігі тұрақты және оң, өйткені с у О Логарифмдік пайдалылық функция жағдайында:

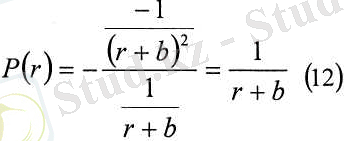
болғандықтан, барлық г үшін 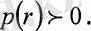Қарастырылған пайдалылық функция тәуекелге төмендейтін икемсіздігі бар инвесторды сипаттайды.

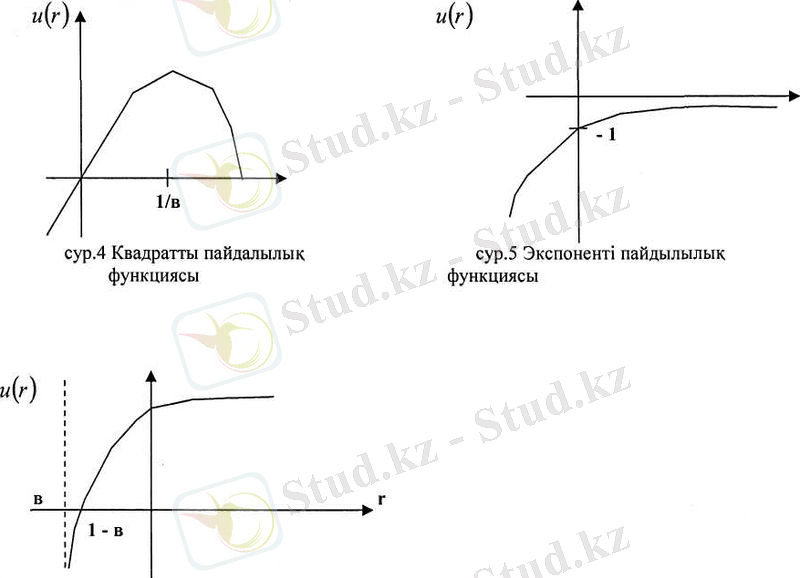
сур. 6 Логарифмдік пайдалылык функциясы

Жоғары айтылғандай, күтілетін табыстылық пен табыстылық дисперсиясымен қызмет ететін оптимизация модельдері опциондық мэмілелері бар портфельдер үшін қолданыс таппайды. Карино және Тернер еңбегінде келесі пайдалылық функцияны үсынады, оның математикалық күтуі портфельдің оптимизация критерийі ретінде пайдалана алады. WT _max арқылы соңғы қарастырылған уақыт аралығындағы портфельдің қүнын

белгілейік, модельдің авторлары портфельді басқару нәтижесінде мүмкін пайда болатын жағымсыз эффектерді (embarrassments) қарастырады. Mr деп, r-лік жағымсыз эффектен зиянды сипаттайтын кездейсоқ шаманы белгілейік.

- г-ші жағымсыз эффекпен байланысты залалдың қүның анықтайтын 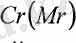дөңес функция болсын /6/ еңбекте үсынылатын пайдалылық функция келесідей:

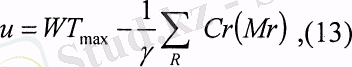мүнда

у - инвестордың тәуекелге икемсіздігін көрсететін

коэффициент.

Пайдалылық функцияның қолдануымен байланыссыз фьючерстер мен опциондар портфельдерді басқару бағытты 111 қарастырылады. Оптимизацияның критериі болып, ең жақын опциондық төлемдер мерзімінде портфель табыстылығының максимум математикалық күтуі қолданылады. Жұмыста базистік актив бағасының мэндер ықтималдықтар бөлу логнормалдық моделі пайдаланылады. Осыған байланысты берілген интервал ретінде базистік актив баға логарифманың -З^және +3S салыстырмалы болжамды мэндер координатасы бар мәндердің кесіндісі таңдалынады.

Ill қарастырылатын оптимизациялық модель нақты уақыт тәртібіндегі туынды қаржы құралдардың биржалық портфелін басқару үшін арналған. Сонымен қатар қаржылық құралдардың сату мен сатып алу бағаларының айырмашылығы және операциялар жүзеге асқан кездегі брокермен алынатын комиссия ескеріледі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.