Синусоидалы тоқтар

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

« Инженерлік экономикалық»факультеті

КУРСТЫҚ ЖҰМЫС

Тақырыбы : «Синусоидалы тоқтар»

Мазмұны

I. Кіріспе . . . 3

II. Негізгі бөлім

1. Екіполюстіктер мен төртполюстіктерге жалпы түсініктеме . . . 4-5

1. 1 Синусоидтық ток тізбегіндегі екіполюстіктер . . . 5-6

2. Екіполюстіктің резонанстық режим жұмысы . . . 6

3. Төтрполюстіктер . . . 6-7

3. 1 Синусоидтық токтар кезіндегі төртполюстіктердің теңдеулері . . . 7-8

3. 2 Төртполюстіктердің коэффициенттері . . . 8-9

3. 3 Төртполюстіктердің жүктелу режимі . . . 9

4. Көпполюстіктер . . . 10-11

5. Есептің берілгені . . . 11

6. Есептің берілген схемалары . . . 12

7. Осциллографтағы схемалардың көрсетуі . . . 13

8. Жиілікті екі еселенген кездегі осциллографтағы көрсетуі . . . 14

III. Қорытынды . . . 15

9. Қолданылған әдебиеттер …… . . . 16

КІРІСПЕ

Электротехниканың дамудың басталуы

XXI ғасырдың бірінші жартысында электротехника дами бастады. Электр токтың ашылуы мен оның қасиеттерін зерттеу XXI ғасырға жатқызамыз. Ол кезде, яғни 1799 жылы А. Вольт бірінші болып электрохимиялық тұрақты ток көзін ашқан болатын. XXI ғасырдың бірінші жартысында көптеген елдердің ғалымдардың зерттеулерінің арқасында, соның ішінде көрнекті орын алатын орыс академигі В. В. Петров, токтың химикалық, жылулық, жарықтық әсерлерін ашты. 1825- 1827 жылы А. М. Ампер өз жұмыстарын жарыққа шығарды, сол жұмыстары электродинамиканың ашылуына үлкен ықпал тигізді. Сонымен бірге, ол «электр ток» терминін бірінші болып ұсынған. 1827 жылы Г. С. Ом электр тізбектер үшін заң ашты және сол заңдар оның атымен аталды.

1845-1847 жылы ашылған Кирхгоф заңдары электр тізбектер анализі үшін және сонымен қатар, 1853 жылы эквивалентті активті екіполюстіктер теоремасы маңызды рөлге ие болды. XXI ғасырдың бірінші жартысында сенімді экономды генератордың болмауының әсерінен, электр энергияны пайдалану мүмкіндіктері болмады. Сол кезде тұрақты электр көзі ретінде көбінесе гальвани батареяларын қолданды. Гальвани батареялары өте үлкен болды, ал олардың электр қозғаушы күштердің әсерінен уақыт сайын поляризация құбылысы азая берді.

1880 жылы Д. А. Лачинов пен 1882 жылы М. Депренің теориялық зетрттеулері бойынша кернеудің жоғарлануы үлкен қашықтықтағы электроэнергияның экономды берудің жоғарлауына әкеп соғады. Бірақ, сол кезде аса жоғарғы генераторларды жасауға мүмкіндіктер болған жоқ. Басты қиыншылық- тұрақты токтың трансформациясының мүмкін болмауында болды. Сондықтан, электрмен қамтамассыз ету үшін, көптеген ғалымдар айнымалы токтың пайдаланудың мүмкіндіктерін зерттеді.

Екіполюстіктер мен төртполюстіктерге жалпы түсініктеме

Электр тізбектерді, эквивалентті генератордың өз электр қозғаушы күшімен және оның ішкі кедергісімен ауыстырған кезде, екіполюстіктер пайда болады. Өйткені, оның арасымен қабылдағыштың арасында тек ғана екі полюс- А және В бар. Пассивті екіполюстіктер деп, оның ішінде энергия көздері жоқ болса, ал активті, егер оның ішінде энергия көздері бар болғанды айтады. Екіполюстіктерді жалпы бір параметр бойынша айтқанда, кіретін кедергімен немесе кіретін өтімділікпен сипатталады.

Бірақ, практикада ток көзімен(кіріс) қабылдағыштың (шығыс) арасында әр түрлі байланысты күрделі болуына ықпал ететін схемалар болады. Осындай схемаларды, яғни екі кірісі және екі шығысы бар қысқыштарды төртполюстіктер деп атайды. Күрделі электр тізбектерінің режимін зерттей отырып, токтардың, кернеулердің және қуаттылықтардың әр түрлі учаскілер мен бұтақтар арасындағы байланысқа әкеледі. Сол режим бойынша басқа тізбектердегі ток белгісіз болуы да мүмкін бірақ, сонымен де оның барлық параметрлері есептің шешілу кезінде есептелінеді. Осы шарттарда қарастырылатын тізбек тиісті қысқыстардың параметрлері бойынша анықталады. Қысқыштардың потенциалдар мен токтардың байланысуының арасында керекті және жеткілікті жалпы параметрлерді анықтайтын тізбектің жартысын көпполюстіктер деп атайды. Көпполюстіктердің полюс саны тіктөртбұрыштың қысқыш полюстерінің санына сәйкес болған түрінде суреттеледі.

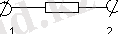
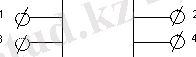
1) суретте пассивті екіполюстіктер;

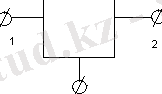
2) суретте үшполюстіктер;

3) суретте төртполюстіктер;

Көптеген электр құрылғылар, энергияны немесе сигналдарды беру үшін қолданылатын, екі кіретін және екі шығатын қысқыштардан тұрады. Сонымен қатар, олардың ішкі электр өткізгіші өте күрделі болғанда, осы құрылғыларды пассивті- төртполюстіктер , егер ішінде энергия көздері болмаған кезде, ал активті- төртполюстіктер деп, егер ішінде энергия көздері бар болғанды айтады. Енді пассивті- төртполюстіктерді қарастырайық, барлық төртполюстіктердің элементтерінің параметрлерін тұрақты деп аламыз.

Атап өтейік, сызықты пассивті- екіполюстіктер, сонымен қатар, сызықты пассивті- төртполюстіктер жалпы жағдайда өздерінің ішінде энергия көздері бар болады, бірақ олар міндетті түрде, бір-бірін толықтыру, яғни компенсациялауы тиіс. Сонымен қатар, олардың кіру кернеулері екіполюстіктер мен төртполюстіктер үшін ашу қысқыштарында 0-ге тең.

Пассивті- төртполюстіктерге мысал келтірсек, трансформатор, электр фильтр. Олар екі кіретін (1, 1’) және екі шығатын (2, 2’) қысқыштардан тұрады.

Синусоидтық ток тізбегіндегі екіполюстіктер

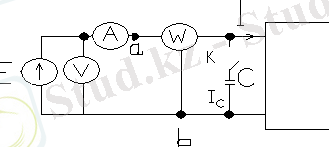
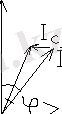
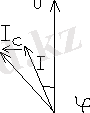
а) б) в)

Екіполюстіктің кіріс кедергісін анықтаған кезде суреттегі а) схемасын пайдаланамыз. Кірістегі кернеу U _ab =U. Ваттметр Re{U _ab I} өлшейді, яғни активті қуаттылықты P=UIcos φ. Кірістегі кедергінің модулі z=U/I;

cos φ= P/UI.

Косинус бұрыш арқылы sin φ табады, содан кейін R _ax =z cos φ,

X _ax =z sin φ табады. Косинус жұп функция болғандықтан cos(-φ) = cos φ, өлшемін тағы бір тәжірибемен толықтыру керек. φ бұрышын анықтау үшін фазометр құралы қолданылады. Екіполюстікке параллельді түрде К тұйықталу кілтіне кішкентай С сыйымдылықты қосамыз. а) суретінде; Егер амперметр бойынша К тұйықталу кілтінің көрсетуі азайса, тұйықталмаған кілт кезге қарағанда, онда φ бұрышы оң және кіріс кедергісі Z=ze ^iφ индуктивті қасиетке ие. б) суретінде; Ал егер амперметр бойынша К тұйықталу кілтінің көрсетуі артса, тұйықталмаған кілт кезге қарағанда, онда φ бұрышы теріс және кіріс кедергісі сыйымдылық қасиетке ие болады. в) суретінде; Векторлы диаграммаларда б), в) суреттеріндегі I- екіполюстік арқылы өтетін ток; I _C - сыйымдылық арқылы өтетін ток; Пунктирлы сызықтар, тұйықталған кілт кезіндегі амперметр арқылы өтетін ток;

Екіполюстіктің резонанстық режим жұмысы

Екіполюстік бір немесе бірнеше индуктивті элементтер мен бір немесе бірнеше конденсаторлар бар болсын. Сыртқы тізбекке қарағанда, екіполюстіктер резонанстық режимде өзін активті кедергі ретінде ұстайды, сондықтан ток және кернеу, оның кірісінде фаза бойынша сәйкес келеді. Екіполюстіктердің реактивті қуаттылығы онда 0-ге тең. Резонанстық режимнің екі негізгі түрі бар: ток резонансы және кернеу резонансы.

Төтрполюстіктер

Электр фильтр, трансформаторлар, транзисторлар және электр энергиясын беру сызықтарын төртполюстіктер түрінде қарастырғанда өте ыңғайлы болып келеді. Төртполюстіктер, екіполюстіктер сияқты сызықты немесе сызықты емес, активті немесе пассивті бола алады. Енді пассивті, сызықты төртполюстіктердің қасиеттерін қарастырайық. Энергия көзіне қосылатын төртполюстіктің екі қысқыштарын- кіріс, ал қабылдағышқа қосылатын- шығыс деп аталады. Төртполюстіктің кіріс кернеуінің шығыс кернеуінің қатынасын U ₂ / U ₁ , K _u кернеудің беру коэффициенті деп атайды. Осылай токтардың қатынастарын да I ₂ /I ₁ , K _I токтардың беру коэффициенті деп атайды. Төртполюстіктердегі негізгі есептің анализі, ол кіріс кезіндегі кернеу мен токты U ₁ , I ₁ және шығыс кезінде U ₂ , I ₂ өз арасында байланыстыру.

U ₁ = h ₁₁ I ₁ + h ₁₂ U ₂

I ₂ = h ₂₁ I ₁ + h ₂₂ U ₂

Осы теңдеуді h-параметрлердегі төртполюстіктер теңдеуі деп атайды. h ₁₁ , h ₁₂ , h ₂₁ , h ₂₂ комплексті коэффициенттерді шығару арқылы немесе төртполюстіктің кез-келген екі режим арқылы экспериментті жолмен алуға болады. Кірісте қысқа тұйықталу (U ₂ =0) және шығыста холостой ход кезінде (I ₁ =0) :

h ₁₁ =(U ₁ /I ₁ ) _U2=0 - шығыстағы қысқа қысқыштардың кіріс кедергісі;

h ₁₂ =(U ₁ /U ₂ ) _I1=0 - кіріс кезіндегі тұйықталмаған қысқыштардың беру кернеуінің кері коэффициенті, оны кернеу бойынша кері коэффициентінің байланысы деп атайды;

h ₂₁ =(I ₂ /I ₁ ) _U2=0 - шығыстағы қысқа қысқыштардың токты беру коэффициенті;

h ₂₂ =(I ₂ /U ₁ ) _I1=0 - кірістегі тұйықталмаған қысқыштар кезіндегі шығыс өтімділігі;

Синусоидтық токтар кезіндегі төртполюстіктердің теңдеулері.

Синусоидтық токтар кезінде комплексті кедергімен жұмыс істейміз. Бірақ барлық заңдылықтар сол түрінде қала береді. Ескерту! Схемада ішкі қосылуы төртполюстіктерде және комплексті кедергінің мәндері өзгермейді, ал жүктелу (нагрузка) және кіріс кернеуі өзгере алады.

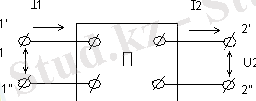
Осы схемада пассивті төртполюстіктер көрсетілген. U ₁ , I ₁ өзгеретін мәндер. Солар арқылы екі белгісіз мәндерді табуға болады және осы теңдеулердің алты түрлері (формалары) бар.

А-форма Y- форма Z- форма

U ₁ =AU ₂ +BI ₂ I ₁ =Y ₁₁ U ₁ +Y ₁₂ U ₂ U ₁ =Z ₁₁ I ₁ +Z ₁₂ I ₁

I ₁ =CU ₂ +DI ₂  I ₂ =Y ₂₁ U ₁ +Y ₂₂ U ₂ U ₂ =Z ₂₁ I ₁ +Z ₂₂ I ₂

H-форма G-форма B-форма

U ₁ =H ₁₁ I ₁ +H ₁₂ U ₂ I ₁ =G ₁₁ U ₁ +G ₁₂ I ₂ U ₂ =B ₁₁ U ₁ +B ₁₂ I ₁

I ₂ =H ₂₁ I ₁ +H ₂₂ U ₂ U ₂ =G ₂₁ U ₁ +G ₂₂ I ₂ I ₂ =B ₂₁ U ₁ +B ₂₂ I ₁

Негізгі А - формасы болады.

Төртполюстіктердің коэффициенттері

A, B, C, D коэффициенттері осы теңдеу бойынша 1+ R _ab /R _bc =A; R _ab =B; 1/R _ca +1/R _bc *R _ca +1/R _bc =C; 1+R _ab /R _bc =D; схемадағы төртполюстіктер ішінде қосылуына байланысты. X _L және X _C кедергілердің мәндері, сонымен бірге, олар жиілікке тәуелді.

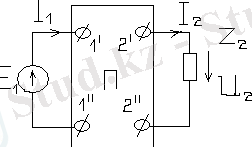
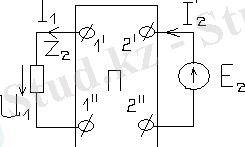
AD-BC=1; U ₁ ~E ₁ , U ₂ ~E ₂ ; I ₁ және I ₂ контурлы токтар болып табылады. Сонымен, контурлы токтар теңдеуін құруға болады.

I ₁ =U ₁ Y ₁₁ -U ₂ Y ₁₂ 1)

I ₂ =U ₁ Y ₂₁ -U ₂ Y ₂₂

сызықты төртполюстіктерде Y ₁₂ =Y ₂₁ . Сонда

U ₁ =I ₂ +U ₂ Y ₂₂ /Y ₂₁ =U ₂ Y ₂₂ /Y ₂₁ +I ₂ 1/Y ₂₁

енді 1-ші теңдеуге қоямыз.

I ₁ =(U ₂ Y ₂₂ /Y ₂₁ +I ₂ 1/Y ₂₁ ) Y ₁₁ -U ₂ Y ₁₂

немесе

I ₁ =U ₂ (Y ₂₂ Y ₁₁ - Y ₁₂ Y ₂₁ /Y ₂₁ ) +I ₂ Y ₁₁ /Y ₂₁ ; 2)

Y ₂₂ /Y ₁₁ =A; 1/Y ₂₁ =B;

(Y ₁₁ Y ₂₂ -Y ₁₂ Y ₂₁ ) /Y ₂₁ =C;

Y ₁₁ /Y ₂₁ =D; 3)

Осыдан, U ₁ =AU ₂ +BI ₂

I ₁ =CU ₂ +DI ₂

сонымен, А- форма түріндегі төртполюстіктер теңдеуі шықты. 3-ші теңдеуді пайдалана отырып, комплексті коэффициенттердің мәнін табуға болады. Коэффициенттердің өлшемдері тұрақты ток кезіндегідей. B- формадағы коэффициентті энергияны қайта беру кезінде А-форма коэффициенті арқылы көрсетуге болады. Сонда теңдеу мынандай түрге ие болады:

U ₂ =DU ₁ +BI ^’ ₁

I ^’ ₂ =CU ₁ +AI ^‘ ₁

Төртполюстіктердің жүктелу режимі

Берілген U ₂ және I ₂ тәжірибедегі қысқа тұйықталу осы қатынас шықты:

U _1K =AU ₂ ; I _1K =CU ₂ ; U _1K =BI ₂ ; I _1K =DI ₂ ;

U ₁ =AU ₂ + BI ₂ осыған қоямыз.

I ₁ =CU ₂ +DI ₂

U ₁ =AU ₂ +BI ₂ = U _1K + U _1K

I ₁ =CU ₂ +DI ₂ =I _1K +I _1K,

сонымен U ₁ кернеу мен I ₁ кедергі кез-келген берілген приемниктің жұмыс режимінде барлық параметрлерінің қосындысына тең.

Көпполюстіктер

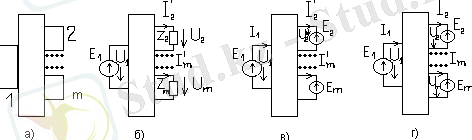
а) суретінде пассивті схема бейнеленген, оның m бұтақтары бар. Осы схемада көпполюстіктер көрсетілген. Кірістегі y ₁₁ , y _mm және y _rm y _mr бұтақтардың өтімділігі де бізге мәлім дейік. r-контур, барлық контурлы токтардың бағыттары бірдей, контурлы токтар әдістер бойынша. 1-ші бұтақты қосайық, E ₁ =U ₁ , ал 2-m бұтағында Z ₂ -Z _m жүктелу болып табылады. 2-m бұтағын I ₂ ^’ -I _m ^’ , ал 1- ші бұтақты I ₁ деп белгілейік. Барлық токтардың бағыттары сағат тілінің бағытымен сәйкес келеді. Компенсация теореманың негізінде Z ₂ -Z _m жүктеуді э. қ. к -нің көзіне E ₂ -E _m , I ₂ ^’ -I _m ^’ токтарға қарама-қарсы бағытталған. Беттестіру әдісінің приципі бойынша ток бұтақтарына келесідей теңдеу жазамыз:

I ₁ =U ₁ y ₁₁ -U ₂ y ₁₂ -U ₃ y ₁₃ - _… -U _m y _1m ,

I ₂ ^’ =U ₁ y ₂₁ -U ₂ y ₂₂ -U ₃ y ₂₃ -…U _m y _2m ,

. а)

I _m ^’ = U ₁ y _m1 -U ₂ y _m2 -U ₃ y _m3 -…-U _m y _mm .

2-m бұтағындағы ток бағытын қарама-қарсы бағытқа өзгертейік және оларды I ₂ -I _m (I ₂ =-I ₂ ^‘ , …, I _m =-I _m ^‘ ) деп атаймыз. (г- суреті) ; Барлық теңдеудегі қосындылар оң болу үшін Y _KK =y _KK деп белгілеп, аламыз.

Y _1K =-y _1K =-y _K1 ; Y _PR =Y _RP =y _PR =y _RP (p≠r≠1) .

Онда көпполюстіктер осындай түрге ие болады: [Y] [U] =[I] ;

Y ₁₁ Y ₁₂ Y ₁₃ . . . Y _1m U ₁ I ₁

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.