Кирхгоф заңдары

Пән: Электротехника
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

РЕФЕРАТ Астана қаласы
Мазмұны

Кирхгофтың бірінші заңы

Киргофтың екінші заңы

Кирхгоф заңы арқылы күрделі тізбектегі токты анықтау

Пайдаланған әдебиеттер

Кирхгофтың бірінші заңы

Кез келген түйін тұйықталу нақталатын филиалдарында токтарының алгебралық сомасы нөлге тең болады. Белгілі бір түйін н тұйықталу филиалдары кез келген уақытта токтар I1, I2, . . . , яғни жылы байланысты болса, осы заңға сәйкес

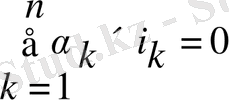
, онда, қазіргі бағыты оң болып табылады және түйіннен бағдарланған (ағымдағы түйінді қалдырады), немесе ағымдағы түйінді кіреді болса. Берілген түйінге қосылған тізбектің филиалдарында токтар қатысты тізбекті тиісті теңдеуінің Осылайша, кез келген түйін.

1-суретте үлгі диаграмма ретінде.

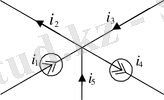
Рис. 1.

Кирхгофа қорытынды бірінші заңға сәйкес

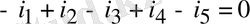
Тораптар тізбегі санына тең тізбегі үшін бірінші Кирхгоф заңы бойынша құрылуы мүмкін теңдеулер жалпы саны.

Осылайша, баған төрт түйіндер үшін (2-сурет) мынадай төрт теңдеулер тұрады болады:

Рис. 2.

узел 1:

\[-\ i_{1}+i_{2}+i_{3}=0\]

узел 2:

\[-\ i_{2}-\ i_{4}+i_{6}=0\]

узел 3:

\[-\ i_{3}+i_{4}+i_{5}=0\]

узел 4:

\[i_{1}\cdot i_{5}\cdot i_{6}=0\]

Бірінші Кирхгоф заңы жиі токтарының үшін Кирхгоф заң аталатын және мәтіндегі қысқартылған отыр KCl көрсетеді.

Осы теңдеулер кез келген тек белгісі басқа үш сомасының әр түрлі болып табылады, өйткені тәуелсіз теңдеулер саны, үш тең. Тізбекті

\[N_{\bar{O}}\]

түйіндерді қамтитын Мәселен, егер, онда ол бірінші заңы Кирхгоф

\[N=N_{\emptyset}-1\]

тәуелсіз теңдеулер жасауға болады. N жиынтығы сызықтық тәуелсіз теңдеулер жүйесі тізбегінде тәуелсіз түйіндердің жиынтығы болып табылады қалыптастыру тұйықталу теңдеулер тораптар.

Кирхгофа қорытынды бірінші заң қолдану мысалдары. Параллель байланыс элементтері

Кирхгоф бірінші заң қолдану мысалы ретінде кедергілер бірнеше элементтерін, конденсаторлар, индуктивтілік катушкалары параллель қосылу қарастыру.

бірнеше элементтерден параллель қосылу ерекшелігі байланысты енгізілген элементтердің кез келген терминалдары қолданылады тең кернеу болып табылады. Осыған байланысты тізбек тек бір тәуелсіз түйіннің сипатталады.

N элементтері параллель қарсылық қосылған делік. Егер сіз осындай 3-суретте көрсетілгендей есеп элементтерін токтарының бағытын таңдасаңыз, элементтердің параллель байланысты Кирхгофа қорытынды бірінші заңға сәйкес, біз жазамыз:

Рис. 3.

\[-\ i+i_{1}+i_{2}+\mathrm{K}\ +i_{n}=0\]

;

есептесек,

\[i_{k}=G_{k}\cdot u\]

, аламыз

\[i_{1}=G_{1}\times u+G_{2}\rtimes u+K+G_{n}u=G\cdot u\]

сонда

\[G=G_{1}+G_{2}+\mathrm{K\Omega}\ G_{n}\]

Тәуелділігі

\[i=G\cdot u\]

терминалы кернеу арасындағы қарым-қатынас түрлі болып табылады және өткізгіштігінің G. бар резистивного элементінде ағымдағы Демек, қатар бірнеше қарсылық тұрады тізбекті өткізгіштік ұялы енгізілген Жүргізіліп элементтерінің сомасы тең, онда, бір белсенді қарсылық ауыстырылуы мүмкін байланысты.

Конденсаторлар параллель (суретте 4) қосылған кезде төмендегідей, ағымдағы филиалы есептеледі:

\[i_{k}=C_{k}\,{\frac{d u}{d t}}\]

Рис. 4.

Филиалдардың токтар қорытындысын қажет жалпы қуаты есептеу үшін:

\[i=C_{1}\frac{d u}{d t}+C_{2}\frac{d u}{d t}+K+C_{n}\frac{d u}{d t}=C\frac{d u}{d t}\]

онда

\[\tilde{N}=\tilde{N}_{1}+\tilde{N}_{2}+\mathrm{K}\ +\tilde{N}_{n}\]

Осылайша, параллель балама сыйымдылығын қосылған кезде бірнеше конденсаторлар байланысты тиесілі сыйымдылықтарды сомасы болып табылады.

Индукторлар (5-сурет) қатарлас байланысты жағдайда, әрбір филиалдың ағымдағы болып табылады:

\[i_{k}=\frac{1}{L_{k}}~\left|{\it\Omega}\times d{\it t}\right.\]

Рис. 5.

Жалпы ток есептеу теңдеуі арқылы беріледі:

\[i=\frac{1}{L_{1}}\otimes\!\!\!\!/u\times\!\!\!/\varepsilon+\frac{1}{L_{2}}\otimes\!\!\!/u\times\!\!\!\!/\varepsilon+...+\frac{1}{L_{n}}\otimes\!\!\!/u\times\!\!\!\!/\varepsilon=\frac{1}{L}~\int\!\!\!/\cdot\!\!\!/u\cdot\!\!\!/\varepsilon\]

Сол себепті

\[{\frac{1}{L}}={\frac{1}{L_{1}}}+{\frac{1}{L_{2}}}+\ldots+{\frac{1}{L_{n}}}\]

, сондықтан

\[{\frac{1}{L}}>{\frac{1}{L_{n}}}\]

Бұл балама индуктивтілік шамасы параллель қосылған индукторлар құндылықтарды ұсақ аз оянады дегенді білдіреді.

Кирхгоф екінші заңы

Кез келген тізбегі тізбегінде филиалдарының кернеулердің алгебралық сомасы нөлге тең болады: мынадай мазмұндағы Кирхгофа қорытынды екінші заңы тұжырымдалған. Тұйық үшін, 6-суретте бейнеленген, біз қатысы жаза аласыз:

\[\textstyle{\frac{n}{2\mu_{k}}}=0\]

Рис. 6.

Қатысты сағат тілімен контурын өту кезінде Кирхгофа қорытынды екінші заңына сәйкес:

\[u_{1}+u_{2}-u_{3}+e_{3}+u_{4}-e_{5}-u_{5}=0\]

Өту бағытын өзгерту қарама-қарсы (минус бірі көбейту) стресс белгілерін өзгерту балама болып табылады.

Кирхгофа қорытынды екінші заң қолдану мысалдары

Жүйелі байланыс элементтері

Дәйекті қосылған п резистивного элементтерін болсын (7 суретті қараңыз) .

Рис. 7.

Екінші Кирхгоф заң тексергіш таңдалған бағытта сәйкес біз теңдеу:

\[u-u_{1}-u_{2}-K-\,u_{n}=0\]

сериясы байланысты ерекшелігі қосылыстар кіретін элементтердің әр токтарының теңдігі болып табылады.

\[u_{k}=i\cdot R_{k}\]

болғанда жазамыз.

\[u=R_{1}\rtimes i+R_{2}\tilde{x}+{\bf K}\;+R_{n}\rtimes i=R\cdot i\]

, яғни

\[R=R_{1}+R_{2}+K\ +R_{n}\]

Осылайша, байланысты енгізілген кедергілер сомасына тең кедергісі балама бірнеше резисторы жалғаған кезде.

Индуктордың жалғаған кезде (8-график) жазуға болады:

\[u-u_{1}-u_{2}-K-\,u_{n}=0\]

Рис. 8.

Егер

\[u_{k}=L_{k}\frac{d i}{d t}\]

, то

\[u=L_{1}{\frac{d i_{1}}{d t}}+L_{2}{\frac{d i_{2}}{d t}}+K+L_{n}{\frac{d i_{n}}{d t}}=L{\frac{d i}{d t}}\]

сондықтан

\[L=L_{1}+L_{2}+K\ +L_{n}\]

Бұл балама индуктивтілік сериясы байланысты енгізілген индуктивті сомасына тең екенін білдіреді.

Екінші Кирхгоф заң үшін конденсаторлар (9-сурет) сериялық байланысты жағдайда жазуға болады:

\[u-u_{1}-u_{2}-K-\,u_{n}=0\]

Рис. 9.

\[u_{k}={\frac{1}{C_{k}}}\ \iint\!d t\]

ауыстыра отырып

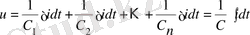аламыз.

Дәйекті қосылған конденсаторлар Кері байланыс сыйымдылығы, қосылыстар кіретін конденсаторлар кері сыйымдылықтарды сомасына тең:

\[{\frac{1}{C}}={\frac{1}{C_{1}}}+{\frac{1}{C_{2}}}+K+{\frac{1}{C_{n}}}\]

Бұл қосылыстар сыйымдылығы сериялық байланысты енгізілген конденсатордың ең төменгі сыйымдылығы аз болады балама болып табылады.

Кирхгоф теңдеулер көмегімен күрделі тізбектерді есептеу

1-мысал

Барлық жағдайларда, тізбегі бірқатар жинау және параллель қосылған филиалдары болып табылады емес. Мысал ретінде, Кирхгоф тізбегінің (сурет 10) теңдеулер көмегімен есептеу мысалын қарастырайық. Тұйықталу

\[N_{\bar{O}}\]

= 4 түйіндерді және

\[N_{\hat{\mathbf{A}}}\]

= 6 кернеу көздері, оның ішінде филиал қамтиды.

Рис. 10.

Тізбегіндегі барлық ағымдағы және кернеу анықтау үшін тізбектің барлық салаларында токтар табуға жеткілікті. Тізбегінің филиалдарының кез келген арқылы өтетін ток біле осы саланың кернеу, және тізбектің түйіндерінің кез келген жұптың арасындағы кернеу ретінде анықтауға болады.

Біз тұйықталу филиалдарында токтарының кез келген оң бағыттарын сұраңыз және өз бетiнше осы токтар нөмірленген болса, онда бірінші Кирхгоф заңы тізбектің филиалдарында токтарының үшін

\[\scriptstyle\aleph_{0}=1\]

теңдеулер болады.

Тізбектің стресс

\[\mathcal{U}_{k}\]

филиалдары үшін

\[N_{\mathrm{B}}-N_{\mathcal{O}}+1\]

сызықтық тәуелсіз теңдеулер үшін Кирхгофа қорытынды екінші заңына сәйкес.

Тәуелсіз теңдеулер - екінші Кирхгоф заң үшін құрастырылған алғашқы Кирхгоф құқық және теңдеулер

\[N_{\mathrm{B}}-N_{\bar{O}}+1\]

, теңдеулер

\[\scriptstyle\aleph_{0}=1\]

жиынтығы,

сызықтық жүйесін қалыптастырады. Оның мүшелері кернеу көздерін орнату үшін тегін болып табылады, өйткені, бұл жүйе, теңдеулер емес бірыңғай жүйесі болады.

Бұл теңдеулер жүйесі сіз тізбектің кез келген екі тораптары арасындағы тізбектің филиалдарында, сондай-ақ олардың токтар кернеулердің мәндері табуға мүмкіндік беретін бірегей шешімі бар.

Мысалы, (10-график) бірінші Кирхгоф заң теңдеулер жүйесін орнату. Теңдеулер саны:

\[N_{\mathrm{GD}}=N_{\mathrm{O}}-1=4-\,1=3\]

Узел 1:

\[-\ i_{1}+i_{2}+i_{3}=0\]

узел 2:

\[-\ i_{2}\,\mathrm{,}\mathrm{,}\ i_{4}+i_{6}=0\]

узел 3:

\[-\ i_{3}+i_{4}+i_{5}=0\]

Сонымен қатар Контур үшін Крихгофтың екінші заңы I, II, III

\[N_{\mathrm{GD}}\]

- дан теңдеулер жүйесінен құруға болады.

\[N_{\mathrm{GB}}=N_{\mathrm{B}}-\,N_{\bar{O}}+1=3\]

Контур I:

\[\mathbf{\nabla}-U+R_{0}\rtimes\dot{x}_{2}+R_{2}\rtimes\acute{x}_{6}=0\]

контур II:

\[\quad-\ R_{0}\rtimes\alpha_{2}+R_{1}\ ;\alpha_{3}+R_{0}\cdot\chi_{4}=0\]

контур III:

\[\check{\ }\ \ \ \ \ \ -\ R_{0}\ \check{\bf x}_{4}+R_{0}\ \check{\bf x}_{5}\ -\ R_{2}\ \check{\bf x}_{6}=0\]

Осылайша, Крамер анықтау белгісіз әдісімен мысалы алты белгісіз ағымдардың, 6 теңдеулер жүйесін шешу. Тұйықталу ағымдағы көзі болса, теңдеулер жүйесі осы көзден соңын белгісіз кернеу, және көзі ток арқылы ағымдағы мастер көзіне тең. Белгісіз жалпы саны өзгеріссіз қалады.

Үлгі 2

Тізбек үшін ( 11 сурет ) токтарды анықтау

\[\left.{\frac{\mathrm{o}}{{\hat{\ell}}}{\cos}}\right|\]

\[i_{\mathrm{2}}\]

, егер E = 20 В, I ₀ = 2 A, R ₁ = 15 Ом, R ₂ = 85 Ом.

Рис. 11.

Шешімі:

Кирхгоф заң теңдеулер дейін

\[\left.{\frac{\mathrm{e}}{{\hat{\ell}}}{\cos}}\right|\]

\[i_{\mathrm{2}}\]

және айналма тізбегі токтарының, бағытын таңдаңыз. Теңдеулер саны бірінші Кирхгоф заң болып табылады:

\[N_{\mathrm{OB}}=N_{O}\ -1=2-\ 1=1\]

Кирхгофтың екінші заңы бойынша теңестіру саны:

\[N_{\Theta B}=N_{\bf B}\,-\,N_{O}\,+1-\,N_{\bf\hat{E}\hat{O}}=3\,-\,2+1\,-\,1=1\]

Ағымдағы 1 түйін үшін теңестіру :

\[\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O O\]

. (a)

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.