Модуль (абсолют шама): анықтама, қасиеттері және модульмен берілген теңдеулерді шешу әдістері


Кіріспе
Тұрмыста кейбір шамалардың (ұзындықтың, массаның, температураның) өзгерістерінің сан мәні ғана жазылады. Өзен суы деңгейінің өзгерісі 20см. Мұнда өзен суының деңгейі 20см-ге жоғары көтерілді ме немесе 20 см-ге төмен түсті ме, оған назар аударылмайды. Демек берілген санның оң не теріс сан екені ескерілмейді. Тек өзен суының соңғы деңгейінің алғашқы деңгейінен айырмашылығы 20см, мұны математикада санның модулі деп атайды.
Жазылуы:20=20, -20=20
Оқылуы:20 немесе -20 санының модулі 20-ға тең.
Модуль - латынның modulus деген сөзі-«мөлшер»дегенді білдіреді. Кейбір жағдайда «модульдің» орнына абсолюттік шама деп те атайды. Модуль белгісін 1841 жылы неміс математигі Карл Вейерштрасс (1815-1897) енгізген. Бұл көп мағыналы сөз, математикамен қатар ол архитектурада, физикада, техникада, тағы басқа ғылымдар программасында кездеседі.
Архитектурада -бұл өлшем бірлігі, архитектура құрылыстары үшін орнатылады және оның элементтер құрамының сәйкестігі үшін пайдаланылады.
Техникада -бұл термин, техниканың әрбір аймағында қолданылады, универсаль емес мән мен әртүрлі коэфициенттер және ұзындықтарын белгілеу үшін қолданылады.
Физикада -көлем қысымдылық модулі-материал ішінде нормаль күштің ұзындығына қатынастығы үшін қолданылады.
I. Модуль және оның қасиеттері
1. 1. Түсінік және анықтама
Бұл тақырыпты кеңірек оқып үйрену үшін, маған қажет болатын қарапайым анықтамалар туралы түсінік келтіруді жөн санадым.
Теңдеу - бұл айнымалысы бар теңдік.
Модуль таңбасы бар теңдеу - айнымалысы модуль таңбасы немесе абсолют шама астында болатын теңдеу. Мысалы: x=1
Теңдеуді шешу- бұл барлық түбірді табу немесе түбірі жоқ екенін дәлелдеу.
Математикада модульдің әртүрлі мағынасы бар, мен өзімнің зерттеу жұмысымда тек бір мағынасын қарастырдым.
Модуль -санның абсолют шамасы, сандық түзуде санақ басынан берілген санға сәйкес нүктеге дейінгі қашықтық.
1. 2. Теореманың дәлелдемесі
Анықтама : а санының модулі немесе а санының абсолют шамасы а -ға тең, егер а нольден үлкен немесе тең болса, -а -ға тең, егер а саны нольден кіші болса, яғни
a, егер а≥0
a=
-а, егер а<0
Анықтамадан кез келген нақты а саны үшін a≥0 екендігі шығады.
Теорема 1 . Кез келген а≠0 нақты санының абсолют шамасы а және -а сандарының үлкеніне тең болады.
Дәлелденуі
1. Егер а оң сан болса, онда -а теріс сан, яғни -а<0<a, бұдан -a<a.
Мысалы: 5 оң сан, -5 теріс сан және -5<0<5, бұдан -5<5.
Бұл жағдайда a=a, яғни a мәні а және -а сандарының үлкеніне тең болады.
2. Егер а теріс сан болса, онда -а оң сан болады және а<-а, яғни үлкен сан -а. Анықтама бойынша a=-a, бұл жағдайда да -а және а сандарының үлкені -а-ға тең болатыны шығады.
Салдар1. Теорема бойынша -a=a. Бұл жағдайда -a және a шамасы -а және а сандарының үлкеніне тең болады.
1 Т. А. Алдамұратова «Математика-6» Алматы «Атамұра»2006 ИБ №064 82, 84 бет.
Салдар2. Кез келген нақты а саны үшін а ≤ a, -a ≤ a теңсіздіктері тура болады.
Екінші теңсіздікті (-а ≤ a ) -1-ге көбейтсек (бұл жағдайда теңсіздік таңбасы қарама-қарсы таңбаға өзгереді) а ≥-a теңсіздігі кез келген нақты а саны үшін тура болады. а≤a және а≥-a теңсіздіктерін біріктіріп
-a ≤ a ≤ a қос теңсіздігін аламыз.
Теорема2.
Кез келген нақты а санының абсолют шамасы а
2
санының арифметикалық квадрат түбіріне тең болады, яғни a=
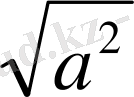 ;
;
Бұл жағдайда а≥0 болса, анықтама бойынша a=a, екінші жағынан а≥0,
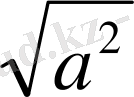 =a, яғни a=
=a, яғни a=
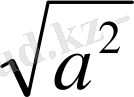
Егер а<0, онда a=-a және
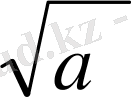 =-a бұл жағдайда a=
=-a бұл жағдайда a=
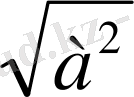
Бұл теореманы пайдаланып a ны
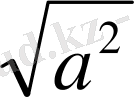 пен алмастыру арқылы кейбір теңдеулерді шешуге болады. Геометриялық мағынасы бойынша a координаталық түзудің бас нүктесінен a-ға сәйкес нүктеге дейінгі қашықтық. Егер а≠0 болса, онда координаталық түзуде а және -а сандарына сәйкес О нүктесінен бірдей қашықтықта екі нүкте болады, яғни a=-a. Егер а=0 болса, онда a координаталық түзуде О нүктесімен кескінделеді (1-сурет) .
пен алмастыру арқылы кейбір теңдеулерді шешуге болады. Геометриялық мағынасы бойынша a координаталық түзудің бас нүктесінен a-ға сәйкес нүктеге дейінгі қашықтық. Егер а≠0 болса, онда координаталық түзуде а және -а сандарына сәйкес О нүктесінен бірдей қашықтықта екі нүкте болады, яғни a=-a. Егер а=0 болса, онда a координаталық түзуде О нүктесімен кескінделеді (1-сурет) .
a a
1-сурет
-а 0 а
II. Модуль таңбасымен берілген теңдеулерді шешу әдістері
Модуль таңбасымен берілген теңдеуді шешу үшін, біз санның модулінің анықтамасын және абсолют шама қасиеттерін негізге аламыз. Біз бірнеше мысалды әртүрлі тәсілмен шешуді қарастырып, олардың қайсысы тиімді екендігін көреміз.
Модуль белгісінің астында айнымалы шама болатын теңдеулерді шешудің мектеп программасындағы белгілі әдістері:
1. Модульдің геометриялық мағынасын пайдалану
2. Графиктік әдіс
3. Анықтама бойынша модульді ашу
Модуль таңбасымен берілген теңдеуді шешуде модульдің геометриялық мағынасын пайдалану.
x-a модулінің геометриялық мағынасы-координаталық түзуде х және а нүктелерінің арақашықтығы.
Мысал: x-1+x-2=1 модульдің геометриялық мағынасын пайдаланып теңдеуді шешейік. Ол үшін мына түрде талдау жасауға болады. Теңдеудің сол жақ бөлігінде х нүктесінен қашықтығы 1-ге және 2-ге тең болатын нүктелердің абсциссаларының қосындысын табамыз, яғни [1; 2] кесіндісіндегі барлық нүктелер берілген теңдеудің түбірі бола алады, ал ол кесіндіден тыс нүктелер абсциссалары теңдеу шешімі бола алмайды. Бұл жағдайда теңдеу шешімі [1; 2] кесіндісі болады.
Жауабы: x
 [1; 2]
[1; 2]
Мысал: x-1-x-2=1 теңдеуін шешейік.
Бұл теңдеудің сол жағындағы өрнек бойынша х нүктесінен қашықтығы 1 және 2 болатын нүктелердің абсциссаларының айырмасы 1-ге тең болатын аралық координаталық осьте 2 санының оң жағы, яғни берілген теңдеу шешімі бұл жағдайда кесінді емес, басы 2 санына тең нүкте болатын ох осінің оң бағытындағы сәуле болады.
Жауабы: x
 [2; ∞)
[2; ∞)
Бұл мысалдардан мынадай қорытынды жасадым.
x-a + x-b=b-a, егер b≥a
 a≤x≤b
a≤x≤b
x-a - x-b=b-a, егер b≥a
 x
x
Графиктік әдіс
Модуль таңбасымен берілген теңдеулерді шешудің бір әдісі -графиктік әдіс. Бұл әдіс функция графигін тұрғызуға негізделген. Егер берілген функциялар графиктері қиылысса, онда қиылысу нүктелерінің абсциссалары берілген теңдеу шешімі болады. Егер графиктер қиылыспаса, онда берілген теңдеу шешімі болмайды деген қорытындыға келеміз. Бұл әдіс модуль таңбасымен берілген теңдеулерді шешудің басқа әдістеріне қарағанда онша тиімді емес, себебі біріншіден, ол уақытты көп алады және үнемі рационалды емес, екіншіден график тұрғызғандағы нәтиже үнемі дәл болмайды.
Анықтама бойынша модульді ашу
Модуль таңбасымен берілген теңдеуді шешудің тағы бір әдісі-модуль анықтамасы бойынша модульді ашу, яғни кез келген f(х) функциясы үшін
f(х), егер f(х) ≥0 болса
f(х) =
-f(х), егер f(х) <0, болса
1-мысал . Теңдеуді шешу керек: 2x-5=1
Шешуі:1-ші тәсіл. a-b модулінің геометриялық мағынасы-түзудегі а мен b нүктелерінің арақашықтығы екенін ескерсек, жалпы жағдайда x-a=r түріндегі теңдеуді шешу үшін түзудегі а нүктеден r қашықтықта орналасқан екі нүктені тапса болғаны.
Біздің мысалымызда түзу бойында 5 санына сәйкес нүктеден 2х-ке сәйкес нүктеге дейінгі қашықтық 1-ге тең болатын екі нүкте бар, олар: 6; 4. Олай болса 2х=6 және 2х=4 теңдеулерін аламыз, бұдан х=3 және х=2. Жауабы:3 және 2.
4 5 6 f(х), f(х) ≥0
2-тәсіл. Анықтама бойынша f(х) =
-f(х), f(х) ≤0 болатындықтан
модульді ашамыз, егер өрнек теріс емес болса, онда модульден оң мәнмен шығады, яғни 2х-5=1. Егер модуль астындағы өрнек теріс болса, онда -(2х-5) =1 немесе 2х-5=-1 болады.
2х-5≥0 x≥2. 5
2x-5=1 2х-5=1 x=3
2х-5≤0 x≤2. 5
-(2х-5) =1 x=2 2 2, 5 3
Жауабы:2және 3.
Егер модуль таңбасымен берілген өрнек оң а санына тең болып берілсе, онда модуль астындағы өрнек а немесе -а санына тең болады деген қорытынды жасадым.
3-әдіс. y=2x-5, y=1 функцияларының графигін сызамыз. y=2x-5 функциясында x=2, 5 болғанда y=0, яғни ох осімен (2, 5; 0) нүктесінде, ал оу осімен (0; 5) нүктесінде қиылысатын түзу, у=1 графигі ох осіне параллель (0; 1) нүктесінен өтетін түзу. Олар А(2; 0), В(3; 0) нүктелерінде қиылысады, яғни жауабы x=2, x=3.
2-мысал. 1+x=0. 5 теңдеуін шешу керек.
1-әдіс. Теңдеуді түрлендірсек x=0. 5-1 мәндес теңдеу шығады, бұдан x=-0. 5 болады, модуль анықтамасы бойынша x≥0 яғни x≠-0. 5 олай болса теңдеу шешімі жоқ.
Жауабы: құр жиын.
2-әдіс. х≥0 х≥0 -0, 5
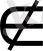 [0; ∞)
[0; ∞)
1+х=0. 5 x=-0. 5
x<0 x<0
1-x=-0. 5 x=1. 5 1. 5
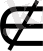 (-∞; 0)
(-∞; 0)
Яғни берілген теңдеудің шешімі жоқ.
Жауабы: құр жиын.
3-әдіс. 1+x=0. 5
 x=-0. 5
x=-0. 5
y=x және y=-0. 5 графиктерін саламыз, олар қиылыспайды, олай болса берілген теңдеудің шешімі жоқ.
Жауабы: құр жиын.
3-мысал. x 2 +3x=2(х+1) теңдеуін шеш.
Шешуі: Бұл теңдеуге мәндес жүйе аламыз, яғни
x 2 +3x=±2(х+1) x 2 +x-2=0 x 1 =-2, x 2 =1 x=1
 x
2
+5x+2=0
x
2
+5x+2=0
 x
3, 4
=
x
3, 4
=
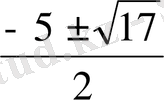 Equation. 3
Equation. 3
 Equation. 3 x=
Equation. 3 x=
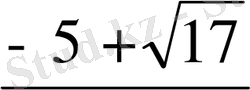
х+1≥0 x≥-1 x≥-1 x=
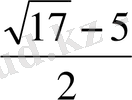 Equation. 3
Equation. 3
Жауабы:
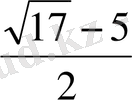 Equation. 3 ; 1
Equation. 3 ; 1
4-мысал . x 2 -4х+x-3+3=0 теңдеуін шеш.
Координаталық ості екі бөлікке бөліп, сол бөліктерге сәйкес теңдеу шешімін табамыз.
x<3 x≥3
x-3= -x+3 x-3=x-3
x 2 -4x-x+3+3=0 x 2 -4x+x-3+3=0
x 2 -5x+6=0 x 2 -3x=0
x 1 =2, x 2 =3 x=0, x=3
x=3-бөгде түбір, ол x=0-бөгде түбір, ол
(-∞; 3) аралығына тиісті емес. [3; ∞) сәулесіне тиісті емес.
Яғни берілген теңдеудің екі шешімі бар, олар x 1 =2, x 2 =3.
Жауабы: x 1 =2, x 2 =3.
5-мысал. Теңдеуді шеш: 2x+8-x-5=12
Шешуі: Екі модульді де ашқанда үш жағдайға келеміз. (х+4≤0, х-5≥0 ескермегенде)
2x+4-x-5=12
 x+4≤0 x≤-4
x+4≤0 x≤-4
x-5≤0 x= -25 x=-25
-2x-8+x-5=12 x=-25
x+4>0 -4<x<5 x=3 x=3
x-5≤0 x=3
2x+8+x-5=12 x
 ø
ø
x+4>0 x>5
x-5>0 x=-1
2x+8-x+5=12
Жауабы:{-25; 3}.
6-мысал : теңдеуді шеш 3x+2+x 2 +6x+2=0
Шешуі: Екі жағдайды қарастырамыз.
1) х+2≥0 х≥-2

 х=-1
х=-1
x 2 +9x+8=0 x=-1, x=-8
2) х+2<0 x<-2
 Equation. 3
Equation. 3
 Equation. 3 x=-4
Equation. 3 x=-4
x 2 +3x-4=0 x=-4, x=1
Жауабы: (-4; -1)
7-мысал : теңдеуді шеш 4-x+ (х-1) (х-3) =1
Шешуі:1-әдіс. 4-x=x-4 теңдігін пайдаланып, төрт жағдайды қарастырдым.
1) x - 4 ≥ 0 x ≥ 4 x ≥ 4


 x
x
 ø,
ø,
x-4+x
2
-4x+3=1 x
2
-3x-2=0 x=
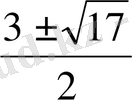
яғни
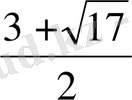 <4.
<4.
2) 3 < x < 4 3 < x < 4 3 < x < 4


 x
x
 ø.
ø.
4-x+x 2 -4x+3=1 x 2 -5x+6=0 x=3; x=2
3) 1 ≤ х ≤ 3 1 ≤ х ≤ 3 1 ≤ х ≤ 3


 х=3
х=3
4-x-x 2 +4x-3=1 x 2 -3x=0 x=0; x=3
4) x<1 x<1 x<1
 Equation. 3
Equation. 3
 Equation. 3
Equation. 3
 Equation. 3 x
Equation. 3 x
 Equation. 3 ø
Equation. 3 ø
4-x+x 2 -4x+3=1 x 2 -5x+6=0 x=2; x=3
Жауабы: x=3.
2-әдіс.
y= (х-1) (х-3) , y=1-x-4 функцияларының графигін сызамыз.
1) y= (х-1) (х-3) функциясында х 1 =1 және х 2 =3 болғанда, сәйкес у 1 =0,
y 2 =0 болады, яғни ох осімен (1; 0), (3; 0) нүктелерінде қиылысады. Ал х=0 болғанда y=3, яғни оу осімен (3; 0) нүктесінде қиылысады.
х
0
=
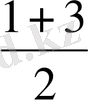 =2, y
0
= (2-1) (2-3) =1, яғни (2; 1) нүктесі берілген функцияға сәйкес парабола төбесі, х=2 түзуі симметрия осі болады, яғни берілген функция графигі осы түзуге қарағанда симметриялы болады. Графиктің ох осінен төмен жатқан бөлігінің ох осіне қарағанда айналық бейнесін салсақ
=2, y
0
= (2-1) (2-3) =1, яғни (2; 1) нүктесі берілген функцияға сәйкес парабола төбесі, х=2 түзуі симметрия осі болады, яғни берілген функция графигі осы түзуге қарағанда симметриялы болады. Графиктің ох осінен төмен жатқан бөлігінің ох осіне қарағанда айналық бейнесін салсақ
у= (х-1) (х-3) функциясының графигін саламыз.
2) у=1-x-4 функциясының графигін салу үшін оның ох осімен қиылысу нүктесінің абсциссасын табамыз, ол үшін 1-x-4=0 қарапайым теңдеуін шешеміз. x-4=1, x-4=1 немесе x-4= -1
x=5 x=3
Яғни бұл график ох осімен (5; 0), (3; 0) нүктелерінде қиылысады. х=4 болғанда y=1. Сонда берілген екі функцияның графигі x=3 нүктесінде ғана қиылысады.
Жауабы:3.
2 Е. Ж. Айдос «Математика-жоғары оқу орнына түсушілерге арналған» Алматы-2006 ЖШС РПБК «Дәуір» 180, 184, 186 бет.
2. 1. а және b сандарының модульдері мен квадраттарының арасындағы байланыс арқылы шешу.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz