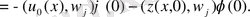Жүктелген параболалық теңдеулерде коэффициент арқылы тиімді басқару: шешімнің бар болуы, жеткілікті шарттар және итерациялық алгоритмдер


Дипломдық жұмыс
Тақырыбы: ЖҮКТЕЛГЕН ПАРАБОЛАЛЫҚ ТЕҢДЕУДІ КОЭФФИЦИЕНТ АРҚЫЛЫ БАСҚАРУ.
Мазмұны
КІРІСПЕ . . . 4
1. ЖОРАМАЛ БАҒАЛАР ЖӘНЕ ШЕШІМНІҢ БАР БОЛУЫ ЖӘНЕ ЖАЛҒЫЗДЫҚ ТЕОРЕМАСЫ . . . 7
1. 1. Есептің қойылуы . . . 7
1. 2. Шектік есептің бар болуы және жалғыздық теоремасы . . . 8
2. ТИІМДІЛІКТІҢ ЖЕТКІЛІКТІ ШАРТЫ . . . 18
2. 1. Тиімді шешімнің бар болуы . . . 18
2. 2. Тиімділіктің жеткілікті шарты . . . 19
2. 3. Итерациалық алгоритм . . . 22
2. 4 Модельдік есеп үшін итерациялық алгоритм. 24
ҚОРЫТЫНДЫ . . . 30
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР . . . 31
Кіріспе
Қазіргі кезде тиімді басқару теориясында дербес туындылы теңдеулерімен сипатталатын есептер ерекше орын алады. Көптеген әдебиеттерде жүйелердің шешімділігі, жеткілікті шарты көрсетілген және шешу алгоритмі құрастырылған. Тиімді басқару теориясына бағытталған ғылыми жұмыстардың арасында келесі А. Г Буковскийдің /1/ Ж. Л. Лионстың /2/ еңбектерін айтуға болады дербес туынды теңдеулермен сипатталатын тиімді басқару есептерінде басқару көп жағдайларда оң жағынан немесе шекаралық және бастапқы шарттарына кіреді. Коэффицент арқылы басқару жүйелері сызықты емес және жеке зерттеуді қажет етеді. Коэффицент арқылы басқару системасы С. Я. Серовайскийдің /3/, Ж. Л. Лионстың /2/ еңбектерінен қарастырылған. Тиімді басқару теориясын оқи отырып көптеген проблемалдардың ішіндегі дербес туындылы есеп үшін шектік есебіне қатысты жүктелген теңдеулер ерекше орын алады. Жүктелген теңдеуі мынандай
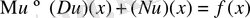 обылысында
обылысында
 (1)
(1)
мұндағы
 - дифференциалды оператор
- дифференциалды оператор

 - дифференциалды және интегро-
- дифференциалды және интегро-
 - дифференциалды оператор.
- дифференциалды оператор.
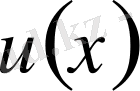 функциясы бойынша
функциясы бойынша
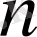 - нен кіші өлшемді
- нен кіші өлшемді
 көп бейнелеуде ізін алу операциясын құрайды.
көп бейнелеуде ізін алу операциясын құрайды.
1-түрдегі теңдеулер математикалық физиканың теріс есептерінде сызықты емес теңдеулерін зерттегенде интегро дифференциялдық теңдеулердің сандық шешімін алғанда, динамикалық объектілерді (мұнай және газ сымдарында) басқаруда т. с. с жүйелерде кездеседі. жүктелген теңдеулер шекаралық есептер үшін кең тараған теорияны тік қолдануға мүмкіндік жоқ.
Жүктелген интегралдық теңдеуін В. М. Будака, А. Д. Искендировтың (/4, 5/) еңбектерінде зерттелген.
А. М. Нахушевтың және оның шәкіртерінің еңбектерінде жүктелген теңдеуі үшін шектік есебі тереңдете айтылған. Оның жұмысында және оның шәкірттерінің жұмысында үзіліссіз функциялар класында жүктелген теңдеулердің шешімінің бар және жалғыз болуы қарастырылған. Осы бөлімде параболалық типте жүктелген теңдеуі үшін шектік есептің Соболев кеңістігіндегі шешілу А. Д. Искендировтың, Будаканың (/4, 5/) М. Т. Дженалиевтың жұмыстарынан оқығамыз.
Уақытқа байланысты физикалық жүйені қарастырайық
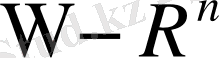 шектеуі Г болатын кеңістіктегі облыс (жиын)
шектеуі Г болатын кеңістіктегі облыс (жиын)
Бұл аймақтық Г-шегіндегі біржақты локальды
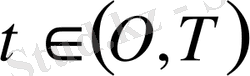 үзілісті деп,
үзілісті деп,
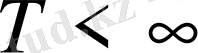 ,
,
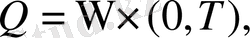
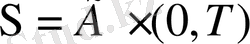 ,
,
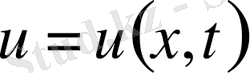 -есептің шешімі
-есептің шешімі
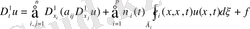
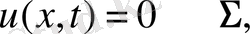 обылысында
обылысында
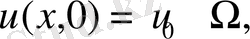 обылысында (2)
обылысында (2)
мұндағы
 - басқару
- басқару
 - дөңес тұйық жиын
- дөңес тұйық жиын
 .,
.,
 өлшемді көпбейнелер Ω
өлшемді көпбейнелер Ω
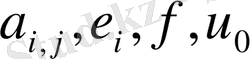 есептің қойылуы
есептің қойылуы
- функционалды минимумға жеткізетінжұпты таңдап аламыз
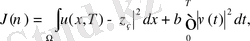 (3)
(3)
мұнда
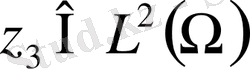 ,
,
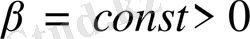 ,
,
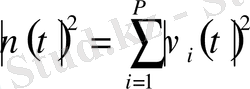 ,
,
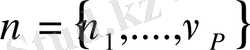 ,
,
Коэффициенті регулярлы емес шектік есептің шешілуі және сызықты жүктелген параболалық типтің теңдеуі үшін тиімді басқару сұрақтары, басқару коэффициентін зерттеу жұмыстары қарастырылды . Бірақ жүктелген теңдеу басқару коэффициенті қосымды жүктелген жағдайда кейбір әртүрлі
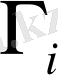 мөлшерінде бірінші рет қарастырылады Сондықтан есептің қойылымы жай болып табылады ал бұдан актуалдық проблема
мөлшерінде бірінші рет қарастырылады Сондықтан есептің қойылымы жай болып табылады ал бұдан актуалдық проблема
Бітіру жұмыстың мақсаты шектік есептің шешімділігін, жүктелген параболалық теңдеудің коэффициентерін тиімді басқару есебінің шешімінің бар болуын зерттеу, тиімділіктің жеткілікті шартын алу, итерациялық алгоритм құрастыру.
1. Жорамал бағалар және шешімінің бар болу және
жалғыздық теоремасы.
1. 1 Есептің койылуы.
Басқару есебі келесі түрдегі шектік есеп арқылы берілсін.
 - шектелген Т шекаралы облыс болсын:,
- шектелген Т шекаралы облыс болсын:,
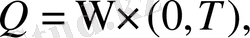
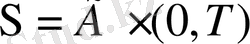 ,
,
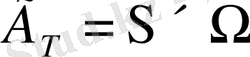 ,
,
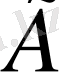
 облысының бір жағында локальды жатады. Келесі шектік есеппен бейнеленген басқару процесін қарастырайық. .
облысының бір жағында локальды жатады. Келесі шектік есеппен бейнеленген басқару процесін қарастырайық. .
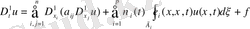
 , (4)
, (4)
облысында
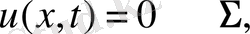 обылысында (5)
обылысында (5)
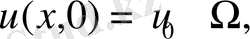 обылысында (6)
обылысында (6)
Мұндағы
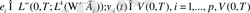 - дөңес, тұйық жиын
- дөңес, тұйық жиын
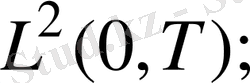
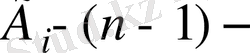 өлшемді көпбейнелер
өлшемді көпбейнелер
 -да,
-да,
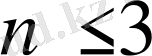 бекітілген нүктелер
бекітілген нүктелер
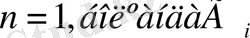
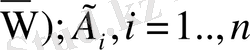 мен
мен
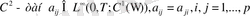 үшін
үшін
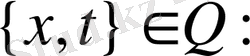
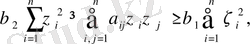 (7)
(7)
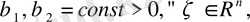
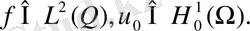
Сапалық критерийі келесі функционалмен берілген
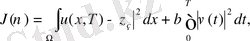 (8) мұнда
(8) мұнда
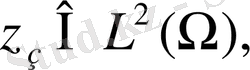
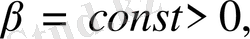
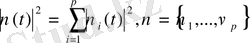 .
.
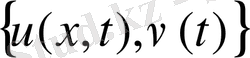 Тиімді басқару есебі (4) -(7) шарттарды қанағаттандыратын және (8) функционалды минимумға жеткізетін жұпты табу керек. Бізге белгілі, ортақ сұрақтың біреуі, шекаралық есеп теориясында дербес туындылы теңдеу үшін функционалдық кеңістіктерді таңдау. Осы бөлімде параболаның типте жүктелген теңдеуі үшін шектік есептің Соболев кеңістігіндегі шешілу қарастырылады. (4) -(6) шектік есептің бір мәнді шешілу теоремасы және тура таңдалған кеңістіктің функционалы орнатылған.
Тиімді басқару есебі (4) -(7) шарттарды қанағаттандыратын және (8) функционалды минимумға жеткізетін жұпты табу керек. Бізге белгілі, ортақ сұрақтың біреуі, шекаралық есеп теориясында дербес туындылы теңдеу үшін функционалдық кеңістіктерді таңдау. Осы бөлімде параболаның типте жүктелген теңдеуі үшін шектік есептің Соболев кеңістігіндегі шешілу қарастырылады. (4) -(6) шектік есептің бір мәнді шешілу теоремасы және тура таңдалған кеңістіктің функционалы орнатылған.
1. 2. Шектік есептің бар болу және жалғыздық
теоремасы.
Теорема 1
. (7) шарт орындалсын онда
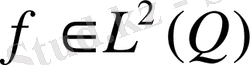 және
және

(4) -(6) есептің
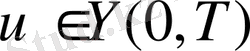 .
жалғыз шешімі болады. Бұл шешім бастапқы берілгендерден үзіліссіз тәуелді, яғни
.
жалғыз шешімі болады. Бұл шешім бастапқы берілгендерден үзіліссіз тәуелді, яғни
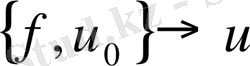 бейнелеу
бейнелеу
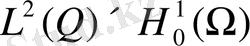 кеңістігінен
кеңістігінен
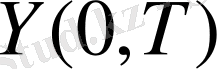 кеңістігіне үзіліссіз бейнелеу.
кеңістігіне үзіліссіз бейнелеу.
Мұндағы.,
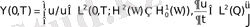 .
.
Д/уі:
(4) теңдеуінен
 ға скаляр көбейтейік.
ға скаляр көбейтейік.
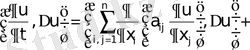 (9)
(9)
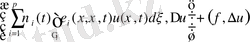 ,
,
мұндағы
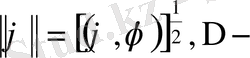 Лаплас операторы
Лаплас операторы
Содан, келесі теңсіздікті пайдаланайық:
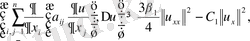 (10)
(10)
үшін
 және
және
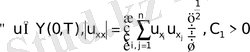 .
.
(9) -теңсіздіктен, (10) теңсіздікті пайдаланып аламыз
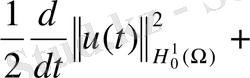
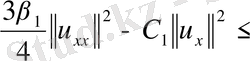
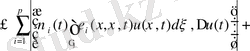
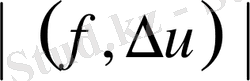 . (11)
. (11)
Бірінші қосындыны (11) теңсіздіктің оң жағын Гальдер (4) теңсіздігі арқылы бағалайық.
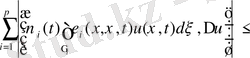
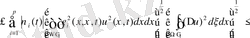
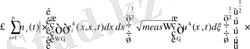
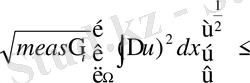 (12)
(12)

мұнда
 теңсіздіктен
теңсіздіктен
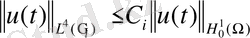 ,
,
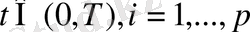 (13)
(13)
Онда (11) -ден аламыз
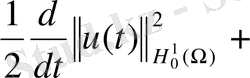
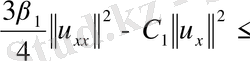
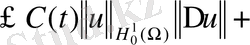
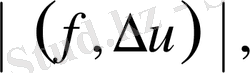
мұнда
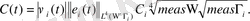
Содан соң,
 Коши теңсіздігін пайдаланып
Коши теңсіздігін пайдаланып
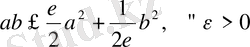 , (14)
, (14)
келесі түрде жазуға болады
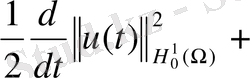
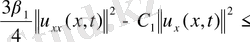
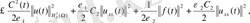
мұнда

. теңсіздіктен алынды
-ны
шартынан таңдап алатынымыз:
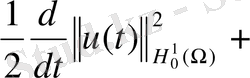
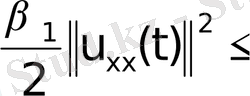
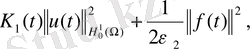 (15)
(15)
Мұнда
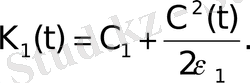
теңсіздіктен алуға болады
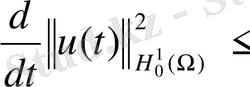
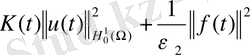 , (16)
, (16)
Мұнда
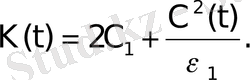
Кейін, Гронуолл лемманың дәлелін пайдаланамыз(16) - ның екі жағын
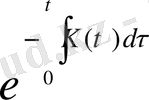 - ға көбейтеміз бірінші бөлігін оң жағын сол жаққа тасымалдап, және нәтижесін теңсіздік түрінде жазамыз.
- ға көбейтеміз бірінші бөлігін оң жағын сол жаққа тасымалдап, және нәтижесін теңсіздік түрінде жазамыз.
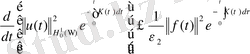 Equation. 3 .
Equation. 3 .
Оны 0-ден t-бойынша интегралдап және
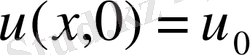 , ескеріп аламыз:
, ескеріп аламыз:
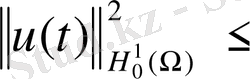
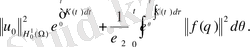
Осыдан шығатыны:
 (17)
(17)
(17) мен (15) -теңсіздіктің оң жағына стандарттық жолмен қоямыз.
 (18)
(18)
(17) (18) (4) теңдеуін бағалау негізінде және
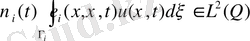 ескеріп келесі баға аламыз.
ескеріп келесі баға аламыз.
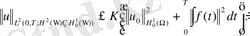 (19)
(19)
Зерттеуді әрі қарай жалғастыру үшін Галеркин әдісін қолданамыз
 , болатын базис кеңістігі
, болатын базис кеңістігі
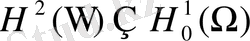 , яғни кез келген
, яғни кез келген
 элементінің
элементінің
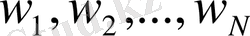 сызықты тәуелсіз
сызықты тәуелсіз
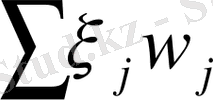 сызықты комбинациясы
сызықты комбинациясы
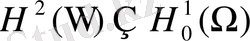 тығыз
тығыз
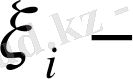 сандар (6) есептің шешімін келесі түрде анықтайық.
сандар (6) есептің шешімін келесі түрде анықтайық.
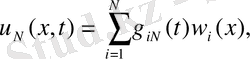 (20)
(20)
мұнда
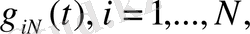 функциялары келесі шартын қанағаттандыратындай етіп алынады.
функциялары келесі шартын қанағаттандыратындай етіп алынады.
 ,
,
(21)

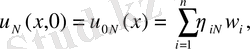 . 3 мұнда
. 3 мұнда
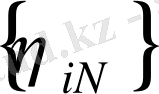
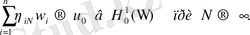 . 3 (22)
. 3 (22)
(21) -(22) Коши есебі сияқты болады, олар сызықты дифференциалдық теңдеу жүйесі үшін
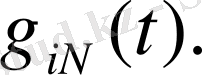 функциясына сәйкес
функциясына сәйкес
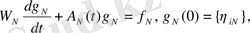
мұнда
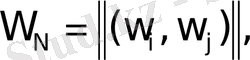
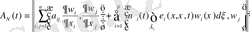 ,
,
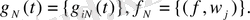
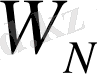 - Грамма матрица болғандықтан және
- Грамма матрица болғандықтан және
 арқылы
арқылы
(21) -(22) есебі бір ғана абсолютті үзіліссіз шешімі болады.
Көрсетейік, егеp
 онда
онда
 , және
, және
 -есептің шешімі болады
-есептің шешімі болады
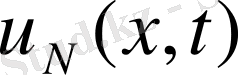 теңдеудің шешімі әрбір N кезінде жорамал бағасы 15 түрінде орын алады, онда шектелген тізбектен
теңдеудің шешімі әрбір N кезінде жорамал бағасы 15 түрінде орын алады, онда шектелген тізбектен
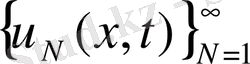 тізбекше бөліп алуғаболады
тізбекше бөліп алуғаболады
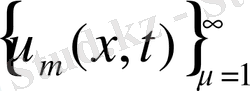 ,
,

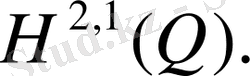 (23)
(23)
Теорема немесе лемма бойынша, сызықты үзіліссіз бейнелеу тізбектелген жинақтау аркылы аламыз.

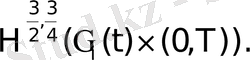 (24)
(24)
24-тен шығатыны

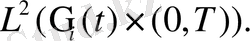 (25)
(25)
j- еркін бекітілген сан немесе
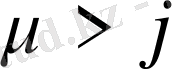 . болсын. Өйткені (16) -да
. болсын. Өйткені (16) -да
 , тең болады . Оны функцияға көбейткенде.
, тең болады . Оны функцияға көбейткенде.
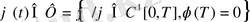
және 0-ден Т бойынша интегралдап:
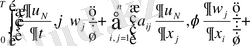 (26)
(26)
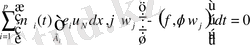 .
.
Жеке - жеке интегралдаймыз
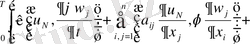
онда бөліктеп интегралдау арқылы, аламыз.
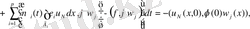
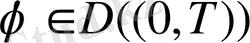 , - ді ақырсыз сан, бір ғана рет дифференциалданатын және финиттық функция болатын ретінде алайық, онда шекке көшіп
, - ді ақырсыз сан, бір ғана рет дифференциалданатын және финиттық функция болатын ретінде алайық, онда шекке көшіп
 табамыз (23) - (24) .
табамыз (23) - (24) .
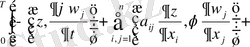 Equation. 3 (26)
Equation. 3 (26)
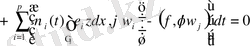
Кез келген j және кез келген
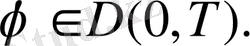
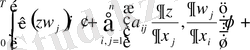
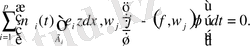
(27)
Шварц туынды анықтамасы бойынша
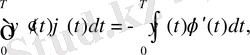 бұдан кейін аламыз.
бұдан кейін аламыз.
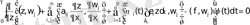 ,
,
кез келген j және кез келген
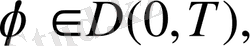 мұнда
мұнда
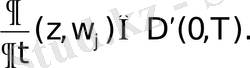
Анализден белгілі
 яғни
яғни
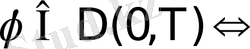
 ,
,
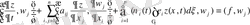 . (28)
. (28)
Содан кейін j-еркін, ал сызықты комбинация жиыны
 . 3 элементі тығыз
. 3 элементі тығыз
 , болады: Онда (25) шығады.
, болады: Онда (25) шығады.
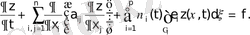 (29)
(29)
Бұдан
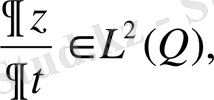 яғни
яғни
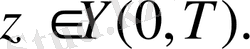 Қорыту үшін тек қана тексеру қалды Z
Қорыту үшін тек қана тексеру қалды Z
бастапқы шартын қанағаттандыратын
 функциясын алайық Онда
функциясын алайық Онда
 аламыз:
аламыз:
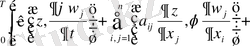 (30)
(30)
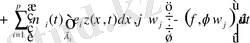 =
=
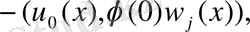
Кез келген j және
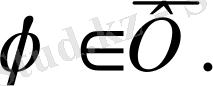 (30) -ны бөліктеп интегралдайық.
(30) -ны бөліктеп интегралдайық.
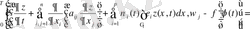
(29) -ң көмегімен кез келген j үшін
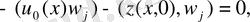 . 3 аламыз
. 3 аламыз
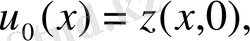 Equation. 3 яғни
Equation. 3 яғни
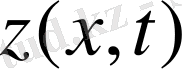 Equation. 3 (4) -(6) шектік есептің бастапқы шешімі теорема 1-де дәлелденді.
Equation. 3 (4) -(6) шектік есептің бастапқы шешімі теорема 1-де дәлелденді.
Келесі есепті қарастырайық, ол (4) -(6) есепке байланысты
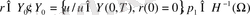 . (31)
. (31)
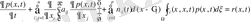
 обылысында (32)
обылысында (32)
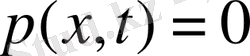
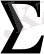 , обылысында (33)
, обылысында (33)
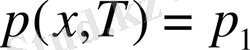 Ω, обылысында (34)
Ω, обылысында (34)
мұнда
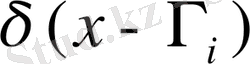 - Дирака функциясы (32) - (34) есептің шешімін дәлелдейміз.
- Дирака функциясы (32) - (34) есептің шешімін дәлелдейміз.
Теорема 1 шарты арқылы (4) - (6) есептің операторы.
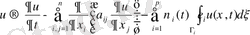 (35)
(35)
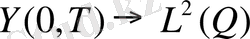 геоморфизімді анықтайды. Өйткені
геоморфизімді анықтайды. Өйткені

 . геоморфизімде орын алады. Бұдан, егер
. геоморфизімде орын алады. Бұдан, егер
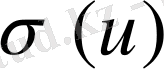 сызықты үзіліксіз формасы
сызықты үзіліксіз формасы
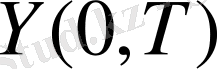 , болса, онда теорема Рисс бойынша
, болса, онда теорема Рисс бойынша
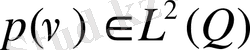 бір элементі бар, ол үшін
бір элементі бар, ол үшін
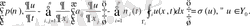 (36)
(36)
Сызықты үзіліссіз формасын берейік:
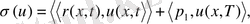 Equation. 3 (37)
Equation. 3 (37)
мұнда
 - екілік кеңістігі
- екілік кеңістігі
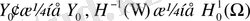 сәйкес қойылған. Онда анықтауды дұрыстауға болады.
сәйкес қойылған. Онда анықтауды дұрыстауға болады.
Теорема 2
(32) - (34) есебі кез келген
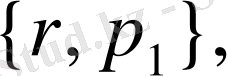 кезінде 31 - ге туындалған
кезінде 31 - ге туындалған
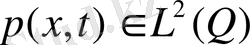 ,
бір ғана шешімі болады, және ол (36) - (37) интегралдық қасиетті қанағаттандырады. Бір
,
бір ғана шешімі болады, және ол (36) - (37) интегралдық қасиетті қанағаттандырады. Бір
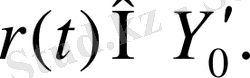 элементі бейнелеуін берейік
элементі бейнелеуін берейік
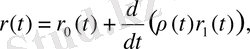
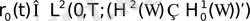 ,
,
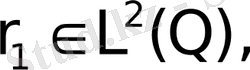
мұнда
 -ақырсыз дифференциалдық функция, анықталған; мысалы келесі түрде:
-ақырсыз дифференциалдық функция, анықталған; мысалы келесі түрде:
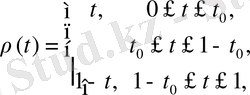
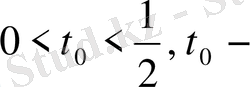 бекітілген.
бекітілген.
Шындығында (32) -(34) шектік есебі үшін (17) -(19) ұқсас келесі нәтиже дұрыс.
Теорема 3.
(7) шарты орындалсын, онда (32) -(34) есебі
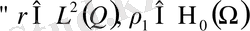 бір ғана шешімі
бір ғана шешімі
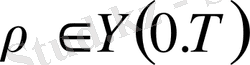 бар. Бұл шешім алғашқы мәліметтерде үзіліссіз, тәуелді, яғни
бар. Бұл шешім алғашқы мәліметтерде үзіліссіз, тәуелді, яғни
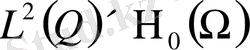 бейнелеуі
бейнелеуі
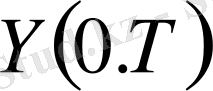 кеңістігінде үзіліссіз. Теорема 3- тің дәлелі теорема 1-ге ұқсас.
кеңістігінде үзіліссіз. Теорема 3- тің дәлелі теорема 1-ге ұқсас.
2. ТИІМДІЛІКТІҢ ЖЕТКІЛІКТІ ШАРТЫ.
2. 1 Тиімді шешімнің бар болуы.
Теорема 4. (4) -(8) тиімді басқару есебінің шешімі бар.
Дәлелдеуі
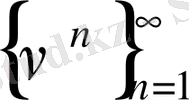 - минимизациаланған басқару тізбегі, яғни
- минимизациаланған басқару тізбегі, яғни
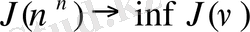
 . коэрцитоновтың функционал (8) күшімен
. коэрцитоновтың функционал (8) күшімен
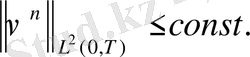 (38)
(38)
жорамал баға (4) -(6) есебі үшін:
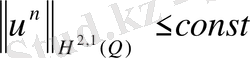 , (39)
, (39)
мұнда
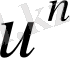 (4) -(6) есептің шешімі, басқару
(4) -(6) есептің шешімі, басқару
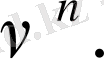
болғанда (38) -(39) шегінен шығады тізбектен басқа тізбекше алуға болады, ол
 әлсіз
әлсіз
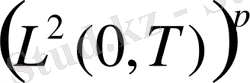 , (40)
, (40)
 әлді
әлді
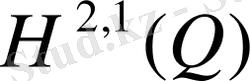 . (41)
. (41)
J з теоремасы бойынша
 әлсіз
әлсіз
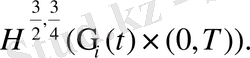 (42)
(42)
(42) -ден аламыз
 әлді
әлді
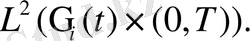 (43)
(43)
жүктелген шекті қосынды
 , ұмтылғанда
, ұмтылғанда
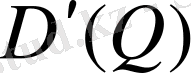 кеңістікте алатынымыз
кеңістікте алатынымыз
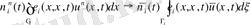 . (44)
. (44)
Расында оны келесі түрде жазып алуға болады
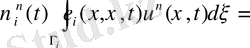
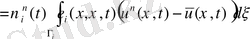 +
+
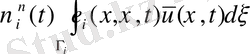
Көрсетейік
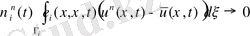 .
.
аламыз
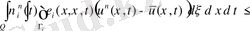
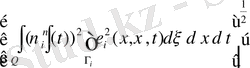
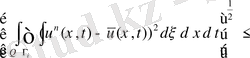
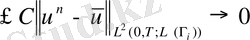 (43) көмегімен
(43) көмегімен
Өйткені (40) келесі орын алады
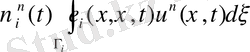
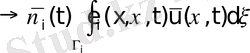 .
.
Бұдан (40-44) -дан
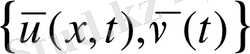 парасы (4) -(6) есебін қанағаттандырады, өйткені функционалы жай, төменнен үзіліссіз. Онда
парасы (4) -(6) есебін қанағаттандырады, өйткені функционалы жай, төменнен үзіліссіз. Онда
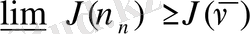 при
при
 ,
,
тізбектелген минимизация үшін
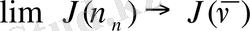 при
при
 ,
,
келесі теңдік
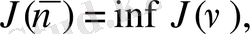 орындалады, яғни
орындалады, яғни
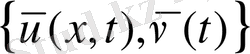 (4) -(7)
(4) -(7)
есептің шешімі. Теорема 4 дәлелденді.
2. 2 Тиімділіктің жеткілікті шарты
Тиімділіктің жеткілікті шарты (максимуму принципі), сызықты есепті қамтыған шешімді береді. Ол үшін дәлелденген алгоритмі құрастырылған. Сызықты емес есебі үшін әлі универсалдық және қатты келесі әдіс үшін жарамды сандық алгоритмі жоқ. Тиімді басқару есепті шешу тиімділіктің жеткілікті шарт теориясы. Кротов. В. Ф. берілгені бойынша есептеледі. Тиімді басқару есебінің жүйелері үшін Кротов методикасы Дженалиев Н. Т. арқылы дамыды.
Айтылған бөлімде тиімділіктің жеткілікті шарты қарастырылып, санаулы алгоритм арқылы, тиімді басқару есептің шешімі жасалынған.
Келесі белгілеулер енгізейік:
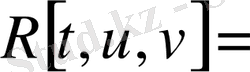 (45)
(45)
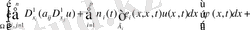
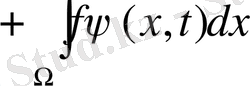
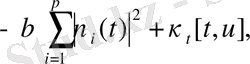
мұнда
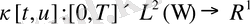 үзіліссіз дифференциалданатын функционал, осыдан
үзіліссіз дифференциалданатын функционал, осыдан
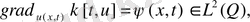 (46)
(46)
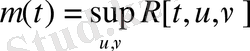 ,
,
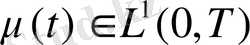 (47)
(47)
(4) -(6) шарты орындалады
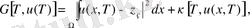 (48)
(48)
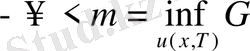 (49)
(49)
(4) -(6) шарты орындалады
Теорема 5
(45) -(49) шартын қанағаттандыратын
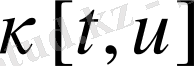 функционалы бар болсын Онда тиімділік пар үшін
функционалы бар болсын Онда тиімділік пар үшін
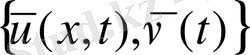 келесі шарт орындалуы қажет және жеткілікті
келесі шарт орындалуы қажет және жеткілікті
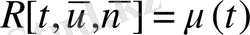 яғни
.
яғни
.
 ,
(50)
,
(50)
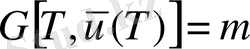 .
(51)
.
(51)
Дәлелдеу:
кез келген
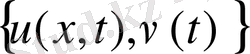 үшін аламыз
үшін аламыз
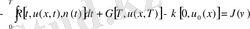 . (52)
. (52)
шындығында
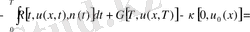
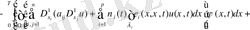
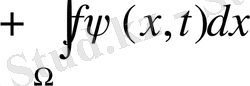
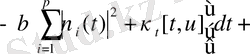
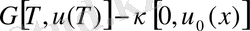 =
=
= (4) теңдеуді ескеріп =
=
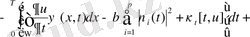
+
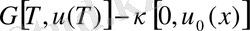 =
=
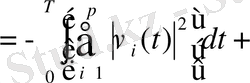
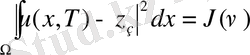 ,
,
онда
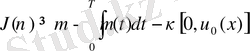 . (53)
. (53)
(53) -ші теңсіздік
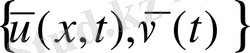 . да тиімділікке жетеді. Жеткіліктілік көрсетеді.
. да тиімділікке жетеді. Жеткіліктілік көрсетеді.
2. 3 Интерациалық алгоритм
Теорема (8) -ден белгілі әрбір конструктивтік процедура
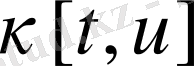 функционалын құруда қандай да бір тиімді басқару (4) -(8) есептеуі интерациалық алгоритм шешімін туғызады
функционалын құруда қандай да бір тиімді басқару (4) -(8) есептеуі интерациалық алгоритм шешімін туғызады
Келесі алгоритм беріледі
1.
бастапқы жақындау басқаруы беріледі
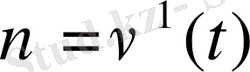 және
және
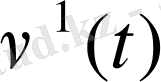 басқару берілгенде (4) -(6) шектік есептің
басқару берілгенде (4) -(6) шектік есептің
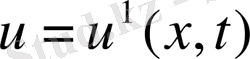 шешімі анықталады;
шешімі анықталады;
2.
(8) - функционалдық мәні
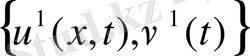 болғанда есептелінеді
болғанда есептелінеді
3.
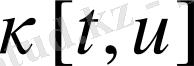 функционалы анықталады, келесі шарттардан
функционалы анықталады, келесі шарттардан
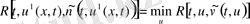 , (54)
, (54)

 (55)
(55)
4. Функционал табылады (U-ға тәуелді)
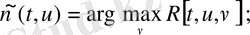 (56)
(56)
5.
(4) -(6) шектік есебі басқарылым арқылы шешіледі Ол (56) - мен анықталатын және
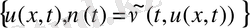 басқару үшін жаңа жақындалу табылады. Нәтижесінде
басқару үшін жаңа жақындалу табылады. Нәтижесінде
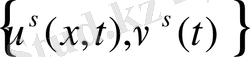
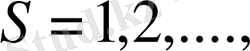 тізбектелген функция аламыз
тізбектелген функция аламыз
Бұл келесі теорема арқылы дәлелденген
Теорема 6
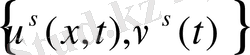 ,
тізбек үшін алынған алгоритмге келесі теңсіздік дұрыс
,
тізбек үшін алынған алгоритмге келесі теңсіздік дұрыс
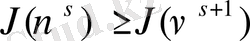 (57)
(57)
Кез келген
 үшін. Теңдік белгісі шарт орындалғанда ғана болады.
үшін. Теңдік белгісі шарт орындалғанда ғана болады.
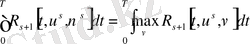
Дәлелі:
Кез келген
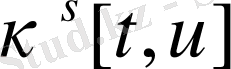 , Функционалы (45) -(49) шартын қанағаттандыратын және кез келген
, Функционалы (45) -(49) шартын қанағаттандыратын және кез келген
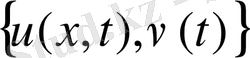 үшін келесі теңдік дұрыс
үшін келесі теңдік дұрыс
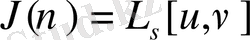 , (58)
, (58)
мұнда
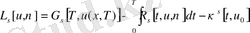 .
.
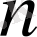 -индекісі- бұл
-индекісі- бұл
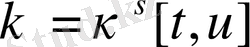 . шығарылған формула. Көрсетіп өтсек
. шығарылған формула. Көрсетіп өтсек
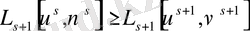 .
.
Расында (58) бойынша аламыз.
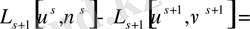
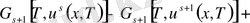
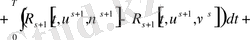
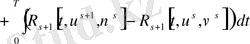 .
.
(56) арқылы келесіні шығарамыз
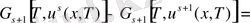
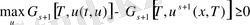 .
.
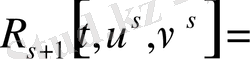
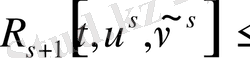
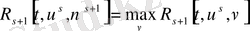
57-нің күшімен. Бұдан шығады.
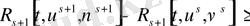
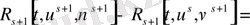
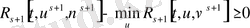
55-тің күшімен 58-теңсіздігі дәлелденді. Теңдің белгісі тек шарт орналғанда ғана қойылады.
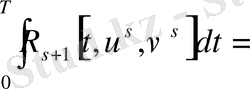
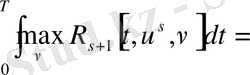
ал бұдан шығады
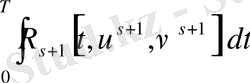
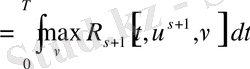 ,
,
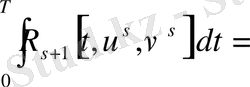
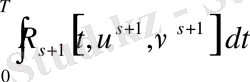 ,
,
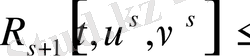
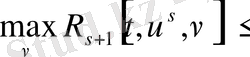
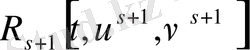 .
.
Теорема 6 дәлелденді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz