Сызықтық функционалдық теңдеулер: теориясы, Коши әдісі және дифференциалданатын функцияларға арналған шешу әдістері


Мазмұны
1 ФУНКЦИОНАЛДЫҚ ТЕҢДЕУЛЕР ТЕОРИЯСЫ ТУРАЛЫ НЕГІЗГІ ТҮСІНІКТЕР6
2 БІР ФУНКЦИЯНАЛДЫҚ ТЕҢДЕУДІ ШЕШУ. 13
2. 2 Логарифдік функция16
2. 3 Дәрежелік функция16
2. 4 Тригонометриялық және гиперболалық косинус17
3 ЕРКІН АЙНЫМАЛЫЛАРЫ БАР ФУНКЦИЯНАЛДЫҚ ТЕҢДЕУДІКОШИ ӘДІСІМЕН ШЕШУ19
4 ДИФФЕРЕНЦИЯЛДАНАТЫН ФУНКЦИЯ КЛАСЫНА ЕРКІН АЙНЫМАЛЫЛАРЫ БАР ФУНКЦИЯНАЛДЫҚ ТЕҢДЕУДІ ШЕШУ ӘДІСТЕРІ
Қорытынды
ӘДЕБИЕТТЕР ТІЗІМІ
Даламбер 1769 жылы күштердің қосылу заңын дәлелдеу кезінде
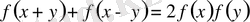 теңдеуінің шешіміне келді. 1804 жылы сол теңдеуді дәл сол мақсатпен Пуассон қарастырды, ал 1821 жылы Коши сол теңдеудің
теңдеуінің шешіміне келді. 1804 жылы сол теңдеуді дәл сол мақсатпен Пуассон қарастырды, ал 1821 жылы Коши сол теңдеудің
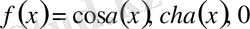 жалпы шешімдерін тапты. Коши, Лежандр мен Гаусс қарастырған
жалпы шешімдерін тапты. Коши, Лежандр мен Гаусс қарастырған
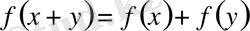 функционалдық теңдеуінің шешімін тапты.
функционалдық теңдеуінің шешімін тапты.
Лобачевский бірдей арақашықтықта орналасқан және центрлері бір нүктеде жатқан екі орицклдің доғаларының ұзындықтарының арасындағы
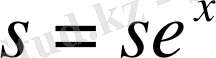 теңдеуін қорытып шығару үшін Кошидің функционалдық теңдеуін пайдаланған.
теңдеуін қорытып шығару үшін Кошидің функционалдық теңдеуін пайдаланған.
1826-1827 ж. функционалдық теңдеулермен бірнеше рет айналысқан Абель бұл пән бойынша өзінің 3 еңбегін жариялаған.
Дарбу функционалдық теңдеуді күш параллелограммасы мәселесіне және проективтік геометрияның негізгі теоремасына қолданды. 1908 жылы Шиммак функционалдық теңдеудің теоремасы мен олардың механикада қолданылуына шолу жасады. Кейбір теңдеулер Сикордың шолулық мақаласында қаралған.
Бірнеше белгісіз функциялары бар функционалдық теңдеулер Синцованың шолу мақаласында кездеседі.
Сонымен қатар белгісіз функциялары бар функцияналдық теңдеулер Сута Швейцермен, Вилсонмен және т. б. авторлармен қарастырылады.
Басқа математикалық теориядан гөрі функцияналдық теңдеу теориясында жалпы шешу әдістері аз. Бұл жағдай көбінде функцияналды теңдеудің әртүрлілігімен және зерттеу кезінде пайда болатын қиындықтармен де түсіндіріледі. Еркін айнымалылар бар және еркін айнымалылары жоқ теңдеуді шешу әдістері арасында көп айырмашылықтары бар, сондықтан да олар бөлек зерттеледі.
Біз ізделінетін функция бір айнымалы функциясы болатын еркін айнымалылары бар сызықты функцияналды теңдеумен айналысамыз.
Функционалдық теңдеу деп композициялар операциясының көмегімен белгілі функция белгісіз функциялармен байланысты болатын теңдеуді айтамыз.
Сызықты функционалдық теңдеу деп дәрежесі 1-ге тең ізделінді белгісіз функциясы бар теңдеуді айтамыз.
Құрамында еркін айнымалылар бар теңдеулер функционалдық теңдеулер деп аталады, егер тәуелсіз айнымалылар саны белгісіз функциялар санынан үлкен болса.
1 ФУНКЦИОНАЛДЫҚ ТЕҢДЕУЛЕР ТЕОРИЯСЫ ТУРАЛЫ НЕГІЗГІ ТҮСІНІКТЕР
Сандық функция деп
 ішкі жиынын
ішкі жиынын
 нақты сандар жиынының басқа
нақты сандар жиынының басқа
 ішкі жиынының
ішкі жиынының
 жиынында бейнелеуді айтады.
жиынында бейнелеуді айтады.
Мұнда
 - функцияның анықталу аймағы, ал
- функцияның анықталу аймағы, ал
 функцияның мәндердің аймағы деп аталады. Басқаша айтқанда, сандық функция - бұл
функцияның мәндердің аймағы деп аталады. Басқаша айтқанда, сандық функция - бұл
 жиынындағы әр нақты санына сәйкес
жиынындағы әр нақты санына сәйкес
 жиынынан бір сан қиылатын
жиынынан бір сан қиылатын
 заңы. Мұнда
заңы. Мұнда
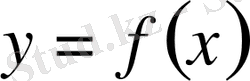 деп жазады.
деп жазады.
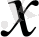 -ті аргумент немесе тәуелсіз айнымалы, ал
-ті аргумент немесе тәуелсіз айнымалы, ал
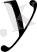 -ті функция немесе тәуелді айнымалы деп атайды.
-ті функция немесе тәуелді айнымалы деп атайды.
Көбінде функцияны
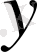 функциясының сәйкес мәндерін табу үшін
функциясының сәйкес мәндерін табу үшін
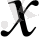 аргументіне қолданылатын амалдар көрсетіліп тұрған формула түрінде беріледі. Бұл жағдайда, функцияны аналитикалық түрде берілген деп айтады.
аргументіне қолданылатын амалдар көрсетіліп тұрған формула түрінде беріледі. Бұл жағдайда, функцияны аналитикалық түрде берілген деп айтады.
Бізге екі функция берілсін:
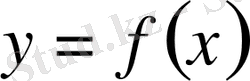 функциясы
функциясы
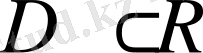 жиынын
жиынын
 жиынына бейнелейтін функция, және
жиынына бейнелейтін функция, және
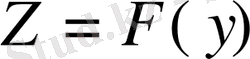 ,
,
 жиынын
жиынын
 жиынына бейнелейтін функция.
жиынына бейнелейтін функция.
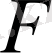 пен
пен
 функциясының немесе
функциясының немесе
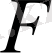 пен
пен
 функциясынан құралған күрделі функциясының композициясы деп
функциясынан құралған күрделі функциясының композициясы деп
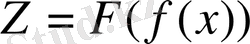 теңдеуімен табылатын және
теңдеуімен табылатын және
 жиынын
жиынын
 жиынында бейнелейтін функцияны атайды.
жиынында бейнелейтін функцияны атайды.
Мысалы,
 жиынында анықталған
жиынында анықталған
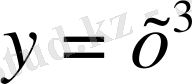 функциясы мен
функциясы мен
 жиынында жиын мәні [-1, 1] анықталған
жиынында жиын мәні [-1, 1] анықталған
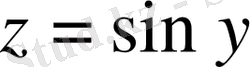 функциясының композициясы
функциясының композициясы
 жиынында жиын мәні [-1, 1] анықталған
жиынында жиын мәні [-1, 1] анықталған
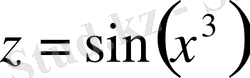 функиясы болады.
функиясы болады.
Шешу кезінде осы алмасытру әдісінің теңдеуін қолдана отырып, біз кейбір жаңа функциялармен (соның ішінде тұрақтымен де) бір немесе екі тәуелсіз айнымалыларды ауыстыра алатынымыз айқын.
Қарапайым жағдайларда тәуелсіз айнымалыны тұрақтыға ауыстыру еркін айнымалы бар функцияналды теңдеуді шешімі тез табылатын еркін айнымалысы жоқ теңдеуге әкеледі.
Сөйтіп,
 теңдеуде
теңдеуде
 деп алып, біз
деп алып, біз
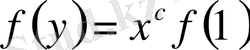 теңдігіне немесе
теңдігіне немесе
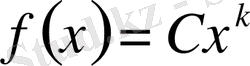 мұнда
мұнда
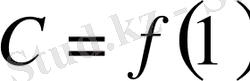 келеміз.
келеміз.
Мұнда формула тікелей тексеру арқылы бұл функцияның кез келген нақты

 теңдеуінің шешімі болатынына көз жеткізуге болады.
теңдеуінің шешімі болатынына көз жеткізуге болады.
Күрделі жағдайларда бір тәуелсіз айнымалыны тұрақтыға ауыстыру еркін айнымалысы жоқ теңдеулерге әкеледі, бірақ ол өз кезегінде алмастыру әдісімен шешілуі мүмкін.
Мысалы,
 теңдеуге
теңдеуге
 деп алып, біз
деп алып, біз
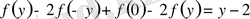
теңдеуін табамыз. Бұл теңдеуде
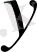 -ті
-ті
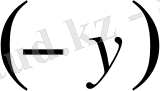 -ке ауыстырып, біз
-ке ауыстырып, біз
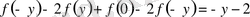 теңдеуіне келеміз.
теңдеуіне келеміз.
Соңғы екі теңдеудің бірігуі
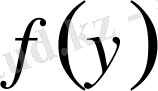 пен
пен
 белгісіз функцияларына сәйкес сызықты алгебралық теңдеулер жүйесін береді, мұнда
белгісіз функцияларына сәйкес сызықты алгебралық теңдеулер жүйесін береді, мұнда
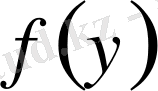 белгісіз теңдеуі былай табылады:
белгісіз теңдеуі былай табылады:
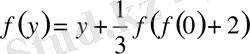 .
.
 теңдеуіне
теңдеуіне
 сүйене отырып,
сүйене отырып,
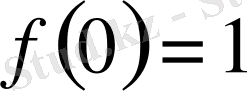 табамыз,
табамыз,
 теңдеуінің шешімі келесі функция болады:
теңдеуінің шешімі келесі функция болады:
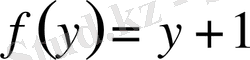 .
.
Тәуелсіз айнымалының біреуін тұрақтыға теңестіре отырып, біз белгісіз функцияның бір мәнін қарастырылуын шығарамыз. Кейде бұл мән анықталады. Мәселен
 теңдеуін шешкенде ол
теңдеуін шешкенде ол
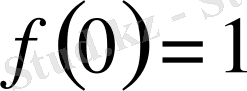 болды. Алайда кейде бұл мәнді табу мүмкін болмайды, ал мұндай жағдайда табылған шешім туынды тұрақтыға байланысты болады.
болды. Алайда кейде бұл мәнді табу мүмкін болмайды, ал мұндай жағдайда табылған шешім туынды тұрақтыға байланысты болады.
Осыған орай әр жағдайда табылған функцияның қандай мәндерінде теңдеу шешімі болатынын тексеріп отыру керек.
Мұндай өнерді бір не екі тәуелсіз айнымалының функцияларға ауыстыру кезінде аламстыруды іздеу талап етеді.
Мысал ретінде келесі теңдеуді қарастырайық:
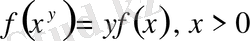
Бұл теңдеуде
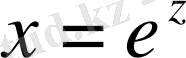 ауыстырып, біз мына теңдікке келеміз:
ауыстырып, біз мына теңдікке келеміз:
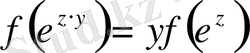 .
.
 болғанда:
болғанда:
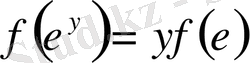 .
.
Яғни,
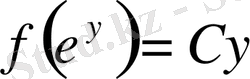 . Мұнда
. Мұнда
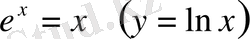 қойып, мына түрдегі теңдеу шешімін аламыз:
қойып, мына түрдегі теңдеу шешімін аламыз:
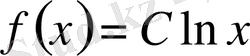 , мұнда
, мұнда
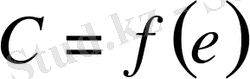 .
.
Көріп тұрғандай бұл функция кез келген
 үшін алғашқы теңдеудің шешімі болады.
үшін алғашқы теңдеудің шешімі болады.
Әрине, еркін айнымалылары бар функциялы теңдеуді шешу кезінде алмастыруды таңдау теңдеудің құрылымына байланысты болады.
Нақты түрдің аламастырылуында жіберілетін осындай теңдеудің түрлерінің саны
 жұмыста келтірілген. Солардың кейбіреулерін қарастырайық.
жұмыста келтірілген. Солардың кейбіреулерін қарастырайық.
1) Мына бір түрдің теңдеуі:
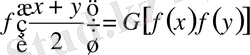 ,
,

Мұнда
 - кейбір функция, жалпылама теңдеу ретінде қарастырылады.
- кейбір функция, жалпылама теңдеу ретінде қарастырылады.
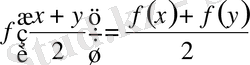

Мұндай теңдеулер
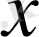 -ті
-ті
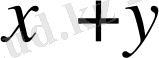 -ке, ал
-ке, ал
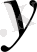 -ті
-ті
 -ге ауыстыру жолы арқылы жай түрге келтіріледі. Бұл алмастыруларды
-ге ауыстыру жолы арқылы жай түрге келтіріледі. Бұл алмастыруларды
 теңдеуіне қолданайық. Нәтижесінде мына теңдеуді аламыз.
теңдеуіне қолданайық. Нәтижесінде мына теңдеуді аламыз.
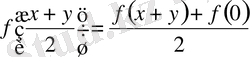

 пен
пен
 теңдеулердің оң жақ бөліктерін теңестіру арқылы келесі теңдеуге келеміз:
теңдеулердің оң жақ бөліктерін теңестіру арқылы келесі теңдеуге келеміз:
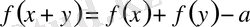 ,
,
Мұнда
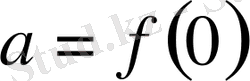 .
.
Соңғы теңдікті
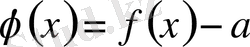 алмасытыру кезінде Коши теңдеуіне ауысады:
алмасытыру кезінде Коши теңдеуіне ауысады:
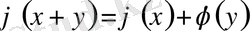 ,
,
оның шешімі
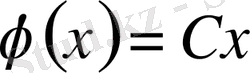
және
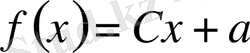 болады.
болады.
2) Мына түрдегі теңдеу:
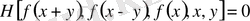

Мұнда
 - қандайда бір теңдеу.
- қандайда бір теңдеу.
Оған екі тәсіл көрсетеміз, әр тәсілге
 - функциясына байланысты аламстырулар қолданылады. Осы тәсілдердің біріншісін мына мысалда төмендегі теңдеумен көрсетеміз:
- функциясына байланысты аламстырулар қолданылады. Осы тәсілдердің біріншісін мына мысалда төмендегі теңдеумен көрсетеміз:
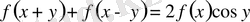

 теңдеуіне үш алмастыру жүргіземіз:
теңдеуіне үш алмастыру жүргіземіз:
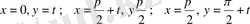 және
және
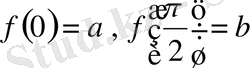 белгілеулерін енгіземіз.
белгілеулерін енгіземіз.
Нәтижесінде үш теңдеу аламыз:
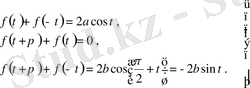
Бұл
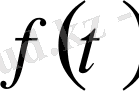 ,
,
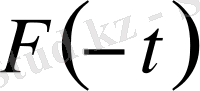 және
және
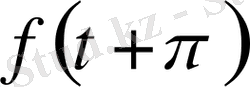 үш белгісізден құралған үш алгебралық теңдеудің жүйесі.
үш белгісізден құралған үш алгебралық теңдеудің жүйесі.
Жүйенің алғашқы екі теңдеуін қосып, шыққан қосындымен үшінші теңдеуді есептеп,
 белгісіз функциясын табамыз.
белгісіз функциясын табамыз.
Тікелей тексеру бұл функцияның кез келген
 мен
мен
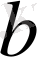
 теңдеуінің шешімі болатынын көрсетеді. Мысалды қарастырғанда,
теңдеуінің шешімі болатынын көрсетеді. Мысалды қарастырғанда,
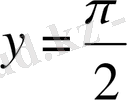 үшін
үшін
 фукциясының тепе-теңдігі 0-ге айналады. Сондықтан да, осы әдістің
фукциясының тепе-теңдігі 0-ге айналады. Сондықтан да, осы әдістің
 түрдегі теңдеу сияқты таралуы үшін
түрдегі теңдеу сияқты таралуы үшін
 мәні болуы керек, ал ол үшін
мәні болуы керек, ал ол үшін
 теңдеудегі
теңдеудегі
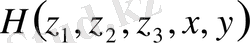 функциясы
функциясы
 -тен тәулсіз болуы керек.
-тен тәулсіз болуы керек.
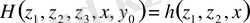
мұнда,
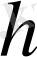 -қандай да бір функция.
-қандай да бір функция.
Егр бұл шарт орындалса, онда келесі аналогиялық әдіс шешімді табуға көмектеседі.
 теңдеуінде
теңдеуінде

алмастыруларын жасай отырып, және
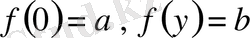 белгілерін енгізе отырып, біз келесі теңдеулерді аламыз:
белгілерін енгізе отырып, біз келесі теңдеулерді аламыз:
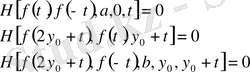

Осы теңдеуден
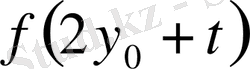 мен алу арқылы ізделетін
мен алу арқылы ізделетін
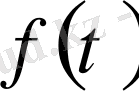 функциясын аламыз.
функциясын аламыз.
Егер,
 шарты орындалмаса, онда келесі тәсілді қолдануға болады.
шарты орындалмаса, онда келесі тәсілді қолдануға болады.
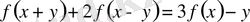 теңдеуін қарастырамыз.
теңдеуін қарастырамыз.
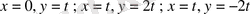 алмастыруларын орындай отрып, осыған
алмастыруларын орындай отрып, осыған
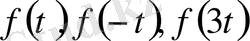 белгісіздеріне қатысты алгебралық теңдеулерді аламыз:
белгісіздеріне қатысты алгебралық теңдеулерді аламыз:
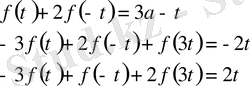
Осыдан
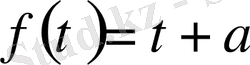 табамыз, мұнда
табамыз, мұнда
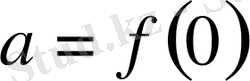 . Бұл функция берілген теңдеуді кез келген
. Бұл функция берілген теңдеуді кез келген
 нақты тұрақтысында қанағаттандырады.
нақты тұрақтысында қанағаттандырады.
Сипатталған тәсілді жалпы теңдеуге
 қолданамыз. Шынында да,
қолданамыз. Шынында да,
 теңдеуінде
теңдеуінде
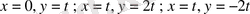 алматыруды орындай отырып,
алматыруды орындай отырып,
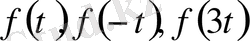 белгісіздеріне қатысты үш теңдеудің жүйесін аламыз:
белгісіздеріне қатысты үш теңдеудің жүйесін аламыз:
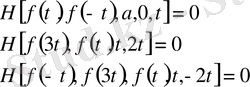
Егер бұл жүйе шешілетін болса, онда
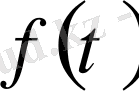 белгісіз функциясы табылады.
белгісіз функциясы табылады.
3) Мына түрдегі теңдеу,
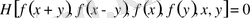

Мұнда
 - қандай да бір функия.
- қандай да бір функия.
 теңдеуі үшін төмендегі 4 алмастыруды орындайық:
теңдеуі үшін төмендегі 4 алмастыруды орындайық:
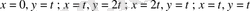
Бұл бізге белгісіздері
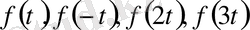 болатын 4 теңдеудің жүйесін береді. Егер алынған жүйе шешілетін болса, онда біз
болатын 4 теңдеудің жүйесін береді. Егер алынған жүйе шешілетін болса, онда біз
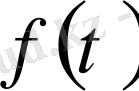 белгісіз фунциясын табамыз.
белгісіз фунциясын табамыз.
Мысалы, мына теңдеуді қарастырайық:
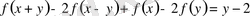
Көрсетілген алмастырулар арқылы осы теңдеуден 4 сызықты алгебралық теңдеудің жүйесін аламыз:
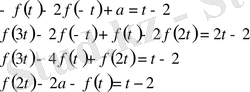
Мұнда
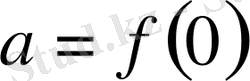
Бірінші мен үшінші теңдеудің қосындысынан үшке көбейтілген төртінші және екінші теңдеуді есептеп:
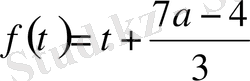
немесе қысқаша,
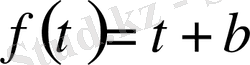 табамыз. Мұнда
табамыз. Мұнда
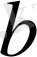 тұрақты.
тұрақты.
Алайда тікелей алмастыру арқылы
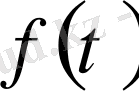 функциясы
функциясы
 болғанда ғана теңдеуді қанағаттандыра алады. Сонда,
болғанда ғана теңдеуді қанағаттандыра алады. Сонда,
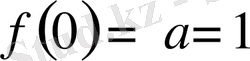 үшін
үшін
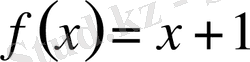 шешімі болуы мүмкін.
шешімі болуы мүмкін.
 теңдеуіне жалпы жағдайда
теңдеуіне жалпы жағдайда
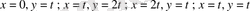 алмастыруларын жүргізуге болады. Нәтижесінде
алмастыруларын жүргізуге болады. Нәтижесінде
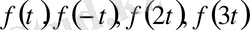 белгісіз функцияларына қатысты төрт теңдеудің жүйесін аламыз:
белгісіз функцияларына қатысты төрт теңдеудің жүйесін аламыз:
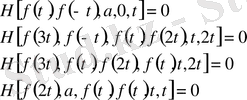
мұнда
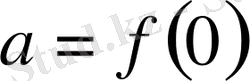 .
.
Егер бұл жүйе шешілсе, онда
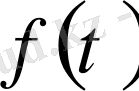 белгісіз функциясы да табылады.
белгісіз функциясы да табылады.
2 БІР ФУНКЦИЯНАЛДЫҚ ТЕҢДЕУДІ ШЕШУ.
Анықтама:
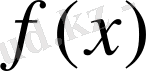 функциясы
функциясы
 нүктесінде үзіліссіз болады, егер келесі қатынас орындалса:
нүктесінде үзіліссіз болады, егер келесі қатынас орындалса:
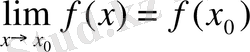 .
.
Есепті шешейік:
Кез-келген
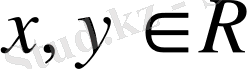 болғанда
болғанда
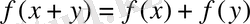
 .
.
 шартын қанағаттандыратын
шартын қанағаттандыратын
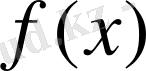 функциясының
функциясының
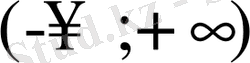 аралығындағы барлық үзіліссіздіктерін табу керек.
аралығындағы барлық үзіліссіздіктерін табу керек.
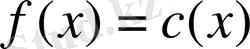

 .
.
 түріндегі біртекті сызықтық функциялар
түріндегі біртекті сызықтық функциялар
 теңдеуін қанағаттандырады.
теңдеуін қанағаттандырады.
Бұл функциялардың
 теңдеуінің қасиеті бар жалғыз үзіліссіз функциялар болатынын дәлелдейік.
теңдеуінің қасиеті бар жалғыз үзіліссіз функциялар болатынын дәлелдейік.
Қандай да бір үздіксіз
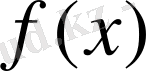 функциясы
функциясы
 теңдеуін қанағанттандырады делік, сонда ол
теңдеуін қанағанттандырады делік, сонда ол
 теңдеуінің түрінде болатынын көрсетейік.
теңдеуінің түрінде болатынын көрсетейік.
Математикалық индукция әдісінің көмегімен
 қатынасын кез-келген
қатынасын кез-келген
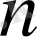 -қосылғыштар санына жалпылаймыз:
-қосылғыштар санына жалпылаймыз:
1.
 болсын,
болсын,
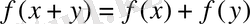
2. Ол
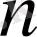 -қосылғыштар үшін де орынды деп ұйғарайық,
-қосылғыштар үшін де орынды деп ұйғарайық,
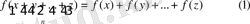
3.
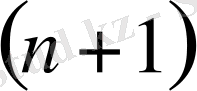 -қосылғыштар үшін орынды болатынын дәлелдейік.
-қосылғыштар үшін орынды болатынын дәлелдейік.
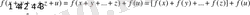
 теңдеуде
теңдеуде
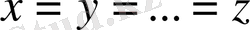 болсын, онда
болсын, онда
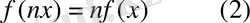
Егер
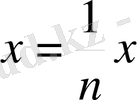 , онда
, онда
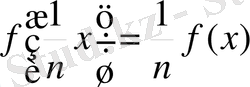 .
.
Егер
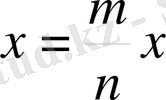 , онда
, онда
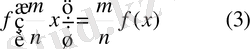
Егер
 теңдеуінде
теңдеуінде
 болса, онда
болса, онда
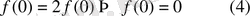
Егер
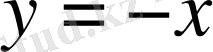 болса, онда
болса, онда
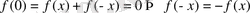
Онда
 мен
мен


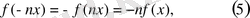
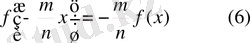
 -
-
 қатынастарын келесі теңдікке біріктіруге болады:
қатынастарын келесі теңдікке біріктіруге болады:
Кез-келген
 және
және
 үшін
үшін
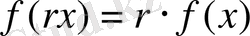 .
.
Егер
 деп алып,
деп алып,
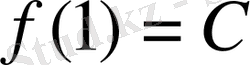 деп белгілесек, онда
деп белгілесек, онда
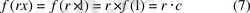
Сөйтіп, функцияның үзіліссіздігін пайдаландай, функцияның
 теңдеуін қанағаттандыратынын қолданып,
теңдеуін қанағаттандыратынын қолданып,
 функциясының түрін тек аргументтің рационал мәндері үшін ғана шығардық.
функциясының түрін тек аргументтің рационал мәндері үшін ғана шығардық.
Енді
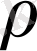 аргументтің кез-келген иррационалды мәні болсын.
аргументтің кез-келген иррационалды мәні болсын.
Рационал сандар тізбегі
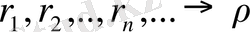 .
.
 қолдана отырып,
қолдана отырып,
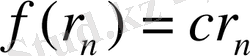 шығарамыз, мұнда
шығарамыз, мұнда
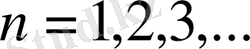
Сонда
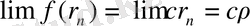
 функциясының үздіксіздігін пайдаланып,
функциясының үздіксіздігін пайдаланып,
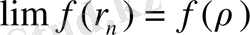 аламыз.
аламыз.
Онда
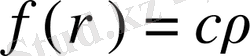 .
.
Сонымен,
 функциясы
функциясы
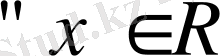 болғанда үздіксіз функциялардағы
болғанда үздіксіз функциялардағы
 теңдеуінің жалпы шешімін беретін
теңдеуінің жалпы шешімін беретін
 формуласымен көрсетіледі.
формуласымен көрсетіледі.
Функцияның функционалдық қасиетін қарастырайық.
2. 1 Көрсеткіштік функция
Егер
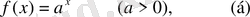 болса, онда әдетте дәрежелердің көбейтіндісін
болса, онда әдетте дәрежелердің көбейтіндісін
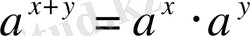 білдіретін
білдіретін
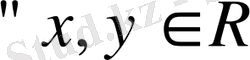 болғанда
болғанда
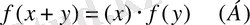 . Сонымен, жалғыз анықтарлған және
. Сонымен, жалғыз анықтарлған және
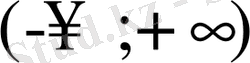 аралығында үзіліссіз және
аралығында үзіліссіз және
 шартын қанағаттандыратын функция көрсеткіштік функция (
шартын қанағаттандыратын функция көрсеткіштік функция (
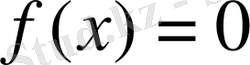 басқалары) болып табылады, яғни
басқалары) болып табылады, яғни
 формуласы үзіліссіз функцияларда
формуласы үзіліссіз функцияларда
 функциялық теңдеуінің жалпы шешімін береді.
функциялық теңдеуінің жалпы шешімін береді.
Дәлелдеуі:
Кез-келген
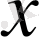 мәнінде үзіліссіз және анықталған және
мәнінде үзіліссіз және анықталған және
 шартын қанағаттандыратын кез-келген
шартын қанағаттандыратын кез-келген
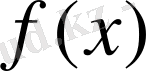 функциясын қарастырайық.
функциясын қарастырайық.
 болғанда,
болғанда,
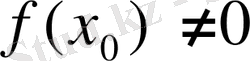 .
.
Егер
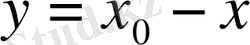 болса, онда кез-келген
болса, онда кез-келген
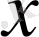 үшін
үшін

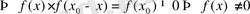 .
.
Егер
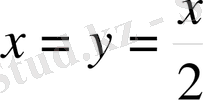 болса, онда
болса, онда
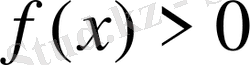 болатындай (Б)
болатындай (Б)
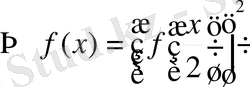 .
.
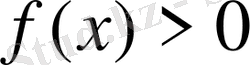 екендігін пайдаланып,
екендігін пайдаланып,
 теңдігін логарифмдейік:
теңдігін логарифмдейік:
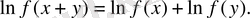
Егер
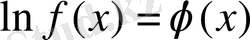 болса, онда
болса, онда
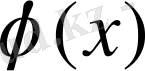 - үзіліссіз (үзіліссіз функциялардың суперпозиция нәтижесі ретінде) және келесі шартты қанағаттандыратын функция:
- үзіліссіз (үзіліссіз функциялардың суперпозиция нәтижесі ретінде) және келесі шартты қанағаттандыратын функция:
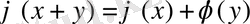 ,
,
 теңдеуіне сәйкес.
теңдеуіне сәйкес.
Онда,
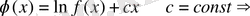
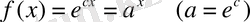 .
.
2. 2 Логарифдік функция
Егер
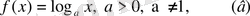
болса, онда кез-келген
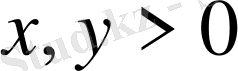 болғанда әдетте, логарифмдік туындыны
болғанда әдетте, логарифмдік туындыны
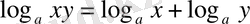 білдіретін
білдіретін
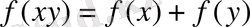 болады.
болады.
Сөйтіп, жалғыз анықталған және
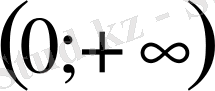 аралығында үздіксіз және
аралығында үздіксіз және
 шартын қанағаттандыратын логарифмдік функция (
шартын қанағаттандыратын логарифмдік функция (
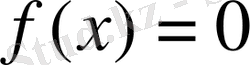 басқа) болып табылады, сондықтан
басқа) болып табылады, сондықтан
 формуласы үздіксіз функцияларда
формуласы үздіксіз функцияларда
 функциялар теңдеуінің жалпы шешімін береді.
функциялар теңдеуінің жалпы шешімін береді.
Дәлелдеуі:
 үшін үздіксіз және және осы теңдеуді қанағаттандыратын кез-келген
үшін үздіксіз және және осы теңдеуді қанағаттандыратын кез-келген
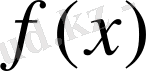 функциясын аламыз.
функциясын аламыз.
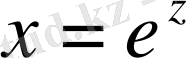 ,
,
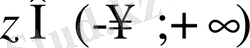 болсын, онда
болсын, онда
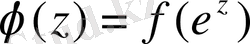 , бұдан,
, бұдан,
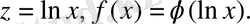
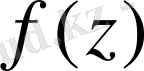 үздіксіз функциясы
үздіксіз функциясы
 теңдеуіндегідей
теңдеуіндегідей
 шартын қанағаттандырады:
шартын қанағаттандырады:
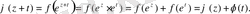
Яғни,
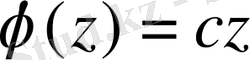 және
және
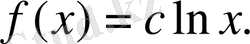
Сонымен,
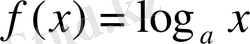 мұнда
мұнда
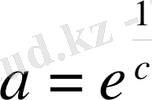 (
(
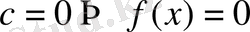 басқа) .
басқа) .
2. 3 Дәрежелік функция
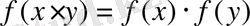
 функционалдық теңдеуді (кез-келген оң
функционалдық теңдеуді (кез-келген оң
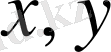 ) қанағаттандыратын, өйткені
) қанағаттандыратын, өйткені
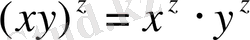 ,
,
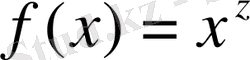
 функциясын қарастырайық.
функциясын қарастырайық.
Сөйтіп,
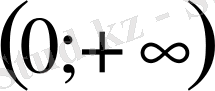 аралығында анықталған, үздіксіз және
аралығында анықталған, үздіксіз және
 шартын қанағаттандыратын жалғыз ғана функция ол дәрежелік функция болып табылады.
шартын қанағаттандыратын жалғыз ғана функция ол дәрежелік функция болып табылады.
Дәлелденуі:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz