Кинематика: материалдық нүкте, қозғалыс түрлері, жылдамдық және үдеу


- Кинематиканың негізгі ұғымдары
Кинематика деп денелердің қозғалысын зерттейтін, бірақ қозғалыстың туу себебін қарастырмайтын физиканың бөлімі.
Механикалық қозғалыс деп уақыт өзгерісінде кеңістікте дененің басқа денелерге қатысты орын ауыстыруын айтамыз.
Механикалық қозғалыс - салыстырмалы. Бір дененің әр түрлі денелерге қатысты қозғалысы әр түрлі болады. Дененің қозғалысын сипаттау үшін, қозғалыс қай денеге қатысты қарастырылатынын белгілеу қажет. Бұл денені санақ денесі деп атайды. Санақ денесі және уақыт - санақ жүйесін құрап, ол қозғалған дененің кез келген уақыттағы орнын анықтауға мүмкіндік береді.
Халықаралық бірліктер жүйесінде (СИ) ұзындықтың бірлігі ретінде метр , ал уақыттың бірлігі ретінде - секунд қабылданған.
 Әрбір дене белгілі бір өлшемдерге ие. Дененің әр түрлі бөліктері кеңістіктің әр түрлі жерлерінде орналасады. Алайда, механиканың көпшілік есептерінде дененің әр түрлі бөліктерінің орнын көрсетудің қажеті жоқ. Егер дененің өлшемдері басқа денелерге дейінгі арақашықтығынан аз болса, онда бұл денені оның
материалдық нүктесі
деп санауға болады. Мәселен, оны ғаламшарлардың Күннің айналасындағы қозғалысын зерттегенде алуға болады. Егер дененің барлық бөліктері бірдей қозғалса, ондай қозғалысты
ілгерілемелі
қозғалыс деп аталады. Мысалы үшін, «Гиганттық дөңгелек» аттракционындағы кабиналар, жолдың түзу сызықтық бөлігіндегі автомобиль және басқалар ілгерілемелі қозғалады. Дененің ілгерілемелі қозғалысында оны материалдық нүкте ретінде қарастыруға болады.
Әрбір дене белгілі бір өлшемдерге ие. Дененің әр түрлі бөліктері кеңістіктің әр түрлі жерлерінде орналасады. Алайда, механиканың көпшілік есептерінде дененің әр түрлі бөліктерінің орнын көрсетудің қажеті жоқ. Егер дененің өлшемдері басқа денелерге дейінгі арақашықтығынан аз болса, онда бұл денені оның
материалдық нүктесі
деп санауға болады. Мәселен, оны ғаламшарлардың Күннің айналасындағы қозғалысын зерттегенде алуға болады. Егер дененің барлық бөліктері бірдей қозғалса, ондай қозғалысты
ілгерілемелі
қозғалыс деп аталады. Мысалы үшін, «Гиганттық дөңгелек» аттракционындағы кабиналар, жолдың түзу сызықтық бөлігіндегі автомобиль және басқалар ілгерілемелі қозғалады. Дененің ілгерілемелі қозғалысында оны материалдық нүкте ретінде қарастыруға болады.
Сурет 1. 1. 1.
Нүктенің орнын
x
=
x
(
t
),
y
=
y
(
t
) және
z
=
z
(
t
) координаталары және
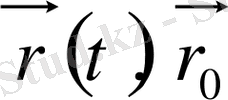 радиус-векторы арқылы анықтау.
радиус-векторы арқылы анықтау.
Радиус вектор уақыттың бастапқы кезіндегі нүктенің орны.
Өлшемдерін берілген жағдайда ескермеуге болатын денені материалдық нүкте деп атайды.
Материалдық нүкте ұғымы механикада маңызды орын алады. Уақыт өткенде бір нүктеден екінші нүктеге орын ауыстырғанда, дене (материалдық нүкте) дене қозғалысының траекториясы деп аталатын қандай да бір қисықты сызады.
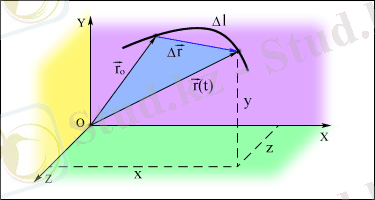
Дененің кез келген уақыттағы кеңістікте орнын ( қозғалыс заңын ) x = x ( t ), y = y ( t ), z = z ( t ) координаттардың уақыттан тәуелділігінен (координаттық әдіс), не болмаса уақыттың бастапқы нүктеден берілген нүктеге жүргізілген радиус-вектордан тәуелділігінен (векторлық әдіс) анықтауға болады (сурет 1. 1. 1) .
Дененің орын ауыстыруы
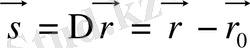 деп дененің бастапқы орнын оның кейінгі орнымен қосатын бағытталған кесіндіні айтады. Орын ауыстыру - векторлық шама.
деп дененің бастапқы орнын оның кейінгі орнымен қосатын бағытталған кесіндіні айтады. Орын ауыстыру - векторлық шама.
Жүрген жолы
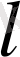 - дененің белгілі t уақыттың ішінде траектория доғасының ұзындығына тең болады.
Жол - скалярлық шама
.
- дененің белгілі t уақыттың ішінде траектория доғасының ұзындығына тең болады.
Жол - скалярлық шама
.
Егер дененің қозғалысын жеткілікті аз уақыттың ішінде қарастырса, онда орын ауыстыру векторы осы нүктеге жүргізілген траекторияның жанамасы бойымен бағытталады, ал оның ұзындығы жүрілген жолына тең болады.
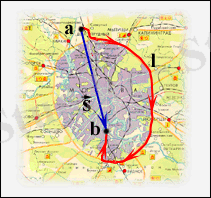 Сурет 1. 1. 2.
Қисық сызықты қозғалыстағы дененің жүрген жолы
l
және
Сурет 1. 1. 2.
Қисық сызықты қозғалыстағы дененің жүрген жолы
l
және
орын ауыстыру векторы
 .
a
және
b
- жолдың бастапқы және соңғы нүктелері.
.
a
және
b
- жолдың бастапқы және соңғы нүктелері.
Δt уақыты жеткілікті аз болған жағдайда, Δ l дененің жүрген жолы Δs орын ауыстыру векторының модулімен сәйкес келеді. Дене қисық сызықты траекторияның бойымен қозғалғанда, орын ауыстыру векторының модулі жүрген жолынан әрқашан аз болады (сурет 1. 1. 2) .
Қозғалысты сипаттау үшін
орташа жылдамдық
ұғымы енгізіледі:
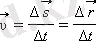
Физикада орташа жылдамдық емес, лездік уақыт қызығушылық тудырады. Ол шексіз аз Δ t уақыт ішіндегі орташа жылдамдық ұмтылғандағы шекпен анықталады:
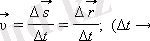
Математикада мұндай шекті
туынды
деп атап,
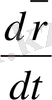 немесе
немесе
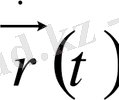 деп белгілейді.
деп белгілейді.
 Дененің қисық сызықты траекториясының кез келген нүктесіндегі
Дененің қисық сызықты траекториясының кез келген нүктесіндегі
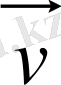 лездік жылдамдығы
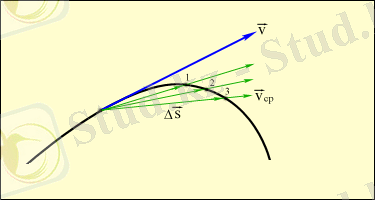
осы нүктеде траекторияға жүргізілген жанаманың бойымен бағытталады. Орташа және лездік жылдамдықтардың арасындағы айырмашылық 1. 1. 3 суретінде көрсетілген.
лездік жылдамдығы
осы нүктеде траекторияға жүргізілген жанаманың бойымен бағытталады. Орташа және лездік жылдамдықтардың арасындағы айырмашылық 1. 1. 3 суретінде көрсетілген.
Сурет 1. 1. 3 . Орташа және лездік жылдамдық.
 - бұл сәйкес
- бұл сәйкес
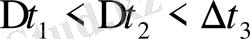 уақыт ішіндегі орын ауыстырулар.
уақыт ішіндегі орын ауыстырулар.
 кезде
кезде
 .
.
Дене қисық сызықтық траекторияның бойымен қозғалғанда, оның
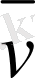 жылдамдығының модулі және бағыты өзгереді.
жылдамдығының модулі және бағыты өзгереді.
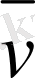 жылдамдығының қандай да бір жеткілікті аз Δt уақыты ішінде өзгерісін
жылдамдығының қандай да бір жеткілікті аз Δt уақыты ішінде өзгерісін
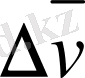 векторы арқылы беруге болады (сурет 1. 1. 4) .
векторы арқылы беруге болады (сурет 1. 1. 4) .
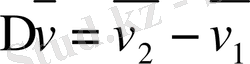 жылдамдықтың Δt уақыт ішіндегі өзгеру векторын екі құраушыға жіктеуге болады:
жылдамдықтың Δt уақыт ішіндегі өзгеру векторын екі құраушыға жіктеуге болады:
 векторының бойымен бағытталған
векторының бойымен бағытталған
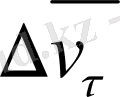 векторына (жанама құраушы) және
векторына (жанама құраушы) және
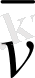 векторына перпендикуляр бағытталған
векторына перпендикуляр бағытталған
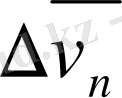 (нормаль құраушы) .
(нормаль құраушы) .
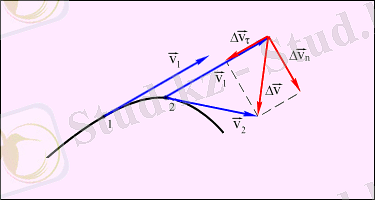 Сурет 1. 1. 4
. Жылдамдық векторының модулі және бағыты жағынан өзгеруі.
Сурет 1. 1. 4
. Жылдамдық векторының модулі және бағыты жағынан өзгеруі.
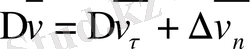 - жылдамдық векторының Δt уақытының ішінде өзгеруі.
- жылдамдық векторының Δt уақытының ішінде өзгеруі.
Дененің лездік үдеуі
(немесе
үдеу
)
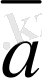 деп жылдамдықтың аз өзгеруінің
деп жылдамдықтың аз өзгеруінің
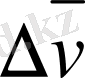 сол жылдамдық өзгерген уақыттың аз өзгеруіне Δt қатынасының шегін айтамыз.
сол жылдамдық өзгерген уақыттың аз өзгеруіне Δt қатынасының шегін айтамыз.
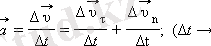
Қисық сызықты қозғалыс кезінде
 үдеу векторының бағыты
үдеу векторының бағыты
 жылдамдық векторының бағытымен сәйкес келмейді.
жылдамдық векторының бағытымен сәйкес келмейді.
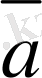 үдеу векторының құраушыларын
жанама (тангенциал)
үдеу векторының құраушыларын
жанама (тангенциал)
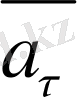 және
нормаль
және
нормаль
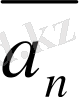 үдеу деп атайды (сурет 1. 1. 5) .
үдеу деп атайды (сурет 1. 1. 5) .
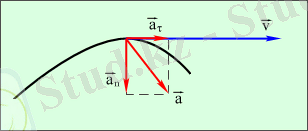 Сурет 1. 1. 5. Жанама және нормаль үдеулер.
Сурет 1. 1. 5. Жанама және нормаль үдеулер.
Жанама үдеу
дененің жылдамдығы модуль жағынан қалай өзгеретінін көрсетеді:
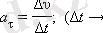
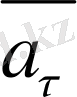 векторы траекторияға жанама бойымен бағытталады.
векторы траекторияға жанама бойымен бағытталады.
Нормаль үдеу дененің жылдамдығы бағыты жағынан қалай өзгеретінін көрсетеді. Қисық сызықты қозғалысты шеңберлер доғаларының бойымен қозғалыс түрінде көрсетуге болады (сурет 1. 1. 6) .
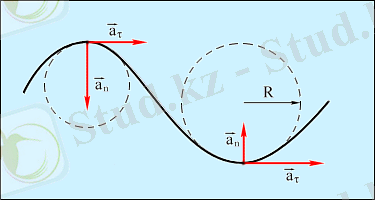 Сурет 1. 1. 6 Шеңберлер доғаларының бойымен қозғалыс.
Сурет 1. 1. 6 Шеңберлер доғаларының бойымен қозғалыс.
Нормаль үдеу v жылдамдықтың модулінен және дене осы уақытта қозғалған шеңбердің R радиусынан тәуелді.
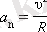
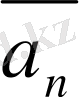 векторы әрқашан шеңбердің центріне бағытталады.
векторы әрқашан шеңбердің центріне бағытталады.
1. 1. 5. суретінен толық үдеудің модулі
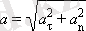 шамасына тең болатыны көрініп тұр.
шамасына тең болатыны көрініп тұр.
Сонымен, кинематикада материалдық нүктенің негізгі физикалық шамаларының қатарына:
l
жүрген жолы, Δs орын ауыстыруы,
 жылдамдық және
жылдамдық және
 үдеу жатады.
l
жолы - скаляр шама болып табылады. Δs орын ауыстыруы,
үдеу жатады.
l
жолы - скаляр шама болып табылады. Δs орын ауыстыруы,
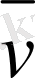 жылдамдығы және
жылдамдығы және
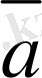 үдеу - векторлық шамаларға жатады. Векторлық шаманы көрсету үшін, оның модулін және бағытын көрсету қажет. Векторлық шамалар белгілі математикалық ережелерге бағынады. Векторларды координат осьтеріне проекциялауға, оларды қосуға, алуға, т. с. с. болады.
үдеу - векторлық шамаларға жатады. Векторлық шаманы көрсету үшін, оның модулін және бағытын көрсету қажет. Векторлық шамалар белгілі математикалық ережелерге бағынады. Векторларды координат осьтеріне проекциялауға, оларды қосуға, алуға, т. с. с. болады.
- Қозғалыстың салыстырмалылығы
Денелердің қозғалысын әр түрлі санақ жүйелерінде сипаттауға болады. Кинематиканың көзқарасы бойынша, барлық санақ жүйелері тең құқылы. Алайда, траектория, орын ауыстыру, жылдамдық сияқты қозғалыстың кинематикалық сипаттамалары әрбір жүйеде әр түрлі болады. Есептеулер жүргізілетін санақ жүйесінің таңдауынан тәуелді шамалар - салыстырмалы шамалар деп аталады.
Екі санақ жүйесі бар болсын. XOY жүйесі шартты қозғалмайтын, ал X’O’Y’ жүйесі XOY жүйесіне қатысты
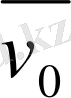 жылдамдығымен ілгерілемелі қозғалатын болсын. Мысалы үшін, XOY жүйесі Жермен, ал X’O’Y’ жүйесі - рельс бойымен қозғалып келе жатқан платформамен байланысты болуы мүмкін (1. 2. 1. сурет) .
жылдамдығымен ілгерілемелі қозғалатын болсын. Мысалы үшін, XOY жүйесі Жермен, ал X’O’Y’ жүйесі - рельс бойымен қозғалып келе жатқан платформамен байланысты болуы мүмкін (1. 2. 1. сурет) .
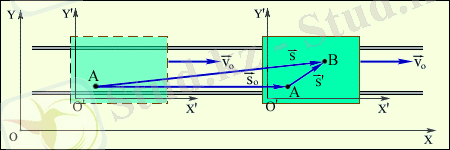 1. 2. 1. сурет. Орын ауыстыруларды әр түрлі санақ жүйелеріне қатысты қосу.
1. 2. 1. сурет. Орын ауыстыруларды әр түрлі санақ жүйелеріне қатысты қосу.
Адам платформа бойымен белгілі уақыт ішінде А нүктесінен В нүктесіне жүріп өтсін. Онда оның платформаға қатысты орын ауыстыруы
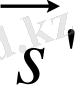 , ал платформаның Жерге қатысты орын ауыстыруы
, ал платформаның Жерге қатысты орын ауыстыруы
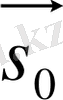 векторына сәйкес келеді. 1. 2. 1 суретінен: адамның Жерге қатысты орын ауыстыруы
векторына сәйкес келеді. 1. 2. 1 суретінен: адамның Жерге қатысты орын ауыстыруы
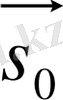 және
және
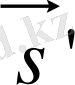 векторларының қосындысынан тұратын
векторларының қосындысынан тұратын
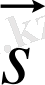 векторына тең болатынын көреміз.
векторына тең болатынын көреміз.
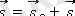 Егер санақ жүйелерінің біреуі екіншісіне қатысты 1. 2. 1. суретте көрсетілгендей тұрақты
Егер санақ жүйелерінің біреуі екіншісіне қатысты 1. 2. 1. суретте көрсетілгендей тұрақты
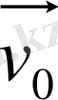 жылдамдығымен
ілгерілемелі
қозғалатын болса, онда бұл өрнек
жылдамдығымен
ілгерілемелі
қозғалатын болса, онда бұл өрнек
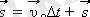 түріне келеді.
түріне келеді.
Егер қозғалысты кішкентай Δt уақыттың ішінде қарастырса, онда осы теңдеудің екі жағын Δt-ға бөліп,
 болғандағы шекке көшсек:
болғандағы шекке көшсек:
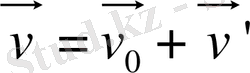 (*) аламыз. Мұндағы
(*) аламыз. Мұндағы
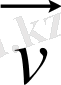 - дененің XOY «қозғалмайтын» санақ жүйесіндегі жылдамдығы,
- дененің XOY «қозғалмайтын» санақ жүйесіндегі жылдамдығы,
 - дененің X’O’Y’ «қозғалмалы» санақ жүйесіндегі жылдамдығы.
- дененің X’O’Y’ «қозғалмалы» санақ жүйесіндегі жылдамдығы.
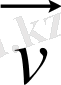 және
және
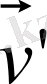 жылдамдықтары абсолют және салыстырмалы жылдамдықтар деп, ал
жылдамдықтары абсолют және салыстырмалы жылдамдықтар деп, ал
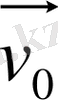 жылдамдығын - тасымал жылдамдығы деп атайды. (*) қатынасы
жылдамдықтарды қосудың классикалық заңын
өрнектейді.
жылдамдығын - тасымал жылдамдығы деп атайды. (*) қатынасы
жылдамдықтарды қосудың классикалық заңын
өрнектейді.
Дененің
абсолют
жылдамдығы
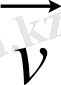 оның салыстырмалы
оның салыстырмалы
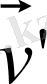 жылдамдығының және қозғалмалы санақ жүйесінің
тасымал
жылдамдығының және қозғалмалы санақ жүйесінің
тасымал
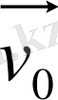 жылдамдығының векторлық қосындысына тең болады.
жылдамдығының векторлық қосындысына тең болады.
 Дененің әр түрлі санақ жүйелеріндегі үдеулеріне назар аудару қажет. (*) өрнегінен: бірқалыпты және бірқалыпты түзу сызықтық қозғалыс кезінде санақ жүйелерінің бір-біріне қатысты үдеулері тең болады, яғни
Дененің әр түрлі санақ жүйелеріндегі үдеулеріне назар аудару қажет. (*) өрнегінен: бірқалыпты және бірқалыпты түзу сызықтық қозғалыс кезінде санақ жүйелерінің бір-біріне қатысты үдеулері тең болады, яғни
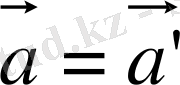 . Шынында да, егер
. Шынында да, егер
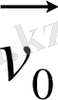 - модулі және бағыты уақыт өзгергенде тұрақты қалатын вектор болса, онда дененің салыстырмалы жылдамдығының
- модулі және бағыты уақыт өзгергенде тұрақты қалатын вектор болса, онда дененің салыстырмалы жылдамдығының
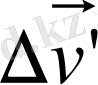 кез келген өзгерісі оның
кез келген өзгерісі оның
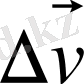 абсолют жылдамдығының өзгерісімен сәйкес келеді. Соның салдарынан:
абсолют жылдамдығының өзгерісімен сәйкес келеді. Соның салдарынан:
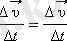
 ұмтылғандағы шекке көшкенде,
ұмтылғандағы шекке көшкенде,
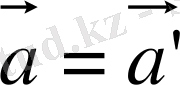 аламыз. Жалпы жағдайда санақ жүйелерінің бір-біріне қатысты үдеумен қозғалысы кезінде дененің үдеуі әрбір санақ жүйелерінде әр түрлі болады. Салыстырмалы қозғалыстың векторы
аламыз. Жалпы жағдайда санақ жүйелерінің бір-біріне қатысты үдеумен қозғалысы кезінде дененің үдеуі әрбір санақ жүйелерінде әр түрлі болады. Салыстырмалы қозғалыстың векторы
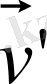 және тасымал жылдамдықтың
және тасымал жылдамдықтың
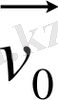 векторлары бір-біріне параллель болған жағдайда, жылдамдықтарды қосу заңы скаляр түрде жазуға болады:
векторлары бір-біріне параллель болған жағдайда, жылдамдықтарды қосу заңы скаляр түрде жазуға болады:
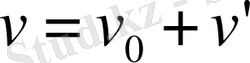 .
.
Бұл жағдайда барлық қозғалыстар бір түзу сызықтың (мысалы, ОХ осінің) бойымен болады.
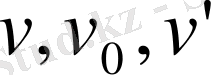 жылдамдықтарын абсолют, тасымал және салыстырмалы жылдамдықтарының ОХ осіне проекциялары ретінде қарастыру қажет. Олар алгебралық шамалар болып табылады және соның салдарынан, оларға қозғалыстың бағытына сәйкес «+» немесе «-» таңбасын қою қажет.
жылдамдықтарын абсолют, тасымал және салыстырмалы жылдамдықтарының ОХ осіне проекциялары ретінде қарастыру қажет. Олар алгебралық шамалар болып табылады және соның салдарынан, оларға қозғалыстың бағытына сәйкес «+» немесе «-» таңбасын қою қажет.
- Бірқалыпты қозғалыс
Механикалық қозғалыстың қарапайым қозғалысына түзу сызықтың бойымен модулі және бағыты бойынша тұрақты қозғалысы жатады. Мұндай қозғалысты бірқалыпты деп атайды. Бірқалыпты қозғалыс кезінде дене бірдей уақыт аралықтары ішінде бірдей жол жүреді. Бірқалыпты түзу сызықты қозғалысты сипаттау үшін, ОХ координаталық осін қозғалыс сызығының бойымен орналастыру ыңғайлы. Бірқалыпты қозғалыс кезінде дененің орны бір х координатасының беруімен анықталады. Орын ауыстыру және жылдамдық векторлары әрқашан ОХ координаттық осіне параллель орналасады. Сондықтан бірқалыпты түзу сызықтық қозғалыс кезінде орын ауыстыру және жылдамдық векторларын ОХ осіне проекциялап, олардың проекцияларын алгебралық шамалар ретінде қарастыруға болады. Егер қандай да бір t 1 уақытта дене координатасы х 1 -ге тең нүктеде орналасқан болып, ал кейінгі t 2 кезінде координатасы х 2 -ге тең нүктеде орналасқан болса, онда Δs орын ауыстыруының Δt = t 2 -t 1 уақыт ішіндегі ОХ осіне проекциясы Δ s = x 2 - x 1
тең болады. Бұл шама дене қозғалып келе жатқан бағытына байланысты оң да, теріс те болуы мүмкін. Түзу бойымен бірқалыпты қозғалған кезде орын ауыстырудың модулі жүрілген жолға тең болады.
Бірқалыпты түзу сызықты қозғалыстың жылдамдығы деп
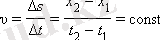 қатынасын айтады. Егер
v
> 0 онда дене ОХ осінің оң бағытына қарай қозғалады, егер
v
< 0, онда қарама-қарсы бағытта қозғалады. х координатасының t уақыттан тәуелділігі (
қозғалыс заңы
) бірқалыпты түзусызықты қозғалыста
сызықты математикалық теңдеумен
өрнектеледі:
x
(
t
) =
x
0
+ v
t
.
қатынасын айтады. Егер
v
> 0 онда дене ОХ осінің оң бағытына қарай қозғалады, егер
v
< 0, онда қарама-қарсы бағытта қозғалады. х координатасының t уақыттан тәуелділігі (
қозғалыс заңы
) бірқалыпты түзусызықты қозғалыста
сызықты математикалық теңдеумен
өрнектеледі:
x
(
t
) =
x
0
+ v
t
.
Бұл теңдеуде v = const - дене қозғалысының жылдамдығы, x 0 - дененің t = 0 кезіндегі нүктенің координатасы. Графикте x ( t ) қозғалыс теңдеуі түзу сызықпен көрсетіледі. Мұндай графиктердің мысалдары 1. 3. 1. -суретте көрсетілген.
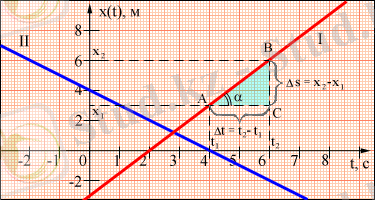 1. 3. 1. -сурет. Бірқалыпты түзусызықты қозғалыстың графиктері.
1. 3. 1. -сурет. Бірқалыпты түзусызықты қозғалыстың графиктері.
1. 3. 1-суретте I-графиктегі қозғалыс заңы үшін t = 0 кезінде дене координатасы x 0 = -3 нүктесінде орналасқан. t 1 = 4 с және t 2 = 6 с уақыттарының арасында дене x 1 = 3 м нүктесінен x 2 = 6 м нүктесіне орын ауыстырды. Сонымен, Δ t = t 2 - t 1 = 2 с уақыт ішінде дене Δ s = x 2 - x 1 = 3 м шамаға орын ауыстырды. Сондықтан, дененің жылдамдығы
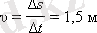 тең болады.
тең болады.
Жылдамдықтың шамасы оң болып шықты. Бұл дене ОХ осінің оң бағытының бойымен қозғалғанын көрсетеді. Графикте дененің жылдамдығын геометриялық түрде, яғни ВС және АС қабырғаларының қатынасы түрінде анықтауға болатынына назар аударыңыз (1. 3. 1. суретін қараңыз) :
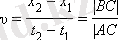
Түзу мен уақыт осінің арасындағы α бұрышы неғұрлым үлкен болса, яғни графиктің бұрылуы неғұрлым көп болса, соғұрлым дененің жылдамдығы да көп болады. Кейде дененің жылдамдығы x ( t ) түзуінің α бұрылу бұрышының тангенсіне тең болады деп атайды. Математикада бұл тұжырым әр кезде дұрыс бола бермейді, өйткені АВС теңдеуінің ВС және АС қабырғаларының өлшемдері әр түрлі: ВС қабырғасы метрмен, ал АС қабырғасы - секундпен өлшенеді.
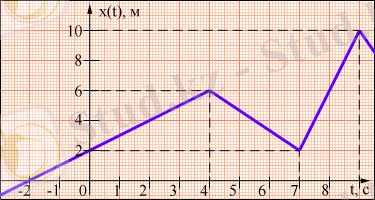
Дәл осылай 1. 3. 1-суреттегі II түзуінің қозғалысы үшін x 0 = 4 м, υ = -1 м/с табамыз. 1. 3. 2. -суретте x ( t ) қозғалыс заңы түзу сызықтардың кесінділерінің көмегімен көрсетіледі. Математикада мұндай графиктерді бөлік-сызық графиктер деп атайды. Түзудің бойымен мұндай қозғалыс бірқалыпты болып табылмайды . Графиктің әр түрлі бөліктерінде дене әр түрлі жылдамдықтармен қозғалады, оларды сәйкес кесіндінің уақыт осіне қатысты бұрылуы бойынша анықтауға болады. График сынған нүктелерде дене өз жылдамдығын лезде өзгертеді. Графикте (1. 3. 2. сурет) бұл t 1 = -3 с, t 2 = 4 с, t 3 = 7 с и t 4 = 9 с кезінде болады. ( t 2 ; t 1 ) интервалында дене υ 12 = 1 м/с жылдамдығымен, ( t 3 ; t 2 ) интервалында - υ 23 = -4/3 м/с жылдамдығымен, ( t 4 ; t 3 ) интервалында υ 34 = 4 м/с жылдамдығымен қозғалатынын табу қиын емес. Бөлік-сызық қозғалыс кезінде дененің жүрген жолы l орын ауыстырумен s сәйкес келмейді.
1. 3. 2. -сурет. Бөлік-сызық қозғалыс заңы.
Мысалы 1. 3. 2. -суретте көрсетілген қозғалыс заңы үшін уақыттың 0-ден 7-ге дейінгі интервалында дененің орын ауыстыруы 0-ге тең ( s = 0) . Осы уақыт ішінде дене l = 8 м жол жүрді.
1. 4. Бірқалыпты үдемелі қозғалыс
Жалпы жағдайда
бірқалыпты үдемелі қозғалыс
деп үдеу векторы
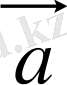 модулі және бағыты жағынан тұрақты болатын қозғалысты айтады. Мұндай қозғалыстың мысалы ретінде горизонтпен белгілі бұрышпен лақтырылған тастың қозғалысы бола алады (ауаның кедергісі ескерілмейді) . Траекторияның кез келген нүктесінде тастың үдеуі еркін құлау үдеуіне тең
модулі және бағыты жағынан тұрақты болатын қозғалысты айтады. Мұндай қозғалыстың мысалы ретінде горизонтпен белгілі бұрышпен лақтырылған тастың қозғалысы бола алады (ауаның кедергісі ескерілмейді) . Траекторияның кез келген нүктесінде тастың үдеуі еркін құлау үдеуіне тең
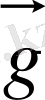 болады. Тас қозғалысының кинематикалық сипаттамасын беру үшін, координаттар жүйесін осьтердің біреуі (мысалы OY) үдеу векторына параллель бағыттайды. Онда тастың қисық сызықты қозғалысын екі қозғалыстардың - OY осінің бойымен түзусызықты
бірқалыпты үдемелі қозғалыстың
және перпендикуляр бағыттағы (яғни OX осінің бойымен)
бірқалыпты түзу сызықты қозғалыстардың
қосындысы түрінде беруге болады (1. 4. 1-сурет) .
болады. Тас қозғалысының кинематикалық сипаттамасын беру үшін, координаттар жүйесін осьтердің біреуі (мысалы OY) үдеу векторына параллель бағыттайды. Онда тастың қисық сызықты қозғалысын екі қозғалыстардың - OY осінің бойымен түзусызықты
бірқалыпты үдемелі қозғалыстың
және перпендикуляр бағыттағы (яғни OX осінің бойымен)
бірқалыпты түзу сызықты қозғалыстардың
қосындысы түрінде беруге болады (1. 4. 1-сурет) .
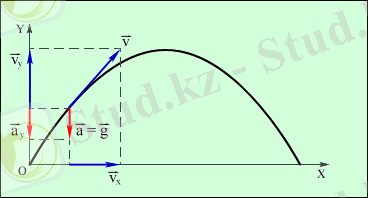 1. 4. 1. -сурет.
1. 4. 1. -сурет.
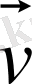 жылдамдықтың және
жылдамдықтың және
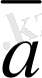 үдеу векторларының координат осьтеріне проекциялары.
үдеу векторларының координат осьтеріне проекциялары.
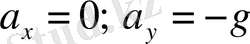 .
.
Сонымен, бірқалыпты үдемелі қозғалысты зерттеу түзу сызықты бірқалыпты үдемелі қозғалысты зерттеуге келтіріледі. Түзу сызықты қозғалыс жағдайында жылдамдық
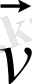 және үдеу
және үдеу
 векторлары қозғалыс түзуінің бойымен бағытталады. Сондықтан
векторлары қозғалыс түзуінің бойымен бағытталады. Сондықтан
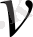 жылдамдығын және
жылдамдығын және
 үдеуін қозғалыс бағытына проекциялап, алгебралық шамалар ретінде қарастыруға болады.
үдеуін қозғалыс бағытына проекциялап, алгебралық шамалар ретінде қарастыруға болады.
Бірқалыпты үдемелі қозғалыс кезінде дененің жылдамдығы
(*) формуласымен анықталады.
Бұл формуладағы υ 0 t = 0 болғандағы дененің жылдамдығы. a = const - үдеу. Графикте υ( t ) тәуелділігі түзу сызығымен бейнеленген (1. 4. 2-сурет) .
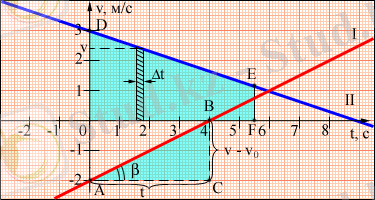 1. 4. 2. -сурет. Бірқалыпты үдемелі қозғалыс жылдамдығының графигі a үдеуі жылдамдық графигінің көлбеуі арқылы анықталуы мүмкін. 1. 4. 2. -суретіндегі сәйкес салулар І-графигіне арналған. Үдеудің сандық мәні АВС үшбұрышының қабырғаларының қатынасына тең болады:
1. 4. 2. -сурет. Бірқалыпты үдемелі қозғалыс жылдамдығының графигі a үдеуі жылдамдық графигінің көлбеуі арқылы анықталуы мүмкін. 1. 4. 2. -суретіндегі сәйкес салулар І-графигіне арналған. Үдеудің сандық мәні АВС үшбұрышының қабырғаларының қатынасына тең болады:
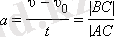
Жылдамдық графигі мен уақыт осінің арасындағы β бұрышы неғұрлым үлкен болса, яғни графиктің көлбеулігі неғұрлым үлкен болса, дененің үдеуі соғұрлым үлкен болады.
І графигі үшін: υ 0 = -2 м/с, a = 1/2 м/с 2 .
ІІ графигі үшін: υ 0 = 3 м/с, a = -1/3 м/с 2 .
Жылдамдық графигі қандай да бір t уақыт аралығында дененің s орын ауыстыруының проекциясын анықтауға мүмкіндік береді. Уақыт осінен қандай да бір Δ t уақыт аралығын бөліп алайық. Егер бұл аралық жеткілікті кіші болса, онда осы аралықта жылдамдықтың өзгеру аралығы үлкен болмайды, яғни осы уақыт аралығындағы Δ t уақыт аралығындағы v лездік жылдамдыққа тең орташа бірқалыпты жылдамдық деп санауға болады. Соның салдарынан, Δ t уақыт аралығындағы Δ s орын ауыстыруы Δ s = υΔ t тең болады. Бұл орын ауыстыру 1. 4. 2. -суретте көрсетілген штрихталған ауданға тең. 0-ден қандай да бір t моментіне дейінгі уақытты Δ t кіші аралықтарына бөлсе, дененің бірілген t уақыт ішіндегі s орын ауыстыруы бірқалыпты түзу сызықты қозғалысы ODEF трапециясының ауданын алуға болады. Сәйкес салулар ІІ- график үшін 1. 4. 2. суретінде орындалған. t уақыты 5, 5 с.
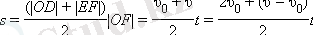
υ - υ 0 = at тең болғандықтан, 0-ден t уақыт аралығындағы бірқалыпты үдемелі қозғалыс кезіндегі дененің s орын ауыстыруы келесі қорытқы формула арқылы жазылады:
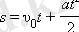
 (**)
(**)
Дененің кез келген t уақыт моментіндегі y координатасын табу үшін, бастапқы
y
0
координатасына t уақыт кезіндегі орын ауыстыруын қосады.
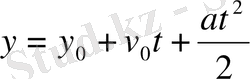
(***)
Бұл өрнек бірқалыпты үдемелі қозғалыстың заңы деп атайды.
Бірқалыпты үдемелі қозғалысты талдау кезінде берілген бастапқы υ 0 , соңғы υ және a үдеуінің мәндері арқылы дененің орын ауыстыруын табу есебі қойылады. Бұл есеп (*), (**) теңдеулерінен t уақытты шығарып тастау арқылы шешіледі. Нәтиже
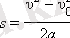 түрінде жазылады.
түрінде жазылады.
Осы формуладан s орын ауыстыруы, a үдеуі және v 0 бастапқы жылдамдығы белгілі болса, соңғы v жылдамдығы келесі формула арқылы табылады:
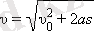 Егер υ
0
=0 болса, онда осы формулалар
Егер υ
0
=0 болса, онда осы формулалар
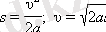 түріне келеді.
түріне келеді.
Бірқалыпты түзу сызықты үдемелі қозғалыстың формулаларына кіретін υ 0 , υ, s , a , y 0 шамалары алгебралық шамалар болып табылады. Нақтылы жағдайда бұл шамалар оң да, теріс те болуы мүмкін.
1. 5. Денелердің еркін түсуі
Денелердің еркін түсуі деп ауа кедергісі болмағандағы денелердің Жерге түсуін айтады. XVI ғасырдың аяғында ұлы итальян Г. Галилей тәжірибелік жолмен сол заманға сай уақыт дәлдігімен ауа болмағанда барлық денелер Жерге бірқалыпты үдемелі түсетінін және барлық денелердің үдеулері бірдей болатынын анықтады. Осыдан 2000 жыл бұрын Аристотельден бастап ғылымда ауыр денелер жеңіл денелерге қарағанда Жерге жылдамырақ түсетіні ұйғарылды.
Денелердің Жерге түсетін үдеуді
еркін түсу үдеуі
деп аталады. Еркін түсу үдеуінің векторы
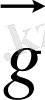 символымен белгіленеді, оның бағыты вертикаль төмен бағытталады. Жер шарының әр түрлі нүктелерінде географиялық ені және бойына, теңіз деңгейіне байланысты
g-
дің сандық мәні бірдей болмайды. Жуық шамамен
полюстерде
9, 83 м/с
2
-ден
экваторда
9, 78 м/с
2
дейін өзгереді.
Мәскеудің
енінде
g
= 9, 81523 м/с
2
. Әдетте есептеулерде жоғары дәлдік қажет болмаса, онда Жер бетіндегі
g
-дің сандық мәні ретінде 9, 8 м/с
2
немесе тіпті 10 м/с
2
деп алады.
символымен белгіленеді, оның бағыты вертикаль төмен бағытталады. Жер шарының әр түрлі нүктелерінде географиялық ені және бойына, теңіз деңгейіне байланысты
g-
дің сандық мәні бірдей болмайды. Жуық шамамен
полюстерде
9, 83 м/с
2
-ден
экваторда
9, 78 м/с
2
дейін өзгереді.
Мәскеудің
енінде
g
= 9, 81523 м/с
2
. Әдетте есептеулерде жоғары дәлдік қажет болмаса, онда Жер бетіндегі
g
-дің сандық мәні ретінде 9, 8 м/с
2
немесе тіпті 10 м/с
2
деп алады.
Еркін түсу үдеуінің мысалы болып бастапқы жылдамдығы 0-ге тең
h
биіктігінен құлаған дене болып табылады. Еркін түсу - түзу сызықты үдеуі тұрақты қозғалыс болып табылады. Егер бастапқы координатасын Жердің бетімен беттестіріп, OY координаттық осін вертикаль жоғары бағыттасақ, онда бастапқы жылдамдықсыз еркін түсуді талдау үшін
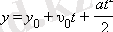 формуласын қолданады, мұндағы υ
0
= 0,
y
0
=
h
,
a
= -
g
. Егер дене құлаған кездегі координатасы
y
<
h
нүктеде болса, дененің
s
орын ауыстыруы
s
=
y
-
h
< 0 болатынына назар аударыңыз. Бұл шама теріс, өйткені дене құлаған кезде OY осі бойынша оң шамаға қарама-қарсы бағытталады. Нәтижесінде: υ = -
gt
. аламыз. Жылдамдық векторы төмен бағытталғандықтан, жылдамдық теріс.
формуласын қолданады, мұндағы υ
0
= 0,
y
0
=
h
,
a
= -
g
. Егер дене құлаған кездегі координатасы
y
<
h
нүктеде болса, дененің
s
орын ауыстыруы
s
=
y
-
h
< 0 болатынына назар аударыңыз. Бұл шама теріс, өйткені дене құлаған кезде OY осі бойынша оң шамаға қарама-қарсы бағытталады. Нәтижесінде: υ = -
gt
. аламыз. Жылдамдық векторы төмен бағытталғандықтан, жылдамдық теріс.
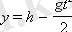
Жерге құлау уақыты
t
n
y
= 0 шартынан анықталады.
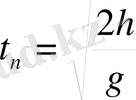
Дененің кез келген нүктесіндегі жылдамдығы:
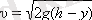
Дербес жағдайда
y
= 0 болғанда υ
n
Жерге түсу жылдамдығы:
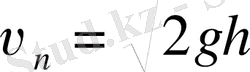
Осы формулаларды қолданып, берілген биіктіктен түсу уақытын, құлап бастағаннан кейінгі кез келген моменттегі және траекторияның кез келген нүктесіндегі дененің жылдамдығын есептеуге болады.
Дәл осылайша бастапқы жылдамдығы υ
0
вертикаль жоғары лақтырылған дененің қозғалысы анықталады. Егер OY осін бұрынғыша вертикаль жоғары бағыттаса, ал оның басын лақтыру нүктесімен беттестірсе, онда бірқалыпты түзу сызықты үдемелі қозғалыстың формулаларында
y
0
= 0, υ
0
> 0,
a
= -
g
деп алады. Бұл υ = υ
0
-
gt
. береді. υ
0
/
g
уақыттан кейін υ дененің жылдамдығы 0-ге айналады, яғни дене ең жоғары көтерілу нүктесіне жетеді. y координатасының t уақыттан тәуелділігі
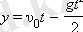 формуласы бойынша анықталады.
формуласы бойынша анықталады.
Дене Жерге ( y = 0) 2υ 0 / g уақыттан кейін түседі, соның салдарынан көтерілу және құлау уақыттары бірдей. Жерге құлау кезіндегі дененің жылдамдығы -υ 0 -ға тең, яғни дене жоғары лақтырылған жылдамдықтың модулімен бірдей жылдамдықпен жерге құлайды.
Максималды көтерілу биіктіігі:
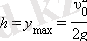
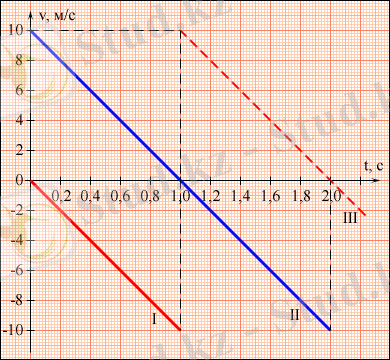
1. 5. 1. -сурет. Дененің a = - g үдеумен әр түрлі қозғалыс режіміндегі жылдамдықтар графиктері
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz