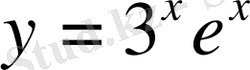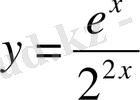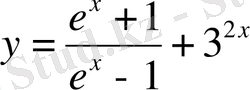Көрсеткіштік функция: қасиеттері, графигі және мектепте көрсеткіштік теңдеулер мен теңсіздіктерді оқыту әдістемесі


СОДЕРЖАНИЕ
КІРІСПЕ3
Негізгі бөлім5
Көрсеткіштік функция6
Көрсеткіштік функцияның графигі7
Қарапайым көрсеткіштік теңдеу. 10
Көрсеткіштік теңдеулерді шешу10
Көрсеткіштік теңдеулер жүйесін шешу11
Көрсеткіштік теңсіздіктер12
Қортынды. 26
ӘДЕБИЕТТЕР ТІЗІМІ. 27
КІРІСПЕ
Қазақстан Республикасының Білім туралы заңында білім беру саласындағы мемлекеттің, басты принциптері ретінде жеке адамның білімділігін ынталандыру және дарындылығын дамыту, білім берудің дамытушы сипатын арттыру, білім беру жүйесің ақпараттындыру мәселелері айқындалды. Осы мәселелер Еліміз Президенті Н. Ә. Назарбаевтың Қазақстан 2030 атты Қазақстан Халқына жолдауында басым міндеттер қатарына қойылған.
Еліміздіің соңғы 10 жыл ішінде қоғамда демократияландыру және ізгілендіру саласында жүргізілген біршама реформалар, экономикалық өзгерістер жалпы орта білім беретін мектептегі оқу процесін, оқушының қабілеті мен қызығушылығына сәйкес дербестіндіру қажеттілігін алға қойып отыр.
Қазіргі информациялау дәуірінде математиканың негізін меңгеру жасұрпаққа білім беру мен тәрбиелеудің бірден-бір негізгі элементі болып табылады. Кәзіргі кезде дүние жүзіндегі көптеген елдерде математикадан мектептерде жүйелі де, сапалы білім беруге аса назар аударылып отырғаны белгілі. Бұл жөніндегі дүние жүзілік тәжірибеге талдау жасайтын болсақ, онда мынандай үш тенденцияны байқауға болады: барлық оқушыларға математикадан белгілі-бір дәрежеде білім берудің қажеттілігі және оған сәйкес ғылыми-зерттеу жұмыстарды кеңінен жүргізу. Математиканы негізгі курс ретінде жалпы білім беретін мектептердің сатысының оқу жоспарына енгізу: мектептің жоғарғы сатысында математикадан білім беруді жеке даралау мен топтау әдістері арқылы іске асыруды кеңінен енгізу.
Математика оқушыларды индукция және дедукциямен, жалпылау мен нақтылаумен, анализ бен синтезбен, жіктеу және жүйеге келтірумен, абстракциялаумен аналогиямен таныстыра отырып, олардың ой өрісін едәуір кеңейтеді.
Математика курсының міндеті -оқушылардың логикалық ойлауын дамыту. Логикалық интуицияны дамытып, осының нәтижесінде математика мектеп оқушыларының ғылыми-техникалық ойлауын қалыптастыруда жетекші орын алады.
Математика оқытудың мақсаты-жеке тұлғаны қоғамның даму барысында алатын оның орнына лайық функциялды сауаттылығын қалыптастыруға байланысты анықталады. Математиканы кәсіби меңгеруге даярлаумен қатар таңдапалған мамандықтарына тәуелсіз барлық оқушыларға математикалық даярлықтың кепілді деңгейін қамтамасыз ету.
Математиканы оқытудың білімділік мақсаты-барлық оқушыларды математика ғылымның негізі болатын білімдер жүйесі мен және ол білімдерді сапалы түрде қолдана алудың іскерліктері мен дағдыларын берік қалыптастыру болып табылады. Аталған білім, білік, дағдыны қалыптастыру математикалық жекелеген тараулары арқылы жүзеге асырылады. Сол тараулардың бірі-көрсеткіштік функция.
Зертеу нысаны алгебра курстында көрсеткіштік функция тақырыбын оқытудың әдістемесі. Тарауды оқу барысында оқушылардың білім-білік дағдысына қойылатын талаптар:
- Көрсеткіштік функцияның қасиеттерін меңгеру және графигін сала алу.
- Көрсеткіштік теңдеулерді шешу әдістерін меңгеру.
- Көрсеткіштік теңсіздіктер шешу әдістерін меңгеру.
- Көрсеткіштік таңдеулерді шешу әдістерін меңгеру.
- Туындыны және алғашқы функцияны табуда математикалық анализдің негізгі аппараттарын қолдана алу. (туынды мен алғашқы функциясын табу формулаларын қолдану)
Негізгі бөлім
Мектеп курсында көрсеткіштік және логарифмдік функцияға (36 сағат) бөлінген. (2003ж оқу бағдарламасы бойынша ) математика жаратылыс тану бағытындағы сыныптарға (18 сағат) берілген, яғни көрсеткіштік функцияға, теңдеуге, теңсіздіктерді (18 сағатта) көлемінде қарастырылады.
Қарастырылатын тақырыптар:
- Көрсеткіштік функция, қасиеттері және графигі.
- Көрсеткіштік теңдеу.
- Көрсеткіштік теңсіздік.
- Көрсеткіштік теңдеулер жүйесі және теңсіздік.
Негізгі мақсат -оқушыларды көрстекіштік функциямен таныстыру. Анықталу облысы, мәндер жиыны, графигін салуды меңгерту. Көрсеткіштік теңдеулерді, теңсіздіктерді шешу әдістерін меңгерту, бөгде түбірлерді зерттеу.
Көрсеткіштік функция
Егер а>0, а
 1 болса, онда у=а
х
функциясын негізі а-ға тең көрсеткіштік функция деп атайды. Мысалы, у=3
х
; у=10
х
; у=0, 2
х
; у=
1 болса, онда у=а
х
функциясын негізі а-ға тең көрсеткіштік функция деп атайды. Мысалы, у=3
х
; у=10
х
; у=0, 2
х
; у=
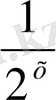 ; у=(
; у=(
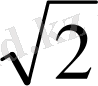 )
)
 және т. с. с. көрсеткіштік функциялар болады. Анықтамадағы а>0, а
және т. с. с. көрсеткіштік функциялар болады. Анықтамадағы а>0, а
 1 шарттары өте маңызды. Мәселен, нақты көрсеткіштік дәрежелер тек оң сандар үшін анықталғандықтан, а>0 болуы қажет. Екінші жағынан, егер а=1 болса, онда әрбір х
1 шарттары өте маңызды. Мәселен, нақты көрсеткіштік дәрежелер тек оң сандар үшін анықталғандықтан, а>0 болуы қажет. Екінші жағынан, егер а=1 болса, онда әрбір х
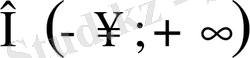 мәндерінде у=а
х
=1
х
=1 болып, функция х-ке тәуелді болмай қалады (бұл жағдайда кейде функцияны тұрақты функция у=1 ретінде қарастырылады)
мәндерінде у=а
х
=1
х
=1 болып, функция х-ке тәуелді болмай қалады (бұл жағдайда кейде функцияны тұрақты функция у=1 ретінде қарастырылады)
Сонымен, енді көрсеткіштік у=а
х
функциясы а>0 және а
 1 болғанда анықталған деп есептейміз. Көрсеткіштік функцияның мынандай қасиеттері бар:
1 болғанда анықталған деп есептейміз. Көрсеткіштік функцияның мынандай қасиеттері бар:
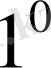 Көрсеткіштік функцияның анықталу облысы
Көрсеткіштік функцияның анықталу облысы
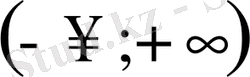 жиыны болады.
жиыны болады.
2

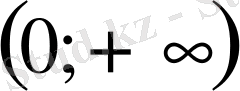 жиыны көрсеткіштік функцияның мәндерінің облысы болады, яғни 0, х
жиыны көрсеткіштік функцияның мәндерінің облысы болады, яғни 0, х
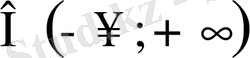 теңсіздігі орындалады .
теңсіздігі орындалады .
3
 . а) Егер а>0 және х>0 болса, онда а
х
>1 болады;
. а) Егер а>0 және х>0 болса, онда а
х
>1 болады;
ә) егер а>1 және х<0 болса, онда а х < 1 болады;
б) егер а< 1 және х>0 болса, онда а х < 1 болады;
в) егер а< 1 және х<0 болса, онда а х >1 болады;
г) егер а>0 х=0 болса, онда а
 =1 болады.
=1 болады.
4
 . Егер а>1 болса, онда көрсеткіштік у=а
х
функциясы өспелі болады, яғни х
. Егер а>1 болса, онда көрсеткіштік у=а
х
функциясы өспелі болады, яғни х
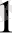 < х
< х
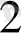 теңсіздігін қанағаттандыратын әрбір х
теңсіздігін қанағаттандыратын әрбір х
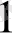 , х
, х
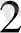 нақты сандары үшін а
нақты сандары үшін а
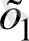 < а
< а
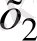 теңсіздігі орындалады.
теңсіздігі орындалады.
5
 Егер 0< а < 1 болса, онда у=а
х
көрсеткіштік функциясы кемімелі
Егер 0< а < 1 болса, онда у=а
х
көрсеткіштік функциясы кемімелі
болады, яғни х
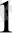 < х
< х
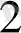 теңсіздігін қанағаттандыратын әрбір х
теңсіздігін қанағаттандыратын әрбір х
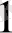 , х
, х
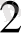 нақты сандары үшін а
нақты сандары үшін а
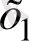 >а
>а
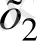 теңсіздігі орындалады.
теңсіздігі орындалады.
Дәлелдеу .
1. Бұл қасиеттің дәлелдеуі анықтамадан шығады. .
2. Оң санның рационал қөрсеткішті дәрежесі оң сан болатынын білеміз, яғни х рационал сан болғанда а
х
>0 теңсіздігі орындалады. Онда а
х
>0 теңсіздігі кез келген иррационал х үшін орындалады (
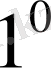 -қасиет) .
-қасиет) .
3. а) Егер а>1 және х>0 болса, онда нақты қөрсеткішті дәреженің 2
 қасиеті бойынша а
х
>1
х
=1
қасиеті бойынша а
х
>1
х
=1
ә) Егер а>1 және х<0 болса, онда а х < 1 х =1 б) және в) пункттері де осы сияқты дәләлденеді . Ал г) пунктінің дәлелдеуі көрсеткіші о-ге тең дәреже анықтамасынан шығады.
4. a>1 және х 1 < х 2 болсын. Онда
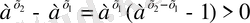 ,
,
себебі, х
2
-х
1
>0 болғандықтан,
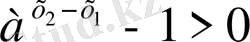 . Олай болса, теңсіздіктің анықтамасы бойынша
. Олай болса, теңсіздіктің анықтамасы бойынша

- 0<a<1 және х1< х2болсын. Онда
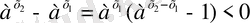 ,
,
себебі
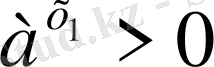 , ал х
2
-х
1
>0 және 0<a<1 болғандықтан
, ал х
2
-х
1
>0 және 0<a<1 болғандықтан
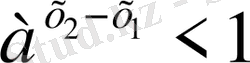 . Қасиеттер толық дәлелденді.
. Қасиеттер толық дәлелденді.
Көрсеткіштік функцияның графигі
Алдымен кестелер көмегімен у=2
х
және у=
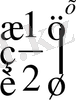 функцияларының графиктерін салып көрейік:
функцияларының графиктерін салып көрейік:

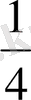
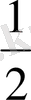
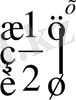
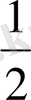
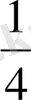

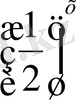 Табылған нүктелерді координаталық жазықтықта бейнелеп, оларды біркелкі тегіс сызықтармен қосамыз. Сонда у=2
х
және у=
Табылған нүктелерді координаталық жазықтықта бейнелеп, оларды біркелкі тегіс сызықтармен қосамыз. Сонда у=2
х
және у=
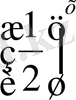 функцияларының графиктерін аламыз.
функцияларының графиктерін аламыз.
Дәреженің қасиеті бойынша 1<a<b жағдайында, егер х>0 болса, онда а х <b x теңсіздігі; егер х<0 болса, онда а х >b x теңсіздігі орындалады. Ал, керісінше 0<a<b<1 жағдайында, егер х>0 болса, онда а х >b x теңсіздігі; егер х<0 болса, онда а х <b x теңсіздігі орындалады. Олай болса, негізі а 1 ден неғұрлым үлкен болса, онда сәйкес у=a x көрсеткіштік функциясы соғұрлым «жылдамырақ өседі. Ал, негізі а 1 ден неғұрлым кіші болған сайын сәйкес у=a x көрсеткіштік функциясы соғұрлым жылдамырақ кемиді. Мысалы төмендегі суретте көрсеткіштік функцияның негізі а=0, 8; а=0, 4; а=3; а=2 болғандағы сәйкес көрсеткіштік функциялар графиктері салынған.
Қарапайым көрсеткіштік теңдеу.
Егер а>1, а
 1 және b >0 болса, онда
1 және b >0 болса, онда
а х =b (1)
теңдеуін қарапайым көрсеткіштік теңдеу деп атайды, егер b>0 болса, онда бір түбірі бар екенін, ал b
 0 болғанда оның түбірлері болмайтынын көрсеткенбіз. Осы мәліметтер бойынша b>0 жағдайында (1) теңдеудің жалғыз түбірі
0 болғанда оның түбірлері болмайтынын көрсеткенбіз. Осы мәліметтер бойынша b>0 жағдайында (1) теңдеудің жалғыз түбірі
х=log
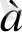 b (2)
b (2)
теңдігімен анықталатындығы шығады.
1-мысал. 2 х-2 =16 теңдеуін шешейік.
Шешуі.
(2) формула бойынша
х-2=log 2 16⇔ х=2+log 2 2 4 ⇔ х=2+4log 2 2⇔x=6 болады.
Жауабы: х=6
Көрсеткіштік теңдеулерді шешу
Әдетте көрсеткіштік теңдеулерді
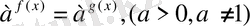 (3)
(3)
түріне келтіріп шешеді. Бұл теңдеу у=f(x) және y=g(x) функцияларының ортақ анықталу облысында f(x) =g(x) теңдеуімен мәндес болады.
2-мысал. 81 х -2⋅9 х -3=0 теңдеуін шешейік.
Шешуі.
Мұнда 9 х =у белгілеуін енгізсек, онда берілген теңдеуді у 2 -2у-3=0 түрінде жазамыз. Осыдан у 1 =-1, у 2 =3. 9 х өрнегі тек оң мәндер қабылдағандықтан у 1 =-1 түбірін қарастырмаймыз, онда 9 х =3 теңдеуінен х=0, 5 теңдігін аламыз. Жауабы. 0, 5.
3-мысал. 6·9 х -13⋅6 х +6⋅4 х =0 теңдеуін шешейік.
Шешуі.
Теңдеуді 6·3
2х
-13⋅2
х
⋅3
х
+6⋅2
2х
=0 түрінде жазып, оны 2
2х
(2
2х
 0 ) өрнегіне бөлеміз: 6·
0 ) өрнегіне бөлеміз: 6·
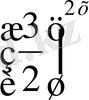 -13⋅
-13⋅
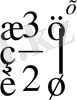 +6 =0. Мұнда
+6 =0. Мұнда
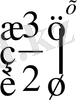 =у белгілеуін енгізсек, онда берілген теңдеуді 6у
2
-13у+6=0 теңдеуімен алмастырамыз. Бұл теңдеудің түбірлері у
1
=
=у белгілеуін енгізсек, онда берілген теңдеуді 6у
2
-13у+6=0 теңдеуімен алмастырамыз. Бұл теңдеудің түбірлері у
1
=
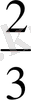 , у
2
=
, у
2
=
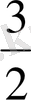 . Онда
. Онда
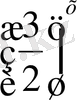 =
=
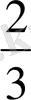 және
және
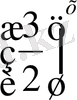 =
=
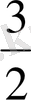 теңдеулер берілген есептің жауабын аламыз: х
1
=-1 және : х
2
=1.
теңдеулер берілген есептің жауабын аламыз: х
1
=-1 және : х
2
=1.
4- мысал. х
2
⋅
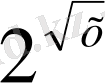 +х+2=
+х+2=
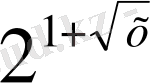 + х
2
+х⋅
+ х
2
+х⋅
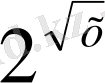 теңдеуін шешейік.
теңдеуін шешейік.
Теңдеудің мүмкін мәндер жиыны х
 0 теңсіздігімен анықталады. Топтау арқылы берілген теңдеуді х
2
⋅(
0 теңсіздігімен анықталады. Топтау арқылы берілген теңдеуді х
2
⋅(
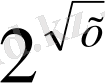 -1) -х(
-1) -х(
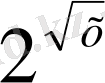 -1) -2(
-1) -2(
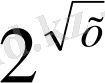 -1) =0 не (х
2
-х-2) (
-1) =0 не (х
2
-х-2) (
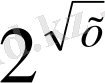 -1) =0 түріне келтіреміз. Онда берілген теңдеу х
2
-х-2=0 және (
-1) =0 түріне келтіреміз. Онда берілген теңдеу х
2
-х-2=0 және (
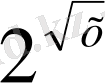 -1) =0 теңдеулері жиынтығымен тең шамалы. Бірінші теңдеудің түбірлері х
1
=-1 және х
2
=2 болса, екінші теңдеудің шешімі х
3
=0. Мұнда -1
-1) =0 теңдеулері жиынтығымен тең шамалы. Бірінші теңдеудің түбірлері х
1
=-1 және х
2
=2 болса, екінші теңдеудің шешімі х
3
=0. Мұнда -1
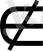 [0; +∞) және 0; 2
[0; +∞) және 0; 2
 [0; +∞) болғандықтан есептің жауабы: 0; 2.
[0; +∞) болғандықтан есептің жауабы: 0; 2.
Сонымен қатар
[a(x) ] f(x) = [a(x) ] g(x) (4)
түріндегі көрсеткіштік-дәрежелік теңдеулер де кездеседі. Мұнда f(x) және g(x) өрнектерінің анықталу облыстары мен а(х) >0 теңсіздігін қанағаттандыратын х айнымалысының мәндері жиындарының қиылысуы теңдеудің ММЖ (мүмкін мәндер жиыны ) ын анықтайды. Егер m>0, m
 Equation. 3 1 болса, онда (4) теңдеу
Equation. 3 1 болса, онда (4) теңдеу
f(x) log m a(x) = g(x) log m a(x)
теңдеуімен мәндес. Ал бұл теңдеу мынандай екі теңдеумен мәндес:
log m a(x) =0, f(x) = g(x)
5- мысал. х-3
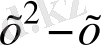 =(x-3)
2
теңдеуін шешейік.
=(x-3)
2
теңдеуін шешейік.
Шешуі. Мұнда ММЖ (мүмкін мәндер жиыны) х
 3 теңсіздігімен анықталады. (х-3)
2
=х-3
2
теңдігін ескерсек, онда жоғарыда айтылғандай, бұл теңдеу lnх-3=0 және х
2
-х-2=0 теңдеулер жиынтығына мәндес.
3 теңсіздігімен анықталады. (х-3)
2
=х-3
2
теңдігін ескерсек, онда жоғарыда айтылғандай, бұл теңдеу lnх-3=0 және х
2
-х-2=0 теңдеулер жиынтығына мәндес.
Бірінші теңдеуден х-3=1⇒ х 1 =2 және х 2 =4, ал екінші теңдеуден х 2 -х-2=0 ⇒ х 3 =-1, х 4 =2. Жауабы : -1; 2; 4.
Көрсеткіштік теңдеулер жүйесін шешу
Енді көрсеткіштік теңдеулер жүйесін шешуге мысал қарастырайық.
6-мысал.
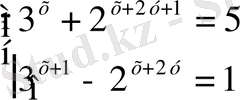
жүйесін шешейік.
Шешуі. Берілген жүйені
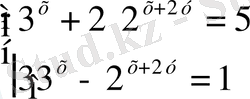
түрінде жазып 3 х =u, 2 х+2y =v белгілеулерін енгізу арқылы оны
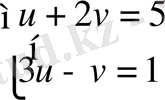
түріне келтіреміз. Онда u=1, v=2⇒ 3 х =1, 2 х+2y =2⇒х=0, х+2у=1. Осыдан х=0, у=0, 5 болып есептің жауабы шығады.
7-мысал.
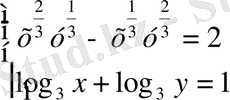
жүйесін шешу керек.
Шешуі. ММЖ х>0, y>0 теңсіздіктерімен анықталады. Осы жиында
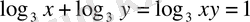
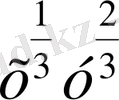 ху=3 теңдігі орындалады. Енді
ху=3 теңдігі орындалады. Енді
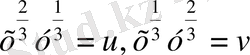 белгілеулерін енгізсек, онда uv=
белгілеулерін енгізсек, онда uv=
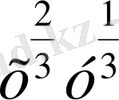
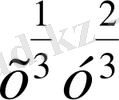 =xy=3 теңдігін аламыз. Онда берілген жүйені
=xy=3 теңдігін аламыз. Онда берілген жүйені
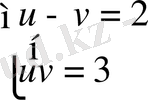 түрінде жазуға болады. Оның шешімдері u
1
=3, v
1
=1 және u
2
=-1, v
2
=-3. Осыдан u=3, v=1 деп алып
түрінде жазуға болады. Оның шешімдері u
1
=3, v
1
=1 және u
2
=-1, v
2
=-3. Осыдан u=3, v=1 деп алып
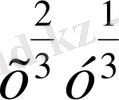 =3,
=3,
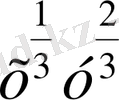 =1⇒(ху)
=1⇒(ху)
 х
х
 =3, ⇒(ху)
=3, ⇒(ху)
 х
х
 =1 теңдіктерін аламыз. ху=3 болғандықтан
=1 теңдіктерін аламыз. ху=3 болғандықтан
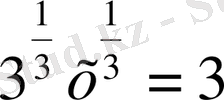 ,
,
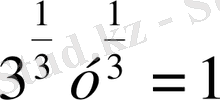 ⇒ х
1
=9, у
1
=
⇒ х
1
=9, у
1
=

Осы сияқты u=-1, v=-3 болғанда
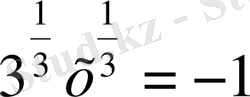 ,
,
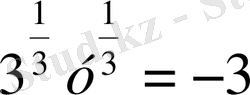 ⇒ х
2
= -
⇒ х
2
= -
 , у= - 9. Жүйенің ММЖ ны х>0, y>0 болғандықтан, есептің жауабы х=9, у=
, у= - 9. Жүйенің ММЖ ны х>0, y>0 болғандықтан, есептің жауабы х=9, у=

Көрсеткіштік теңсіздіктер
Көрсеткіштік функцияның қасиеттерінен:
- егер а>0 болса, онда u>v⇔au> avтеңсіздігінің;
- егер 0<а<1 болса, онда u>v⇔au< avтеңсіздігінің орындалатыны шығады.
Сонымен a
х
> b түрінде берілген қарапайым теңсіздіктерді a
х
> а
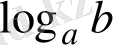 түріне келтіріп шешеді. Енді осыған бірер мысалдар келтірейік.
түріне келтіріп шешеді. Енді осыған бірер мысалдар келтірейік.
8-мысал.
9 х -10⋅3 х +9≤0 теңсіздігін шешейік
3
х
=у белгілеуін енгізе отырып, берілген теңсіздікті у
2
-10у+9≤0 түрінде жазамыз. Бұл теңсіздіктің шешуі 1≤у≤9 болғандықтан, х айнымалысы үшін 1≤3
х
≤9 теңсіздігін аламыз. Осыдан 3
0
≤3
х
≤3
2
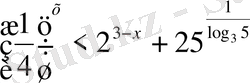 0≤х≤2. Жауабы [0; 2]
0≤х≤2. Жауабы [0; 2]
9-мысал.
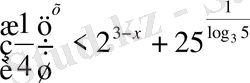 теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі.
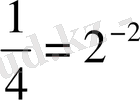 және 25
және 25
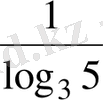 =9 болғандықтан, берілген теңсіздікті
=9 болғандықтан, берілген теңсіздікті
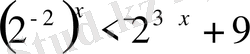 ⇒2
-2х
-8⋅2
-х
-9<0 түрінде жазып 2
-х
=у белгілеуін енгіземіз. Онда у
2
-8у-9<0⇒-1<y<9 теңсіздігін аламыз. Мұнда 2
-х
=у>0 болғандықтан 2
-х
<9⇒-x<log
2
9⇒- log
2
9<x болады. Жауабы: (- log
2
9; +∞)
⇒2
-2х
-8⋅2
-х
-9<0 түрінде жазып 2
-х
=у белгілеуін енгіземіз. Онда у
2
-8у-9<0⇒-1<y<9 теңсіздігін аламыз. Мұнда 2
-х
=у>0 болғандықтан 2
-х
<9⇒-x<log
2
9⇒- log
2
9<x болады. Жауабы: (- log
2
9; +∞)
10 мысал
3
х-
1>
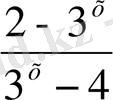 теңсіздігін шешейік
теңсіздігін шешейік
Шешуі Мұнда 3
х
=у деп аламыз,
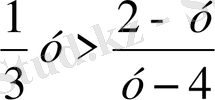 ⇔
⇔
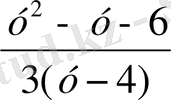 >0 ⇔
>0 ⇔
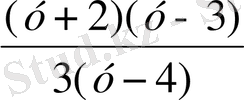 >0 теңсіздігін аламыз. Оның шешуі: у
>0 теңсіздігін аламыз. Оның шешуі: у
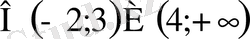
Карточка №1
- Туындыны тап
2.
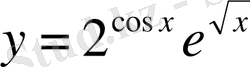
3. Мына қисықтармен шектелген фигураның ауданын тап
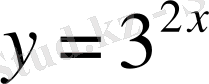



Карточка №2
- Туындыны тап
2.
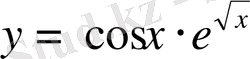
3. Мына қисықтармен шектелген фигураның ауданын тап
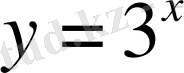
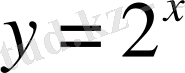

Карточка №3
- Туындыны тап
2.
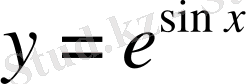
3.
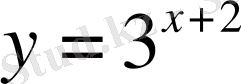 ,
,
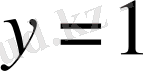

 сызықтармен шектелген фигураның ауданын тап.
сызықтармен шектелген фигураның ауданын тап.
Тест (теңдеу, теңсіздікке)
1 - нұсқа
1.

А) 5 В) 3 С) 2 Д) 0
2.
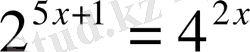
А) 0 В) 3 С) -1 Д) 5
3.
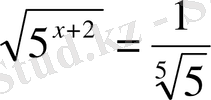
А) -3 В) 4 С)
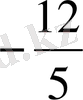 Д) 1
Д) 1
4.
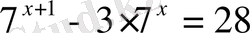
А) 1 В) -1 С) 0, 5 Д) 3
5.
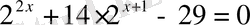
А) 1 В) -3 С) -2 Д) 0
6.
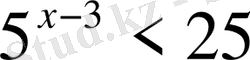
А)
 В)
В)
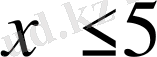 С)
С)
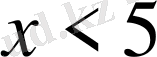 Д)
Д)

7.
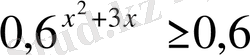
А)
 В)
В)
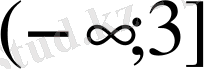 С)
С)
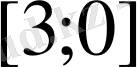 Д)
Д)
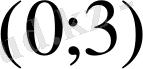
8.
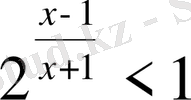
А)
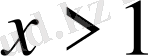 В)
В)
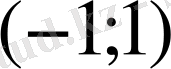 С)
С)
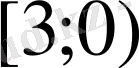 Д)
Д)
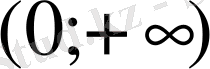
9.
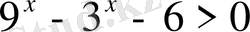
А)
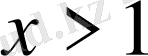 В)
В)
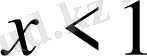 С)
С)
 Д)
Д)

10.
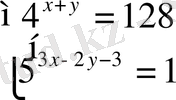
А)
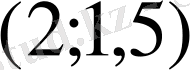 В)
В)
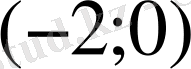 С)
С)
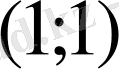 Д)
Д)
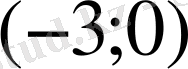
Тест (теңдеу, теңсіздікке)
2 - нұсқа
1.

А) 4 В) 3 С) 2 Д) 0
2.
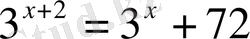
А) 1 В) 2 С) 3 Д) -2
3.
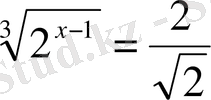
А) 1 В) 2, 5 С) 3 Д) 0, 5
4.
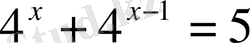
А) 2 В) 0, 5 С) -1 Д) 1
5.
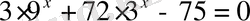
А) -3 В) 0 С) 1 Д) 2
6.
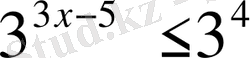
А)
 В)
В)
 С)
С)
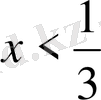 Д)
Д)
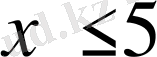
7.
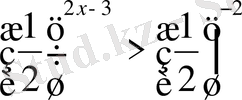
А)
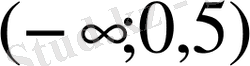 В)
В)
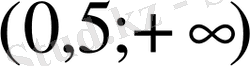 С)
С)
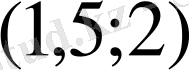 Д)
Д)
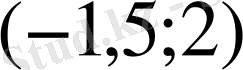
8.
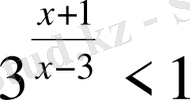
А)
 В)
В)
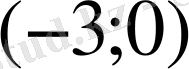 С)
С)
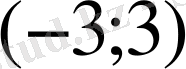 Д)
Д)
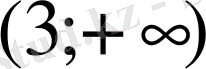
9.
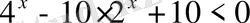
А)
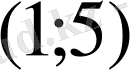 В)
В)
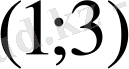 С)
С)
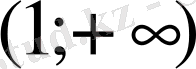 Д)
Д)

10.
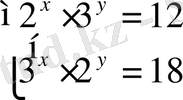
А)
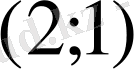 В)
В)
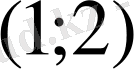 С)
С)
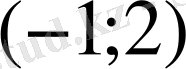 Д)
Д)
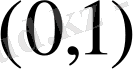
Өзіндік жұмыс
1 - нұсқа 2 - нұсқа
1.
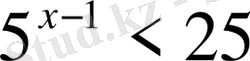
2.
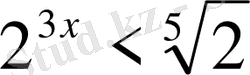
3.
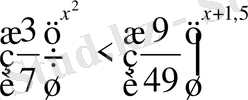
1.
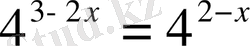
2.
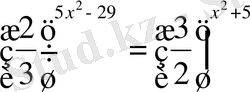
3.
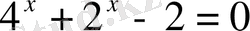
1.
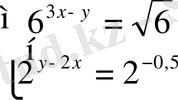
2.
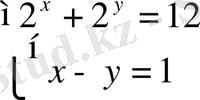
1.
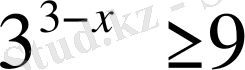
2.

3.
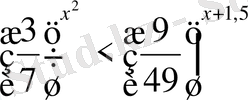
1.
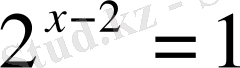
2.
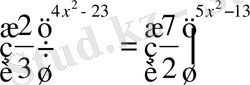
3.
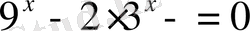
1.
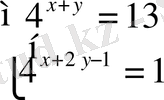
2.
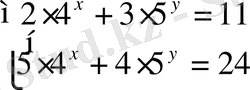
Карточка
(Қорытынды сабаққа)
А)
1.
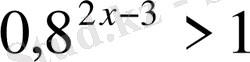
2.
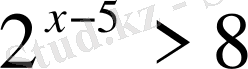
3.
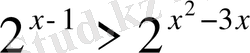
В)
1.
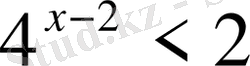
2.
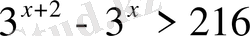
3.
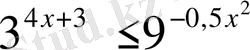
С)
1.
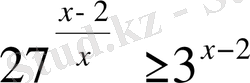
2.
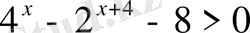
3.
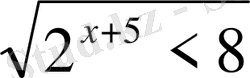
А)
1.
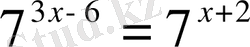
2.
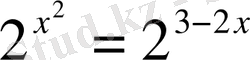
3.
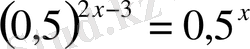
В)
1.
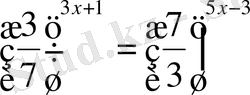
2.
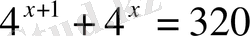
3.
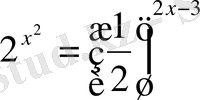
С)
1.
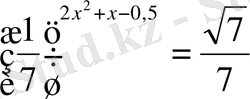
2.
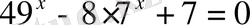
3.
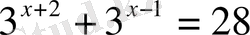
Логарифмдық және көрсеткіштік функцияларының туындысы
(тест) (90 мин - 11 сынып)
1- нұсқа
1.
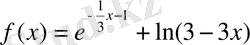 функциясының
функциясының
 табыңдар
табыңдар
а)
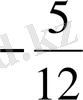 ; б)
; б)
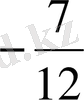 ; в)
; в)
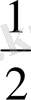 ; г)
; г)
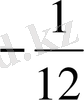
2. Егер
 болса,
болса,
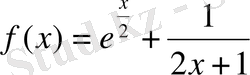 функциясы үшін
функциясы үшін
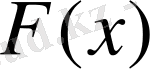 алғашқы функциясын табыңдар
алғашқы функциясын табыңдар
а)
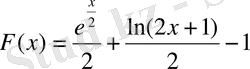 ;
;
б)
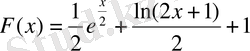 ;
;
в)
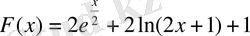 ;
;
г)
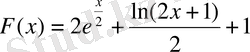 .
.
3.
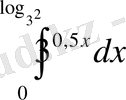 есептеңдер
есептеңдер
а)
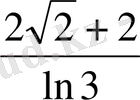 ;
;
б)
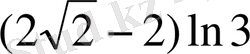 ;
;
в)
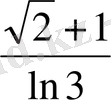 ;
;
г)
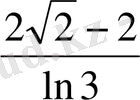 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz