Векторлар теориясы және геометриялық есептерде қолданылуы


МАЗМҰНЫ
1. ВЕКТОРЛАР ТУРАЛЫ ТҮСІНІК . . .
1. 1 Векторларға амалдар қолдану . . .
1. 2 Векторларды жіктеу тәсілдері . . .
2 ВЕКТОРЛАРДЫ ГЕОМЕТРИЯЛЫҚ ЕСЕП ШЫҒАРУДА ҚОЛДАНУ
2. 1 Планиметриялық есептерді шығаруда қолдану . . .
2. 2 Стереометриялық есептерді шығаруда қолдану . . .
ҚОРЫТЫНДЫ . . .
ӘДЕБИЕТТЕР ТІЗІМІ . . .
1 ВЕКТОР ТУРАЛЫ ТҮСІНІК
- Векторларға амалдар қолдану
Ғылым мен техникада кездесетін кейбір шамалар тек сан мәнімен ғана сипатталады (абсолют шамасымен) . Мысалы, масса, уақыт, температура және т. б. Бұл шамаларды скаляр шамалар деп атайды. Ал, кейбір шамалар сан мәнімен ғана емес, сонымен қатар бағытымен де сипатталады. Мысалы: жылдамдық, үдеу, күш, импульс жәке т. б. Бүл - векторлық шамалар.
Бір қызығы, жоғарыда аталған барлық векторлық шамалар механикада кездеседі. Алайда механиканың дамуы кезінде векторлық анализ тіпті болмаған. Векторлық анализ тек Максвелдің электромагниттік теориясынан кейін ғана пайда болды. Себебі, электр және магнит өрістерінің табиғаты - векторлық. [5, 7]
Кез-келген вектордын ұзындығы (вектордың шамасына пропорционал) мен бағыты болады. Векторларды қосу ережелері:
1) Үш бұрыш ережесі
1-сурет
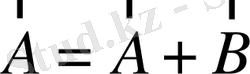 (1. 1)
(1. 1)
2) Параллелограмм ережесі:
2-сурет
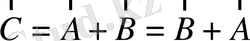 (1. 2)
(1. 2)
Векторлар - координаталар жүйелеріне тәуелсіз геометриялық объектер. Мысалы А-векторы (3-сурет) . Координаталар жүйесінің басынан басталып.
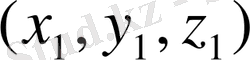
3-сурет
нүктесінде аяқталады.
 -
импульс, күш, жылдамдық
-
импульс, күш, жылдамдық
болуы мүмкін. Ал координаталар жүйесінің басынан
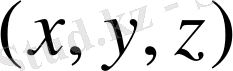 нүктесіне дейінгі арақашықтықты арнайы
нүктесіне дейінгі арақашықтықты арнайы
 -(радиус-вектор) символымен белгілейді:
-(радиус-вектор) символымен белгілейді:
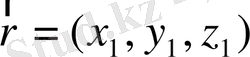 (1. 3)
(1. 3)
 -радиус-вектордың абсолют шамасы болсын. Демек,
-радиус-вектордың абсолют шамасы болсын. Демек,
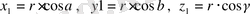 (1. 4)
(1. 4)
Мұндағы
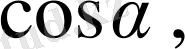
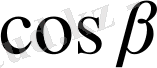 және
және
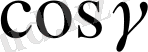 -
бағыттаушы косинустар деп аталады, ал
-
бағыттаушы косинустар деп аталады, ал
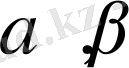 және
және
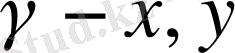 және
және
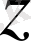 осьтерінің оң бағыты мен
осьтерінің оң бағыты мен
 - векторының араларындағы бұрыш (4-сурет)
- векторының араларындағы бұрыш (4-сурет)
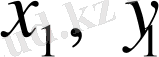 және
және
 шамаларын
шамаларын
 - радиус векторының (декарттық) компоненттері немесе проекциялары деп атайды.
- радиус векторының (декарттық) компоненттері немесе проекциялары деп атайды.
4 -сурет
Кез -келген
 векторын компоненттерге жіктеуге болады:
векторын компоненттерге жіктеуге болады:
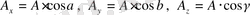 (1. 5)
(1. 5)
Енді
 және
және
 - бірлік векторларын енгізейік. Олардың ұзындықтары бірге тең және бағыттары
- бірлік векторларын енгізейік. Олардың ұзындықтары бірге тең және бағыттары
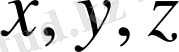 остерімен бағыттас болсын. Онда,
остерімен бағыттас болсын. Онда,
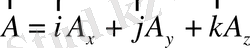 (1, 6)
(1, 6)
Егер
 = 0 болса. онда Пифагор
= 0 болса. онда Пифагор
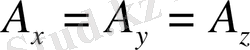 теоремасы бойынша
теоремасы бойынша
 векотырының абсолют шамасы:
векотырының абсолют шамасы:
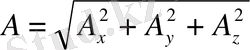
Бізге
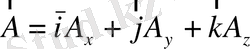 және
және
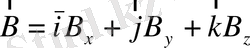 векторы берілсін, онда
векторы берілсін, онда
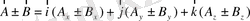 (1. 7)
(1. 7)
Координаталар жүйесінің бұрылуы
 радиус-векторды пайдаланып, вектордың жңна анықтамасын берейік. Оған физикалық себептер бар. Біз математика көмегімен табиғатты сипаттаймыз, сондықтан физикалық сипаттауымыз математикалық аппаратқа тәуелсіз болуы керек. Егер физикалық теорияны үй деп қарастырсақ, онда математика құрылыс саймандары. Саймандарсыз құрылыс жүргізе алмаймыз. Кұрылыс бітіргенде саймандарды жинастырып коямыз.
радиус-векторды пайдаланып, вектордың жңна анықтамасын берейік. Оған физикалық себептер бар. Біз математика көмегімен табиғатты сипаттаймыз, сондықтан физикалық сипаттауымыз математикалық аппаратқа тәуелсіз болуы керек. Егер физикалық теорияны үй деп қарастырсақ, онда математика құрылыс саймандары. Саймандарсыз құрылыс жүргізе алмаймыз. Кұрылыс бітіргенде саймандарды жинастырып коямыз.
Кеңістікті изотропты деп қарастырайык. Демек, зерттелетін физикалық жүйеміз немесе физикалық заң координаталар жүйесінің бағыттарына тәуелсіз.
 радиус-векторын екі жүйеде қарастырайық, х және у осьтерін сағат тілінің бағытына қарама қарсы бағытта
радиус-векторын екі жүйеде қарастырайық, х және у осьтерін сағат тілінің бағытына қарама қарсы бағытта
 бұрышына бұралық (5-сурет) . Пайда болған осьтерді х' және у' деп белгілейік. Сонда,
бұрышына бұралық (5-сурет) . Пайда болған осьтерді х' және у' деп белгілейік. Сонда,
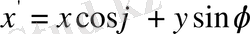 ,
,
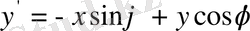 (1. 8)
(1. 8)
Егер
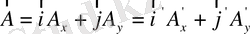 , онда,
, онда,
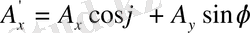 б
б
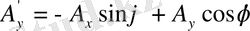 (1. 9) - координаталар жүйесін бұрған кездегі векторлық компоненттерінің түрлену заңы. Егер
(1. 9) - координаталар жүйесін бұрған кездегі векторлық компоненттерінің түрлену заңы. Егер
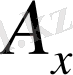 және
және
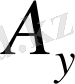 екі өлшемді радиус-вектор компоненттері сияқты түрлендірілетін болса, онда олар
екі өлшемді радиус-вектор компоненттері сияқты түрлендірілетін болса, онда олар
 векторының компоненттері болады. Егер
векторының компоненттері болады. Егер
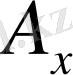 және
және
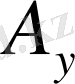 басқаша түрлендірілсе, онда бұлардан вектор кұруға болмайды. Түсінікті болу үшін (1. 9) тендеуіндегі
басқаша түрлендірілсе, онда бұлардан вектор кұруға болмайды. Түсінікті болу үшін (1. 9) тендеуіндегі
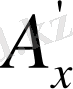 және
және
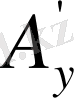 шамаларының мағынасын ізделік. А векторы координаттар және кез келген
шамаларының мағынасын ізделік. А векторы координаттар және кез келген
 векторының компоненттерінің функциясы болсын:
векторының компоненттерінің функциясы болсын:
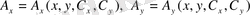 (1. 10)
(1. 10)
Бұрылған кездегісі:
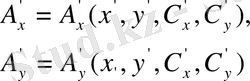 (1. 11)
(1. 11)
(1. 8) теңдеуін пайдаланып,
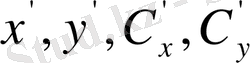 координаттарын бұрылмаған координаталар жүйесі мен
координаттарын бұрылмаған координаталар жүйесі мен
 бұрышы арқылы сипаттауға болады. Алайда бұрышқа тәуелділік түсінік кеңістіктің изотроптылығына кайшы келеді. Сондықтан бағытка тәуелсіз функциялармен шектелейік. Егер
бұрышы арқылы сипаттауға болады. Алайда бұрышқа тәуелділік түсінік кеңістіктің изотроптылығына кайшы келеді. Сондықтан бағытка тәуелсіз функциялармен шектелейік. Егер
 болса, онда
болса, онда
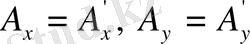 .
.
Мысалы:
1. Екі шама берілген (-у, х) . Екі өлшемді вектор құруға болатынын көрсетіңдер.
Жүйені
 бүрышына бұрғанда осы шамалардың түрленуін қарастырайық.
бүрышына бұрғанда осы шамалардың түрленуін қарастырайық.
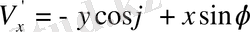 ,
,
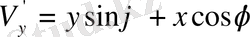
мұндағы
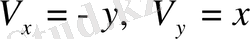 (1. 8) тендеуін пайдаланып.,
(1. 8) тендеуін пайдаланып.,
 және
және
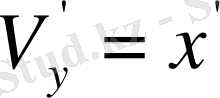 екенін көреміз.
екенін көреміз.
Яғни, (1. 9) тендеуін қанағаттандырады. Демек. (-у, х) жұбы вектор компоненттері.
2.
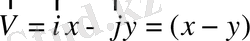 қарастырайық (1. 9) теңдеуіне байланысты
қарастырайық (1. 9) теңдеуіне байланысты
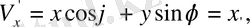
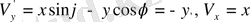 және
және
 ,
,
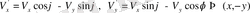 вектор бола алмайды. Осы теңдіктерді басқа түрде жазайық:
вектор бола алмайды. Осы теңдіктерді басқа түрде жазайық:
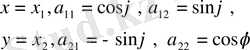 (1. 12)
(1. 12)
(1. 9) тендеуі:
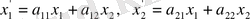 (1. 13)
(1. 13)
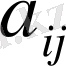 коэффициенттерін бағыттаушы косинустар деп қарастыруға болады.
(
коэффициенттерін бағыттаушы косинустар деп қарастыруға болады.
(
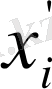 және
және
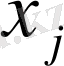 , араларындағы бұрыш) ;
, араларындағы бұрыш) ;
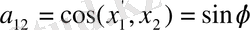
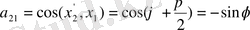
(1. 13) теңдеуін қысқаша былай жазуға болады:
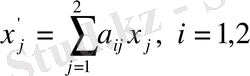 (1. 14)
(1. 14)
Енді осы айтылғандарды 3, 4 және одан көп
өлшемдер үшін оңай жазуға болады.
 -өлшемі
-өлшемі

векторының
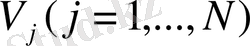 компоненттерімен анықталады, егер осы шамалар басқа (бұрылған) жүйеде мына теңдеумен берілсе:
компоненттерімен анықталады, егер осы шамалар басқа (бұрылған) жүйеде мына теңдеумен берілсе:
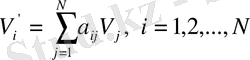 (1. 15)
(1. 15)
мұндағы
 және
және
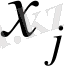 араларындағы бұрыш.
араларындағы бұрыш.
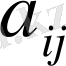 коэффициентінің анықтамасынан декарттық координаттарда былай жазуға болады:
коэффициентінің анықтамасынан декарттық координаттарда былай жазуға болады:
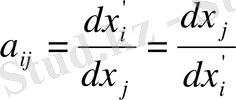 (1. 16)
(1. 16)
Бұл дербес туындылар (1. 16) теңдеуін (1. 15) теңдеуіне қоялық:
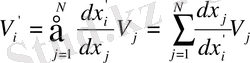 (1. 17)
(1. 17)
Бағыттаушы косинустар
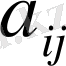 ортогональдық шарттарын қанағаттандырады.
ортогональдық шарттарын қанағаттандырады.
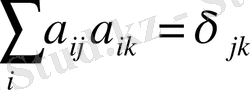 (1. 18)
(1. 18)
немесе
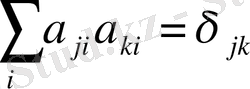 (1. 19)
(1. 19)
Мүндағы
 - Кронекер символы,
- Кронекер символы,
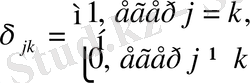 (1. 20)
(1. 20)
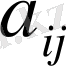 мәндерін (1. 12) тендеуінен (1. 18) және (1. 19) тендеулеріне қойсақ, онда белгілі тендеуді аламыз:
мәндерін (1. 12) тендеуінен (1. 18) және (1. 19) тендеулеріне қойсақ, онда белгілі тендеуді аламыз:
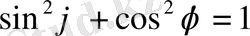
(1. 18) теңдеуінің дұрыстығына көз жеткізу үшін (1. 16) өрнегін пайдаланалық:
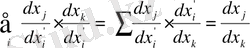 (1. 21)
(1. 21)
Қорытынды. Вектордың компоненттерін түрлендіру заңдарының жаңа анықтамасынан 2 жағдай шығады:
- Әртүрлі физикалық кұбылыстарды сипаттауға қолайлы;
- Математиканың жаңа бөлімі-тензорлық талдауға көшуге мүмкіндік береді.
Жаттығулар:
1. Тұрақты
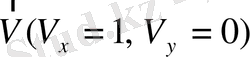 вектор берілген.
вектор берілген.
Бұрылған координаталар жүйесінде
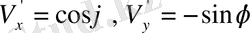 екенін көрсетіңіздер. (Тұракты вектор енгізу арқылы, біз бір бағытты көрсеттік) .
екенін көрсетіңіздер. (Тұракты вектор енгізу арқылы, біз бір бағытты көрсеттік) .
2. Келесі шамалар векторлық түрлендіру заңын (з. т. з. ) (1. 15) қанағаттандыра ма?
а) (х - у, х+у, 0) векторын z осінен бұрғанда;
б) (0, 2 z+у, z - 2у) векторын х осі бойынша бұғанда;
в) ( у 1 + z 2 , - ху, - хz ) векторын барлық осьтер бойынша бұрғанда;
3.
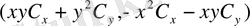 вектор болатынын дәлелдеңздер. С
х
және С
у
шамалары тұрақты
вектор болатынын дәлелдеңздер. С
х
және С
у
шамалары тұрақты
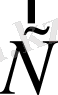 векторының компоненттері .
векторының компоненттері .
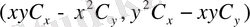 шамалары үшін де тексеріңіздер.
шамалары үшін де тексеріңіздер.
4. Барлық осьтер бойынша бұруды зерттеп, мына сұрақка жауап беріңіздер:
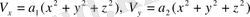 және
және
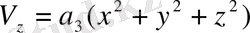
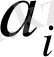 тұрақтыдар) шамалары вектор компоненттері бола ала ма?
тұрақтыдар) шамалары вектор компоненттері бола ала ма?
5. Екі өлшемді
 векторы (ах+bу, сх+dy) түрінде берілген, мұндағы
векторы (ах+bу, сх+dy) түрінде берілген, мұндағы
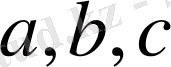
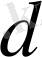 -тұрақты сандар.
-тұрақты сандар.
 векторынын радиал
векторынын радиал
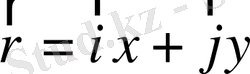 және тангенциал векторларының сызықты комбинациясы болатынын дәлелденіздер:
және тангенциал векторларының сызықты комбинациясы болатынын дәлелденіздер:
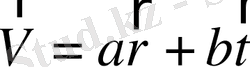
Ескерту. Векторлық түрлендіру заңы кез-келген бұрыш және кез-келген нүкте (х, у) орындалады.
Скаляр көбейтінді
Векторлардың математикалық көбейту зандары бір-біріне қайшы келмеуі керек. Барлық мүмкін болатын анықтамалар ішінен физикаға және математикаға қатысты қажетті екі анықтаманы тандалық. Үшінші тарауда басқа анықтама беріледі.
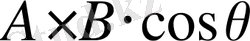 көбейтіндісі физикада жиі кездеседі.
көбейтіндісі физикада жиі кездеседі.
Мүндағы, А, В - екі вектордың абсолют шамалары, Ө - олардың арасындағы бұрыш.
Мысалы: жұмыс =күш х жол х соsӨ.
Скаляр көбейтіндіні анықтайық (
 және
және
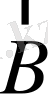 - векторы үшін) :
- векторы үшін) :
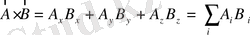 (1. 22)
(1. 22)
(1. 22)
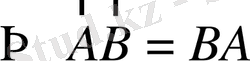
Бірлік векторлар үшін:
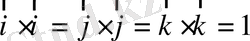 (1. 22а)
(1. 22а)
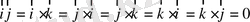 (1. 22в)
(1. 22в)
Егер осьтерді қайта бағыттап, х осін
 векторы бойынша бағыттасақ, онда
векторы бойынша бағыттасақ, онда
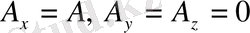 және
және
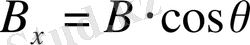 (1. 22)
(1. 22)
6-сурет
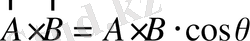 (1. 23)
(1. 23)
Егер
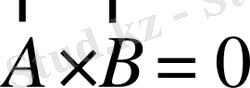 және
және
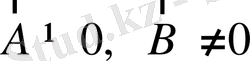 болса, онда (1. 22)
болса, онда (1. 22)
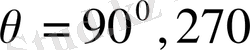 және т. с.
және т. с.
Басқаша айтқанда,
 және
және
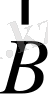 - ортогонал векторлар.
- ортогонал векторлар.
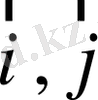 және
және
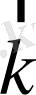 векторлары да өзара ортогонал.
векторлары да өзара ортогонал.
7-сурет
Ортогоналдық түсінігін жалғастыралық,
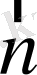 -
бірлік векторы болсын, ал
-
бірлік векторы болсын, ал
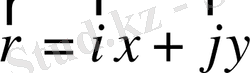 -нөлдік
емес, ху жазықтығында жататын вектор. Егер
-нөлдік
емес, ху жазықтығында жататын вектор. Егер
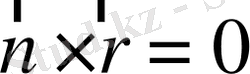 болса, онда мұндағы
болса, онда мұндағы
 - кез-келген вектор, онда
- кез-келген вектор, онда
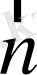 векторы ху жазықтығына перпендикуляр (7-сурет) .
векторы ху жазықтығына перпендикуляр (7-сурет) .
Енді скаляр көбейтіндінің скаляр шама екенін дәлелдейік. Ол үшін
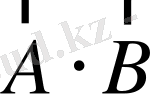 көбейтіңдісін координаталар жүйесін бұру арқылы зерттейік. (1. 15) теңдеуінің арқасында:
көбейтіңдісін координаталар жүйесін бұру арқылы зерттейік. (1. 15) теңдеуінің арқасында:
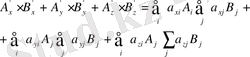 (1. 24)
(1. 24)
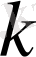 және
және
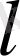 индекстерін пайдаланып, қысқаша жазалық: векторының өз-өзіне көбейтіндісін қарастырайық:
индекстерін пайдаланып, қысқаша жазалық: векторының өз-өзіне көбейтіндісін қарастырайық:
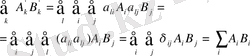 (1. 25) , (1. 26)
(1. 25) , (1. 26)
Сонымен
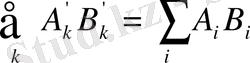 (1. 27)
(1. 27)
Скаляр шама, координаталар жүйесін бұруға инвариантты.
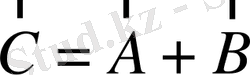 векторының өз-өзіне көбейтіндісін қарастырайық:
векторының өз-өзіне көбейтіндісін қарастырайық:
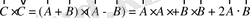 (1. 28)
(1. 28)
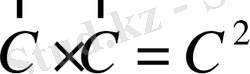 (1. 29)
(1. 29)
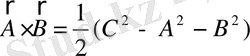 (1. 30)
(1. 30)
А • В -координаталар жүйесін бұруға инвариантты, себебі (1. 30) теңдеуінің оң жағы скаляр шама. (1. 28) тендеуін қайта. басқа түрде жазалық:
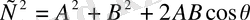 (1. 31)
(1. 31)
8-сурет
косинустар заңы. (1. 28) және (1. 31) теңдеуін салыстырып, косинустар заңының векторлық табиғатын байқаймыз (8-сурет) .
Векторлық көбейтінді
Бұл көбейтіндіде екі вектордың арасындағы бұрыштың синусын пайдаланады.
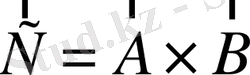 (1. 32)
(1. 32)
мұндағы,
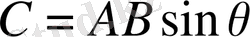 ,
бірақ мұндағы
,
бірақ мұндағы
 -вектор, және ол
-вектор, және ол
 және
және
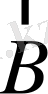 векторлар жатқан жазықтыққа перпендикуляр.
векторлар жатқан жазықтыққа перпендикуляр.
 ,
,
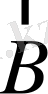 және
және
 оң координаттар жүйесін құрасын, онда
оң координаттар жүйесін құрасын, онда
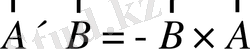 (коммут. емес) . (1. 32а)
(коммут. емес) . (1. 32а)
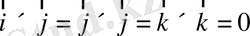 (1. 326)
(1. 326)
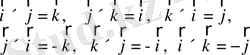 (1. 32в)
(1. 32в)
Векторлық көбейтіндінің маңызды геометриялық қасиеті бар (9-сурет) .
9-сурет
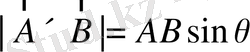 -
параллелограмм ауданы.
-
параллелограмм ауданы.
Сонымен,
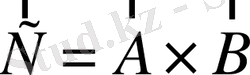 векторы параллелограмм жазықтығына перпендикуляр, ал абсолют шамасы осы параллелограмның ауданына тең болады екен.
векторы параллелограмм жазықтығына перпендикуляр, ал абсолют шамасы осы параллелограмның ауданына тең болады екен.
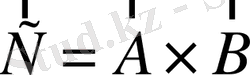 векторлық көбейтіндінің басқа анықтамасы.
векторлық көбейтіндінің басқа анықтамасы.
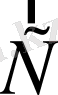 -векторының компоненттері:
-векторының компоненттері:
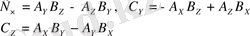 (1. 33)
(1. 33)
және
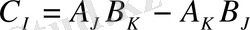
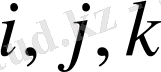 - әртүрлі.
- әртүрлі.
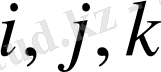 - индекстерін циклді өзгерту қажет.
- индекстерін циклді өзгерту қажет.
Векторлық көбейтіндіні анықтауыш ретінде жазған ыңғайлы:
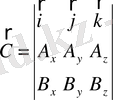 (1. 35)
(1. 35)
(1. 32) және (1. 33) көбейтіңділердің эквиваленттілігін көрсетейік. Ол үшін
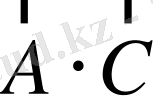 және
және
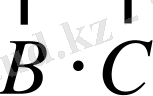 көбейтінділерін қарастырайық.
көбейтінділерін қарастырайық.
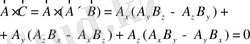 (1. 36)
(1. 36)
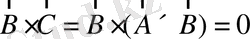 (1. 37)
(1. 37)
=> (1. 36) және (1. 37) теңдеулерінен С векторы А векторына да, В векторына да перпендиқуляр. А және В векторлары тиісті жазықтыққа перпендикуляр.
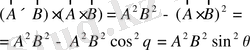 (1. 38)
(1. 38)
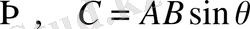 (1. 39)
(1. 39)
(1. 38) теңдеуінде
 көбейтіндісін (1. 33) теңдеуі бойынша компоненттерге жіктедік, содан кейін (1. 22) скаляр көбейтіндісін пайдаландық. (1. 36), (1. 37) және (1. 39) теңдеулерінен (1. 32) және (1. 33) анықтамалары эквивалентті екендігі шығады.
көбейтіндісін (1. 33) теңдеуі бойынша компоненттерге жіктедік, содан кейін (1. 22) скаляр көбейтіндісін пайдаландық. (1. 36), (1. 37) және (1. 39) теңдеулерінен (1. 32) және (1. 33) анықтамалары эквивалентті екендігі шығады.
Енді
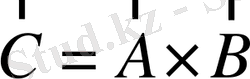 вектор екенін керсетейік (яғни, вектордың түрлендіру заңына бағынатынын) . Бұрылған координаталар жүйесінде:
вектор екенін керсетейік (яғни, вектордың түрлендіру заңына бағынатынын) . Бұрылған координаталар жүйесінде:
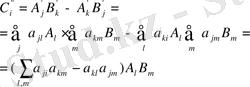 (1. 40)
(1. 40)
мұндағы.
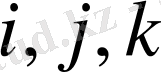 - циклдік ретте алуға тиіспіз.
- циклдік ретте алуға тиіспіз.
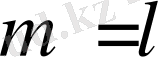 болғанда (1. 40) теңдеуі нөлге тең.
болғанда (1. 40) теңдеуі нөлге тең.
 болсын, онда
болсын, онда
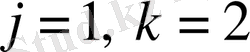 (циклдік рет) :
(циклдік рет) :
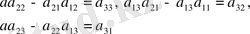 (1. 41)
(1. 41)
(1. 41) теңдеуін (1. 40) теңдеуіне қоялық:
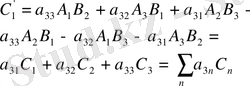 (1. 42)
(1. 42)
Осылай
 және
және
 үшін табамыз. Олар (1. 15) шартын қанағаттандырады. Яғни,
үшін табамыз. Олар (1. 15) шартын қанағаттандырады. Яғни,
 -векторлык шама болып табылады.
-векторлык шама болып табылады.
Жаттығулар:
1.
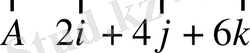 және
және
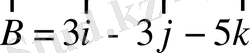 векторлары берілген.
векторлары берілген.
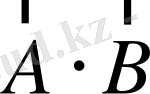 және
және
 көбейтінділерін табыңдар.
көбейтінділерін табыңдар.
2. Теңдікті дәлелдеңдер.


3. Үшбұрыш нүктелерінің координаттары берілген:
(2. 1, 5), (5, 2, 8) және (4, 8, 2) . Осы үшбұрыштың ауданын табыңыздар.
4.
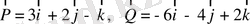 және
және
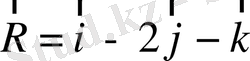
векторлары берілген. Қайсылары өзара перпендикуляр және қайсылары өзара не
 , не
, не
 ?
?
5.
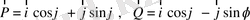
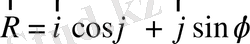 векторларын пайдаланып,
векторларын пайдаланып,
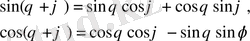
формулаларын дәлелдеңіздер.
6.
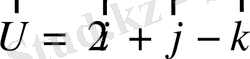 және
және
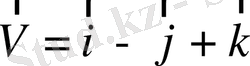 векторына перпендикуляр А векторын табыңыздар. А векторы бірлік вектор болу үшін қандай қосымша шарт керек?
векторына перпендикуляр А векторын табыңыздар. А векторы бірлік вектор болу үшін қандай қосымша шарт керек?
7.
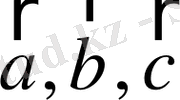 және
және
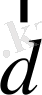 векторлары бір жазықтықта жатады,
векторлары бір жазықтықта жатады,
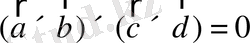 екенін көрсетіңіздер.
екенін көрсетіңіздер.
8. АВС сфералық үшбұрыштың бұрыштарын және жақтарын табыңыздар. Мұндағы
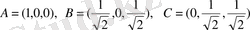 . Барлық векторлар координат басынан басталады. (10-сурет) .
. Барлық векторлар координат басынан басталады. (10-сурет) .
10-сурет
9. В магниттік индукция Лоренц теңдеуінен анықталады:
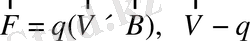 электр зарядының жылдамдығы,
электр зарядының жылдамдығы,
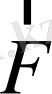 -зарядқа әсер ететін күш.
-зарядқа әсер ететін күш.
1)
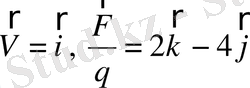
2)
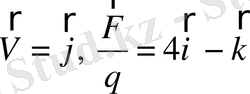
3)
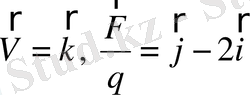
Осы үш тәжірибеден В векторды табу керек.
Жауабы:
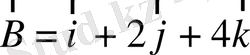
Үш вектордың аралас және 2-реттік векторлық көбейтінділері
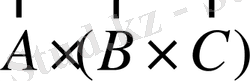 және
және
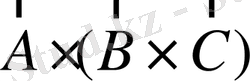 -
мұндай көбейтінділер комбинациясы жиі кездеседі. Біріншісін аралас көбейтінді деп атайды.
-
мұндай көбейтінділер комбинациясы жиі кездеседі. Біріншісін аралас көбейтінді деп атайды.
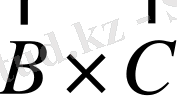 -
көбейтіндісінен шығатын векторлар
А
векторына көбейтіледі, демек скаляр шама шығады.
-
көбейтіндісінен шығатын векторлар
А
векторына көбейтіледі, демек скаляр шама шығады.
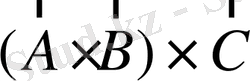 -
скаляр вектор, ал бүл операция белгісіз. Сондықтан оны әзірге қарастырмаймыз.
-
скаляр вектор, ал бүл операция белгісіз. Сондықтан оны әзірге қарастырмаймыз.
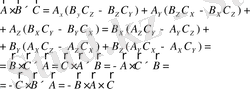 (1. 43)
(1. 43)
және т. с. с.
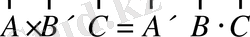 (1. 44)
(1. 44)
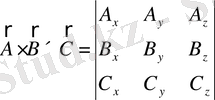 (1. 45)
(1. 45)
(1. 43) теңдігі жоғарғы ретті симметриялы (1. 45) тендігінен шығады. Үш вектордың аралас көбейтіндісінің геометриялық түсініктемесі бар. Ол: егер, А, В және С векторлары параллелепипедтің "қабырғалары" болса (11-сурет),
11-сурет
онда
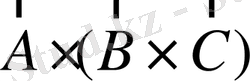 -
көбейтіндісінің шамасы осы параллелепипедтің көлеміне тең болады (әрине, аралас көбейтінді теріс санға да тең болуы мүмкін) .
-
көбейтіндісінің шамасы осы параллелепипедтің көлеміне тең болады (әрине, аралас көбейтінді теріс санға да тең болуы мүмкін) .
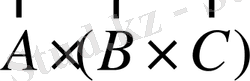 -
2 рет векторлық кебейтіндіні қарастырайық. Бұл жолы жақшаны сақтау керек
-
2 рет векторлық кебейтіндіні қарастырайық. Бұл жолы жақшаны сақтау керек
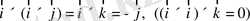 (1. 48)
(1. 48)
Демек, бұл көбейтіндіден
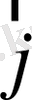 вектор шығады. Оның бағыты
А
және
(Вх
С) векторлары жататын жазықтыққа перпендикуляр.
вектор шығады. Оның бағыты
А
және
(Вх
С) векторлары жататын жазықтыққа перпендикуляр.
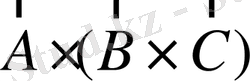 -
векторлары
В
және
С
векторлары тиісті жазықтықта жатады. Себебі, ВС жазықтығы
-
векторлары
В
және
С
векторлары тиісті жазықтықта жатады. Себебі, ВС жазықтығы
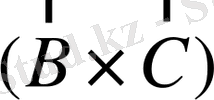 векторына перпендикуляр. Сондықтан,
векторына перпендикуляр. Сондықтан,
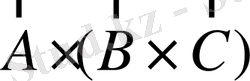 векторының компоненттері
В
және С векторларының сызықты комбинациясына байланысты:
векторының компоненттері
В
және С векторларының сызықты комбинациясына байланысты:
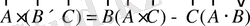 (1. 49)
(1. 49)
Аралас және 2-реттік векторлық көбейтінділер арқылы одан көп векторлар көбейтінділерін қысқартуға болады. Мысалы: Аралас көбейтінді кері кристалл торларын есептеуде пайдаланады.
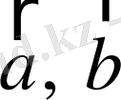 және
және
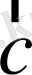 (міндетті түрде өзара перпендикуляр емес) - кристалл торларын анықтайтын векторлар болсын. Онда кез-келген 2 вектордың арақашықтығы
(міндетті түрде өзара перпендикуляр емес) - кристалл торларын анықтайтын векторлар болсын. Онда кез-келген 2 вектордың арақашықтығы
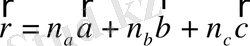 тендеуімен беріледі. Мұндағы,
тендеуімен беріледі. Мұндағы,
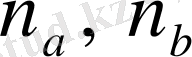 және
п
с
-
бүтін сандар.
және
п
с
-
бүтін сандар.
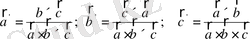 (1. 50)
(1. 50)
векторларын жазуға болады. (1. 50)
=>
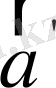 векторы (
векторы (
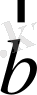 және
және
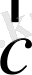 )
жазықтығына перпендикуляр, ал абсолют шамасы
)
жазықтығына перпендикуляр, ал абсолют шамасы
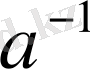 - ге пропорционал. Шынында.
- ге пропорционал. Шынында.
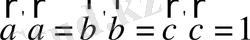
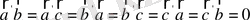
Соңғы тендеулер кері торларды анықтайды. Кері тор толқындардың кристалдағы әртүрлі жазықтықтарда шашырауын есептеуге қажет.
Жаттығулар
1.
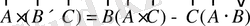 болатындығын дәледеңіздер.
болатындығын дәледеңіздер.
2.
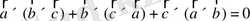 екенін көрсетіңіздер.
екенін көрсетіңіздер.
3.
 векторы
векторы
 . - радиалды және
. - радиалды және
 -
тангенсиалды векторларға жіктелген,
-
тангенсиалды векторларға жіктелген,
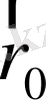 -
радиалды бағыттағы бірлік вектор.
-
радиалды бағыттағы бірлік вектор.
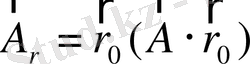 және
және
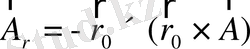 екенін көрсетіңіздер.
екенін көрсетіңіздер.
- Үш (нөлдік емес) А, Вжәне С векторларының компланарлығының қажетті және жеткілікті шарты болып, олардың аралас көбейтінділерінің нөлге теңдігі болып табылатындығын дәлелдеңіз:
- Үш вектор берілген.
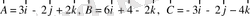
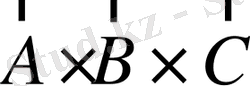 және
және
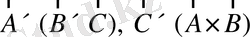 және
және
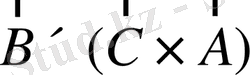 болатындығын табу керек.
болатындығын табу керек.
6.
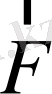 күші
күші
 нүктесінде орналасқан денеге әсер етеді. Координат басынан жүргізілген кез-келген оське қатысты қорытынды момент:
нүктесінде орналасқан денеге әсер етеді. Координат басынан жүргізілген кез-келген оське қатысты қорытынды момент:
 -
ға тең екенін көрсету керек. Мұндағы
а-
осы осьтің бағытындағы бірлік вектор.
-
ға тең екенін көрсету керек. Мұндағы
а-
осы осьтің бағытындағы бірлік вектор.
7.
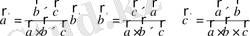
және
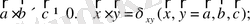
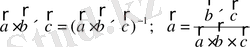 кендігін көрсету керек.
кендігін көрсету керек.
Векторлық талдау (векторларды дифференциалдау)
Градиент
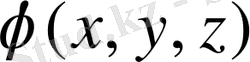 -скаляр функция болсын, яғни фуикция тек кеңістік нүктелерінің (
-скаляр функция болсын, яғни фуикция тек кеңістік нүктелерінің (
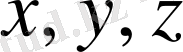 )
мәніне тәуелді. Скаляр болғандықтан кез келген координаталар жүйесінде белгілі бір нүкте үшін нақты мәні өзгермеуі тиіс, яғни:
)
мәніне тәуелді. Скаляр болғандықтан кез келген координаталар жүйесінде белгілі бір нүкте үшін нақты мәні өзгермеуі тиіс, яғни:
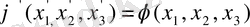 (1. 51)
(1. 51)
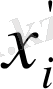 бойынша дифференциалдайық:
бойынша дифференциалдайық:
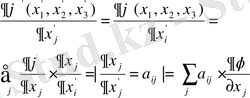 (1. 52)
(1. 52)
Бұл теңдіктерді мүшелеп қосамыз, сонда мынау шығады:
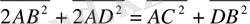
Параллелограмның қарама-қарсы қабырғалары тең болатындықтан, бұл теңдік- параллелограмм диагональдары квадраттарының қосындысы оның қабырғалары квадраттарының қосындысына тең- екенін білдіреді, дәлелдемекшіміз де осы болатын.
1. 2 Векторларды жіктеу тәсілдері
Векторларды координаттық осьтер бойынша жіктеу
Егер вектордың абсолют шамасы бірге тең болса, оны
бірлік вектор
деп атайды. Бағыты координаттың оң жарты осьтердің бағытындай бірлік векторлар
координаттық векторлар
немесе
орттар
деп аталады. Біз оларды
х
осі бойында
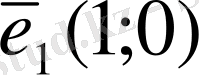 және
у
осі бойында
және
у
осі бойында
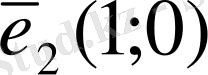 деп белгілейміз.
деп белгілейміз.
Ал координаттың векторлар нөлдік вектордан өзге және де коллинеар емес болатындықтан, кез келген
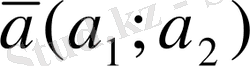 векторды осы векторлар бойынша жіктеуге болады:
векторды осы векторлар бойынша жіктеуге болады:
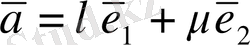 (*)
(*)
Осы жіктеудің
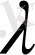 мен
мен
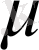 коэффициенттерің табамыз. Ол үшін (*) теңдіктің екі жақ бөлігін де
коэффициенттерің табамыз. Ол үшін (*) теңдіктің екі жақ бөлігін де
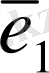 векторына көбейтеміз. Сонда
векторына көбейтеміз. Сонда
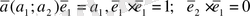 , ендеше
, ендеше
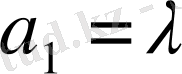
(*) теңдіктің екі жақ бөлігін де
е
2
векторына осылайша кебейтіп,
 екенін табамыз.
екенін табамыз.
Сонымен, кез келген
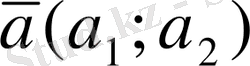 векторды былай жіктеуге болады:
векторды былай жіктеуге болады:
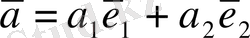
Сондықтан, егер
 болса, онда
В
нүктесі
ОА
жарты түзуінде жатады, ал одан болса,
болса, онда
В
нүктесі
ОА
жарты түзуінде жатады, ал одан болса,
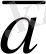 мен
мен
 векторлары бірдей бағытталады. Егер де
векторлары бірдей бағытталады. Егер де
 болса, онда
В
нүктесі толықтауыш жарты түзуде жатады да,
болса, онда
В
нүктесі толықтауыш жарты түзуде жатады да,
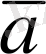 мен
мен
 векторлары қарама-қарсы бағытталады.
векторлары қарама-қарсы бағытталады.
 векторыньщ абсолют шамасы мынаған тең:
векторыньщ абсолют шамасы мынаған тең:
Теорема дәлелденді.
Есеп.
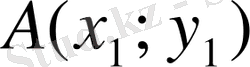 мен
мен
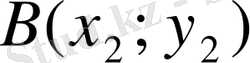 нүктелері берілген. Сонда АВ мен
ВА
векторларының қарама-қарсы бағытталғанын дәлелдеңдер.
нүктелері берілген. Сонда АВ мен
ВА
векторларының қарама-қарсы бағытталғанын дәлелдеңдер.
Шешуі.
АВ
векторының коордннаттары
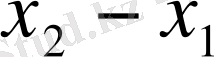 мен
мен
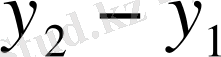 болады.
ВА
векторының координаттары
болады.
ВА
векторының координаттары
 мен
мен
 болады. Біз мынаны көріп отырмыз:
болады. Біз мынаны көріп отырмыз:
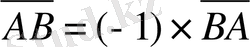 . Олай болса, АВ мен
ВА
векторлары қарама-қарсы бағытталған болып шығады. . [8, 7]
. Олай болса, АВ мен
ВА
векторлары қарама-қарсы бағытталған болып шығады. . [8, 7]
Векторды коллинеар емес екі вектор бойынша жіктеу
Бір түзу бойында немесе параллель түзулер бойында жатқан нөлдік емес екі вектор коллинеар векторлар деп аталадығ Коллинеар векторлар не бірдей багытталган болады, не қарама-қарсы бағытталған болады.
Айталық,
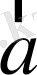 мен
мен
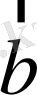 - нолден өзге коллинеар векторлар болсын. Сонда
- нолден өзге коллинеар векторлар болсын. Сонда
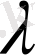 саны табылып
,
саны табылып
,
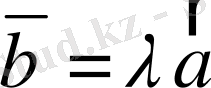
теңдігі орындалатынын дәлелдейік .
Айталық,
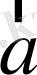 мен
мен
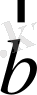 векторлары бірдей багытталған болсын. Сонда
векторлары бірдей багытталған болсын. Сонда
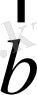 және
және
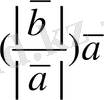 векторлары да бірдей бағытталған және олардың абсолют шамасы
векторлары да бірдей бағытталған және олардың абсолют шамасы
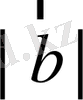 да бірдей болады. Демек. олар тең:
да бірдей болады. Демек. олар тең:
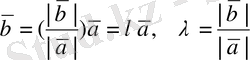
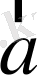 мен
мен
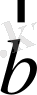 векторлары қарама-қарсы бағытталған болғанда былай тұжырымдаймыз:
векторлары қарама-қарсы бағытталған болғанда былай тұжырымдаймыз:
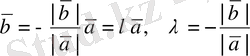
дәлелдемекшіміз де осы болатын.
Айталық,
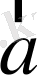 мен
мен
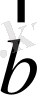 - нөлден өзге коллинеар емес векторлар болсын. Енді кез келген
- нөлден өзге коллинеар емес векторлар болсын. Енді кез келген
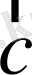 векторды
векторды
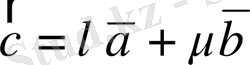
түрінде көрсетуге болатынын дәлелдейік.
Айталық,
А
мен
В -
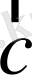 векторының басы мен ұшы болсын.
А
мен
В
нүктелері арқылы
векторының басы мен ұшы болсын.
А
мен
В
нүктелері арқылы
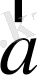 және
және
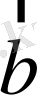 векторларына параллель түзулер жүргіземіз. Олар қандай да бір
С
нүктесінде қиылысады. Сонда:
векторларына параллель түзулер жүргіземіз. Олар қандай да бір
С
нүктесінде қиылысады. Сонда:

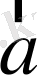 мен
мен
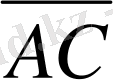 векторлары коллинеар болғандықтан,
векторлары коллинеар болғандықтан,
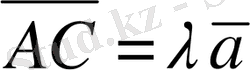 болады.
болады.
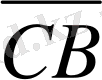 мен
мен
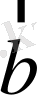 векторлары коллинеар болгандықтан,
векторлары коллинеар болгандықтан,
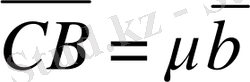 болады. Сонымен,
болады. Сонымен,
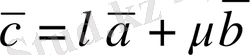 дәлелдемекшіміз де осы болатын.
дәлелдемекшіміз де осы болатын.
Векторлардың скаляр көбейтіндісі
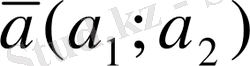 мен
мен
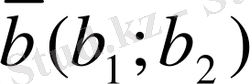 векторларының
скаляр көбейтіндісі
деп
векторларының
скаляр көбейтіндісі
деп
 санын атайды.
санын атайды.
Векторлардың скаляр көбейтіндісін де, сандарды көбейткендегідей, жазып орындайды,
 скаляр кебейтінді
скаляр кебейтінді
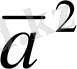 деп атайды. [11, 20]
деп атайды. [11, 20]
.
2 ВЕКТОРЛАРДЫ ГЕОМЕТРИЯЛЫҚ ЕСЕП ШЫҒАРУДА ҚОЛДАНУ
2. 1 Планиметриялық есептерді шығаруда қолдану
Мектеп көлемінде оқытылатын «Векторлар тақырыбы» күрделі тақырыптардың қатарына жатады. «Векторлар тақырыбын оқыту әдістемесін» сөз етер болсақ ІХ-сыныптың геометрия пәні бойынша өтетін алғашқы сабағы «Параллель көшіру және оның қасиеттері» тақырыбы. Тақырыпта параллель көшіру туралы түсінік былай басталады. Жазықтық бетіне декарттық координаттар х пен у-ті енгізейік. F фигурасын, оның кез келген (х, у) нуктесі (х+a, у+b) нуктесіне көшетіндей етіп, а мен b - турақты шамалар, түлрендіруді параллель көшіру деп атайды.
Параллель көшіруді мынадай формулалармен көрсетіп береді:
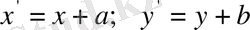
Бұл формулалар параллель көшіргенде (х, у) нүктесі ауысатын нүктенің х' пен у' координаттарын өрнектейді деп анықтама беру үшін осындай шұбалаңқы сөйлемдермен тұжырымдаған. Оқушыларға жоғарыдағыдай түсінік берсек олардың көкейіне қонбайтыны да белгілі, себебі беріліп тұрған анықтама оқушылардың басым көпшілігінің сана сезіміне негізделмеген. Сондықтан анықтама бермес бұрын координаттық жүйені енгізіп, одан координаттары (х, у) және (х', у') болатын М және N -нүктесін белгілеу керек. Осы екі нүктенің х осіндегі және у осіндегі сәйкесінше аралық санда а және b болсын деп келісілді.
Анықтама: Жазықтықтың кез-келген М(х, у) нүктесін N(х+a, у+b) нүктесіне көшіретіндей түрлендіруді параллель көшіру дейміз. . [13, 26]
Жоғарыдағы түрлендірумен Ғ фигурасының кез-келген нүктесін Ғ 1 фигурасының кез-келген нүктесіне параллель көшіруге болады. Олай болса Ғ фигурасын тұтастай Ғ 1 фигурасына параллель көшіруге болады.
Қысқаша былай жазамыз:
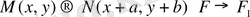 .
.
Енді параллель көшірудің қасиеттеріне тоқталайық.
1°. Параллель көшіру дегеніміз козғалыс болады. Мұны дәлелдеу ұшін төмендегі 1-сызбаны пайдаланамыз.
Қозғалыс болу үшін М және N нүктесінің арақашықтығы М 1 және N 1 нүктелерінің арақашықтығына тең бөлу керек, соны тексереміз.
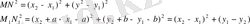 бұдан МN= М
1
N
1
олай болса параллель көшіру қозғалыс болғаны.
бұдан МN= М
1
N
1
олай болса параллель көшіру қозғалыс болғаны.
2°. Параллель көшіргенде нүктелер параллель (не беттесетін) түзулер бойымен бірдей қашықтыққа жылжиды.
Жоғарыдағы 1-сызбаны пайдаланып NМ
1
- кесіндісінің ортасын табайық, сонда
 нүктесінің координаттары мынадай болады:
нүктесінің координаттары мынадай болады:
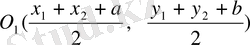
Енді МN
1
кесіндінің ортасын табайық, сонда
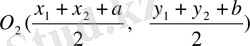 яғни, О
1
және О
2
нүктелерінің координаттары бірдей, бұл екі нүкте бір ғана О нүктесін айкындайды деген сөз.
яғни, О
1
және О
2
нүктелерінің координаттары бірдей, бұл екі нүкте бір ғана О нүктесін айкындайды деген сөз.
8-сыныпта өтілген параллелограмм туралы теорема бойынша
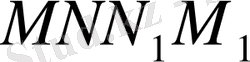 төртбұрышы параллелограмм. Параллелограмның анықтамасы және параллелограмның қарама-қарсы қабырғалары тең деген теорема бойынша.
төртбұрышы параллелограмм. Параллелограмның анықтамасы және параллелограмның қарама-қарсы қабырғалары тең деген теорема бойынша.
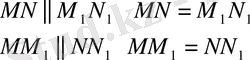
Егер N нүктесі ММ
1
түзуінде жатса. онда
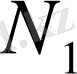 нүк-тесі де ММ
1
түзуінде жатады. Себебі
нүк-тесі де ММ
1
түзуінде жатады. Себебі
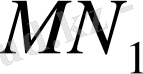 , кесіндісінің ортасы
, кесіндісінің ортасы
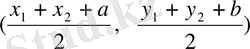 NМ
1
кесіндісінің ортасымен
NМ
1
кесіндісінің ортасымен
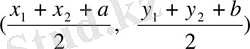 дәлме -дәл беттеседы, бұдан М, N, М
1,
N
1
нүктелері бір түзудің бойында жататындығы шығады, ал
дәлме -дәл беттеседы, бұдан М, N, М
1,
N
1
нүктелері бір түзудің бойында жататындығы шығады, ал
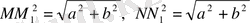 М және N нүктелері МN түзуінің бойымен
М және N нүктелері МN түзуінің бойымен
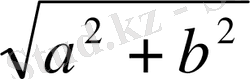 қашықтыққа жылжиды. Сонымен бұл дәлелдеулерден мына сандар шығады:
қашықтыққа жылжиды. Сонымен бұл дәлелдеулерден мына сандар шығады:
Параллель көшіргенде түзу параллель түзуге (не өзіне) көшеді.
Енді мына төмендегі теореманы дәлелдеу әдісіне көңіл бөлейік.
Теорема: М және М 1 екі нүкте қандай болса да М нүктесін М 1 нүктесіне көшіретіндей параллель көшіру бар болады және ол тек біреу ғана болады.
Алдымен 1-сызбаны пайдалана отырып, ондай көшіру жолының бірден-біреу ғана екенін дәлелдейміз.
Айталық N
1
нүктесі N нүктесі параллель көшіргенде оның көшетін нүктесі болсын. Өзіміз білетіндей
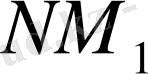 мен
мен
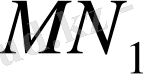 кесінділерінің орта нүктелері О ортақ. N нүктесін көрсетіп берудің өзі
кесінділерінің орта нүктелері О ортақ. N нүктесін көрсетіп берудің өзі
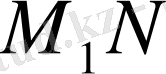 кесіндісінің ортасы - О нүктесін бір мәнді анықтайды. Ал М мен О нүктелері N
1
нүктесін бір мәнді анықтайды, өйткені О нүктесі
кесіндісінің ортасы - О нүктесін бір мәнді анықтайды. Ал М мен О нүктелері N
1
нүктесін бір мәнді анықтайды, өйткені О нүктесі
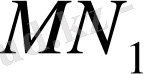 кесіндісінің ортасы болып табылады.
кесіндісінің ортасы болып табылады.
N 1 нүктесін анықтаудағы бір мәнділік деген сол параллель көшірудің бірден-біреу екендігін білдіреді. Енді М нүктесін М 1 нүктесіне көшіретін параллель көшірудің бар болатындығын дәлелдейік.
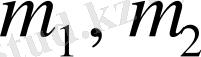 - М нүктесінің
- М нүктесінің
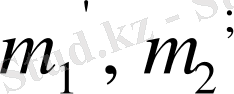 - М. нүктесінің координаттары болсын, сонда 3-сызба бойынша
- М. нүктесінің координаттары болсын, сонда 3-сызба бойынша
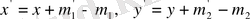 екіншіден
екіншіден
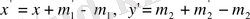
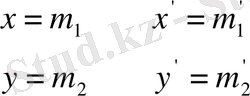
бұл М нүктесі М
1
нүктесіне мына формуламен
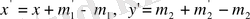 параллель көшті деген сөз, яғни М нүктесін М
1
нүктесіне көшіретін параллель көшіру бар екен.
параллель көшті деген сөз, яғни М нүктесін М
1
нүктесіне көшіретін параллель көшіру бар екен.
Айта кетер жайт параллель көшірудің анықтамасын беру мен қасиеттерін дәлелдеуге және есептер шығаруға 1 сағ. қалған екі теореманы дәлелдеуге және есеп шығаруға 1 сағ, сонымен бірге өтілгенді қорытындылауға және есептер шығаруға 1 сағ. уқыт бөлген дұрыс қой деп есептеймін.
Теорема: Параллель көшіруге кері саналатын түрлендіру параллель көшіру болады.
Бірінен кейін екіншісі орындалатын параллель екі көшіру тағы да параллель көшіру болады.
Оқушыларға белгілі бір дәрежеде параллель көшіру туралы ұғым берілгендіктен жоғарыдағы теоремалардың дәлелдемесін оқушылардың ойлау қабілетіне негіздеп дәлелдеп көрсеткен жеткілікті.
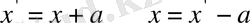
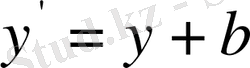 шынында да
шынында да
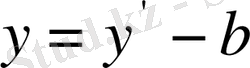

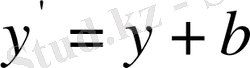
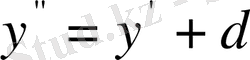 болса, онда
болса, онда
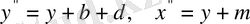
мұндағы
 сандар.
сандар.
Параллель көшіру такырыбына есептер шығарғанда жалаң шығармай, оны координат жазыктығында көрсетіп отыру аса пайдалы, себебі векторлар туралы өткен кезде оның пайдасы өзінен-өзі көрініс береді. Енді есеп шығарудың бірнеше үлгісін көрсете кету артық болмас деп ойлаймын.
Есеп: Параллель көшіру мына формулалармен
 көрсетіп беріледі. Осы параллель көшіруде (0, 0), (1, 0), (0, 2) нүктелері қандай нүктелерге көшеді?
көрсетіп беріледі. Осы параллель көшіруде (0, 0), (1, 0), (0, 2) нүктелері қандай нүктелерге көшеді?
Берілгені:

т/к (0, 0) -?
(1, 0) -?
(0, 2) -?
Шешуі:
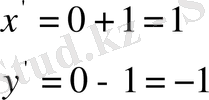
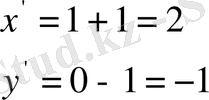
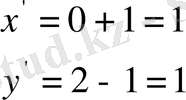
Яғни
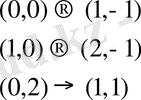
мұны координат жазықтығында көрсетейік. Есеп: Мынадай паралель көшіру
 формулаларындағы а мен b шамаларын табыңдар, сонда (1, 2) нүктесі (3, 4) нүктесіне көшетіндігі белгілі.
формулаларындағы а мен b шамаларын табыңдар, сонда (1, 2) нүктесі (3, 4) нүктесіне көшетіндігі белгілі.
Берілгені:

(1, 2) → (3, 4)
Т/к: а, b-?
Шешуі: 1+а=3, а=2
2 +b = 4, b =2.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz