Айнымалы токтардың тарихы мен теориясы: периодты токтар, синусоидалы шамалар және векторлы кескіндеу


Айнымалы токтар
1. Айнымалы тоқты пайдалануды ең алғаш рет 1875 жылы орыс ғалымы П. Н. Яблочков ұсынды. Айнымалы тоқ Яблочков шырағындағы өмірдің біркелкі жануын қамтамасыз етті және шамдардың бір электр энергия көзінен қоректенуге жол ашты.
Электр энергиясының қажеттілігінің өсуіне байланысты оны алыс қашықтықтарға жеткізу мәселесі алға қойылды. Бұл мәселенің шешілуі электр энергиясын таратуды, электр энергиясын алыс қашықтықтарға жеткізудегі тимдісі жоғары кернеу, ал қабылдағыштарға беру кезінде қауыпсіздік ережелерін сақтау үшін төмендегі кернеу қажет болды.
Кернеуді бұлай түрлендіру үшін айнымалы тоқты түрлендіретін құрлысы қарапайым трансформаторлар қажет болды, оны да өзінің шырақтары үшін Яблокович ойлап тапты.
Одан кейін атақты орыс инжинері және ғалымы М. О. Доливо -Добровольскийдің басшылығымен үш фазалы жүйе ойлап шығарылды М. О. Доливо-Доброволскийдің арқасында айнымалы тоқ кеңінен таралды 1889 жылы ол бірінші рет үш фазалы қозғалтқыш және үш фазалы тізбектің барлық тетіктерін жасап шығарды 1891 жылы ол электр энергиясын үш фазалы тоқпен 175 км қашықтыққа жеткізүді іске асырды.
Айнымалы тоқты электр техника саласында кеңінен пайдалану шоғырланған (централизацияланған ) түрде электр энергиясын өндірүді, алыс қашықтыққа жеткізуді, оны таратуды және қабылдауды игерген кезеңнен басталды.
Айнымалы тоққа қатысты ұғымдармен танысайық.
Айнымалы тоқ деп уақытқа байланысты шамасы мен бағыты өзгеріп отыратын тоқты айтамыз.
Айнымалы тоқтың кез келген аз уақыт мезгіліндегі мәнін лездік тоқ деп айтады, оны і -әрпімен белгілейді.
Лездік тоқтың (і) зарядқа және уақытқа байланысты екндігі мына қатынастан көрінеді:
I=dg/dt
.
Халықаралық СИ жүйесі бойынша тоқ күшінің бірлігі ретінде ампер (А) алынған. Бұл жүйеде заряд ампер-секундпен немесе кулонмен өлшенеді . 1 кулон (Кл) заряд 6, 29*10 18 электронның зарядына тең. Егер тоқ күші 1 ампер болса, онда өткізгіштің көлденең қимасы арқылы секундына 6, 29*10 18 электрон ағып өтеді деген сөз.
Егер лездік тоқтың уақыты уақытқа тәуелдігі белгілі болса i=F(t) және оның бағыты көрсетілсе, онда тоқты белгілі деп есептеуге болады. Айнымалы тоқтардың формасы әр түрлі, соның ішінде көп тарағанының бірі периодты тоқтар.
Периодты тоқтар деп тоқтың лездік мәндері бірдей уақыт аралықтарында қйталанып отыратын ең аз уақыты сол тоқтың периоды деп аталады, оны Т әрпімен белгілейді. Периодты тоқ үшін:
i=F(t) =F(t+T)
2. 1- сурет Айнымалы тоқ графигі
2. 1-суретте электр тізбегінің АВ бөлігі көрсетілген және периодты ток үшін мысал ретінде токтың уақытқа тәуелділігі көрсетілген i=F(t) . Схемадағы стрелка токтың оң бағытын көрсетеді. Үзік сызықты стрелкамен i>0 және i<0 болған кездердегі токтың нақты бағыттары көрсетілген.
Қисық сызық бойындағы кесінділер «а» мен «в», «о» және «с» аралықтарын токтың бір период кезіндегі толық циклі дейміз.
Периодқа кері шаманы жиілік дейміз, ол ν өрнегімен белгіленеді және герцпен (Гц) өлшенеді.
ν=1/ Т (Гц) (2. 3)
Электр- техникада қолданылатын айнымалы токтардың жиілік диапазон өте кең. Ол ондаған герцтен миллиард герцке дейін барады. СССР және Европа электр энергетикасында стандарт жиілік тағайындалған (өндірістік 50 Гц, ал АҚШ пен Жапонияда 60 Гц) .
Жоғарыда сөз болған және жаңадан енгізілген анықтамалардың барлығы бұдан былай да кернеу, ЭҚК-і, магнит ағымдары үшін пайдаланыла береді. Кернеу және ЭҚК-і жайында сөз еткенде, схемада олардың оң бағытын стрелкамен немесе әріптің төмен жағына қойылған индекс арқылы белгілеу қажет.
Электр энергиясында қарапайым гармониялық немесе синусоидалы тоқтарды пайдаланылады, яғни токтың уақытқа тәуелділігі синусоидалы функция болады. Радиотехникада, автоматикада, телемеханикада және есептеу техникасында синусоидалы емес периодты токтарды пайдаланған кезде біраз қиындықтарға кездесеміз. Олар: электр энергиясының шығынын ұлғаюы, тізбектің кейбір бөліктерінде едәуір кернеудің пайда болуы, электр байланыстарының (телеграф, телефон) жұмыстарына кедергі келтіретін бұрмалаушы жағдайлардың тууы.
Синусоидалы емес периодты токтар дегеніміз әр түрлі жиіліктегі синусоидалы токтардың жиынтығы.
Электр тізбектерінің осы құбылыстары бізге синусоидалы токтарды түбірлі зерттеп білуді талап етеді.
2 Синусоидал ЭҚК-ті, кернеуді және тоқты вектормен кескіндеу.
Синусоидал шамаларды тікбұрышты координаттар жазықтығында тұрғызу, оларды графикалық қосу және алу біршама қиын жұмыс. Егер оларды вектормен кескіндесе бұл жұмыс онайланған болар еді. Енді сиусоидал шамаларды вектор арқылы кескіндеуге болатының көрсетелік.
ОХ және ОУ кординат белдіктері (осьтері) жазықтығында ω тұрақты бұрыштық жиілікпен (жылдамдықпен) ОА векторы О нүктесінең айналып тұр делік. Вектордың ұзындығы сиусоидал ЭҚК-тің амплитудасына тең болсын, яғни
ОА=Е т
Айналудың оң бағыты үшін сағат тілінің айналу бағытына қарсы бағытты алалық, ал айналу бұрышын ОХ осінен бастап есептелік.
Көршілес координаттар жазықтығында (OX және ωt осьтері бір горизонталь түзудің бойнда жатуы керек) вектордың ОУ осіне проекциясының айналу бұрышынан тәулділігін тұрғызалық (2. 7-сурет) .
Басында ( t=0 ) ОА векторы ОХ осімен бағытталған делік. . Онда оның ОУ осіне проекциясы нөлге тең (е о нүктесі) . t 1 уақыт өткенен кейін вектор ωt 1 бұршына бұрылады да, оның ОУ осіне проекциясы
ОА 1 =ОА sin ωt 1 = E m sinωt 1 =e 1
t 1 уақыттан кейін вектор ωt 2 бұрышына бұрылады, ал оның ОУ осіне проекциясы ОА 2 =ОА sin ω t 2 =E m sin ω t 2 =e 2 болады.
Міне осылайша жалғастыра берсе
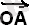 векторы координаттар басынан толық бір айналып шыққанда
ОУ
осіне проекциясы айналу бұрышына байланысты толық синусойда сызып шығады. Бұл факт синусойдал шаманы, біздің мысалда ЭҚК, сағат тілінің бағытына қарсы, ұзындығы синусойдал шаманың амплитудасына тең, ал бұрыштық жылдамдығы бұрыштық жиілікке тең айналып тұрған вектормен кескіндеуге болатындығын көрсетеді.
векторы координаттар басынан толық бір айналып шыққанда
ОУ
осіне проекциясы айналу бұрышына байланысты толық синусойда сызып шығады. Бұл факт синусойдал шаманы, біздің мысалда ЭҚК, сағат тілінің бағытына қарсы, ұзындығы синусойдал шаманың амплитудасына тең, ал бұрыштық жылдамдығы бұрыштық жиілікке тең айналып тұрған вектормен кескіндеуге болатындығын көрсетеді.
Егер вектордың бастапқы орны ОХ осімен сәйкес келмесе, онда синусойда координаттар басынан өтпейді - оның бастапқы фазасы болады. (2, 8 - сурет) .
Мысалы, е 1 ЭҚК-нің бастапқы фазасы φ 1 де, е 2 ЭҚК-нің бастапқы фазасы - φ 2 . Фазалар ығысуы φ=φ 1 -(-φ 2 ) =φ 1 +φ 2 .
Синусойдал шамаларды координаттар жазықтығында айналмалы вектор арқылы кескіндегенде бұрыштың сан мәнің ОХ осінен бастап есептеуге келісілген. Мұнда сағат тілінің бағытына қарсы бағытта саналған бұрыш плюс таңбасымен, ал сағат тілінің бағытымен саналған бұрыш минус таңбасымен алынады.
2, 9-суретте вектормен кескінделген екі синусойдал ЭҚК - ті қосу көрсетілген:
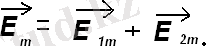
Мұнда екі синусойдал шаманың қосындысы вектормен кескінделген үшінші синусойдал шама е=E m sin(ωt+φ) болады.
Есептің қойылымы:
Берілгені:
Е2=2в; Е3=12в; Е4=15; Е5=15в; Е7=20в;
J1=10A; R7=1oм; R3=3ом; R5=5ом; R6=10ом; R8=2. 3ом;
Кіріспе
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz