Механиканың физикалық негіздері: кинематика және қозғалыстың сипаттамалары


Тақырып: Механиканың физикалық негіздері
Кинематика негіздері
Кинематика - дене қозғалысын қамтамасыз ететін себептерге байланыссыз қозғалысты оқып зерттейді, статика - денелердің тепе-теңдіктегі шартын зерттейді, ал динамика -қозғалыстың сол немесе басқадай сипатын қамтамасыз ететін себептерге байланысты денелердің қозғалысын оқып зерттейді.
Уақыт өтуіне байланысты денелердің кеңістікте орын ауыстыруын механикада қозғалыс деп атайды.
Механикалық қозғалыстың ең қарапайым мысалы ретінде материалық нүкте қозғалысын қарастыруға болады. Материалдық нүкте деп массасы қарастырылып отырған дененің массасына тең, берілген есептің шартында өлшемін елемеуге болатын денені айтады.
Материалдық нүкте орнын қандай-да бір болмасын кез-келген денеге, яғни санақ денесіне қатысты анықтауға болады. Кез-келген таңдап алынған нүкте тыныштықта тұр деп аламыз, ал соған қатысты кез-келген координат жүйесін кеңістіктік санақ жүйесі деп атайды. Кеңістіктік санақ жүйесіндегі әрбір нүктенің орны
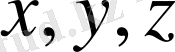 координаттарымен анықталады. Осы үш координаттың орнына
координаттарымен анықталады. Осы үш координаттың орнына
 радиус-векторды алуға болады. Радиус-вектор деп координаттар басынан қарастырылып отырған нүктеге дейін бағытталған кесіндіні айтады. Қозғалысты сипаттау үшін кеңістіктік санақ жүйесі жеткіліксіз болып саналады. Қозғалысты тек кеңістік -уақыт санақ жүйесінде ғана толық сипаттауға болады. Уақыт өзгерісіне байланысты материалдық нүкте қозғалысы мына теңдеумен беріледі:
радиус-векторды алуға болады. Радиус-вектор деп координаттар басынан қарастырылып отырған нүктеге дейін бағытталған кесіндіні айтады. Қозғалысты сипаттау үшін кеңістіктік санақ жүйесі жеткіліксіз болып саналады. Қозғалысты тек кеңістік -уақыт санақ жүйесінде ғана толық сипаттауға болады. Уақыт өзгерісіне байланысты материалдық нүкте қозғалысы мына теңдеумен беріледі:
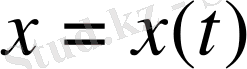
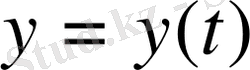 (1. 1)
(1. 1)
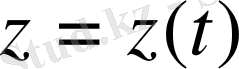
және
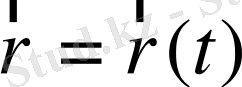 (1. 2)
(1. 2)
(1. 1) және (1. 2) теңдеулері материалдық нүктенің кинематикалық теңдеулері деп аталады.
Материялдық нүктенің қозғалысы кезінде із қалдыруын оның траекориясы деп атайды. Траекторияның формасына қарай түзу сызықты және қисық сызықты деп екіге бөлуге болады. Материялдық нүкте қозғалысын траекториямен беттестіре сызсақ,
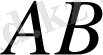 траектория ұзындығын материялдық нүктенің жүрген жолы деп атайды. Оны
траектория ұзындығын материялдық нүктенің жүрген жолы деп атайды. Оны
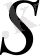 әрпімен белгілейді, жүрілген жол скаляр шама
әрпімен белгілейді, жүрілген жол скаляр шама

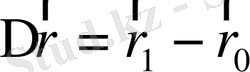 -бастапқы моменттен соңғы уақыт мезетіне дейінгі ара қашықтық
-бастапқы моменттен соңғы уақыт мезетіне дейінгі ара қашықтық
 ,
орын ауыстыру
деп аталады. Ол - векторлық шама. Егер
траектория түзу сызықты болса, онда жүрілген жол мен орын ауыстыру
беттеседі.
Дене түзу бойымен қозғалса, қозғалыс түзу сызықты деп
аталады.
Егер қозғалған дене кез-келген өзара тең уақыт аралығында бірдей жол жүрсе, ондай қозғалысты бірқалыпты түзу сызықты қозғалыс деп атайды. Қозғалыс түрліше болуы мүмкін, мысалы әр түрлі дене бірдей уақыт аралығында әр түрлі жол жүреді, қозғалыстың осындай өзгерісін біз
,
орын ауыстыру
деп аталады. Ол - векторлық шама. Егер
траектория түзу сызықты болса, онда жүрілген жол мен орын ауыстыру
беттеседі.
Дене түзу бойымен қозғалса, қозғалыс түзу сызықты деп
аталады.
Егер қозғалған дене кез-келген өзара тең уақыт аралығында бірдей жол жүрсе, ондай қозғалысты бірқалыпты түзу сызықты қозғалыс деп атайды. Қозғалыс түрліше болуы мүмкін, мысалы әр түрлі дене бірдей уақыт аралығында әр түрлі жол жүреді, қозғалыстың осындай өзгерісін біз
 жылдамдық деген ұғым енгізу арқылы сипаттаймыз. Жылдамдық-векторлық шама, ол траекторияға жүргізілген жанама бойымен бағытталады. Қозғалыстың жылдамдығы жүрілген жолға тура пропорционал, сол жолды жүруге кеткен уақытқа кері пропорционал:
жылдамдық деген ұғым енгізу арқылы сипаттаймыз. Жылдамдық-векторлық шама, ол траекторияға жүргізілген жанама бойымен бағытталады. Қозғалыстың жылдамдығы жүрілген жолға тура пропорционал, сол жолды жүруге кеткен уақытқа кері пропорционал:
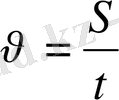 , өлшем бірлігі
, өлшем бірлігі
 .
.
Біқалыпсыз қисық сызықты қозғалыс. Айнымалы қозғалыс кезінде бірдей уақыт аралығында материалдық нүктенің жүрген жолдары бірдей болмайды. Мұндай жағдайда қозғалыстың орташа жылдамдығы деген ұғым енгізуіміз керек. Орташа жылдамдық векторы деп нүктенің радиус векторының өсімшесінің осы уақыт аралығына қатынасын айтамыз:
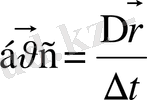 (1. 3)
(1. 3)
Материалдық нүктенің берілген уақыт мезетіндегі қозғалысын лездік жылдамдық арқылы сипаттайды. Лездік жылдамдық
 уақыт аралығы шексіз кемігендегі орташа жылдамдық ұмтылатын шекке тең:
уақыт аралығы шексіз кемігендегі орташа жылдамдық ұмтылатын шекке тең:
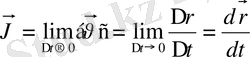 (1. 3а)
(1. 3а)
Жылдамдық деп орын ауыстыру векторының уақыт бойынша алынған туындысына тең және траекторияға берілге нүктеге жүргізілген жанамамен бағыттас векторды айтады.
 уақыт аралығы азайған сайын
уақыт аралығы азайған сайын
 жүрілген жолы
жүрілген жолы
 орын ауыстыруға жақындап беттеседі.
орын ауыстыруға жақындап беттеседі.
Сонда уақыттың кез-келген мезетіндегі қозғалыс жылдамдығы деп, жүрілген жолдың уақыт бойынша алынған бірінші ретті туындысын айтамыз.
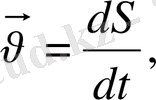 (1. 4)
(1. 4)
бұдан
 .
.
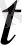 - дан
- дан
 шектерінде интегралдап жүрілген жолдың ұзындығын анықтаймыз :
шектерінде интегралдап жүрілген жолдың ұзындығын анықтаймыз :
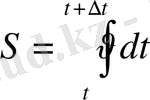 (1. 4а)
(1. 4а)
Бірқалыпсыз қозғалыс кезінде біз уақыт өтуіне байланысты жылдамдықтың қалай өзгеретіндігін қарастырамыз. Егер қозғалыс жылдамдығы ұдайы артып отырса, үдемелі қозғалыс деп, егер жылдамдығы ұдайы кеміп отырса, онда кемімелі қозғалыс деп атайды. Олай болса уақытқа байланысты жылдамдықтың қаншалықты тез өзгеретіндігін сипаттайтын үдеу деген физикалық шаманы енгіземіз. Бірқалыпсыз қозғалыстың үдеуі дегеніміз жылдамдықтың өсімшесіне тура пропорционал және осы өсімше пайда болған уақыт өсімшесіне кері пропорционал шама:
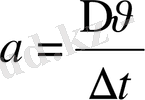 .
.
Бұл жағдайда қозғалыс айнымалы болғандықтан жылдамдық өсімшесінің өзгеруіне сәйкес үдеу де өзгерісте болады, олай болса орташа үдеу деген ұғым енгізуге тура келеді:
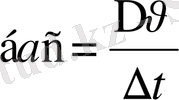 . Орташа үдеу алынып отырған
. Орташа үдеу алынып отырған
 уақыт аралығы шексіз кемігенде, сол орташа үдеудің ұмтылатын шегін лездік үдеу деп атайды.
уақыт аралығы шексіз кемігенде, сол орташа үдеудің ұмтылатын шегін лездік үдеу деп атайды.
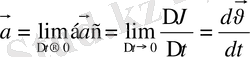 .
.
Демек, үдеу шама жағынан жылдамдықтың уақыт бойынша алынған бірінші ретті туындысы, ал жүрілген жолдың уақыт бойынша алынған екінші ретті туындысына тең:
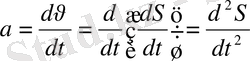 (1. 5)
(1. 5)
Үдеу қозғалыс жылдамдығын саны жағынан да, бағыты жағынан да сипаттайды. Сондықтан ол векторлық шама, өлшем бірлігі:
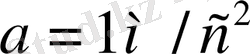 . Бастапқы уақыт мезетінде қозғалыс жылдамдығы
. Бастапқы уақыт мезетінде қозғалыс жылдамдығы
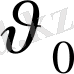 , ал
, ал
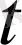 уақыттан кейін
уақыттан кейін
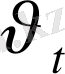 болсын, онда қозғалыс үдеуі
болсын, онда қозғалыс үдеуі
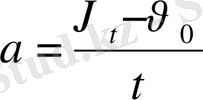 болады. Қозғалыстың кез-келген уақыт мезетіндегі жылдамдығы:
болады. Қозғалыстың кез-келген уақыт мезетіндегі жылдамдығы:
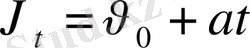 . Олай болса бірқалыпты айнымалы қозғалыс теңдеуін шығарып алуға болады:
. Олай болса бірқалыпты айнымалы қозғалыс теңдеуін шығарып алуға болады:
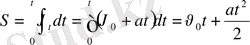 , яғни
, яғни
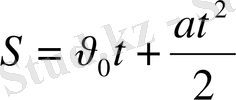 (1. 6)
(1. 6)
Дененің қисық сызық бойымен қозғалысын қарастырайық. Бастапқы
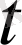 уақыт мезетіеде
уақыт мезетіеде
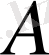 нүктесінің жылдамдығы
нүктесінің жылдамдығы
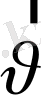 болсын. Қозғалыстағы нүкте
болсын. Қозғалыстағы нүкте
 уақытта
уақытта
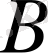 нүктесіне көшіп,
нүктесіне көшіп,
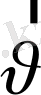 жылдамдығынан бағыты жағынан да, модулы жағынан да өзгеше
жылдамдығынан бағыты жағынан да, модулы жағынан да өзгеше
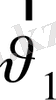 жылдамдыққа ие болады:
жылдамдыққа ие болады:
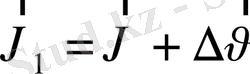 . Енді
. Енді
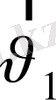 векторын
векторын
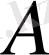 нүктесіне көшіріп,
нүктесіне көшіріп,
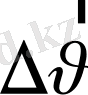 табамыз.
табамыз.
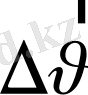 векторын екі құраушыға жіктеуге болады. Ол үшін
векторын екі құраушыға жіктеуге болады. Ол үшін
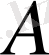 нүктесінен жылдамдық бағытымен бағыттас, модулы жағынан
нүктесінен жылдамдық бағытымен бағыттас, модулы жағынан
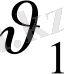 векторына тең
векторына тең
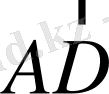 векторын жүргіземіз. Бұдан
векторын жүргіземіз. Бұдан
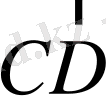 векторы шамасы жағынан
векторы шамасы жағынан
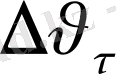 -ға тең,
-ға тең,
 уақыт аралығында жылдамдық өзгерісін модулы жағынан сипаттайды:
уақыт аралығында жылдамдық өзгерісін модулы жағынан сипаттайды:
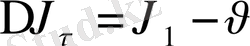 . Екінші құраушы вектор
. Екінші құраушы вектор
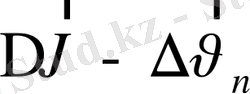 ,
,
 уақыт аралығында жылдамдық өзгерісін бағыты жағынан сипаттайды.
уақыт аралығында жылдамдық өзгерісін бағыты жағынан сипаттайды.
Үдеудің тангенциал құраушысы
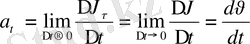 (1. 7)
(1. 7)
яғни жылдамдық модулынан уақыт бойынша алынған бірінші ретті туындыға тең, жанамаға бағыттас жылдамдықтың өзгеріс шапшаңдығын модулы жағынан сипаттайды. Енді үдеудің екінші құраушысын табайық.
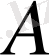 нүктесі
нүктесі
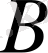 нүктесіне орын ауыстырып,
нүктесіне орын ауыстырып,
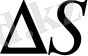 доғасына тең элементар жол жүреді.
доғасына тең элементар жол жүреді.
 уақыт аралығы өте аз болғандықтан
уақыт аралығы өте аз болғандықтан
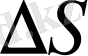 доғасының
доғасының
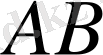 хордасынан айырмашылығы аз болады. Онда
хордасынан айырмашылығы аз болады. Онда
 және
және
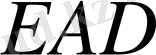 үшбұрыштарының ұқсастығынан
үшбұрыштарының ұқсастығынан
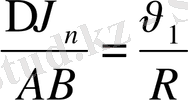 шығады. Ал
шығады. Ал
 , онда
, онда
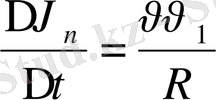 .
.
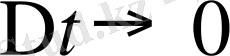 шегінен,
шегінен,
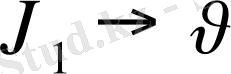 аламыз.
аламыз.
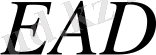 бұрышы нольге ұмтылады, себебі
бұрышы нольге ұмтылады, себебі
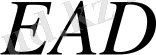 үшбұрышы тең қабырғалы.
үшбұрышы тең қабырғалы.
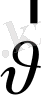 мен
мен
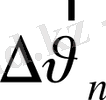 векторының арасындағы
векторының арасындағы
 бұрышы тік бұрышқа ұмтылады. Бұдан
бұрышы тік бұрышқа ұмтылады. Бұдан
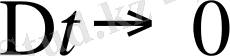 ,
,
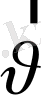 және
және
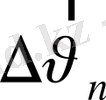 векторлары өзара перпендикуляр болады. Жылдамдық векторы
векторлары өзара перпендикуляр болады. Жылдамдық векторы
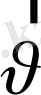 қозғалыс траекториясына жанамаға бағытталғандықтан,
қозғалыс траекториясына жанамаға бағытталғандықтан,
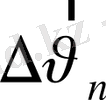 векторы жанамаға перпендикуляр бағытталады да, жылдамдықтың бағыты бойынша өзгерісін сипаттайды. Үдеудің екінші құраушысы
векторы жанамаға перпендикуляр бағытталады да, жылдамдықтың бағыты бойынша өзгерісін сипаттайды. Үдеудің екінші құраушысы
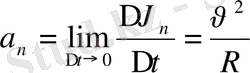 , (1. 8)
, (1. 8)
үдеудің нормаль құраушысы деп аталады және қозғалыс траекториясының радиус бойымен центріне бағытталады (сондықтан оны центрге тартқыш үдеу деп те атаймыз) .
Дененің толық үдеуі тангенциаль және нормаль құраушылардың геометриялық қосындысынан тұрады, яғни
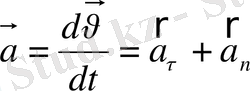
Толық үдеудің модулы мынаған тең:
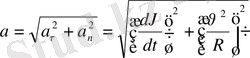 (1. 9)
(1. 9)
Тангенциал және нормаль құраушыларына байланысты үдеудің қозғалысын былай сипаттауға болады:
1.
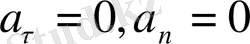 - бірқалыпты түзу сызықты қозғалыс,
- бірқалыпты түзу сызықты қозғалыс,
2.
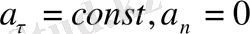 - бірқалыпты айнымалы қозғалыс,
- бірқалыпты айнымалы қозғалыс,
3.
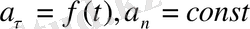 - үдеуі айнымалы түзу сызықты қозғалыс,
- үдеуі айнымалы түзу сызықты қозғалыс,
4.
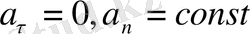 - шеңбер бойымен қозғалыс,
- шеңбер бойымен қозғалыс,
5.
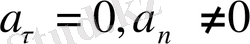 - бірқалыпты қисық сызықты қозғалыс,
- бірқалыпты қисық сызықты қозғалыс,
6.
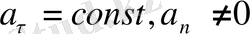 - қисық сызықты айнымалы қозғалыс,
- қисық сызықты айнымалы қозғалыс,
7.
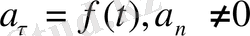 -үдеуі айнымалы қисық сызықты қозғалыс.
-үдеуі айнымалы қисық сызықты қозғалыс.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz