Арнайы салыстырмалық теориясының элементтері: Галилей және Лоренц түрлендірулері, релятивистік динамика мен масса-энергия қатынасы


Салыстырмалық теориясының элементтері
Лекцияның жоспары:
1. Галилей түрлендірулері
2. Эйнштейн постулаттары
3. Лоренц түрлендірулері
4. Лоренцше түрлендірудің кейбір салдарлары
5. Жылдамдықтарды қосу теоремасы
6. Материалдық нүктенің релятивистік динамикасының негізгі заңы
7. Масса және энергияның өзара байланыс заңы
1. Галилей түрлендірулері
Егер санақ жүйелері бір-бірімен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалса және олардың біреуінде Ньютонның динамика заңдары орындалатын болса, онда бұл жүйелер инерциалдық санық жүйелері болып табылады. Барлық инерциалдық санақ жүйелерінде классикалық динамика заңдары бірдей формада болады, салыстырмалы принципінің негізі осында (Галилейдің салыстырмалы принципі) . Дәлелдеу үшін 2 санақ жүйесін қарастырайық: қозғалмайтын инерциалдық жүйе
К
(координаттары
х, у, z
) және
К
жүйесіне қатысты түзу сызықтың бойымен бірқалыпты
 (
(
 ) жылдамдықпен қозғалатын
) жылдамдықпен қозғалатын
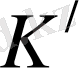 жүйесі. Бастапқы
жүйесі. Бастапқы
 мезетте екі жүйенің координаталарының бастары дәлме-дәл келіп тұрған болсын. Кез-келген
мезетте екі жүйенің координаталарының бастары дәлме-дәл келіп тұрған болсын. Кез-келген
 уақыт мезетіндегі бұл жүйелердің бір-біріне қатысты орналасуы суретте көрсетілгендей болсын. Жылдамдық
уақыт мезетіндегі бұл жүйелердің бір-біріне қатысты орналасуы суретте көрсетілгендей болсын. Жылдамдық
 ОО
ОО
 -
дің бойымен бағытталсын,
О
-дан
О
-
дің бойымен бағытталсын,
О
-дан
О
 -
не жүргізілген радиус-вектор
-
не жүргізілген радиус-вектор
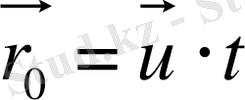 . Екі жүйедегі
. Екі жүйедегі
 нүктесінің координаталарының өзара байланыстын табамыз. 1-суреттен
нүктесінің координаталарының өзара байланыстын табамыз. 1-суреттен
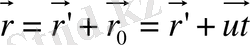
1-сурет.
Бұл теңдеуді координаталар осіне проекциялары арқылы жазуға болады.
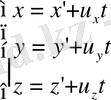 (1)
(1)
бұл теңдеулерді Галилей түрлендірулері деп атайды .
Дененің бір инерциалдық санақ жүйесіндегі координаталары мен ол жүйемен салыстырғанда бір қалыпты және түзу сызықты қозғалыстағы екінші инерциалдық жүйедегі координаталарын байланыстыратын қатынастарды Галилей түрлендірулері деп атайды.
Егер
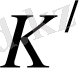 жүйесі
К
жүйесіне қатысты
жүйесі
К
жүйесіне қатысты
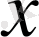 осі бойымен
осі бойымен
 жылдамдықпен қозғалатын болса (бастапқы уақыт мезетінде координаталар осі беттессін), онда координаталарды
Галилейше түрлендіру мына түрде жазылады:
жылдамдықпен қозғалатын болса (бастапқы уақыт мезетінде координаталар осі беттессін), онда координаталарды
Галилейше түрлендіру мына түрде жазылады:
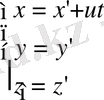
 (2)
(2)
Классикалық механикада уақыт санақ жүйелерінің салыстырмалы қозғалысына тәуелсіз, сондықтан жоғарыдағы түрлендіруге тағы да бір теңдеу қосуға болады:
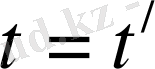 (3)
(3)
Жазылған қатынастардың бәрі тек қана классикалық механика (
 ) тұрғысынан қарағанда орындалады, ал жарық жылдамдығына жақын жылдамдықтар үшін Галилей түрлендіруі жалпы Лоренц түрлендірулерімен алмастырылады.
) тұрғысынан қарағанда орындалады, ал жарық жылдамдығына жақын жылдамдықтар үшін Галилей түрлендіруі жалпы Лоренц түрлендірулерімен алмастырылады.
(1) -теңдеуді уақыт бойынша дифференциалдайтын болсақ, классикалық мехакниканың жылдамдықтарынан қосу заңын аламыз:
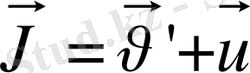 (4)
(4)
К
санақ жүйесінде үдеу
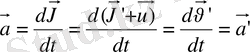
Сонымен, бір-бірімен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалатын
К
және
 жүйелерінде,
жүйелерінде,
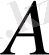 нүктесінің үдеуі бірдей болады:
нүктесінің үдеуі бірдей болады:
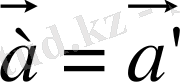 (5)
(5)
Демек, егер
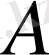 нүктесіне басқа денелер әсер етпейтін болса (
нүктесіне басқа денелер әсер етпейтін болса (
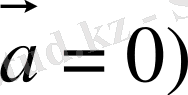 , онда берілген теңдеуге сәйкес
, онда берілген теңдеуге сәйкес
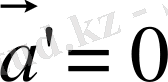 , яғни
, яғни
 жүйесі инерциалды (нүкте онымен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалады немесе тыныштық қалпын сақтайды) .
жүйесі инерциалды (нүкте онымен салыстырғанда түзу сызықтың бойымен бірқалыпты қозғалады немесе тыныштық қалпын сақтайды) .
(5) -теңдеуден салыстырмалықтың механикалық принципінің дәләлдемесі шығады; динамика заңдары бір инерциалдық санақ жүйесінен екіншісіне көшкенде өзгермейді, яғни координаталар түрлендірулеріне қатысты инвариантты болып табылады. Бұл Галилейдің қорытындысы.
2. Эйнштейн постулаттары
Арнайы салыстырмалы теорияның негізін тұжырымдаған Эйнштейн мынадай екі постулат ұсынды:
І постулат : берілген жүйенің тыныш тұрғандығын немесе тұрақты жылдамдықпен қозғалып бара жатқандығын сол жүйенің ішінде жасалған тәжірибе арқылы біліп болмайды. Басқаша айтқанда, қандай тәсілдер қолданғанымен абсолют қозғалысты анықтау мүмкін емес.
ІІ постулат : жарықтың вакуумдағы жылдамдығы барлық инерциялдық санақ жүйесінде бірдей және тұрақты шама болады. Басқаша айтқанда, жарық жылдамдығы жарық көзі мен бақылаушы қоғалысына тәуелді емес.
Эйнштейннің бірінші постулаты әдетте салыстырмалық принципі, ал екінші постулаты - жарық жылдамдығының тұрақтылық принципі деп аталады. Эйнштейннің осы теоремасы ХХ ғасырда өрбіген ең маңызды физикалық теориялардың бірі болып табылады.
3. Лоренц түрлендірулері
Эйнштейн постулаттарын негізге ала отырып, инерциалдық санақ жүйелеріндегі құбылыстарға талдау жасау арқылы классикалық Галилей түрлендірулерінің оларға қайшы екендігін және басқа түрлендірулермен ауыстырылуы тиістігін көрсетті.
Енді қысқаша соған тоқталайық. Екі инерциялық санақ жүйелерін қарастырайық:
К
(координаталары
х, у, z)
және
 жүйесіне қатысты
х
осі бойымен
жүйесіне қатысты
х
осі бойымен
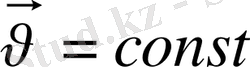 жылдамдықпен қозғалатын
К
жылдамдықпен қозғалатын
К
 (координаттары
x
(координаттары
x
 , y
, y
 , z
, z
 ) 1-сурет. Бастапқы
t=t
) 1-сурет. Бастапқы
t=t
 =0
уақыт мезетінде координаталардың бастары
О
және
О
=0
уақыт мезетінде координаталардың бастары
О
және
О
 бір-біріне дәл келсін, сонда жарық импульсі шығарылады.
бір-біріне дәл келсін, сонда жарық импульсі шығарылады.
1-сурет.
Эйнштейннің ІІ постулаты бойынша, екі жүйедегі жарық жылдамдығы бірдей және
с-
ға тең. Сондықтан егер
 уақытта
К
жүйесінде сигнал А нүктесіне дейін жеткенше,
уақытта
К
жүйесінде сигнал А нүктесіне дейін жеткенше,
 (6) арақашықтық жүрсе, онда
(6) арақашықтық жүрсе, онда
 жүйесінде жарық импульсі А нүктесіне жеткен мезетінде
жүйесінде жарық импульсі А нүктесіне жеткен мезетінде
 (7)
(7)
мұндағы
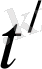 -жарық импульсінің
-жарық импульсінің
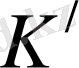 жүйесінде координаталар басынан А нүктесіне дейінгі жүрген уақыты. Теңдеулердің айырымынан мынаны аламыз:
жүйесінде координаталар басынан А нүктесіне дейінгі жүрген уақыты. Теңдеулердің айырымынан мынаны аламыз:
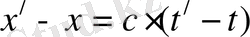 .
К
жүйесіне қатысты
.
К
жүйесіне қатысты
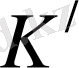 жүйесі орын ауыстырады. Сондықтан
жүйесі орын ауыстырады. Сондықтан
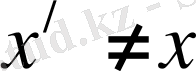 , онда
, онда
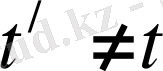 , Яғни
К
және
, Яғни
К
және
 жүйелеріндегі уақыт санауы әртүрлі - уақыт санағы салыстырмалы.
жүйелеріндегі уақыт санауы әртүрлі - уақыт санағы салыстырмалы.
Эйнштейн салыстырмалылы теориясында Галилейдің классикалық түрлендірулері, постулаттарды қанағаттандыратын Лоренц түрлендірулеріне ауыстырылатынын көрсетеді. Лоренц түрлендірулерін мына формулалар түрінде жазуға болады:


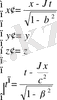
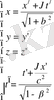 (8)
(8)
мұндағы
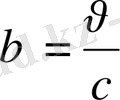
Келтірілген теңдеулер симметриялы және тек
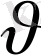 -ның алдындағы таңбамен ғана ажыратылады. Лоренц түрлендірулерін талдай келіп, мынадай қорытындылар жасауға болады:
-ның алдындағы таңбамен ғана ажыратылады. Лоренц түрлендірулерін талдай келіп, мынадай қорытындылар жасауға болады:
Егер
 болса, яғни
болса, яғни
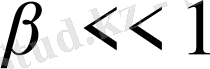 , онда Лоренцше түрлендірулер Галилейше түрлендіру формуласына айналады. Сөйтіп салыстырмалы жылдамдық жарықтың вакуумдағы жылдамдығынан кем болса ғана Галилейше түрлендіруде мағына бар. Егер
, онда Лоренцше түрлендірулер Галилейше түрлендіру формуласына айналады. Сөйтіп салыстырмалы жылдамдық жарықтың вакуумдағы жылдамдығынан кем болса ғана Галилейше түрлендіруде мағына бар. Егер
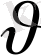 >c
болса, онда жоғардағы формулалар бойынша
>c
болса, онда жоғардағы формулалар бойынша
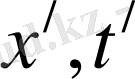 және
x, t
шамалары жалған шамалар болады. Бұл вакуумдағы жарық жылдамдығынан зор жылдамдықпен қозғалу мүмкін емес деген қағидаға сай келеді.
және
x, t
шамалары жалған шамалар болады. Бұл вакуумдағы жарық жылдамдығынан зор жылдамдықпен қозғалу мүмкін емес деген қағидаға сай келеді.
4. Лоренцше түрлендірудің кейбір салдарлары
Лоренцше түрлендіру формулаларынан маңызды бірнеше қорытындылар шығады. Енді солардың кейбіреулеріне тоқталайық.
Оқиғалардың бір мезгілдігі .
Мысалы,
К
жүйесінде координаталары
х
1
және
х
2
нүктелерінде
t
1
және
t
2
мезеттерде бір-бірден екі оқиға болған болсын.
К
/
жүйесінде сонда оларға
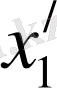 және
және
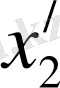 келеді. Егер олар
К
жүйесінде бір нүктеде (
х
1
= х
2
) және бір мезетте болса, сонда формулалар бойынша
келеді. Егер олар
К
жүйесінде бір нүктеде (
х
1
= х
2
) және бір мезетте болса, сонда формулалар бойынша
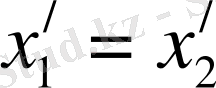 және
және
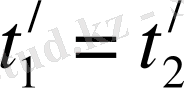 . Яғни, бұл құбылыстар кез-келген инерциалдық санақ жүйесінде де бір мезгілде бір орында (бір нүктеде) болады.
. Яғни, бұл құбылыстар кез-келген инерциалдық санақ жүйесінде де бір мезгілде бір орында (бір нүктеде) болады.
Ал, егер оқиға кеңістікте әр нүктеде х 1 ≠ х 2 , бірақ бір мезгілде t 1 = t 2 болса, онда (8) формулаларға сәйкес К / жүйеде Лоренц түрлендіруінше

Демек,
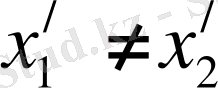 ,
,
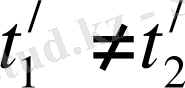
Сонымен бұл құбылыстар
 санақ жүйесінде бір мезгілде болмайды, кеңістіктегі орындары бөлек болады.
санақ жүйесінде бір мезгілде болмайды, кеңістіктегі орындары бөлек болады.
Түрліше жүйелердегі дене ұзындықтарын салыстыру
Бұрынғыша инерциялық
К
және
 санақ жүйелерін алайық.
санақ жүйелерін алайық.
 жүйесі
К
жүйесіне қатысты
жүйесі
К
жүйесіне қатысты
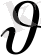 жылдамдықпен қозғалып бара жатсын. Сонда
х
осінің бойымен орналасқан бір қатты шыбықтың
К
жүйесіндегі ұзындығы
жылдамдықпен қозғалып бара жатсын. Сонда
х
осінің бойымен орналасқан бір қатты шыбықтың
К
жүйесіндегі ұзындығы
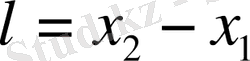 .
.
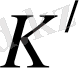 жүйесіндегі ұзындығы
жүйесіндегі ұзындығы
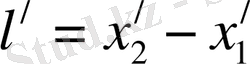 болады, мұндағы
болады, мұндағы
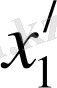 пен
пен
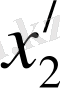 бұл шыбықтың екі ұшының уақытқа байланысты өзгермейтін
бұл шыбықтың екі ұшының уақытқа байланысты өзгермейтін
 координаталары. Уақыт өзгермеген жағдайда Лоренцше түрлендірудің (8) формулалары бойынша:
координаталары. Уақыт өзгермеген жағдайда Лоренцше түрлендірудің (8) формулалары бойынша:

сонда
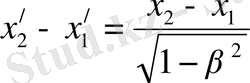 немесе
немесе
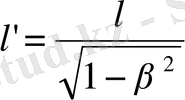 (9)
(9)
мұндағы
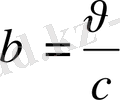 <1, сондықтан
<1, сондықтан
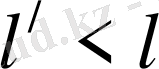 . Сөйтіп бір жүйеге қатысты қозғалып бара жатқан қатты шыбықтың сол жүйеде өлшенген ұзындығы
. Сөйтіп бір жүйеге қатысты қозғалып бара жатқан қатты шыбықтың сол жүйеде өлшенген ұзындығы
 оның өзімен салыстырғанда тыныш тұрған жүйеде өлшенген ұзындығынан
оның өзімен салыстырғанда тыныш тұрған жүйеде өлшенген ұзындығынан
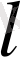 кем болады.
кем болады.
Түрліше жүйелердегі оқиғалар ұзақтылықтарын салыстыру
Жоғарыда айтылғандай екі санақ жүйесінен алайық. Мысалы
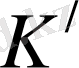 санақ жүйесіне қатысты бір тыныш тұрған нүктеде оқиға болған болсын. Сонда бұл оқиға осы
санақ жүйесіне қатысты бір тыныш тұрған нүктеде оқиға болған болсын. Сонда бұл оқиға осы
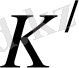 жүйесінде бір нүктеде
жүйесінде бір нүктеде
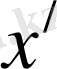 басталып, сол нүктеде бітетін болсын, сонда оның ұзақтығы
басталып, сол нүктеде бітетін болсын, сонда оның ұзақтығы
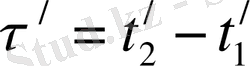 болады. Мұндағы
болады. Мұндағы
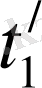
 мен
мен
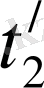 - оқиғаның
- оқиғаның
 - жүйе сағаты бойынша
- жүйе сағаты бойынша
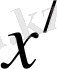 нүктеде басталып және сол нүктеде аяқталған мезеттері. Ал, оқиға болып жатқан нүкте
К
санақ жүйесіне қатысты
нүктеде басталып және сол нүктеде аяқталған мезеттері. Ал, оқиға болып жатқан нүкте
К
санақ жүйесіне қатысты
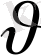 жылдамдықпен орын ауыстырсын. Сонда бұл
жылдамдықпен орын ауыстырсын. Сонда бұл
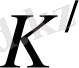 жүйесінде оқиғаның басына және аяғына сәйкес келетін уақыт мезеттері
жүйесінде оқиғаның басына және аяғына сәйкес келетін уақыт мезеттері
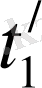 мен
мен
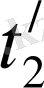 Лоренцше түрлендірудің (8) формуласы бойынша былай өрнектеледі:
Лоренцше түрлендірудің (8) формуласы бойынша былай өрнектеледі:
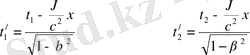
Сонда оқиғаның осы, К жүйесіндегі ұзақтылығы
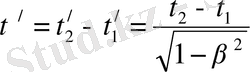 немесе
немесе
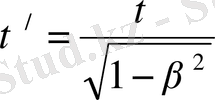 (10)
(10)
мұндағы
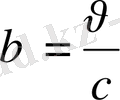 Equation. 3 <1, сондықтан
Equation. 3 <1, сондықтан
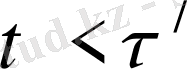 , яғни
, яғни
 уақыт аралығы К жүйесі сағаты (тыныш тұрған сағат), ал
уақыт аралығы К жүйесі сағаты (тыныш тұрған сағат), ал
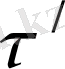 уақыт аралығы
уақыт аралығы
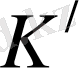 жүйе сағаты (қозғалыстағы сағат) бойынша өлшенген. Сөйтіп қозғалған сағат тыныш тұрған сағаттан гөрі баяу жүреді.
жүйе сағаты (қозғалыстағы сағат) бойынша өлшенген. Сөйтіп қозғалған сағат тыныш тұрған сағаттан гөрі баяу жүреді.
5. Жылдамдықтарды қосу теоремасы
Бұрын айтылғандай
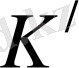 санақ жүйесі
К
санақ жүйесіне қатысты
х
осі бойымен
санақ жүйесі
К
санақ жүйесіне қатысты
х
осі бойымен
 жылдамдықпен қозғалып бара жатсын. Бір дене
жылдамдықпен қозғалып бара жатсын. Бір дене
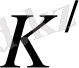 санақ жүйесінде сол
х
осінің бойымен
u
x
санақ жүйесінде сол
х
осінің бойымен
u
x
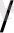 жылдамдықпен қозғалып бара жатқан болсын. Сонда бұл дененің
К
санақ жүйесіне қатысты жылдамдығы
u
x
қандай болады, соны есептелік.
жылдамдықпен қозғалып бара жатқан болсын. Сонда бұл дененің
К
санақ жүйесіне қатысты жылдамдығы
u
x
қандай болады, соны есептелік.
Бұл дененің
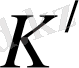 жүйесінде
жүйесінде
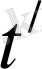 уақыт мезетіндегі координатасы
уақыт мезетіндегі координатасы
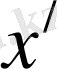
 болса, оның жылдамдығы
болса, оның жылдамдығы
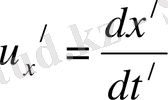 ,
К
жүйеге қатысты жылдамдығы
,
К
жүйеге қатысты жылдамдығы
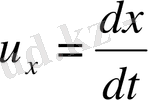
 , мұндағы
х
пен
t -К
жүйедегі координатасы мен мезет. Егер Лоренцше түрлендіру формулалары дұрыс келеді десек, онда (8) формулалар бойынша
, мұндағы
х
пен
t -К
жүйедегі координатасы мен мезет. Егер Лоренцше түрлендіру формулалары дұрыс келеді десек, онда (8) формулалар бойынша
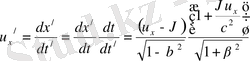 , бұдан
, бұдан
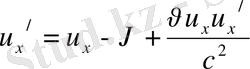
Яғни
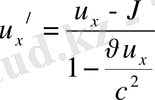 немесе
немесе
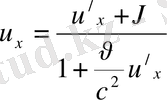 (11)
(11)
Осы (11) өрнек
жылдамдықты қосу теоремасы
деп аталады. Егер
 пен
пен
 әрқайсысы жарық жылдамдығынан әлде қайда аз болса, онда өрнек жылдамдықтары классикалық механикаша қосу, өрнегіне айналады:
әрқайсысы жарық жылдамдығынан әлде қайда аз болса, онда өрнек жылдамдықтары классикалық механикаша қосу, өрнегіне айналады:
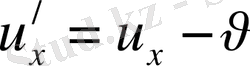 ,
,
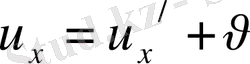
6. Материалдық нүктенің релятивистік динамикасының негізгі заңы
Қозғалыстағы релятивистік бөлшектердің массасы олардың жылдамдықтарына тәуелді:
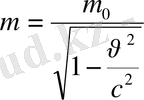 (12)
(12)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz