Фурье қатары мен арна сыйымдылығы: Найквист пен Шеннонның теоремалары және мәліметтерді жіберу тасымалдағыштары


Фурье қатары
ХІХ ғасыр басында француз математигі Жан Батист Фурье синус пен косинустардың қосындысынан құралатын Т периодты әрбір периодтық g(t) функциясы бір қатарда болуы мүмкін (мүмкін, шексіздік күйінде) екнін дәлелдеді:
Бұл жерде / = 1 / T - основная частота. (гармоника), а
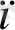 және b
және b
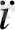 синус пен косинустың амплитудасы п гормоникасы, ал с константа функциясының осы жолмен қойылуы Фурье қатары деп аталады. Фурье қатарына қойылған функция осы қатардағы элементтермен қайта қалыптасып отырады, яғни бұл жердегі Т периодты гормоника амплитудасы белгілі, осыдан шыққан функцияның қорытындысы қатар сомасымен қайта қалыптасып отырады. (2. 1)
синус пен косинустың амплитудасы п гормоникасы, ал с константа функциясының осы жолмен қойылуы Фурье қатары деп аталады. Фурье қатарына қойылған функция осы қатардағы элементтермен қайта қалыптасып отырады, яғни бұл жердегі Т периодты гормоника амплитудасы белгілі, осыдан шыққан функцияның қорытындысы қатар сомасымен қайта қалыптасып отырады. (2. 1)
Соңы созылмалы ақпараттық сигналды (барлық ақпараттық сигналдардың соңы созылмалы болады) Фурье қатарына қоюға болады, егерде сигнал шексіздік күйінде қайталанып отыратын болса (яғни Т дан екі Т ға дейінгі интервал толығымен 0ден Г дейін қайталанып отыратын болса және т. б)
Әрбір g(t) фунциясының а
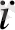 амплитудасы есептелінуі мүмкін. Бұл үшін қосындының оң жағы мен сол жағын (2. 1) sin (2nkft) көбейтіп 0 ден Т дейін интегралдау керек. Өйткені:
амплитудасы есептелінуі мүмкін. Бұл үшін қосындының оң жағы мен сол жағын (2. 1) sin (2nkft) көбейтіп 0 ден Т дейін интегралдау керек. Өйткені:
Бұдан бір қатар қалатын болғандықтан: а
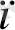 мен b
мен b
 қатары толығымен бірге жойылып кетеді. Сондай ақ, (2. 1) cos
қатары толығымен бірге жойылып кетеді. Сондай ақ, (2. 1) cos
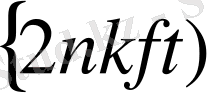 көбейтіп 0ден Т дейінгі уақытты интеграттап b
көбейтіп 0ден Т дейінгі уақытты интеграттап b
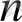 - ның тауып аламыз. Егер тендеудің екі жағын интеграттасақ оны өзгертпей ақ, онда с константаның мәнән табуға болады. Бұлардың қорытындысы төмендегідей болады.
- ның тауып аламыз. Егер тендеудің екі жағын интеграттасақ оны өзгертпей ақ, онда с константаның мәнән табуға болады. Бұлардың қорытындысы төмендегідей болады.
Шектелген спекторлы сигналдар
Жоғарыда айтылғандардың мәліметтерді жіберуге қандай қатысы бар екенін түсіну үшін “b” символды ASCII екнін кодты жіберу жөнінде нақты мысал арқылы қарастырамыз. Бұл үшін 8 бит қажет (яғни 1 байт) мақсатымыз 01100010 битті жіберу. Анализ нәтижесінде бұл сигналдын коэффицентінің мәнін табамыз:
Орта квадратты амплитуда
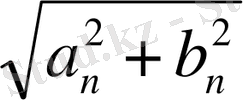 бірінші алдынғы гормоника сазанына арналады (2. 1) a. оң жақтағы. Бұл мән көрсетілген желіде жіберілетін пропорционалды энергияның квадраты болып табылады.
бірінші алдынғы гормоника сазанына арналады (2. 1) a. оң жақтағы. Бұл мән көрсетілген желіде жіберілетін пропорционалды энергияның квадраты болып табылады.
Ешбір канал сигналдарды қуаттылығын жоғалтпай жібер алмайды. Фурье қатарының барлық гармоникалары тең дәрежеде жібергенде азаймайды, онда сигнал амплитуда бойынша азаятын еді, бірақ таусылмайды ( яғни онда тікбұрышты форма болатын еді 2. 1, а) өкнішке орай Фурье қатарының гармоникасы барлық каналдың байланысын азайтады әртүрлі дәрежеде, сол себептен жіберілетін сигналды баяулатады. Ереже бойынша амплитудалар жиілік диапазоны 0 ден f
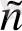 азаймай жіберілінеді ( секундтпен немесе герцпен (Гц) өлшенеді) сонымен жоғары желідегі сигналдың күші азаяды. Бұл диапазонның желісі жіберу жолы деп аталады. Тәжірибе жүзінде тоқтау (кесу) анағұрлым қатты болмайтындықтан жіберу жолынан 50% аспайтын желілер күштін жоғалуымен болады.
азаймай жіберілінеді ( секундтпен немесе герцпен (Гц) өлшенеді) сонымен жоғары желідегі сигналдың күші азаяды. Бұл диапазонның желісі жіберу жолы деп аталады. Тәжірибе жүзінде тоқтау (кесу) анағұрлым қатты болмайтындықтан жіберу жолынан 50% аспайтын желілер күштін жоғалуымен болады.
Жіберу жолының ортасы мәліметтерді жіберудің физикалық сипаты әдетте конструкцияның ұзындығы мен жалпақтығына байланысты болады. Кейде жіберу жолын әдейі азайту үшін абоненттерге мүмкін жеңіл қолда болатын арнайы құрылғы фильтр болады. Мысалы, кабильде телефон үшін қолданатын аз қашықтықтағы жіберу жолы 1 МГц бар, бірақта телефон компаниялары желісін фильтр арқылы оны кеседі тұтынушыларға тек 3100 Гц ті береді.
Мұндай жіберу жолы арқылы мәліметтерді анық жіберуге болады, өйткені әрбір абоненттің ресурстарының азаюы мен жалпы жүйенің тиімділігі артады.
Енді 2. 1 а) суретіндей сигналдың қандай екендігін қарастырайық егер тек ең төменгі желілер ғана өтетіндей болса жіберу жолы (яғни g(t) функциясы аппроксимировталған тек алдыңғы бірінші қатардағы теңдеудегі болса (2. 1) 2. 1, б суретінде каналдың шығатын жерінде сигналы көрсетілген, тек бірінші смигналдың гармоникасын өткізеді. Ұқсастығы бойынша 2. 1 в-g спектрды көрсетеді де сигналдарды қайта қалыптастырады кең жіберу жолы бар каналдар үшін.
Берілген жылдамдықтың жіберілуі битпен өлшенгенде bбит / с тең, уақыт, жіберуге тиісті 8бит, 8/b секундына тең болады. Бірінші гармониканың желісі
b/8 Гц тең қалыпты телефон линиясы сөздік канал деп аталатын 3000 Гц жасанды жасалған желісі бар. Бұл шектеулі түрде көрсететін ең жоғарғы гармониканың номері телефон каналымен өтетін, ол 3000(6/8) немесе 24000/6 тең болады.
2. 1 кестесінде көрсететіндей кейбір жылдамдықтағы мәліметтерді беруі көрсетілген. Айтылған мысалдан көріп тұрғанымыздай сөздік канал арқылы 9600 бит/с жылдамдығы мен жіберу 2. 1 а суретінде көрсетілген. Анығында 38400 с/бит жылдамдығымен жіберілген сигналдың ешбір амалы жоқ ол сөздік канал арқылы линияға ешбір кедергі болмаған жағдайда өте алмайды. Басқа сөзбен айтқанда шектеулі жолдағы желілер екінші мәліметтерді жібере алмайды, тіпті ешбір кедергі болмаған жағдайдың өзінде өтуі мүмкін емес.
Кесте 2. 1. Гармоник сандары мен жіберу жылдамдығының арақатынасы.
Ең жоғарғы жылдамдықта мәліметтерді канал арқылы жәберу(максималды)
1924 жылы АТ&T компаниясының ағылшын ғалымы Х. Найквист (H. Nyquist) қандай да бір күшті жылдамдық бар екені дәлелденді. Ол ең жоғарғы яғни максималды жылдамдықтағы мәліметтерді жіберудің теңдеуін ойлап тапты. Дыбыссыз каналдар мен шектеулі жіберу жолы бар желілер үшін. 1948 жылы Клод Шеннон (Claud Shannon) Найквисттің бастаған жұмысын жалғастырып және оның ауқымын кеңейтті. Ол кездейсоқ дыбыстарға да (яғни термодинамикалық) қатысы бар екенін көрсетті. Біз бүгінгі күнде классикалық түрге айналған Найквист пен Шеннонның жұмыстарын қысқаша қарастырайық.
Егерде өзіндік сигнал төмен жиілігі фильтрдан Я жіберу жолы арқылы өтетін болса, онда ондай фильтрленген сигнал түгелдей қалпына келе алады, 2# секундына желісімен өлшенетін сигналдың дискриттің мәнімен анықталатын Найквис дәлелдеген болатын. Сигналды 2 Я секундына артық өлшеу керек емес, өйткені сигналдың жоғарғы желімі компоненттері фильтрленген болатын. Егер Vсигнал дискреттік өлшенеді тұрса онда Найквистің теңдеуі былай болады.
Ең жоғарғы жылдамдықта мәліметтерді жіберу = 2H/log
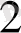 V, бит/с
V, бит/с
Мысалға дыбыссыз канал 3кГц желісімен жіберу жолы арқылы екінші сигналды 6000к бит/с жылдамдығымен жібере алмайды.
Сонымен біз дыбыссыз канал арқылы өту сигналын қарастырдық. Каналда қандайда бір дыбыстар пайда болатын болса жағдай күрт нашарлайды. Термодинамикңалық шудың көрсеткіш сигнал қуаты шу қуатының қатынасымен өлшенеді бұл өлшем сигнал/ шуылға қатынасы деп аталады. Егер сигналдың қуаты S, ал шуылдың қуаты N деп белгіленсе, онда сигналды/ шуға қатынасы S/N тең болады.
Әдетте бұндай жағдайда көлемнің қатынасы қолданбайды оның орнына ондық логарифм қолданады 10:10 lg S/N көбейтілген. Бұл сандық өлшем децибел ( decibel, dBgБ) деп аталынады. Сөйтіп 10 сигналдың/ шуылға қатынасы, бұл 10 gБ қатысты 100 дің қатынасы 20 gБ, ал 1000 қатынасы 30 gБ және т. с. с. стереусилительді шығаратындар көбінесе желімі жолындағы, аппаратурада сызықтық амплитуда желімін сипатты 3 gБ болады. 3gБ ауытқып кетсе сигнал кеі есеге нашарлап кетеді (өйткені log
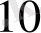 3 = 0. 5)
3 = 0. 5)
Шеннонның басты қорытындысы оң мәліметтерді максималды ең жоғарғы жіберу жылдамдығы Я Гц желісіндегі сигналдық/ шуылға қатынасы, S/N тең болса оны келесі формула арқылы есептей аламыз:
Мәліметтерді ең жоғарғы жылдамдықта жіберу= Hlog
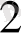 (1 + S/N)
(1 + S/N)
Мысалы, жіберу жолы арқылы 3000Гц сигналдың термальды 30 gБ/ шуылға қатынасы ешқашанда 3 бит/с аса алмайды сигнал модуляциясына қарамастан. Шеннонның қорытындысы ақпараттық теория постулаттары қайсыбір каналы Гаусовский (термалдық) шумен өте алады. Бұған қайшы теорияны дәлелдеу мүмкін емес. Бірақта айта кететін т бұл берілген жоғарғы теорема, ақпараттық каналдың теоретикалық жіберу жолы арқылы өткенде нақты жетуі кейбір жағдайда ғана болады.
Ақпаратты басқару құрылғылары.
Физикалық өлшемді көрсеткіші желідегі битті бір машинадан екінші машинаға жіберегенде пайда болады. Жіберу үшін әртүрлі ақпараттық басқару құрылғыларын қолдану үшін сигналды тарату аумағы деп аталатын. Бұлардың әрбіреуін жіберу жолы спатына ие болады оларды қолдану өте оңай болып табылады. Ақпаратты жіберу құрылғыларын екі топқа бөлуге болады: ақпаратты басқару құрылғылары, тез сым, кабель, радиоақпарат
және лазерлік жолмен кабель арқылы жіберу болып табылады.
Магниттік құрылғылары
Мәліметтерді бір компьютерден екінші компьтерге жіберудің ең қарапайым тәсілі ол мәліметтерді магнитті лентаға немесе басқада алынбалы құрылғыға жазып алу арқылы оларды осы лентаға жазып алып екінші компьтерден оқу болып табылады. Бұл тәсіл өте қарапайым болғандықтан геостационарлық спутниктің байланыста да экономикалық тұрғыдан тиімдірек болып табылады.
Лентаның жұмысын бақылауға келесі қиын емес теңдеулер көмектеседі. Ultrium деген жалпы касеталы лентаның сиымдылығы 200Г байт 60x60x60 размерлі қобдишаға 1000 кассета сияды, олардың жалпы сиымдылығы 1600 Т бит (1. 6 П бит) құрайды. Federal Express компаниясы арқылы АҚШ аумағына 24 сағат ішінде осындай қобдишалар жіберіліне алады. Тиімді жіберу жолы мұндай жіберуде 1600 Т бит/86400 с, немесе 19 Г бит/с болады. Егерде жіберілетін жер белгіленген жерден бір сағаттық жерде болса онда, жіберу жолының қуаттылығы 400 Г бит/с асады. Ешбір компьтерлік желі бұл көрсеткіштерге жетіп көрген емес.
Егерде біз ойлап елестетсек банктен көп гигабайтты мәліметтерді күнделікті архвировакттай отырсақ, магниттік лентаға жететін ешқандай технологияның жетпейтінін көрсетеді.
Егерде бұл жағдайды экономикалық тұрғыдан қарасақ онда магниттік кассетаның төмен бағамен есептегенде құны 40$ доллар. Ал магниттік лента салын кардиналар 4000$, бір лентаны оншақты рет қолдануға болатындығына қарамастан. $ 1000 доллар тасымалдау үшін. 200 Т бойынша жіберу үшін 5000$ доллар кетеді.
Елімізде ешқандайда желі бұл жүйенің бәсекелесе алмайды.
Бұдан ұғатын бір жайт ол: кассета толған автомавильдің дауысының шуына жоғарыдан қарамақ.
Витая пара
Магниттің лентамен мәліметтерді жіберу жылдамдығының өте жоғары болғанымен, жіберу жолында бөгделіктердің болуы мүмкіндігі де өте жоғары болатынын ұмытпау керек. Жіберу уақыты сағат пен минутпен өлшенеді, минисикундпен емес. Жіберуде көп қолданатын әдістердің бірі Битая пара болып табылады.
Бұл құрылғы екі диаметрі бір мм ді құрайтын изоляцияланған жез сымнан құралады. Сымдағы қозғалыстар спераль түрінде қозғалып отырады. ДНК малекуласына ұқсас. Витый пардағы элекромагниттік қатынасты азайтады.
Витый пардың көп тараған түрі ретінде телефон линиялары танылады. Барлық телефон компаниялары осы құрылғы арқылы қолданады. Витая пара бірнеше километрге дейінгі жерге сигналды қуатының азаймай жібере алады. Көп километрге алшақ жерлерге жіберуге Витая параға кабьел жалғанып сыртынан қорғаныс қабықшасымен қапталады.
3 категориялы Витая пара 2 түрлі сымнан құралады бір біріне изоляцияланған. Осындай 4 сым платикалық сырттың қорғаныстың ішінде болады. 1988ж. дейін кеңселерде 3 категориялы кабельдер қолданған болатын. 1988 жылдан бастап кеңселерде Б категориялы Витая параға ұқсас бірақ оған қарағанда көбірек виталары бар және ұзындығы ұзынырақ болады. Бұл оның ұзақ қашықтыққа мәліметтерді жібергенде сапасы жоғары. 5 категориялы витые пара жоғары жылдамдықты компьютерлік ақпаратты жіберуге қолайлырақ болып келеді. 250, 600 МГц ті жіберу жолы бар 6, 7
Категориялы витая паралардың ойлап табылынуы мүмкін.
Осы типтер көп жағдайда UTP ( unshielded twisted pair экрандалынбаған витая пара) қосылуы деп аталады. IBM корпарациясының витые парасына қарама-қарсы, 1980 жылы қолданысқа енген. IBM нің шеңберінен шыға алмай қалған. UTP әртүрлі схеманық түрде 2. 2. ceретінде көрсетілген.
Басқада көп қолданысқа ие мәліметтерді жіберудің түрі ноаксимальды кабель болып табылады. Ол витая параға қарағанда экрандалған сол себептенде ол алшақ қашықтыққа жоғары жылдамдықпен жіберілінеді. 2 типті кабель кең ауқымда қоланылады. Солардың ішіндегісі 50 омдық цифрлық мәліметтерді жіберу үшін қолданылады. Екіншіс 75 омдық ол ақпатаратты жіберуге және де кабельдің телевидианада мәләметтерді жіберуге қолданылады.
Коасикольды кабель изоляциямен қапталған қатты жез сымнан, кабельдің ортасында орналасқап тұрады. Ұсақ жез сетка сияқты безендірілген целиндірлік изоляциямен қапталған. Ол сыртқы изоляциялық қапташаман қапталған кабельдің суреті.
Коаксикальды кабельдің арнайы экрандалған типі кабельге жоғарғы жіберу жолын қамтамасыз етеді. Қазіргі кездегі кабельді 1ГГц жіберу жолы бар. Коаксикальды кабель телефон жүйесінде қолданған, бірақ қазіргі күнде осы оптоволоконды кабельдермен алмастырылған. Бірақта коаксикальды кабельді телевидения жү. йесінде және кейбір аумақтық жүйелерде кең ауқымда қолданылады.
Волокомдық оптика
Кампьютерлік технологияның ауқымды дамуы осы индустрия саласының қызметкерлерін қуантады. 1981жылы IBM фирмасының алғашқы компьютері 4, 77 МГц желісімен құрылған. 20жыл өткеннен кейін ол көрсеткіш 2 ГГц дейін өскен. Оптоволоконды мәліметтерді жіберу жуйесі үш манызды компоненттерден тұрады. Сәулелі импульсті бір десек, ал импульстін жоқтыгын нольмен белгілейміз. Сәуле өте жұқа шыны волокон арқылы тарайды. Детекторға сәуленін түсуі электорлық импольсті генеруривать етеді. Оптикалық волокнаны сәуленін шығу тетігіне, ал екінші жағын детекторға жалғасақ бір жүйелі мәләметтерді жіберуге болады. Бұл жүйе электрондық сигналдарды сәулелік имплюске жіберіп оны волоконға қосады. Бүгінгі күндегі бірлік волокондар 50 Гбит / жылдамдықпен бір секунтта 100 км қашықтыққа дейін жіберіледі. Лабороторияда бұдан да жоғары аз қашықтыққа көп жылдамдыққа ие болған.
Сәуленің волокон арқылы өтуі.
Оптикалық волокон шыныдан жасалынады, ол өз кезегінде қымбат емес материал мен құмнан жасалынған. Шыны жасау ежелгі Египетте пайда болған, бірақта сәуле шыныдан өту үшін оның қалындығы 1мм болу керек болды, ол кезде бұны істеу мүмкін емес болатын. Шынының мөлдір болуы, қайта өрлеу дәуірінде пайда болды. Қазіргі кездегі оптикалық кабельдегі шынылар мөп мөлдір.
Сәуленің өтуінің азаюы шыны арқылы толқынның ұзындығына байланысты 2, 5 суретінде көрсетілгендей толқынның ұзындығы дицибельмен километр ұзандық ауытқуы оптикалық волокондағы шыныда қолдануға болады. Децибеид ауытқушылық болудың формуласы:
Ақпарат жүйесінде үш диопозонды толқын ұзындығы болады олар: 0, 85, 1, 30, және 1, 55 мкм соңғы екеуі жақсы ауытқушылықтарға ие болып келеді.
0, 85 мкм диапазоны жоғарғы ауытқушылыққа ие болып келеді, осы ұзындық үшін лазерлік электроникалық толқындар бір материалдан жасалынуы мүмкін. Барлық үш диапазонда 25000, 3 Гц дейінгі жіберу жолына ие болып келеді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz