Желідегі қателерді табу және дұрыстау алгоритмі

КІРІСПЕ

1 АҚПАРАТТЫҚ ЖҮЙЕ МЕН АҚПАРАТ ҚАУІПСІЗДІГІН САҚТАУДЫҢ ҚАЖЕТТІЛІГІ 1.1 Желіде кездесетін қатерлердің түрлері
1.2 Түзету кодтарының импульсивті кедергілер кезінде тиімділігі

2 ЖЕЛІДЕГІ ҚАТЕЛЕРДІ ТАБУ ЖӘНЕ ДҰРЫСТАУ АЛГОРИТМІ
2.1 Рид . Соломон кодтарымен қателерді түзеу жолдары
2.2 Деректерді тасымалдау кезінде пайда болатын қателер

ҚОРЫТЫНДЫ

ҚОЛДАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ

Қазіргі ақпараттық ғасырда деректерді жіберу, сақтау және іздеу үшін тек қана оның жылдамдығы маңызды емес, сонымен қатар оның қатесіздігі маңызды. Бұл мәселені шешудің бір жолы кедергіге тұрақты кодтауды пайдаланылады. Бұл кодтар блоктық екілік емес, қателерді түзеуші кодтарға жатады, олар тәуелсіз және түзетілген (дестелерді) қателерді тауып және түзетуді қамтамасыз етеді. Қазіргі таңда Рид-Соломон коды пакеттерде көп қолданылатын қателерді түзету мақсатында кең ауқымда қолданылуда. Сонымен бірге тез әрекеттілігі (кодтау және декодтау жылдамдығы), жүзеге асырылу қиындығы (бағдарламаның көлемі немесе құрылғылардың шағыны), әмбебаптылығы сияқты көрсеткіштер де ескеріледі. Барлық параметрлерді ең жақсы жағдайда қамтамасыз ету мүмкін еместігі анық, және әрбір нақты жағдайда шешімді жеке-жеке жағдайларда қабылдау керек.
Осы жұмыстың мақсаты: Желідегі қателерді тауып, оларды түзету жолдарын көрсету.
Курстық жұмыстың мақсатына жету барысында келесі мәліметтер орындалады:
• ақпараттық жүйе мен ақпарат қауіпсіздігін сақтаудың қажеттілігі мен бірге желіде кездесетін қатерлердің түрлері, түзету кодтарының импульсивті кедергілер кезінде тиімділігін қарастыру;
• желідегі қателерді дұрыстау алгоритмі: Рид – Соломон алгоритмде қателерді түзеу жолдары, деректерді тасымалдау кезінде пайда болатын қателерді табу.

1. Алдажаров Қ.С. Компьютерлік желілер: Оқу құралы. – Алматы: Экономика, 2010ж. – 144 бет.
2. Компьютерные сети. Принципы, технологии, протоклы: Учебник для вузов. 2-е изд. /В.Г.Олифер, Н.А.Олифер.-СПб: Иэдательство «Питер», 2010г.-864с.:ил.
3. Компьютерные сети: учеб. пособие по администрированию локальных и объединенных сетей / А. В. Велихов, К. С. Строчников, Б. К. Леонтьев ; . - 3-е изд., испр. и доп. - М. : Новый издат. дом, 2010г. - 304 с.
4. Таненбаум, Э. Компьютерные сети : научное издание / Э. Таненбаум. - 4-е изд. - СПб. : Питер, 2011г. - 992 с.
5. Форни Д. Каскадные коды. – М.: “Мир”, 2012г. – 207 c.
6. Вернер М. Основы кодирования. – М.: “Техносфера”, 2011г. – 288 с.
7. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 2012г. — С. 596.
8. Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 2012. — 576 с.
9. Берлекэмп Э. Алгебраическая теория кодирования = Algebraic Coding Theory. — М.: Мир, 2010г. — С. 478.
10. Егоров С.И. Коррекция ошибок в информационных каналах периферийных устройств ЭВМ. — Курск: КурскГТУ, 2011г — С. 252.
11. Сагалович Ю. Л. Введение в алгебраические коды: Учебное пособие. — М.: МФТИ, 2010г. — 262 с. — ISBN 5-7417-0191-4
12. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева. — М.: Техносфера, 2011г. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0
13. М. Вернер Основы кодирования. — Техносфера, 2011г. — 288 с. — ISBN 5-94836-019-9
14. В.М. Охорзин, Д.С. Кукунин, М.С. Новодворский - Построение каскадных кодов на основе кодов Боуза – Чоудхури – Хоквингема
и Рида – Соломона. Методические указания по курсовому проектированию. 2011г.- 547 с.
15. Блох Э.Л., Зябло С# в В.В. Обобщенные каскадные коды. –М.: Связь,2010г.
16. Коржик В.И., Финк Л.М. Помехоустойчивое кодирование дискретных сообщений в каналах со случайной структурой. – М.: Связь, 2011г.
17. Кларк Дж. мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. – М.: Радио и связь, 2011г.
18. Сидельников В.М. О спектре весов двоичных кодов Боуза-Чоудхури-Хоквингема.Проблемы передачи информации N1 2012г.
19. Сидоренко В.М. Верхняя граница мощности q-ичных кодов. Проблемы передачи информаци N3 2010г.

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 27 бет
Таңдаулыға:

КІРІСПЕ

Курстық жұмыстың тақырыбы: Желідегі қателерді табу және дұрыстау
алгоритмі.
Курстық жұмыстың өзектілігі: Қазіргі ақпараттық ғасырда деректерді
жіберу, сақтау және іздеу үшін тек қана оның жылдамдығы маңызды емес,
сонымен қатар оның қатесіздігі маңызды. Бұл мәселені шешудің бір жолы
кедергіге тұрақты кодтауды пайдаланылады. Бұл кодтар блоктық екілік емес,
қателерді түзеуші кодтарға жатады, олар тәуелсіз және түзетілген
(дестелерді) қателерді тауып және түзетуді қамтамасыз етеді. Қазіргі таңда
Рид-Соломон коды пакеттерде көп қолданылатын қателерді түзету мақсатында
кең ауқымда қолданылуда. Сонымен бірге тез әрекеттілігі (кодтау және
декодтау жылдамдығы), жүзеге асырылу қиындығы (бағдарламаның көлемі немесе
құрылғылардың шағыны), әмбебаптылығы сияқты көрсеткіштер де ескеріледі.
Барлық параметрлерді ең жақсы жағдайда қамтамасыз ету мүмкін еместігі анық,
және әрбір нақты жағдайда шешімді жеке-жеке жағдайларда қабылдау керек.
Курстық жұмыстың мақсаты: Желідегі қателерді тауып, оларды түзету
жолдарын көрсету.
Курстық жұмыстың мақсатына жету барысында келесі мәліметтер
орындалады:
• ақпараттық жүйе мен ақпарат қауіпсіздігін сақтаудың қажеттілігі мен
бірге желіде кездесетін қатерлердің түрлері, түзету кодтарының
импульсивті кедергілер кезінде тиімділігін қарастыру;
• желідегі қателерді дұрыстау алгоритмі: Рид – Соломон алгоритмде
қателерді түзеу жолдары, деректерді тасымалдау кезінде пайда болатын
қателерді табу.
Бірінші бөлімде

1 АҚПАРАТТЫҚ ЖҮЙЕ МЕН АҚПАРАТ ҚАУІПСІЗДІГІН САҚТАУДЫҢ ҚАЖЕТТІЛІГІ
1.1 Желіде кездесетін қатерлердің түрлері

Жаңа ақпараттық технологияның және жаппай компьютерлендірудің дамуы
ақпараттық қауіпсіздіктің тек міндетті ғана емес, сонымен бірге желілердің
сипаттарының бірі болуына алып келді. Оның үстіне, қауіпсіздік факторын
әзірлеуде ақпаратты өңдеу жүйесінің кең жіктері бірінші дәрежелі рөлге ие
болады (мысалы, банктің ақпараттық жүйелері).
Желілердің қауіпсіздігі деп жүйенің ақпараттардың қалыпты жұмысына
оқыстан немесе қасақана араласушылықтан, жымқыруға тырысудан
(санкцияланбаған алудан), оның компоненттерін түрлендіруден немесе нақтылы
бұзуға әрекет жасаудан қорғауы түсініледі. Басқаша айтқанда, бұл –
желілердің жасалатын түрлі әрекеттерге қарсы тұру әрекеті.
Ақпараттың қауіпсіздік қатесі дегенде оны бұрмалауға, санкцияланбаған
пайдалануға немесе тіпті басқарылатын жүйенің ақпараттық ресурстарының,
сондай-ақ программалық және аппараттық құралдардың бұзылуына алып келуі
мүмкін әрекеттер немесе оқиғалар түсініледі.
Егер кез келген басқарылатын жүйенің кибернетикалық үлгілерінің
дәстүрлі қарастыруларынан шығаратын болсақ, оған қарсы әрекеттер кездейсоқ
сипатта болуы да мүмкін. Сондықтан, ақпараттардың қауіпсіздігіне қатерлер
кездейсоқ немесе ниеттенбеген деп бөлінуі тиіс. Олардың көздері желілердің
қызметкерлерінің теріс әрекеттері, аппараттық құралдардың істен шығуы
немесе оны пайдаланушылардың программалық қамтудағы ниеттенбеген
қателіктері және т.б. болуы мүмкін. Мұндай қатерлерден келетін залалдар
мәнді болуы мүмкін, сондықтан олар назардан тыс қалдырылмауы тиіс. Алайда,
осы тарауда қасақана жасалған қауіптерге көбірек назар аударылады,
кездейсоқ жасалғандарға қарағанда басқарылатын жүйеге немесе
пайдаланушыларға әдейілеп жасалған қауіптердің көздеген мақсаттары болады.
Бұл, көбінесе, жеке басының пайдасын көздеуден жасалады.
Желілердің жұмысын бұзуға әрекет жасаған адам немесе ақпараттарға
санкцияланбаған қолжетімділікті иеленгісі келген жан, әдетте, қарақшы,
кейде компьютерлік пират (хакер) деп аталынады. Қарақшылар өздерінің
бөгденің құпияларын меңгеруге бағытталған заңға қарсы әрекеттерінде, оларға
аз шығын жұмсай отырып, көп көлемде анық ақпарат алуға көмектесетін жасырын
ақпараттардың көздерін табуға ұмтылады. Көптеген әдістер мен тәсілдерді
пайлана отырып, әр түрлі амал-айлаларды ізедстіріп, осындай негіздерге қол
жеткізетін жолдарды пайдаланады. Бұл жағдайда ақпарат негіздеріне ниеті
бұзықтар мен бәсекелестер үшін нақтылы мүдде ұсынатын анықталған
мәліметтері бар материалдық обьект жатады.
Қасақана қателерден қорғану – бұл қорғаныс пен шабуыл жарысы сияқты:
кім көп білсе және әрекеттерін алдын ала болжай алса, сол жеңіп шығады.
Соңғы жылдардың көптеген басылымдары желілердің ақпараттың теріс
пайдаланылуы, айналымда таралуы немесе байланыс арналары бойынша берілуі
олардан қорғаныс шараларынан көбірек жетілдірілгенін көрсетеді. Қазіргі
уақытта ақпаратты қорғауды қамтамасыз ету үшін тек қорғаудың жеке
тетіктерін жай ғана әзірлеп қана қоймай, сонымен бірге өзара байланысты
шаралардың кешенін ендіретін (арнайы техникалық және программалық құралдар,
ұйымдастырушылық шаралар, нормативті-заңдық актілер, моралды-этикалық қарсы
әрекет ету шаралары және т.б.) жүйелі тәсілді жүзеге асыруда талап етеді.
Қорғаныстың кешенді сипаты өздері үшін кез келген құралдармен маңызды
ақпарат алуға ұмтылған теріс ниеттілердің кешенді әрекетіне бағытталады.
Сондықтан ақпаратты қорғау технологиясы желілердің мен АТ қатерлерін жүзеге
асыруда туындауы мүмкін аса көп шығындар мен жоғалтулардың алдын алуға
мүмкіндік беретін осы мәселеге тұрақты назар аудару мен шығындарды талап
етеді.

Желідегі кептелістерді болдырмау бұл проблеманы шешу үшін келесі
жағдайды қарастырамыз: коммутация түрі келесідей 1- суретте
көрсетілген.[1]

1-сурет. Түйіндердің өзара қатынасы

Бірінші компьютер жіберген мәлімет алтыншы компьютерге қандай
жылдамдықпен тасымалданатынын қарастырайық.
1-түйіндегі мен 2-түйіндегі пакеттер параллельді түрде тасымалданса, 3-
түйінде олардың жылдамдығы 3 Мбитс болады. Ал 3-түйінде оны жіберуге
мүмкіндігі жоқ болса, онда кептелістер пайда болады. Осындай кептелістерді
болдырмау үшін желідегі программалық жабдықтауда арнайы программалар болуы
және хаттамалрда осы жағдайды бақылауға, оны табуға мүмкіндіктер болуы
қЖелілердіңет.
Кептелістерді болдырмау үшін 2 тәсіл қолданылады:
1. Кептелістер болған жағдай туралы берушіге ескертуді жіберу;
2. Пакеттердің жоғалғаны туралы ақпаратқа сүйене отырып кептелістер
қауіпсіздігін бағалау.
Іске асыру үшін коммутаторда кептелістер туралы арнайы хабар
пайдаланылады немесе әр пакеттің тақырыбында арнайы битті көрсету
пайдаланылады. Егер осы бит қойылған болса, онда пакетті қабылданғанын
растауға компьютер сигналына осы ақпаратты қосады.

1.2 Түзету кодтарының импульсивті кедергілер кезінде тиімділігі

Әрбір символы т = 8 биттен тұратын ( мұндай символдарды байт деп
аталуға қабылданған ) (n, k) = (255, 247) кодты қарастырайық. п-k=8
болғандықтан, (1.1.4) теңдігінен көруге болады: бұл код 255 ұзындықтағы
блоктағы кез – келген 4-символдық қателерді түзей алады. 25 бит ұзындықтағы
блок жіберілу жүрісі кезінде кедергілерге тап болсын делік.
25 тізбектелген битке түсетін шу дестелері тура 4 символды бұрмалайды
ол төмендегі 3-суретте көретілген. (255, 247) коды үшін декодер кез –
келген 4-символдық қателерді символдың бұзылу сипаттарына қарамай түзей
алады. Басқаша айтсақ, егер декодер байтты түзейтін (бұрысын дұрысымен
алмастырады) болса, онда қате бір биттің немесе барлық сегіз биттердің
бұрмаланғанымен шақырылған болады. Сол себепті егер символ дұрыс емес
болса, ол барлық екілік позицияда бұрмалануы мүмкін.
Рид-Соломон кодтары (Reed-Solomon code, R-S code) - бұл екілік емес
циклдық кодтар, оның символдары т – биттік тізбекті құрайды, мұндағы т – 2
санынан үлкен оң бүтін сан. Бұл екілік кодтармен салыстырғанда импульстік
кедергілер кезінде Рид-Соломон кодына үлкен артықшылық береді (тіпті екілік
кодта алмасуларды қолданғанның өзінде). Бұл мысалда егер 25 биттік
кездейсоқ кедергі қаралатын болса, 4 символдан да артық бұрмалануы
мүмкіндігі анық көрінеді, ол төменде 2-суретте көрсетілген.[6]

2-сурет. 25 бит ұзындықтағы блок

Рид-Соломон кодының функция өлшемі, артықшылығы мен кодтаудың
дәрежелері сияқты негізгі сипаттамалары.
Код шу эффекттерiне ойдағыдай қарсы тұру үшін кедергілердің ұзындығы
кодтық сөздердің санының санына қатысты үлкен емес пайыздық мөлшерін құрауы
тиіс. Осылайша ұзақ мерзімде болатынына сенімді болу үшін, қабылданған шуды
ұзақ мерзім аралығында ортақ шамаға келтіру керек, осылайша нашар
қабылданудағы кенеттен немесе ерекше жолақтардың эффектілерін азайтады.
Сондықтан қателерді түзейтін код жіберілуші блоктың өлшемін арттыру кезінде
(берілудегі сенімділік көтеріледі) әлдеқайда тиімді болады, бұл Рид-Соломон
кодын тиімдірек көрсетеді, егер блоктың ұзындығы үлкенірек болса. Мұны
көрсетілген қисықтар жиыны бойынша бағалауға болады және ол 4-суретте
көрсетілген, ол жерде кодтау дәрежесі 78 тең деп алынған, блок ұзындығы n
= 32 символдан ( символға w = 5 биттен келеді ) n=256 символға дейін
өседі.
Осылайша, блок мөлшері 160 биттен 2048 битке дейін өседі.
Кодтың артықшылығының үлкею шарасы бойынша ( және оның кодтау
дәрежесінің төмендетулері) бұл кодтың жүзеге асырылу қиындығы жоғарылайды
(әсіресе жоғарғы жылдамдықты құрылғылар үшін). Сонымен бірге нақты
уақыттағы байланыстағы жүйелер үшін өткiзу жолағының енi үлкеюi керек.
Артықшылықтың үлкеюi, мысалға символ өлшемінің үлкеюі, биттік қателердің
пайда болу ықтималдығының азаюына әкеледі, сонымен бірге п кодтық ұзындық
мәлiметтердiң символдарының санының төмендетуiнде k = 60 мәнінен k = 4 ке
дейін (артықшылық 4 тен 60 символға дейін өседі) тұрақты 64 мәніне тең.
Гипотеза декодерлерiнің беріліс функциясы (кіріс символдық қателердің
пайда болу ықтималдығынан тәуелді шығыс биттік қателердің пайда болу
ықтималдығы. Себебі бұл жерде анықталған жүйе немесе канал ескерілмейді
(тек декодердің кірісі мен шығысы), берiлудi сенiмдiлiк артықшылықтың бiр
қалыпты функциясы болып табылатынын және кодтау дәрежесінiң нөлге
жуықтауымен өсетiнi жөнінде қорытынды жасауға болады. Символ өлшемінің
функциясы ретінде (кодтау дәрежесі= 78 ) Рид-Соломон декодерінің
сипаттамалары 3-cурет көрсетілген. Ал Рид-Соломон декодерінің артықшылық
функциясы ретінде сипаттамалары 4-cуретте көрсетілген [2] .

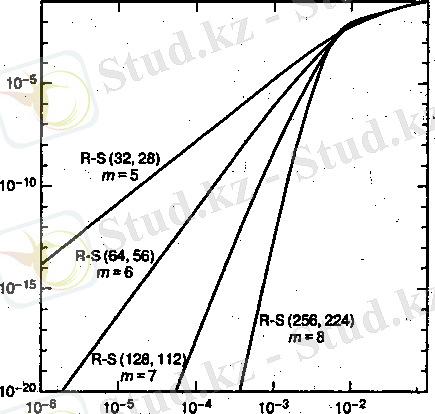
3-cурет. Символ өлшемінің функциясы ретінде (кодтау дәрежесі= 78 )
Рид-Соломон декодерінің сипаттамалары.

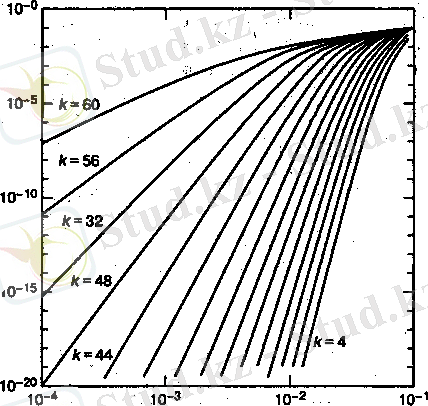
4-cурет. Рид-Соломон декодерінің артықшылық функциясы ретінде
сипаттамалары.
Бірақ бұл нақты уақыттың байланыс жүйесінде қолданылатын код үшін
емес. Кодтың максимальді мәнінен минимальді мәніне дейін (0 ден 1 ге дейін)
кодтау дәрежесінің өзгеру шарасы бойынша көрсетілген эффектілерді көруге
болады (сурет 6). Мұнда жұмыстың қисықтық мiнездемелері екiлiк фазалық
манипуляциясы (BPSK) кезінде және әр түрлі типтегі каналдардың (31, к)
кодтарында көрсетілген.
Нақты уақыттағы байланыс жүйелері, бұл жүйеде қателерді түзетудегі
кодтауына кодтаудың кері дәрежесіне тең көлеміне пропорционал келетін
өткiзу жолағының кеңейтуiмен төлеуге тура келеді. Келтірілген қисықтар
тиiстi мәнді 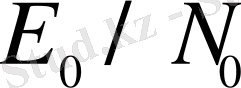минималдайтын кодтау дәрежесінің айқын ұтымдылығын
көрсетеді.
Гаусстық канал үшін кодтау дәрежесінің ұтымды мәні 0,6 және 0,7
мәндері аралығында жатады, райсовкілік қатуымен каналы үшін 0,5 шамасында
(түзу сигнал қуаттылығының шағылған К = 7 дБ қуаттылығына қатынасы) және
0,3 -релеевті қатуы бар канал үшін. Неге мұнда кодтаудың өте жоғарғы
дәрежесінде де (аз артықшылықта) және өте төменгі (артықшылықтың көп
болуында) дәрежесінде де 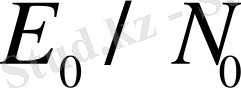нашарлауы байқалады. Кодтаудың жоғарғы
дәрежесі үшін кодтаудың жоғарғы дәрежесін кодтаудың ұтымды дәрежесімен
салыстыра отырып мұны түсіндіру оңай.
Қателердің пайда болу ықтималдылығының кодтау дәрежесінен тәуелділігін
2-суретте көрсетілгендей қисықтардың көмегімен растап көрейік. Суреттерді
тікелей салыстыру сәтті болмайды, себебі 6-суретте BPSK (екiлiк фазалық
манипуляциясы) модуляциясы қолданылады, ал 2-суретте 32-лік MFSK
(манипуляцияның бiрнеше жиiлiктерi) модуляциясы. Кодтау дәрежесінің (BPSK
модуляциясы) функциясы ретінде (31, k) Рид-Соломон декодерінің
сипаттамалары төменде 5-суретте көрсетілген [2].

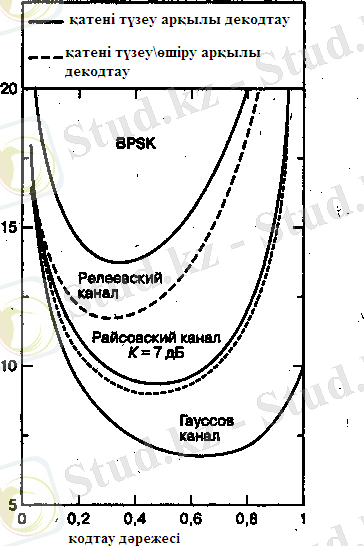
5-сурет. Кодтау дәрежесінің (BPSK модуляциясы) функциясы ретінде (31,
k) Рид-Соломон декодерінің сипаттамалары.

2 ЖЕЛІДЕГІ ҚАТЕЛЕРДІ ТАБУ ЖӘНЕ ДҰРЫСТАУ АЛГОРИТМІ
2.1 Рид - Соломон кодтарымен қателерді түзеу жолдары

Желідегі қателерді табу және дұрыстау алгоритміне екі алгоритм түрі
қарастырылады, олар: кері таратылу алгоритмі және тектік алгоритмдер.
Нейронды желілерде (НЖ) кері таратылу алгоритмі көп қолданылады, ол
қысқа уақыт аралығында (қор нарықтарындағы алаяқтық операциялар,
бағамдардың қысқа мерзімді болжамданулары, техникалық талдау және т.б.)
шешімдерді қабылдау мен ақпараттардың үлкен көлемдерін өңдеумен байланысты
болжамдар мен бағалау алуды талап ететін қаржылық және инвестициялық
менеджменттің аумақтарында кең қолдау тапқан. НЖ мынадай жетістіктерін
бөліп көрсетеді: желісіз үдерістерді болжамдау және үлгілендіру мүмкіндігі;
шулы мәліметтермен жұмыс істеуге қабілеттілік; сыртқа ортаның өзгерістеріне
икемді бейімділік.
НЖ шығулар мен енулердің қара жәшігі ретінде қарастырған қолайлы
болады. Ену мәндері ауыспалы желі ішінде өңделеді және нәтижелері шығуларда
бейнеленеді. Мұндай жүйенің шешуші айырмашылығы, енетін ақпараттарды өңдеу
үдерісінде ішкі құрылым желісінде, яғни қайта өзгеру алгоритмінде өзгеріс
өтетіндігінде. Бұл үдеріс оқыту деп аталады және НЖ қатаң программалық
жүйелерден түбірімен ерекшелендіреді. Оқыту үдерісінде желілерде
мәліметтердің енетін мысалдары көрсетіледі, ал алынған мәліметтердің
шығуында эталондармен салыстырылады. Оқыту үдерісі кейбір қолданбалы
нәтижеге қол жеткізуде (қате деңгейінде) аяқталады. Егер жауаптар сәйкес
келмесе, желі құрылымы қатені азайтуға ауыстырылады. Оқыту үдерісі кейбір
қолайлы нәтижеге (қате деңгейіне) қол жеткізуде аяқталады. Мұндай тетік
кері таратылу алгоритмі (back-propagation algorethm) деген атау алған.
Тектік алгоритмдер НЖ оңтайлы шешімдерді іздеуге арналған биологиялық
эволюцияның тетігін пайдаланатын, салыстырмалы жаңа бағытын көрсетеді.
Оңтайландырудың дәстүрлі әдістеріне қарағанда тектік алгоритмдер нақты
емес, ал күрделі, оның ішінде желісіз, қомақты мөлшерлі міндеттерді шешуге
қолайлы шешімдер табуға мүмкіндік береді.
Тектік алгоритмдер жалпы жағдайда көптеген шығатын нүктелерден бір
уақытта тегістікті абстрактылы зерттегенде, ауқымды түсетін алуан түрлі
әдістерді көрсетеді. Оңтайландырудың әрбір қадамында өзгермелі түрлі
мәндердің қындастырылуына сәйкес жаңа көптеген шығатын нүктелердің тууы
(жаңа таратылу) өтеді. Бұл жерде тоғысудыңмұра етудің (crossover
параметрі) талап етілген деңгейі міндеттеледі, мысалы –0,8, яғни әрбір
нүкте үшін берілгеннен қатенің ағымдағы мәнінің ауытқуы (сәйкестік
функциясы деп аталатын) есептеледі және оңтайландырудың келесі қадамы
қателерді азайту мағынасында ең үздік көрсеткіштер көрсеткен алдыңғы
нүктелердің 80%-ы жүргізілетін болады.
Міне, осы жағдайда мутация факторы (mutation параметрі), мысалы 0,20
міндеттелінеді. Яғни, оңтайландырудың әрбір қадамында (жаңа таралымда) 20%-
да ауыспалы сәйкесті мәндердің өзгеру қаыстық заңы бойынша жүргізілетін
болады. Қаншалықты әрбір келесі ұрпақ алдыңғылардың ең жақсы белгілерін
мұра ететіндіктен, бұл жағдайда – (кезеңдік мутация есебімен аз ғана қате
жағынан қоғалыс бағытымен), ең соңында қорытындысында мақсатты қызметтен
ауытқу үшін кейбір көптеген нүктелер алады.
Бұл жерде, тектік алгоритмді оңтайландыру көптеген-ықтималдықтар болып
табылады, яғни шығатын шарттарға жуық сәйкесетін көптеген мәндер табуға
мүмкіндік береді. Бұл жағдай максимум немесе минимум айқын емес бейнеленген
маңызды есептерді шешуге арналған.
Қазіргі уақытта тектік алгоритмдерді жеткілікті тиімді жүзеге асыратын
бірнеше программалық өнімдер бар. Олардың ішіндегі қаржылық-кредиттік
саладағы ең кеңінен танымалы – Evoler (Palisade Corp.,США ) GeneHunter
(Ward Systems, США), Omega (KiQ and CAP, США) өнімдері болып табылады. Ең
қызығы, алғашқы екеуі MS Excel қондырмасы түрінде жүзеге асырылған және
Visual for applications (VBA) тілінде жазылған. Өнімдердің екеуі де
тұтастай алғанда өзінің қызметтік мүмкіндіктері бойынша ұқсас.
Рид-Соломон кодтарының (2.1) теңдігінде ішінде ең көп таралған формасы
n, k, t параметрлері арқылы және кейбір m 2 оң саны арқылы көрсетілген.
Осы теңдікті қайта келтірейік.

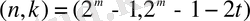(2.1)

мұндағы 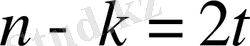- бақылау символдарының саны, ал t – символдағы қатілік
битінің саны, оны код түзете алады. Рид-Соломон коды үшін арналған
генерациялайтын полином келесідей түрге ие.

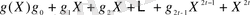( 2.2)
Полиномды генератор дәрежесі бақылау симводарының санына тең. Рид-
Соломон кодтары БЧХ (Боуза - Чоудхури - Хоквингхема) кодының ішкі жиыны
болып табылады. Сол себепті БЧХ кодтарындағыдай полиномды генератор
дәрежесі мен бақылау символдары арасындағы байланыстың болғаны күтпеген
жағдай емес. Сондықтан полиномды генератор 2t қатарына ие, біз нақты
полином түбірі болып келетін дәрежесінің нақты тізбектілігін алуымыз
керек. 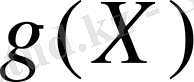түбірлерін 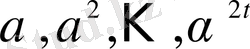деп белгілейміз.
Тек қана түбірінен бастаудың қажеттілігі жоқ, мұны – ның
кез келген дәрежесінің көмегімен жасауға болады. Екі символдық қателерді
түзету мүмкіндігі бар (7,3) кодты мысалға алайық. Біз түбірі арқылы
полиномды генераторды келесідей өрнектейміз.

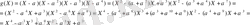( 2.3)

Рид-Соломон коды циклдық болғандықтан систематикалық формада кодтау
екілік кодтауға ұқсас. m(X) хабарламасы полиномын кодтық сөздің регстрінің
оң жақ шеттегі k разрадтарына жылжыта аламыз және келесі p(X) ақиқаттық
полиномын сол жақ шеттегі n – k разрядтарына қоса аламыз. Сол себепті m(X)
– ті 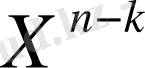– ке көбейтеміз, осылайша алгебралық операцияны орындай отырып,
m(X) оңға қарай n – k позицияға жылжыған болады. Одан кейін 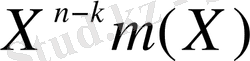– ті g(X)
полиномды генераторына бөлеміз, оны келесідей түрде жазуға болады.
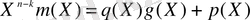(2.4)
мұндағы q(X) және p(X) – бұл бөлімді және полиномды бөлінуден кейінгі
қалдық. Екілік кодтаудағы жағдайдағыдай қалдық жұп сан болады. (2.5)
теңдігін келесідей ұсынуға болады.

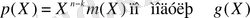(2.5)

U(X) кодтық сөзінің нәтижелік полиномын келесідей жазуға болады.

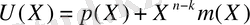(2.6)

(2.5) және (2.6) теңдіктерімен ойластырылған қадамдарды көрсетеміз,
хабарламаны үш сөзбен кодтау арқылы
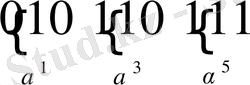
(2.5) кодының көмегімен және генераторы (2.7)
теңдігімен анықталады. Алдымен хабарлама полиномын 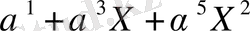– ті
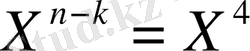–ке көбейтеміз (жоғарға жылжыту), ол мынаны береді 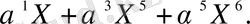Одан
кейін жоғарыға жылжытылған хабарлама полиномын полиномды генераторға
бөлеміз, (1.3.3) теңдігінен 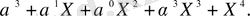Екілік
емес коэффициенттердің полиномды бөлінуі – бұл шаршататын процесс.
Полиномды бөліну нәтижесінде келесідей полиномды қолдықты (полином
ақиқаттығы) беретінін дәлелдеу ретінде алымға қосымша жаттығуды береміз.

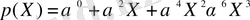(2.8)

(2.5) теңдігінен кодтық сөздің полиномын келесідей үлгіде жазуға болады.
Мәтіндік хабарлама кодының көмегімен систематикалық формада кодталады,
оның нәтижесінде кодтық сөздің полиномы алынады. Хабарлама жіберу кезінде
кодтық сөз бұрмалануға ұшыраған болсын: екі символ қате қабылданған.
(Қателердің мұндай саны қателерді түзетуші кодтың мүмкіндігіне сәйкес
келеді). 7-символдық кодтық сөзді пайдалану кезінде қателік комбинациясын
келесідей полиномды үлгіде көрсетуге болады.

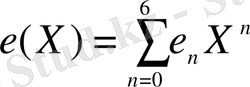(2.9)
Екі символдық қателік мынадай болсын:

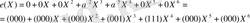(2.10)

Басқаша айтатын болсақ, бақылау символы 1-биттік қателікке бұрмаланған
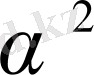( түрінде көрсетілген), ал хабарлама символы 3-биттік қателікке (
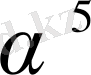түрінде берілген). Бұл жағдайда r(Х) өзгеріске ұшыраған кодтық сөздің
қабылданған полиномы жіберілген кодтық сөздің полиномы мен қателік
комбинациясының полиномының қосындысы түрінде болады, төменде
көрсетілгендей.

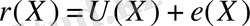(2.11)
(1.5.3) теңдігіне сәйкес (1.5.4) теңдігінен U(X) – ті және (2.12)
теңдігінен e(Х) – пен қосамыз. Және келесіге ие боламыз.

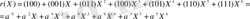(2.13)

Бұл мысалда 2-символдық қатені түзеуде төрт белгісіз айнымалы бар:
екеуі қателердің орналасуына жатады, ал екеуі қателік мағынаға қатысты.
(1.5.4) теңдігінде көрсетілген екілік емес декодтау r(Х) мен екілік кодтау
арасындағы маңызды айырмашылықты көрсетейік. Екілік кодтау кезінде
декодерге тек қана қатенің орналасқан жерін білу керек. Егер қатенің
орналасқан жері анықталса, битті 1– ден 0–ге ауыстыру қажет немесе
керісінше. Бірақ мұнда екілік емес символдар тек қатенің орналасқан жерін
анықтауды талап етіп қоймайды, сонымен бірге символдың осы позициядағы
орналасқан дұрыс мәнінің анықталуын талап етеді. Ал оларды табу үшін теңдік
керек болады.
Синдром дегеніміз – бұл ақиқаттылықты тексеру нәтижесі, ол r – ге
қатысты орындалады және r – дің кодтық сөзге жататындығын анықтау үшін
қажет. Егер r жиынтық мүшесі болып табылса, онда S синдром мәні 0 – ге тең.
Кез келген 0 – ге тең емес S қателердің бар болуын білдіреді. S синдром n-k
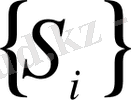
символдарынан тұрады, 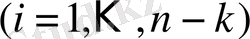. Осылайша, біздің (7, 3) код үшін
синдромның әр векторына төрт симводан келеді; олардың мәндерін қабылданған
r(Х) полиномынан есептеуге болады. Полином түбірі g(X) және де ол g(X)
генерацияланатын кодтық сөздің түбірі болуы керек, себебі дұрыс кодтық сөз
келесідей түрге ие.

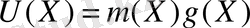(2.14)
Бұл құрылымнан U(X) кодтық сөзінің әрбір дұрыс полиномы g(X) полиномды
генераторға еселi екенін көруге болады. Бұдан шығатыны g(X) түбірлері және
де U(X) түбірлері болуы керек. Себебі 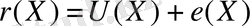, яғни g(X) әр түбірден
есептелетін r(Х) нөлді беру керек, егер де тек r(Х) дұрыс кодтық сөз болса.
Кез келген қателер бір жағдайдың (немесе бірнеше жағдайдың) нәтижесінде нөл
болады. Синдром символдарын есептеуді келесідей жазуға болады.
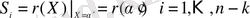(2.15)
мұндағы S – синдром мәні, r(Х) – қабылданған полином. Мұнда r(Х) 2-
символдық қателерден тұрады. Егер r(Х) дұрыс кодтық сөз болып шықса, онда
бұл синдромның барлық символдары нөлге тең болуына алып келеді.
Келесі келтірілген мысалда синдромның төрт символы төмендегідей
орналасады.
(2.16)

(2.17)

(2.18)

(2.19)
Нәтижеден қабылданған кодтық сөз қатеден тұрадынғын көруге болады,
себебі .
Кодтық сөздің позицияларында орналасқан қателері бар
болсын. Онда қателер полиномын келесідей жазуға болады.
(2.20)
1, 2, ..., индекстері 1-ші, 2-ші, ..., -ші қателерді
көрсетеді, ал индексі қателердің орналасуын көрсетеді. Бұрмаланған
кодтық сөзді түзету үшін қателерінің әрбір мәнін және оның
орналасуын (мұнда ) анықтау керек. Қателер локаторының нөмерін
деп белгілейік. Одан кейін синдром символын қабылданған
полиномға қоя отырып есептейміз.
(2.21)
Бізде 2t белгісіз айнымалылары бар (t – қателер мәні және t –
орналасуы) және 2t теңдіктер жүйесі. Дегенмен бұл 2t теңдіктер жүйесін
қарапайым жолмен шешуге болмайды, себебі ондағы теңдіктер сызықтық емес
(кейбір белгісіз айнымалылар дәрежелік теңдікке кіреді). Бұл теңдеулер
жүйесін шешуге мүмкіндік беретін әдістер жиынтығы Рид-Соломон декодталуы
деп аталады.
Егер синдромның нөлдік емес векторы (бір немесе бірнеше символдары
нөлге тең емес) есептелген болса, онда қате қабылданғанын білдіреді. Одан
кейін қатенің (немесе қателердің) орналасуын анықтау керек. Қателер
локаторының полиномын төмендегідей жолмен анықтауға болады.
(2.22)
- тің түбірлері болады. түбірлеріне қарсы шамалар
e(Х) қате комбинациясының орналастырылуларының нөмiрлерiн ұсынады. Онда
авторегрессиялық модельдеу техникасын пайдалана отырып, синдромнан матрица
құрамыз, ол матрицада алғашқы t синдромдар келесi синдромды болжауы үшiн
қолданылады.
(2.23)
Нөл емес анықтауышы бар ең үлкен өлшемді матрицасын алып,
авторегрессиялық модельдеу техникасын қолдандық. Екі символдық қателері
түзетулері бар) коды үшін матрица өлшеміне ие болады, және модель
келесідей үлгіде жазылады.

(2.24)

(2.25)
қателер локаторының полиномының және
коэффициенттерін табу үшін алдымен (1.5.16) теңдігіне кері матрицаны
есептеу қажет. [А] матрицасы үшін кері матрица төмендегідей анықталады.

(2.26)
Демек, det (2.27)

(2.28)
(2.29)

Сенімділікті тексеру. Егер кері матрица дұрыс есептелген болса, онда
бастапқы және кері матрицаның көбейтіндісі бірлік матрицаны беру керек.

(2.30)

(1.5.16) теңдігінің көмегімен қателер лакоторының полиномының
коэффициенттерін есептелулерімен қателерді іздеуді бастаймыз, ол төменде
көрсетілген.

(2.31)

(2.30) және (2.31) теңдіктерінен

(2.32)
түбірлері қателер орналасуына кері сандар болып табылады. Осы
түбірлер табылғаннан кейін қателердің орналасулары белгілі болады.
Негізінде түбірлері жолдың бір ғана немесе біреше элементтері болуы
мүмкін. Бұл түбірлерді барлық элементтері бар полиномды толықтай
тексеру арқылы анықтаймыз (төменде көрсетілген). Кез келген X, элементі
беретін болса, ол түбір болып табылады, бұл қателердің орналасыун
анықтап береді.
(2.32) теңдігінен көрініп тұрғандай, қателердің орналасуы полином
түбірлеріне кері шама болып табылады. Яғни болуы бір түбірдің
алынатындығын білдіреді. Осыдан . Сәйкесінше болуы келесі түбір
алынатындығын білдіреді (мұнда және 1-ші және 2-ші
қателерді білдіреді).
2-символдық қателермен жұмыс істеп жатқандықтан қателер полиномын
төмендегідей жазуға болады.

(2.33)
мұндағы және позицияларында орналасқан екі қате табылды.
Қателердің орналасу нөмерлерін индекстеу кездейсоқ болады. Соныман, бұл
мысалда шамасын және деп белгіледік.
Қателерлі деп белгіледік, мұнда j индексі қатенің орналасуын, ал
l индексі l-ші қатені білдіреді. Себебі әрбір қатенің мәні нақты орналасқан
жерімен байланысты, - ні жай ғана деп белгілеп, белгiлердiң
жүйесiн ықшамдауға болады. Енді және позицияларымен байланысқан
және қате мәндерін анықтауға дайын болғаннан кейін синромның
кезкелген төрт теңдігін қолдануға болады. (2.30) теңдігінен және
- ні аламыз.

2.2 Деректерді тасымалдау кезінде пайда болатын қателер

Көптеген компьютерлік желілерде әртүрлі ұзындықтағы биттердің
үздіксіз кезектілігі түріндегі мәліметтер тасымалы пайдаланылмайды. Желілік
жүйелерде деректер кішігірім блоктарға бөлінеді, бұл блоктарды дестелер деп
атайды, олар бір-бірінен жеке түрде тасымалданады. Сондықтан компьютерлік
желілерді көбінесе дестелік желілер немесе дестелердің коммутациялық
желілері деп атайды.
Дестелерді пайдалану негізінде келесі екі принцип қолданылады.
Біріншіден, беруші мен қабылдаушы компьютерге өздерінің тасымалдау
деректерін қатесіз жіберу үшін іс-әрекеттерін өзара сәйкестендіру.
Тасымалдау кезіндегі қателікте деректер жоғалуы мүмкін. Деректердің
кішігірім блоктарға бөлінуі жіберуші мен қабылдаушыға қай блок зақымдалған,
зақымдалмағанын анықтауға мүмкіндік береді. Екіншіден, байланыс линиялары
және модемдердің сәйкес аппараттық құралдары қымбат болғандықтан, олар
бірнеше компьютерлердің пайдалануына беріледі. Сондықтан желілік жүйе
оларға осы ортаға қатынас жасауға бірдей мүмкіндік беруі қЖелілердіңет.
Мұндай тең құқылы жұмысты іске асыру кішігірім дестелерді қолдану арқылы
ғана қамтамасыздандырылады. Бұған көзіміз жету үшін бұрынғы компьютерлік
желілерде қандай әдістер қолданылғанын қарастырайық.
Алғашқы желілер тең құқылы қатынас жасауға кепілдік беретін.
Қолданбалы бағдарлама белгілі-бір уақытқа байланыстың бөлінетін қорын
иемденетін; қосымшаға басқа қосымша байланыстың осы ресурсын қолдануға
кіріспестен бұрын өз жұмысын аяқтауға рұқсат берілетін. Бұны болғызбас үшін
қазіргі компьютерлік желілерде дестелерді пайдалану қарастырылған. Желі
бір компьютерге бір дестені жіберуге рұқсат береді де компьютерге тосқаул
қояды, сосын басқа компьютерге өз пакетін жіберуге мүмкіндік береді де, осы
компьютерге де тосқаул қойып, келесі компьютерге өз пакетін жіберуге
мүмкіндік береді. Әр компьютер бір дестені жіберуге жетерлік уақытқа ғана
бөлінетін қорды иемденеді, сосын келесі дестені жібермес бұрын басқа
компьютер желіні қолданып болғанша тұрып күтуі тиіс.
Желіге түсетін салмақ – бұл параметр пайызбен өлшенеді.Ол пайыз
мөлшері уақытқа айланысты болады.Яғни желі арқылы мәліметтер қанша уақытта
жіберілетіндігін анықтайды.
Желілердің түрлері сипатына қарай бөлінеді .Жергілікті желі бұл сапалы
байланысты қамтамасыз ететін компьютерлік желі. Локальді жеіге келесі
қасиеттер тән:
1. Ақпаратты тасымалдаудың жоғары жылдамдығы, орташа 100 Мбитс;
2. Тасымалдау қателерінің төмен болуы;
3. Желіге қатынас құру әдісінің жоғарғы жылдамдықта жұмыс ітсеуі,қатынас
құру уақыты 10мс,
4. Желідегі компьютерлердің сандарының шектеулігі.
Байланысты ұйымдастыруда қолданылатын электрондық компоненттер немесе
кабельдерде айбарлы разрядтар, кернеу импульстері мен басқа да
электромагниттік бөгеулер әсерінен керексіз электр токтары туындауы мүмкін.
Күшті бөгеулер (әсіресе, егер олар айбарлы разрядтар нәтижесінде туындайтын
болса) желі құрылғысын зақымдауы мүмкін. Алайда әдетте бөгеулер деректерді
жіберу үшін қолданылатын сигналдарды құрылғыны зақымдамай-ақ, тек
бұрмалайды. Электр сигналының едәуір бұрмалануы бір немесе бірнеше деректер
биттерін қабылдаушымен дұрыс емес интерпретацияны тудыруы мүмкін. Кейбір
жағдайларда бөгеулер сигналды дерлік жойып жібереді, ал бұл жіберуші
мәліметті жібергеннен кейін қабылдаушының деректер түсуін байқамай қалуына
жол береді деген сөз. Кейбір кезде бөгеулер тұрып қалатын тасымал
линиясында мүлдем кері әсер тудыруы мүмкін: жіберуші ештеңе жібермесе де,
қабылдаушы түскен бөгеулерді биттер немесе символдардың мүмкін боларлық
тізбегі сияқты интерпретациялануы мүмкін. Жоғалу, бұрмалану немесе
биттердің еріксіз пайда болуы жалпы атпен тасымалдау қателері деген атпен
танымал және компьютерлік желілердің күрделілігінің негізгі себебі болып
табылады.
Компьютерлік желілер күрделендірудің негізгі себебі тасымалдаудың
цифрлік ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.