Матиматикалық есептер

Пән: Педагогика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

ЖОСПАР.

I. Кіріспе.

II. Негізгі бөлім.

1. Матиматикалық есептер.

2. Есеп шығару және есеп түрлері.

3. Оқушыларды есеп шығаруға үйрету.

III. Қорытынды.

КІРІСПЕ.

Математика ғылым ретінде есептен пайда болған және есеп арқылы дамиды. Тарихқа жүгінсек, ең көне математикалық ескерткіштер Ринд және Мәскеу папирустарында есептер қарастырылып, оларды шығару жолдары берілген. Есеп шығару мұқтаждығынан мүмкіншіліктер теориясы, ойындар теориясы, информатика теориясы т. б. дамыды.

Мектеп математикасын есепсіз құру мүмкін емес.

Ресейдегі алғашқы "Арифметиқа" авторы Л. Ф. Магницкий арифметикалық төрт амалдарды қолдануға арналған есептер жүйесін қүрастырған. "Мақсатты түрде қүрылған есептер әдістемесін" ұсынушы атақгы педагог-математик С. И. Шс&ор-Троцкий үйдің "барлық төрт бұрышына есеп қойылуы керек" деген. Осы кезендегі көрнекті әдіскер-ғалым П. М. Эрдниев: "Барлық әдістеме есеп шығару әдістемесіне шоғырлануы керек", -дейді.

'Математикалық есеп оқушылардың ұғымдарды, теорияны және математика әдістерін меңгерудің тиімді де, айырбасталмайтын қүралы болып табылады. Оқушылардын ойлау қабілеттерін дамытуда, оларды тәрбиелеуде, біліктіліктері мен дағдыларының қалыптасуында, математиканың практикамен байланысын көрсеіуде есептін алатын орны өте зор.

Математиканы оқытудағы басты мақсаттарға жетуге есеп -басты қызметші болып табылады. Сондықтан математика сабақтарының жарты уақыты есеп шығаруға арналады. Әрбір мектеп бітіруші оқушы орта есеппен 15000-дай еcеп шығарады екен. Ал солардың көпшілігі жоғары жөне арнаулы орта оқу орындарыңа түсу емтихандарында математикадан берілген тапсырмаларды шығара алмай жатады. Бүл әлі де мектеп математикасьгн оқытуда есеп шығаруға көңіл аз бөлініп отырғандығьшың дәлелі.

Есептің негізгі міндеттері: оқыту, тәрбиелеу, дамыту және бақылау болып табылады. Барлық есептер оқыту міндетін орындайды. Басқаша айтқанда, кез келген есепті шығарғанда окушы математикалық білім алады, шығару біліктілігі калыптасады, дағдыға ие болады, яғни математикалық білім деңгейі жоғарылаудан. Көбінесе әр есеп өзінің мазмұны арқылы тәрбиелік міндетін атқарады. Мысалы, қоғам дамуының әр түрлі кезеңдеріне байланысты, есеп мазмүны да өзгеріп отырады. Бір кезеңдерде есептер жиңағы көпестердің сауда-саттығын, арзанға сатып алу, керісінше қымбатқа сату, құмарлық ойыңдарында ұту т. с. с. мазмұнды болды. Қазіргі оқулықтарда есеп мазмұңы оқушылардың жоғарғы моральдық қасиеттерін қалыптастыруға, ғылыми көзқарастарын дамытуға, интернационалдық жөне патрисцтық рухта тәрбиелеуге негізделген. Оқушыларды есеп мазмұны арқылы ғана төрбиелеп коймаЦды, оларды есеп шығаруға үйрете тәрбиелеу болып саналады. /Есеп шығару оқушылардың сөйлеу мәдениетіне, мінез-қүлқьшың кдлыптасуына, табандылыққд, шыншылдыққа, бастаған істі аяғына дейін жеткізу, қиындықты жеңе білу сияқгы қасиеттерінің төрбиеленуіне ықпалын тигізетіні аян.

Есеп оқушылардың логикалық ойлау, кеңістікті елестету, жеке"қабілеттерін дамытуға бірден-бір себепші болатын басты құрал болып табылады. Оқушылардың білімін, біліктілігін және дағдысын анықгауды бақылау міндеттері де көбінесе есепке жүктеледі.

§ 2. Есеп шығару және есеп түрлері

Есеп шығару - ерекше жұмыс, дәлірек айтсақ ой жұмысы. Ал кез келген жұмысты дүрыс атқару үшін, оның неден тұратыны және оны орындау үшін қандай құрал, әдіс керек екендігін алдын ала анықтап алу қажет. Кез келген есеп шарттардан және талаптардан құралады.

Есеп: Тікбұрышты үшбұрыштың катеті 5 м-ге тең, ал оның гипотенузадағы проекциясы 3 м. Гипотенузаны жөне екінші катетті тап. Есеп шарттарын былай бөліп көрсетуге болады.

а) Тікбұрышты үшбұрыш; ә) бір катеті 5 м-ге тең; б) белгілі катеттің гипотенузадағы проекциясы 3 м-ге тең. Есеп талабы: а) гипотенузасын және; ә) екінші катетті табу керек. Есеп

шартында ұғымдар, қатыстар, теориялар камтылады. Есеп талабы "дәлелде", "есепте", "сал", "зертте", "қанша болады" т с с. сөздермен айтылады. Есеп шығару дегеніміз не? Мысалдап қарастырайық:

а) а ⁴ +2а ³ ~а ² -2а (1)

көпмүшелігін көбейткіштерге жікте. Шығару:

1) Қосудың ауыстырьшдылық және терімділік заңдар
негізінде берілген (1) көпмүшелігін былай жазуға болады:

а ⁴ +2а ³ -а ² -2а = (а ⁴ +2а ³ ) -(а ² +2а) . (2)

2) Ортақ көбейткішті жақша алдына шығару ереже*
бойынша (2) -ні баскаша жазсақ:

(а ^А + 2а ³ ) -(а ² + 2а) = а\а + 2) -а(а +2) (3)

3) Осы ережені тағы бір қолдансақ, (З) -ден

а ³ (а + 2) -а(а + 2) = а(а + 2) (а ¹ +1)

4) Қысқаша көбейту формуласын пайдалансақ

а{а + 2) {а ² - 1) = а(а + 2) (а -1) (а + 1) .

Сонымен

а ⁴ +2а - а ² -2а = а(а - 1) (а+1) (а + 2) .

Есеп талабына жауап қайтарылды, есеп шығарыдды. ә) Үшбұрыш қабырғалары 13, 14, 15 болса, оған сырттай сызылған шеңбердің радиусын тап.

Шығару: 1) Герон формуласы бойынша

S _∆ = √ p (p-a) (p-b) (p-c)

2) R = abc/4S формуласы бойынша

формуласы бойынша

R = abc / 4 √ p (p-a) (p-b) (p-c)

шығады.

3) Сан мәндерін орнына қойсақ

R = 65/8.

Көрсетілген есептерді шығару кезінде, бүрыннан белгілі қандай да болмасын зандылықтарды есеп шартына қолдана отырып, есептің талабына жауап ізделініп отыр. Яғни,, шығару дегеніміз - математиканың жалпы заңдылыктарын (анықтамалар, аксиомалар, теоремалар, заңдар, формулалар), егеп шартына немесе оның салдарына белгілі бір ретпен қолдана пырып, есеп талабына жауап беру болып табылады. Сонымен есеп шығару, оның шартына белгілі бір математикалық ережелерді сәйкес турде колдана отырып, талабына қарай жылжитын ой қозғалысы. Есеп қарастырылатын объсктілеріне байланысты - практикалык және математикалық болып екіге болінеді. Яғни есепте қарастырылатын объектінің бірі нақты шын зат болатын болса, ол практикалық есеп. Мысалы, Жер радиусы 6370 км, ал одан 4 км жоғары биіктікте үшып бара жатқан тікұшақтан қаншалықты алыс жер көруге болады? Есепте қарастырылатын объектілер таза математикалық болса, ол математикалык есеп. Мысалы, М нүктесінен жүргізілген киюшы шеңберді А жәнеВ нүктелерінде қияды, сол нүктеден жүргізілген жанама шеңберді С нүктесінде жанайды. МС ² = МА х хМВ болатыңдығын дәлелде.

Теоремаға байланысты стандартты және стандартты емес есеп түрлері белгілі. Дайын ережелердің көмегімеи шығарылатын есеп стандарттық есеп делінеді де, ал шығару жолдары дайын ережелер арқылы табыла қоймайтын есеп - стандарттық емес есеп болады. Мысалы. 1 . Егер а=3, d=5 болса, арифметикалық прогрессияның алғашқы алты мүшесін жаз (стандарттық есеп) . 2. Арифметикалық прогрессияның төртікші мүшесі 4-ке тең. Профессия айырымының қандай мәнінде оның алғашқы үш мүшесінің қос-қостан алған көбейтінділерінің косындысы ең кіші манге ие болады (стандартты емес) ? Есеп талабына қарай: а) есептеу, ә) дәлелдеу, б) зерттеу, в) салу есептеріне бөлінеді. Есептеуге арналған есептерге: өрнек мәнін табу, функцияның мәнін есептеу, кесіндінін үзындығын, фигураның ауданын табу, бүрыш шамасын аныктау т. с. с. жатады.

Қандай да болмасын ұйғарымның ақиқаттылығына көз жеткізу немесе ұйғарымның жалғандығын тексеру не белгілі бір құбылыстың дұрыстығын түсіндіру - дәлелдеу есептері.

Теоремалардың барлығын да дәлелдеу есептеріне жатқызуға болады.

«2 ¹⁷ + 1 саны жай сан ба, құрама сан ба?»

«Қандай трапецияның диагоналы оның орта сызығын тең үш бөлікке бөледі». «а және ь-ның қандай мәндерінде

a/b=0, a/b=1, a/b=-1, ab›1, a/b›1, a/b›-1

теңдіктері орынды» т. с. с. есептері зерттеуге арналған есетер. Зерттеу көптеген есептер шығару кезінде кездеседі: нүктелердің геометриялық орны, теңдеулер мен теңсіздіктердің сандарының қаншалықты болды т. с. с.

Белгілі бір құралдар жәрдемімен берілген шарттарды қанағаттандыратын фигуралар салу - салу есептерін құрайды. Есеп шығаруға кіріспес бұрын, оқушыларды есеп түріц анықтап алуға үйрету - басты талаптардың' бірі больщ табылады.

Өзінің алға қойған дидактикалық мақсаттарына қарай есептерді үш түрге бөлуге болады:

1) танымдық есептер: бүлар арқылы жаңа білім алынады; 2) машықтану есептері: бүлар арқылы орнықты білім дағдылар қалыптасады; 3) шығармашылық ойлауды қажет ететін дамыту есептері. Таным есептерін жаңа материалдар өтуде, оқытудың проблемалық және эвристикалық әдістерін қолдануда шығару керек. Бұл дидактика талаптарына сай келеді, сондықтан математиканы оқып-үйрену барысында кеңінен қолданыладк. Алайда мектеп математикасында ең көп тараған есеп түрлері жаттығу есептері болып табылады, олар математикалық білімдерді қолдануда сапалы және берік дағдылар қалыптастыра отырып, математикалық теорияларды саналы түрде меңгеруге ықпал етеді.

Жаттығу және танымдық есептерді шығарумен шектелу, оқушылардың эвристикалық, шығармашылық ойлауын дамытуды толық қамтамасыз ете алмайды. Сондықтан бұл мақсатты жүзеге асыруға математикалық, логикалық, интуициялық, тапқырлық т. б. қабілеттер араласатын арнайы іріқтелген есептер шығарып отырудың маңызы аса зор.

Шешу кезінде қандай ойлау түрінің басым болуына байланысты есептерді алгоритмдік, жартылай алгоритмдік және эвристикалық деп шартты түрде үшке бөлуге болады. Танымдық есептер негізінен жартылай алгоритмдік, дамытушы-эвристикалық есептерге жатады. Формула немесе ереже бойынша шығарылатын есептер алгоритмдік және жартылай алгоритмдік болып келеді.

Есеп шығаруға төмендегідей талаптар қойылады:

а) Қатесіз шыгару; ә) негіздеу (дәлелдеу) ; б) толық шыгару; в)

мумкіндігінше тиімді жолмен шығару; г) есепті қаттау

(оформление) .

а) «Есеп қатесіз шығарылу керек».

Бұл негізгі талап. Оқушылар есеп шығару кезінде алгоритмдік, логикалық, сызбалық, терминологиялық, шындықты бұрмалау сияқты қателер жіберуі мүмкін. Енді оқушылар жиі жіберетін қателіктерді көрсетелік.

1/2+1/3. =2/5

(а + b) ² =а ² +b ² - алгоритмдік қатерліктер

sіп(ά+β) ² = sіп ² ά+ sіп ² β

√(a+b) = √ a+√b

5=-5 екендігін дөледдеу. Екі жағын квадраттаймыз, соңда 25=25

Немесе

1/a=a

a=1/a

1/a*a=a*1/a

1 = 1- логикалық қателік.

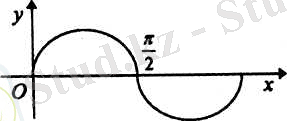
Бүйір жақтары квадраттар болатын алты бұрышты дұрыс призманың ішінен төменгі табанының қабырғасы мен жоғарғы табанының оған қарсы жатқан қабырғасы арқылы жазықтық жүргізіңдер. Осы қима тіктөртбұрыш ретінде салынса, ол сызбалық қате. Суреттегі cинусоида да сызбалық қате .

«Бүйір жағының апофемасы», «шеңбердің ауданы» т. с. с. - терминологиялық қателіктер.

Есеп: «Моторлы қайық өзен ағысымен 42 км және ағысқа Қарсы 20 км жол жүріп және оған 5 сағ уақыт жұмсады. Егер өзен ағысының жылдамдығы 2 км/сағ болса, қайықтың өз жылдамдығы қаңдай?».

Есеп 42/(x+2) +20/(x-2) тендеуін құру арқылы шығарылады.

Теңдеу түбірлері 2/5 және 12 есеп жауабы ретінде алынса, онда

шындындықты бұрмалау қателігі жіберілгені.

§ 4. Оқушыларды есеп шығаруға үйрету

Әрбір есеп белгілі бір немесе бірнеше дидактикалық мақсаттарға жету үшін берілетіндігі түсінікті. Есеп дидактикалық мақсаты мен мазмұнына байланысты математикалық ұғымдарды қалыптастыруға, символикаларды меңгеруге, дәлелдеуге үйретуге, білім және біліктілікті қалыптастыруға, ойлау қабілеттерін арттыруға т. б. арналуы мүмкін. Оқытушы есеп шығарудың әр түрлі өдістерін (анализ және синтез, байқау арқьшы танысу, жинақтау, модель құру т б. ) жүйелі түрде үйретуі керек. Есеп шығару қандай максатқа бағытталса да мүғалімнің басты міндеті оқушылардың есеп шығару төжірибесін молайту, оларды есеп шығаруға үйрету болуы тиіс. Әрине, бүдан мұғалім оқушыға шамадан тыс көмектесуі керек деген қорьггынды шыяаруға болмайды. Мүндай жағдайда оқушыға жүмыстың аз үлесі тиеді де, есеп шығару тәжірибесін молайта алмайды. Керісінше, мүғалім көмегі өте аз болса, оқушы есеп шығаруға мүлдем үйрене алмайды.

Мүғалім сұрақ-жауап арқылы ақыл-кеңес бере отырып, оқушыны есеп шығарудың әр қилы сырына үйрете алады. Әр түрлі есептерді оқушыға үйрету үшін сұрақтар мен акыкенестер жалпылама сипатқа ие болу керек. Есеп шығара білу-қыры мен сыры мол, үзіліссіз тәжірибе арқылы келетін үлкен өнер екенін есте үстау қажет. Есеп шығаруға бағыт, бағдар беретін ғылыми-әдістемелік әдебиеттерге (Колягин Ю. М., 0ойа Д. Туманов С. И., Фридман Л. М., Эрдниев П. М., Эсаулов д. Ф. т. б. ) шолу жасай отырып, озық тәжірибелі мұғалімдердің еңбектеріне сүйене келе, қандай да болмасын есепті шығаруды негізгі төрт кезеңге бөлуге болады:

есептің шарты мен талабын терең түсіну;
есепті шығарудың жоспарын қүру;
жоспарды жүзеге асыру;
есепті тиянақгау.

Көрсетілген кезеңдерге байланысты негізгі мәселелер
төңірегінде кеңес берелік.

Есепті дүрыс түсініп алмай, оны әрі қарай жалғастыру мүмкін емес. Есеп шығаруға сығудың керегі жоқ. Шығаруға кіріспес бүрын оның мазмұнына талдау жасап не берілгенін, нені іздеу керек екендігін анықтау керек. Бүл түста үқыпты сызылған сызба немесе сүлбелердің көмегі зор. Егер есептің берілген немесе ізделінді элементтері белгіленбеген болса, онда ыңғайлы белгілеулер енгізу керек. Есеп бір жакты аныкталмаған ба, соны тексеру қажет. Мүмкіндігінше есеп шартында артық мәселелер, қайшылықтар бар ма, солардм тиянақты түрде анықгау керек.
Есеп шығарудың жоспарын құру, щешуші кезең болып табылады. Есеп шығарудың жоспары дұрыс құрылғанда ғана, есеп қатесіз шығарылады. Жоспар қүру үзақ және күрделі болуы мүмкін. Сондыктан, оқушыға есеп шығарудың негізгі «кілтін» ұсынатын идеяларға байланысты сұрақтар мен ақыл кеңестер жүйелі түрде құралғаны орынды:

а) Осы сияқгы есеп бұрын кездесті ме? Ол жағдайда қалай еді, тығарылатын есепте қалай? Егер шығарылмайтын есепке үқсас еееп бұрын-сонды кездескен болса, онда есеп жоспарын құру
онша қиындық келтірмейді. Көбінесе берілген есепке жақын есеп кездесе бермейді. Бұл жағдайда:

ә) Шығарылатын есепке ұқсастау, соған келтіруге болатындай есепті ойластыр. Ондай есеп табыла қалса, онда есеп жоспарын құру да жеңілдейді. (Берілген есепті шығару жолын бұрыннан белгілі есепке келтіру жеткілікті. )

б) Есепке жақындайтын бұрыннан белгілі есеп табылмаса ше? Бүндай жағдайда: «Есепті басқаша оқы» деген кеңес берілуі мүмкін. Яғни, есептің шарғандағы үғымдардың анықтамасын пайдалану, оның қасиеттерін еске алу немесе есеп шарты мен талабын математикалықтілге көшіру қажет болады (бұл жағдай мәселе есептер шығару кезінде кездеседі) .

в) Жоспар құру кезінде: «Есептің берілгендерінің барлығын дерлік қолданылды ма?» деген сұрау жиі-жиі қойыльіп отырылғаны жөн.

г) «Есеп шарты мен ізделіндісін түрлендіруге тырыс» дегең кеңес те көп пайдасын тигізеді. Есеп шарты немесе талабьің түрлендіру, «тонын айналдыру» есеп жоспарын қүруд _ы тездетудің бірден-бір кепілі. Тепе-тең түрлендіру есептіңі берілгені арқылы оның белгісізіне жетуге жол ашады. Мысалы тендеулер (теңсіздіктер) немесе олардың жүйесін шешкенде' мәндес тендеулер (теңсіздіктер) немесе олардың жүйесіне көшу шешімдерін табуға көп жеңілдік жасайды.

д) Есеп жоспарын қүру тіптен қиындап бара жатса, тағы бір кеңес көмектесуі мүмкін: «Есептің бір бөлігін ғана шығаруға тырыс». Мысалы, «Берілген радиусы бойынша, берілген түзу мен шеңберге жанасатын шеңбер сыз». Әуелі берілген түзумен немесе берілген шеңбермен ғана жанасатын шеңбер салу жоспарын жасап алып, екі шешімді біріктіре отырып, берілген есепті шығару жоспарын құруға болады. Бұдан есепті жай, қарапайым есептерге бөліп алып қарастыру да көп жеңілдік тудыратындығы туындалады.

е) Кей жағдайда есегтті қарапайым жағдай үшін шығару жолын тауып алып, оны жалпы жағдайға ауыстыру мүмкіндігің ойластырған жөн.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.