Ауаның адиабата көрсеткішін табу жолдары

Кіріспе

1. Теориялық бөлім
1.1 Адиабаталық процесс. Пуассон теңдеуі.
1.2 Жылусыйымдылық
1.3 Термодинамиканың бірінші бастамасын изопроцестерге қолдану

2. Практикалық бөлім
2.1 Қондырғы сипаты
2.2 Жұмыстың орындалу реті

Салыстырмалы бөлім

Қорытынды

Қосымша мәліметтер

Қолданылған әдебиеттер тізімі

Осы жұмыста қарастырылатын мәселе молекулалық физика құбылысының бір түрін зерттеу әдісімен танысып, формулаларды түрлендірулер туралы болмақ. Бұл жұмыс өзіне өте ауқымды мәліметтерді жинақтай отырып, көптеген құбылыстарға сипаттама беріп отыр. Сіздер бұл жұмысты оқу барысында ауаның адиабата көрсеткішін табу жолдарын қарастыратын боласыздар. Сонымен қатар, ауаның адиабата көрсеткішін практика жүзінде дәлелдеп, сызбалар арқылы өрнектелгеніне көз жеткізесіздер.
Жұмыстың мақсаты: Изопроцестер заңдылықтарымен танысу және тұрақты қысым мен тұрақты көлем кезіндегі ауа жылу сыйымдылытарының қатынасын анықтау.
Жұмыстың міндеті:
1. Адиабаталық процеске анықтама беру
2. Термодинамиканың екінші бастамасын изопроцестерге қолдану
3. Қондырғының сипатын анықтау
4. Жұмыстың орындалу ретін құру

1. Кикоин А.К. Кикоин И.К. Молекулярная физика. – М.: Наука, 1976.
2. Гершензон Е.Н. Малов Н.Н. МансуровА.Н. Эткин В.С. Курс общей физики: Молекулярная физика. – М.: Просвешение, 1982
3. Фриш С.Э. Тиморева А.В Курс общей физики.
4. Зисман Г.А. Тодес О.М. Курс общей физики – Т.1. – Наука, 1970.
5. Кудрявцев В.Б Курс физики: Теплотип и молекулярная физика.
6. Практикум по общей физике / под ред. В.Ф. ноздрева, - М.: Наука, 1976.
7. Матвеев А.Н. Молекулярная физика. – М.: Высшая школа, 1987.
8. Баскаков А.П. Теплотехника. – М.: Молекулярная физика. 1991.
9. Кравцов Ю.А. Мансурав А.Н. и др. Лабораторный практикум по общей физике. – М.: Просвещение, 1985.
10. Корзун И.Н. Лабораторные работы по механике и молекулярной физике. – Алматы: Қазақ университеті, 1991.
11. Қойшыбаев Н. Молекулалық физика. ІІ –Том. Оқулық. – Алматы: “Зият Пресс”, 2005. – 228б.

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

1 Кіріспе

Осы курстық жұмыста қарастырылатын мәселе молекулалық физика құбылысының
бір түрін зерттеу әдісімен танысып, формулаларды түрлендірулер туралы
болмақ. Бұл жұмыс өзіне өте ауқымды мәліметтерді жинақтай отырып, көптеген
құбылыстарға сипаттама беріп отыр. Сіздер бұл жұмысты оқу барысында ауаның
адиабата көрсеткішін табу жолдарын қарастыратын боласыздар. Сонымен қатар,
ауаның адиабата көрсеткішін практика жүзінде дәлелдеп, сызбалар арқылы
өрнектелгеніне көз жеткізесіздер.

Жұмыстың мақсаты: Изопроцестер заңдылықтарымен танысу және тұрақты қысым
мен тұрақты көлем кезіндегі ауа жылу сыйымдылытарының қатынасын анықтау.

Жұмыстың міндеті:
1. Адиабаталық процеске анықтама беру
2. Термодинамиканың екінші бастамасын изопроцестерге қолдану
3. Қондырғының сипатын анықтау
4. Жұмыстың орындалу ретін құру

1. Теориялық бөлім

1. Адиабаталық процесс. Пуассон теңдеуі.
1) Сыртқы ортамен жылу алмаспайтын процесс Адиабаталық процесс деп
аталады. Газдың квазистаттық адиабаталық процесс жасаған кездегі идеал
газдың күйін анықтайтын өзара параметрлерді қарастырайық.

, алатынымыз

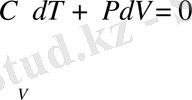
Менделеев – Клапейрон теңдеуінен

қысқартып, аламыз

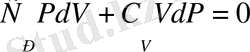
Анықтама енгіземіз
γ
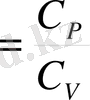(1)
Сонда

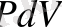
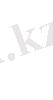(2)
Квазистатика адиабаталық процесс идеал газ үшін осы дифференциалданған
өрнекке тең.
Идеал газдың 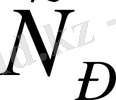және жылусыйымдылықтары температураға тәуелді.
Бірақ көп жағдайда олар тұрақты болып қалады. Егер олай болса, олардың
қатынасы да тең болады. Сонда (2) теңдеуін оңай интегралдап алатынымыз.

(3)
Бұл теңдеу Пуассон теңдеуі деп аталады (1781-1840). Бұл өрнек адиабата
теңдеуі болып табылады, яғни қисық, кестелік квазистатикалық өрнек адиабата
процесін сипаттайды. Шамалы адиабаталық тұрақтылық болып табылады. Егер
деп алсақ, адиабата өрнегін тағы екі түрде жазуға болады.

(4)

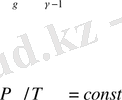(5)
Егер γ1 деп алсақ, онда (4) өрнегінен адиабаталық сығылу кезінде газ
қызатынын, ал адиабаталық ұлғаю кезінде газ суыйтынын байқауға болады.
Газдың қызуы адиабаталық сығылу кезінде, газдың сығылуға жұмсалатын
жұмыспен анықталады, ол ішкі энергияның өзгеруіне әкеледі.
Идеал газдың ішкі энергиясы температурадан тәуелді, яғни ішкі энергияның
артуы температураның ұлғаюымен анықталады.
2) 3 – 5 адиабата теңдеулері тек квазистатикалық адиабаталық процеске
жатады. Ал квазистатикалық емес адиабаталық процестер үшін бұл өрнектер
қоланылмайды. Мысалға, қарастырайық, адиабаталық жабық цилиндр тең екі
бөлікке бөлінген. Ал газ осы екі бөліктің бірін алсын дейік. Егер
ортасындағы бөлікті ашсақ, онда газдың адиабаталық ұлғаюы болады. Бұл
процесс квазистатикалық емес. Бастапқыда күрт теңгерілмеген күй болады,
газдың макроскопиялық күрделі әрі жеңіл жетелеуі болады. Одан кейін осы
макроскопиялық қозғалыстар өшеді, яғни ішкі үйкеліс кезінде, олардың
кинетикалық энергиясы ішкі энергияға айналады. Процесс соңында күйлер
теңеледі. Осы кезде газ барлық көлемді алады. Ол тұрақты тығыздық пен
температурада ғана жүзеге аспақ. Процесс кезінде газ ешқандай жұмыс жасаған
жоқ. Жылу денеге берілмеді, өйткені ішкі энергия өзгеріссіз қалады. Осыдан
Джоуль заңына сәйкес қорытындыласақ, процесс кезінде температура тұрақты
болып қалатынында. Қателік болар еді егер де адиабата теңдеуіне газдың
бастапқы және соңғы күйін қолдансақ[4]. Егер солай жасаған жағдайда біз
қате қорытынды жасаған болар едік, яғни адиабаталық процесс кезінде газ
сууы керек.
Әдетте, егер бастамасы теңсіздіктен үлкен болмаса, онда адиабата
көрсеткішін тең емес процестерге қолдануға болар еді. Бұндай шарт
орындалады, мысалы, Клеман мен Дезорм әдісінде адиабата көрсеткішін анықтау
кезінде, сонымен қоса қарапайым дыбыстың толқын кезінде газдар да таралады.

Газдың адиабаттық ұлғаюы

1 – суретте (АС қисығы) идеалдың газ квазистатикалық (өте баяу)
адиабаталық ұлғаюы көрсетілген. Ол изотермиялық процесті сипаттайтын
қисыққа қарағанда тіктеу, бұл дегеніміз көлемнің бірдей өзгерісі кезінде
адиабаталық ұлғаю үшін қысымның өзгерісі көбірек болады дегенді білдіреді.
Демек, адиабаттық ұлғаю процесі кезінде газ температурасы төмендейді.
Керісіеше, адиабаттық сығылу кезінде газ температурасы ұлғаяды.

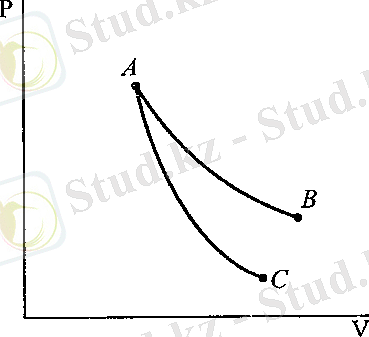
1 – сурет
Адиабаттық түрде баяу ұлғаятын идеал газдың Р қысымы мен V көлемі
арасындағы қатынасты табуға болады. Оны дифференциалдық түрде жазылған
термодинамиканың бірінші бастамасын қарастырудан бастайық:
;
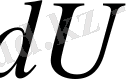бұл жерде біз адиабаттық процесс үшін 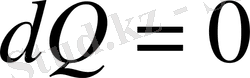болатындығын ескердік.
өрнекті дифференциалдық түрде жазып
,
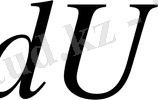осы екі өрнекті біріктіріп, мына теңдеуге келеміз:
.
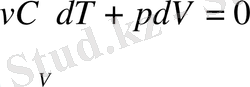Енді идеал газдың күй теңдеуін p, V және T шамаларын өзгереді деп
алып, дифференциалдаймыз:
.
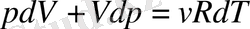Осы теңдеуден дифференциалын тауып, оны жоғарғы теңдеуге қоямыз:
.
теңдікті пайдалансақ, онда:

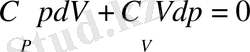
Енді адиабата көрсеткішін енгізіп, соңғы теңдікті мына түрге
келтіруге болады:
.
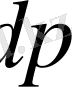Осы теңдеуді интегралдап,
,
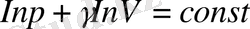немесе,

(6)
деп жазамыз. Соңғы теңдеу Пуассон теңдеуі деп аталады. Бір атомды газдар
үшін (мысалы, Ne, He т.б.) і=3, =1,67; ал екі атомды газдар үшін
(мысалы, Н2,О2,N2 және т.б.) і=5, =1,4; үш және одан көп атомды газдар
үшін (СО2,Н2О және т.б.) і=6, =1,3 болып, (1) формуламен есептелген
-нің теориялық мәндері эксперименттің нәтижиелерімен сәйкес келеді.
Адиабаталық процестерін 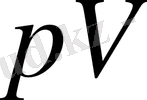координаттарындағы диаграммасы гипербола
қисығымен кескінделеді (2 – сурет). Сонымен адиабата қисығының теңдеуі

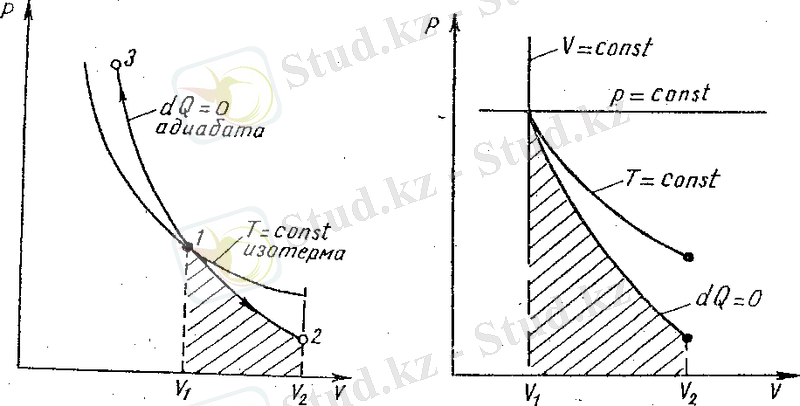
2 – сурет
3 – сурет
болса, изотерма қисығына қарағанда тіктеу екенін көреміз. Мұның
себебі адиабаталық сығылу кезінде оның қысымы изотермалық сығылуға сәйкес
өседі, сонымен қатар оның температурасы да артады. Ал, енді адиабаталық
ұлғаю кезінде газдың температурасы төмендейді, сондықтан газдың қысымы
изотермалық ұлғаюға қарағанда өте тез кемиді. Олай болса, адиабаталық ұлғаю
кезіндегі газдың бір молінің істеген жұмысы штрихталған ауданмен
кескінделеді
(7)
мұндағы
Енді 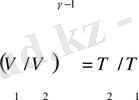қатынасын ескеріп, (14) теңдеуі мына түрде жазуға болады:

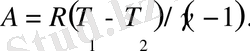
берілген газ күйінің -ден басқа 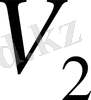-ге ұлғаюы кезінде істелген
адиабаталық жұмыс, изотермалық жұмысқа қарағанда кем екенін байқаймыз (2 –
сурет, изотерма қисығы жоғары орналасқан). Адиабаталық процесс кезінде газ
суынып, температурасы төмендесе, изотермалық процесс кезінде, керісінше,
тұрақты температураны термостаттан келетін жылу мөлшері әсерінен ұстап
тұрады. Сондықтан изотермалық процесс кезінде газ көлемінің ұлғаюы мен
тығыздығының кемуінің салдарынан оның қисымы да азаяды, ал адиабаталық
процесте, керісінше, газ тығыздығы азайған сайын оның орташа кинетикалық
энергиясы кемиді, яғни температурасы төмендейді.
Енді жоғарыда қарастырылған изопроцестер мен адиабаталық процестің
диограммасын салыстырып көрелік (3 – сурет). Суретте көрсетілгендей,
изохоралық процесс диограмма қисығының теңдеуі болса, онда изобаралық
процесс үшін изотермалық процесс үшін ал адиабаталық процестің
болу шарты

2. Жылусыйымдылық

Дененің температурасын бір кельвинге арттыру үшін оған берілетін жылу
мөлшеріне тең шама дененің жылу сыйымдылығы деп аталады. Егер денеге
берілген жылу мөлшері оның температурасын шамасына арттыратын болса,
онда анықтама бойынша, жылу сыйымдылық

(8)
Бұл шама кельвинге бөлінген джоулдермен өлшенеді (ДжК).
Жылусыйымдылық екіге бөлінеді: меншікті және молярлық.
Заттың меншікті жылусыйымдылығы деп 1 кг заттың температурасын 1 К-ға
қыздыру үшін қажетті жылу мөлшерінің шамасын айтады.
Молярлық жылусыйымдылығы деп 1 моль заттың температурасын 1К-ға қыздыру
үшін қажетті жылу мөлшерінің шамасын айтады. Жылусыйымдылығының өлшем
бірлігі: Дж(кгК), Дж(мольК), Дж(м3К), ал оның жүйеден тыс өлшеу бірлігі:
кал(мольК).
Бір ғана заттың мольдік және меншікті жылу сыйымдылықтарының арасында
мынандай қатынас бар:

(9)
(М – молдік масса).
Жылу сыйымдылықтың мөлшері дененің қандай жағдайларда қыздырылғанына
тәуелді.
Тұрақты көлем кезіндегі жылу сыйымдылық (CV). Егер дене тұрақты көлем
кезінде қыздырылған болса, дене сырт денелерге қатысты жұмыс атқармайды
және

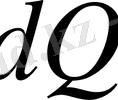(10)
болады. Осыдан

(11)
Мұндай жазу V тұрақты кездегі дифференциалдау дегенді білдіреді. Идеал
газ жағдайындағы U тек T температураға ғана тәуелді болатындықтан, (11)
өрнекті төмендегіше жазуға болады:

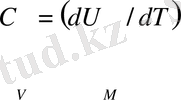
(мольдік жылу сыйымдылықты алу үшін газдың бір молінің ішкі энергиясын алу
керек.)
(9) өрнек газдың бір молі үшін түрінде келеді. Оны Т бойынша
дифференциалдасақ, 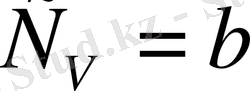болады. Сонымен, идеал газдың ішкі энергиясы үшін
өрнекті

(12)
түрінде жазуға болады, - мұндағы газдың тұрақты көлем кезіндегі жылу
сыйымдылығы.
Газдардың жылу сыйымдылығы қатты денелер мен сұйықтарға қарағанда газдың
қандай процеске қатысатындығына күштірек тәуелді болады. Газдар үшін аса
маңызды екі процесс бар, олар – көлем немесе қысым тұрақты болып қалатын
процесс.
Газдар үшін молдік жылу сыйымдылықпен қатар жылу
сыйымдылықты да енгізу керек. Сонда газдың v молін кельвинге
қыздыруға қажетті жылу мөлшері былай жазылады:
,
(12 а)
.
(12 б)
Мұндағы молдік жылу сыйымдылықтар мен меншікті жылу сыйымдылықтар
арасындағы байланыстар мынандай:
, ,
М – газдың молдік массасы.
(8) және формулаларынан шығарсақ:

Егер
,
онда

(13)
Көлем V температурадан Т ғана тәуелді емес, қысымнан да Р, 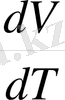өрнегі
қысымның өзгеруіне байланысты түрлі мәндерді қабылдайды.
(2) өрнекке мән беру үшін, осы өрнектің мәнін ескеру қажет. Басқа сөзбен
айтқанда бағытын өрнектеу керек, яғни жүйенің жақын күйге ауысуын
қадағалау керек. Ал бұл бағыт әр түрлі болуы мүмкін, С жылусыйымдылық
қалаған мәнге ие бола алады, -∞ тен +∞ дейін Изотермиялық процесс үшін
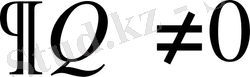, ал бұл жағдайда , . Адиабаталық процесс үшін , .
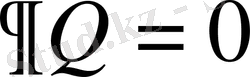Жылусыйымдылық негізгі мағынаны тұрақты көлем мен тұрақты қысым кезінде
қабылдайды. Оларды және деп белгілейміз.
Егер көлем тұрақты болса, онда және келесі

(14)
Егер тұрақты қысым болса, онда өрнегі өрнегіне ауысады. Бұл
жағдайда өрнек (2) береді.

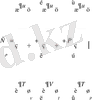(15)
Екеуінің айырымы үшін аламыз

(16)
Тұрақты қысым кезіндегі жылу сыйымдылық ()
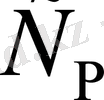өрнегі үшін келесі түрде жазуға болады. Егер процесс тұрақты
қысым кезінде ақса, онда энтальпия анықтамасы бойынша . Сондықтан

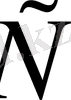(17)

3. Термодинамиканың бірінші бастамасын изопроцестерге қолдану

Газдың күшін сипаттайтын үш параметрдің (р, V, T) процесс кезінде әйтеуір
біреуі тұрақты болып отырса, онда мұндай процестерді изопроцестер деп
атайды. Олай болса, термодинамиканың көптеген мысалдарында: жылу
қозғалтқыштарының жұмысын есептеуге, суыту машиналарының жұмысы кезінде,
қысқасы газдардағы процестер туралы көбірек айтуға болады.
1.Изохоралық процесс деп, берілген газдың көлемі (V=const) тұрақты
болғанда жүретін процесті айтамыз. Сонда ешқандай көлем өзгерісі болмайды
да (dV=0) газ сыртқы күштерге қарсы жұмыс жасайды:
dA=pdV
Осы (1) процестің диаграммасын былайша кескіндеуге болады (4 – сурет).
Мұндағы 1 – 2 газдың изохоралық қыздыру процесін, ал 1 – 3 газдың
изохоралық суыну процесін көрсетеді.
Әдетте изохоралық процесс көлемі өзгермейтін, қабырғалары қалың ыдыстың
ішінде газды суыту немесе қыздыру арқылы орындалады. Термодинамиканың
бірінші бастамасы бойынша dQ=dU+dA, dA=0 болғандықтан, газды қыздыруға
немесе суытуға берілген барлық жылу мөлшері тек газдың ішкі энергиясын
арттыру үшін ғана жұмсалады:
dQ=dU.
(18)
Ал тұрақты көлемдегі жылу сыйымдылық: Сv=
dU=mCv dT,
(19 )
яғни идеал газдың ішкі энергиясының өзгерісі оның абсолют температурасының
өзгерісіне тура пропорционал болады.
2.Изобаралық процесс. Бұл процесс берілген газдың қысымы (р=const)
тұрақты болғанда жүреді. Оның диограммасын p – V координаттары арқылы
кескіндеп көрсетуге болады (5 – сурет). Сонда 1 – 2 кесіндісі газдың

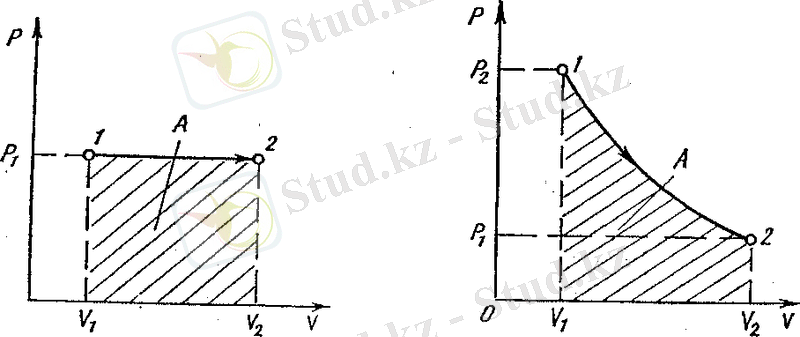
4 – сурет
5 – сурет
изобаралық ұлғайуын көрсетеді де, штрихталған аудан изобаралық жұмыстың
шамасын анықтайды:
A=pdV=p(V2 – V1).
(20)
Мысалы, цилиндрдің ішінде ілгерілемелі еркін қозғалатын прошень мен
цилиндрдің арасындағы газ қыздырудың немесе суынудың нәтижиесінде
изобаралық қозғалыс жасайды. Термодинамиканың бірінші бастамасын ескеріп:
dQ=Сv dT+pdV,
(21)
мұндағы Сv – изобаралық жылу сыйымдылығы. Сонымен, изобаралық процесс
кезінде газға берілген жылу мөлшері оның ішкі энергиясын арттыруға және
сыртқы күштерге қарсы істелген жұмысқа ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.