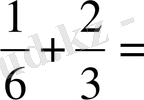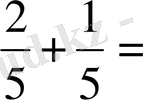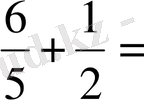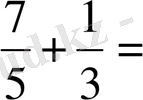Нақты сандар

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 23 бет
Таңдаулыға:

ЖОСПАР

КІРІСПЕ

І. Тарау БАСТАУЫШ МЕКТЕП МАТЕМАТИКАСЫНДА НАҚТЫ САНДАРДЫ ОҚЫТУ

1. 1. Оң рационал сандар

ІІ. БАСТАУЫШ МЕКТЕПТЕ ОНДЫҚ БӨЛШЕКТЕРДІ ОҚЫТУ ӘДІСТЕМЕСІ.

2. 1 Ондық бөлшектердің анықтамасы.

2. 3. Ондық бөлшектерді жай бөлшектерге түрлендіру.

2. 4. Ондық бөлшектерді салыстыру.

2. 5. Ондық бөлшектерге амалдар қолдануды деңгейлеп оқыту.

ҚОРЫТЫНДЫ

ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР

Кіріспе

Зерттеудің көкейкестігі.

Математикада сан ұғымы фундаменталды ұғымдардың бірі. Адам сан ұғымының көмегімен нақты өмірдің сандық қатынасын таниды. Нақты сандар адамзаттың қажетінен пайда болған. Ең алғашқы сандар туралы оқулық әл-Хорезмидің "Арифметикасы"болды. Бұл кітап XII ғасырда латын тіліне аударылды, осының арқасында еуропалықтар ондық позициялық принціппен танысты. Осы уақыттан бастап, біртіндеп араб цифрларына және жаңа есептеу жүйелеріне өте бастады.

Сан ұғымы тас дәуірінде пайда болғанмен, математикалық теория ретінде тек ХІХ ғасырдың екінші жартсында қалыптасты.

Менің курстық жұмысым екі тараудан тұрады. Кіріспеде жұмыстың көкейкестілігін, мақсатын және міндеттерін келтірдім. Екінші тарауында рационал сан теориясының мазмұнын: рационал сан ұғымының шығу тарихы; рационал сан ұғымын жиындар теориясы тұрғысында беру; сандардың аксиомалары . Екінші тарауында бастауыш мектепте нақты сандарды ондық оқыту әдістемесі және ондық бөлшектерді деңгейлеп оқыту әдістемесін келтірдім, сандарды оқыту барысында мұғалімге қойылатын талаптарды құрдым.

Математиканы оқыту әдістемесінен, оның ішінде математика сабағында жаңа технологияларды қолдану туралы әдебиеттер жоқтың қасы. Сондықтан да курстық жұмысымның “Нақты сандар” тақырыбы көкейкесті деп ойлаймын.

І ТАРАУ. МЕКТЕП МАТЕМАТИКА НАҚТЫ САНДАРДЫ ОҚЫТУ

Мектеп математика курсында рационал сандарды оқыту әдітемесі.

Оң және теріс сандар. Бағдарлама бойынша І - VI сыныптын математика курсында негізгі тақырып - сандар. Сондықтан мұғалімнің негізгі мақсаты окушылар сан ұғымын жақсы түсініп олармен қателіксіз амалдар орындай біліп, ауызша және жазбаша есептеу жұыстарын ұтымды түрде орындауға үйрету керек. Оқушылар V сыныпқа келгенде натурал сандарды, нольді, жай және оңдық бөлшектермен арифметикалық амалдарды орындайды және салыстыруды біледі.

« Оң және теріс сандар » тарауы бағдарлама бойынша төмендегідей ретпен оқытылады:

1 Бағыт және сандар . Бұрыннан белгілі сандар түзудегі нүктелерді толық қамтамасыз ете алмайтындығы анықталады. Координаттық түзу енгізіледі. Ноль нүктесінін оң және сол жағындағы нүктелерді белгілеу үшін оң және теріс сандар енгізіледі. Кейін, сандық түзудін бойындағы нүктелердің координаталарының ұғымы, қарама-қарсы сандар, санның модулі және координаттық жазықтық енгізіледі. Оң және теріс сандар жиынында салыстыру амалы қарастырылады.

2. Қосу және азайту . Екі қарама-қарсы бағытта өзгере алатын шамалар қарастырылады. Әрбір осындай шаманың мәнінің өсуін оң санмен, кемуін теріс санмен сипаттауға келісеміз. Тіркес тұрған a шамасының b -ға өсуінің сипаттамасы ретінде кез келген a және b сандарының косындысының ұғымын енгіземіз. Осыдан индуктивті түрде сандарды косудың сәйкес ережелері шығады. Қосудың ауыстырымдылық және терімділіқ зандарының орындалатыны тәжирібе арқылы тексеріледі. Теріс сандарды азайтудың мағынасы бұрыннан белгілі оң сандарды азайтудың мағынасындай. Осыдан индуктивті жолмен теріс санды қосу арқылы азайту ережесі шығады.

Көбейту және бөлу амалдары бұрынғыдай орындалады, тек таңбасына мән беру керек. Көбейткіштің біреуінің таңбасы өзгергенде көбейтіндінің де таңбасы өзгереді, ал модулі сол қалпында қалады.

«Рационал сандар» тақырыбында бөлшектер, олардың қасиеттері, бөлшектерғе амалдар, пропорция ұғымы, бөлінгіштік теориясының элементтері және алгебра мен геометрияның кейбір сұрақтары қарастырылады.

«Бөлшектер» тақырыбын оқыту әдістемесіне толығырақ тоқталайық.

Бұл тақырыпты көрнекі-белсенділікпен деңгейлеп оқытамыз. Циркульдің инесін қандай да бір О нүктесіне шаншып тұрып, қарындашы бар сирағымен осы О нүктесін айналдыра сызық сызамыз. Сонда қарындаш О нүктесінен бірдей қашықтықтағы нүктеден құралған шеңбер деп аталатын тұйық сызық сызады (1-сурет) . О нүктесі шеңбердің центрі деп аталады.

1-сурет.

Әртүрлі шамаларды (ұзындықты, массаны, уақытты) өлшеу үшін натурал сандардан басқа бөлшек сандар деп аталатын жаңа сабақ енгізілген. 2-суретте дөңгелек (тұтас бір дене) тең төрт бөлікке бөленген. Мұндай тең бөліктер үлестер деп аталады. 2-суреттегі әрбір үлес-дөңгелекті өзара тең 4 бөлікке бөлгендегі 1 бөлігі, жазылуы дөңгелектің -і; оқылуы: “төрттен бір”.

Демек, 1: 4 деген ; 1:4= , мұндағы сызықша - бөлшек сызығы.

¼ ¼

¼

½ ¾

2-сурет.

Алдымен бөлшек сызығының астындағы сан шығыс септігінде оқылады, сонан соң бөлшек сызығының үстіндегі сан атау септігінде оқылады. Егер осындай үлестің ( -дің) екеуін алсақ, онда ол түрінде жазылады. Оқылуы “төрттен екі”. Егер осындай үлестің үшеуін алсақ, онда ол түрінде жазылады. Оқылуы “төрттен үш”. Мұндағы, ; ; - жай бөлшектер. Жай бөлшектердің жалпы түрде әріппен жазылуы: . Мұндағы: а-жай бөлшектің алымы, в- жай бөлшектің бөлімі.

Бөлшек сызығының астындағы сан неше үлеске бөлінгенін көрсетеді, сондықтан оны бөлшектің бөлімі деп атайды. Бөлшек сызығының үстіндегі сан неше үлестің алынғанын көрсетеді, оны бөлшектің алымы деп атайды. Кез келген натурал сан жай бөлшектің бөлімі, ал 0 саны және кез келген натурал сан алымы бола алады.

Есеп. Егер екі алманы үш балаға тең бөліп берсек, олардың әрқайсысы неше бөліктен алма алады.

Шешуі: Алманың әрқайсысын үш тең бөлікке бөлеміз. Әрбір бөлік алманың 1/3 -і болады. Бір балаға осындай 2 бөліктен беріледі. Балалардың әрқайсысы алманың 2/3

бөлігін алады. Жауабы: 2/3 бөліктен.

Алымы 1 саны, бөлімі кез келген натурал сан болатын бөлшектерді бірлік бөлшектер дейміз. Мысалы: ; ; .

Жай бөлшектің негізгі қасиеті. Жай бөлшекті қысқарту.

Дөңгелекті өзара тең төрт бөлікке бөліп, оның үш бөлігін бояйық (3-сурет) . Сонда дөңгелектің -і боялады.

3-сурет.

Әрбір бөлікті тағы да өзара тең 2 бөлікке бөлсек, онда дөңгелектің -сы боялады.

Демек, = ; = .

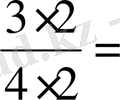
Осыдан шығатын қорытынды:

Жай бөлшектің алымын да, бөлімін де бірдей натурал санға көбейткеннен немесе бөлгеннен жай бөлшек өзгермейді.

Бұл бөлшектің негізгі қасиеті.

= = .

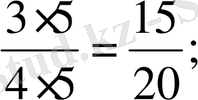
Бөлшектің алымын да, бөлімін де олардың 1 ден өзге бөлгішіне бөлуді бөлшекті қысқарту деп атайды. Бөлшекті қысқарту тәсілдеріне тоқталсам. 1тәсіл. Бөлшектің алымын да, бөлімін де олардың ең үлкен ортақ бөлгішіне бөлу арқылы қысқарту.

Мысалы: ЕҮОБ (42, 63) =21, онда =

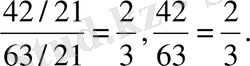
2 тәсіл. Бөлшектің алымы мен бөлімін көбейткіштерге жіктеп, ортақ бөлгішті таңдап ала отырып қысқарту. Мысалы: =

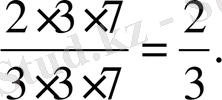
Бөлшектер алымы мен бөлімі өзара жай сандар болғанша қысқартылады. Алымы мен бөлімі өзара жай сандар болатын бөлшектер қысқартылмайтын бөлшектер деп аталады.

Мысалы: ;

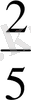
Дұрыс бөлшектер және бұрыс бөлшектер, аралас сан.

Жай бөлшектің алымы бөлімінен кіші болуы мүмкін, оған тең болуы немесе бөлімінен үлкен болуы мүмкін.

Егер бөлшектің алымы бөлімінен кіші болса, онда ол бөлшек дұрыс бөлшек деп аталады.

Мысалы: , дұрыс бөлшектер. 2<3, 4<9 сондықтан дұрыс бөлшек 1-ден кіші.

Егер бөлшектің алымы бөліміне тең немесе одан үлкен болса, онда бөлшек бұрыс бөлшек деп аталады.

Мысалы: 5=5, 10>9, 6=6.

Бүтін бөліктен және бөлшек бөліктен тұратын сан аралас сан деп аталады. Мысалы: 2+ .

Бұрыс бөлшекті аралас санмен жазу төмендегі деңгейлерден тұрады:

1. Бөлшектің алымын бөліміне бөлу керек. =7:5=1 (қалд. 2)

2. Толымсыз бөлінді аралас санның бүтін бөлігі болады.

3. Қалдық ( егер ол бар болса) бөлшек бөліктің алымы, ал бөлгіш бөлімі болады.

Аралас санды бұрыс бөлшек түрінде жазу үшін:

1. Аралас санның бүтін бөлігінің бөліміне көбейту керек.

2. Шыққан көбейтіндіге бөлшек бөлігінің алымын қосып, алым ету керек.

3. Бөлшектің бөлімін өзгертпей, бөлім етіп қалдыру керек.

Ал енді жай бөлшектерге қолданылатын амалдарға келсем, жай бөлшектерді қосуға, алуға, көбейту және бөлуге болады.

Жай бөлшектерді қосу . Бөлімдері бірдей бөлшектерді қосуды қарастырайық Мысалы: қосындысын табайық.

4-сурет.

4-суреттен екенін көруге болады.

Бөлімдері бірдей бөлшектерді қосқанда олардың алымдарын қосып, алым етіп, ал сол бөлімнің өзін қалдыру керек. Бөлімдері бірдей бөлшектерді қосу ережесі әріп түрінде: .

Бөлімдері әртүрлі бөлшектерді қосу үшін: