Радикал арқылы шешілетін теңдеулер

Кіріспе
1.Өрістердің автоморфизмдері
2.Галуа группасы, оның реті
3.Галуа сәйкестігі.
4.Қарапайым радикалды өсімшелер.
5.Циклды өсімшелер
6.Радикалды өсімшелер.
8. Галуа группасы шешілетін группа болатын нормальды өрістер.
9.Радикал арқылы шешілетін теңдеулердің негізгі теоремасы.
9.Симметриялы, таңбасы өзгермелі группалар S2 S3 S4 . группаның шешілетін группа болатындығы.
10.S5 (А5) . группасының шешілмейтіндігі.
Әдебиеттер тізімі

1. М.М.Постников «Теория Галуа» М. 1963г.
2. Б.Л. ван дер Варден «Алгебра» М. «Наука», 1979г.
3. Богомолов А.Н. «Математики, механики» Киев «Наукова думка», 1983г.
4. М.М. Постников «Группы и алгебра Ли» М. «Наука», 1982г.
5. А.И. Кострикин «Введение в алгебру» М: «Наука», 1977г.
6. В.А.Любецкий основные понятия школьной математики М. «Просвещение» 1987г.

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 32 бет
Таңдаулыға:

Тақырыптың өзектілігі. Алгебралық системалардың кейбір түрлері
математикада жиі кездеседігі сонша, тіпті оларды зерттеу өз алдына жеке
теориялардың пәні болып кеткен. Осындай алгебралық системалардың ең
қарапайымы группалар болып табылады.
Бұл тарауда Р өрісі белгіленген мүшелік ретінде ұйғарылады. Біз
бұл өрісті негізгі өріс деп атаймыз. Қалған барлық өріс бұл негізгі өріс
мағынасының кеңеюі деп ұйғарылады. f(x)-P өрісіндегі жіктелмейтін
көпмүшелік. Р өрісіндегі Р (α1...,αn) мағынасының кеңейтілуі f(x)
көпмүшелігінің α1...,αn барлық түбірлерінен туындайды, осы өріс көпмүшеліктің
жіктелу өрісі деп аталады. Р(α1...,αn) өрістің кез келген элементі α1...,αn
элементінен тұратын көпмүшелік түрде Р өрісінің коффициенттерімен
беріледі.
Егер Р – да жіктелмейтін көпмүшеліктің К-да ең болмағанда бір
түбірі бар болса, онда К-да көпмүшелік сызықтық көбейткішке жіктеледі. Р
өрісіндегі К мағынаның кеңейтілуі, мағынаның бірқалыпты кеңеюуі деп
аталады. Басқаша айтқанда, егер келесі екі шарт орындалса Р өрісінің К
өрісі нормальді кеңейтілуі деп аталады:
1. Р-да К арқылы
2. Егер Р-да жіктелмейтін көпмүшелік К-да ең болмағанда бір түбірді
қамтыса, онда К-да бұл көпмүшелік толық жіктеледі.
Р өрісін орнында қалдыратын автоморфизмдердің жиынтығы К өрісінің
аытоморфизмдер группасының ішкі группасы деп аталады. Егер К өрісі Р
өрісінің нормальды өсімшесі болса, онда бұл ішкі группа Р өрісіне сәйкес К
өрісінің Галуа группасы деп аталады және G(K,Р) арқылы бегіленеді.
Тақырыптың мақсаты: Радикал арқылы шешілетін теңдеулер.
Тақырыптың міндеті:
• Қарапайым радикалды өсімшелер. Циклды өсімшелер. Радикалды өсімшелерді
анықтау.
• Галуа группасы шешілетін группа болатын нормальды өрістерді дәлелдеу.
Радикал арқылы шешілетін теңсіздіктердің негізгі теоремасы.
• Симметриялы, таңбасы өзгермелі группалар. S2 S3S4- группаларының
шешілетін группа болатындығы.
Зерттелу деңгейі. Теңдеулердің Галуа группасын есептеу тақырыбына арналған
зерттеу жұмысын бірінші болып жазған Эварист Галуа. Галуаның негізгі
зерттеулері алгебраға арналады. П. Руффини (1799) және Н. Абель (1824) 4
дәрежелі алгебралық теңдеулердің шешілетіндігі дәлелдеген. Галуа берілген
теңдеуді қанағаттандыратын шарттарды анықтады. Олардың теорияны анықтауы
тек алгебраның дамуына ғана емес, сонымен бірге ХІХ ғасырдағы математика
ілімдегі үлкен жаңалық болды. Группа теориясындағы әдіс және идеялар
жаратылыстану, кванттық механика, крисаллографияда қолданыс тапқан.
Постников Г.Г. Теория Галуа, неміс ғалымы Б.Л.ван дер Варден
Алгебра С.А. Бадаев, Е.И. Бидайбеков Группалар, өріс және сақиналардың
қарапайым қасиеттері атты кітаптар осы тақырыпқа арналған.
Зерттеу жұмыысының көлемі. Кіріспе, 6 - тақырыптан, қортынды, әдебиеттер
тізімі, жалпы беттен тұрады.

Өрістердің автоморфизмдері.

Кез келген К өрісінің өзара бірмәнді S бейнелеуін автоморфизм
деп атайды, егер ол қосындыны қосындыға, ал көбейтіндіні көбейтіндіге
ауыстырса, яғни егер К өрісінің кез келген (, (элементтері үшін

((+()s=(s+(s,
((()S=(S(S (1)

(S автоморфизмі ( элементін (S элементтіне көшіреді)
Автоморфизм бірмәнді өзара сәйкестік болу керек, яғни, (1) шарттан
басқа ол клесі қажеттілікті міндетті түрде қанағаттандырады;
а) кез келген (К элементі үшін (S элементі бірмәнді анықталған
және К-ға тиісті;
ә) егер ((( болса, онда (s((s болады;
б) кез келген ( єК элементі үшін (єК элементі табылады, (S ((
болғанда.
ә) шартынан б) шартымен қаралған ( элементінің бірмәнді екені
анықтамадан шығады.
Демек, бұл элементті (S арқылы:
(( (S,

біз кейбір S-1 қайта құруын аламыз. Бұл құрудың бірмәнді сәйкестігі, кез
келген (єК элементі үшін сипатталады.
((S )S(( (2)

Сонымен S-1қайта құруы автоморфизм болып табылады. Шынында да, кез келген
(єК және (єК элементтері үшін

((S +(S ) S( ((S )S+((S )S((+(

және, олай болса, анықтама бойынша төмендегідей болады

((+()S ((S +(S
((()S ((S (S
теңдігі де ұқсас дәлелденді.
SТ көбейтіндісімен мына S және Т екі автоморфизмдерді қайта
құру деп атайды, нәтижеде S бірқалыпты қайта құруының орындалуы, ал кейін Т
қайта құруы; кез келген (К элементі үшін (SТ элементі мына формуламен
анықталады:

(SТ(((S)Т .

SТ қата құруы да автоморфизм болып табылатыны тұра тексеріледі.
Тапсырма. Автолорфизмдердің көбійтіндісі ассоциативті екенін
дәлелдеу керек. Автоморфизмдерді көбейту, бірлікке ие болу – ол Е мағыналас
автоморфизм ретінде негіз болады, К өрісінің барлық элементтері орнында
болады.

(Е((

Анықтама бойынша ((2) формулаға қарау)

S-1S(Е (3)

Енді (S-1)-1автоморфизмін қарастырайық, S-1автоморфизмге кері. Анықтама
бойынша

(S-1)-1∙S-1(Е (4)

Осы теңдіктің оң жағына S-ті көбейтіп және (3) формуланы қолданып, келесіні
аламыз

(S-1)-1(S

Мұны (4) формулаға қойып, төмендегіні аламыз

SS-1(Е.
Сонымен,
S-1S(SS-1(Е.

Мұнда, біз операцияға қатысты автоморфизмдердің көбейтіндісі
арқылы автоморфизмдердің жиыны группа болатындығын көреміз. Бұл группа К
өрісінің автоморфизмдер группасы деп аталады.
Тапсырма. Кез келген автоморфизмдер барлық рационал сандарды
орнында қалдыратынын дәлелдеу керек (дербес жағдайда, 0 және 1 сандарын).
Айталық Р- кейбір К өрісінің ішкі өрісі болсын. К өрісінің
Sавтоморфизмі Р өрісіндегі автоморфизм деп аталады, егер ол Р өрісінің
барлық элементтерін орнына қалдырса, яғни егер кез келген сєР элементі үшін

сS(с

Р өрісіндегі барлық автоморфизмдердің жиынтығы К өрісінің автоморфизмдер
группасының ішкі группасы болып табылады. Егер К өрісі Р өрісінің нормальды
өсімшесі болса, онда бұл ішкі группа Р өрісіндегі К өрісінің Галуа
группасы деп аталады және G(К,Р) таңбасымен белгіленеді.
Айталық
f(х)( с0+с1х+...+сnхn; f(()(0

- (-ның ең болмағанда бір түбірі К-да болатын, Р өрісіндегі кез келген
көпмүшесі
болсын;
с0+с1(+...+сn((0 (5)

G(К,Р) Галуа группасынан S автоморфизмін (5) тепе теңдікке қолданып,
келесіні аламыз;
с0+с1(S+...+сn((S)n(0

(әйтпесе сі S(сіS кез келген i(0,1...,n үшін), яғни

f((S)(0
Сонымен,
G(К,Р) Галуа группасынан барлық автоморфизмдер Р өрісіндегі кез
келген көпмүшенің әр бір түбірін қайтадан осы көпмүшенің түбіріне көшіреді
(ауыстырады).
Дербес жағдайда, бұдан
кез келген (К саны және кез келген SG (К,Р) автоморфизм
үшін К өрісіндегі ( санымен (S саны түйіндес.
Ескерту. Егер сызықтық түрлендіруді белгілі түсінік ретінде қабылдасақ,
онда нөлден өзгеше вектор нөлдік векторға ауыспайтын ақырлы кеңістіктің
сызықтық түрлендіруі сонда және сонда ғана өзара бірмәнді, сондай – ақ
кездейсоқ ақырлы өсімше үшін анықтамадағы автоморфизмнің түсінігін шарт
бойынша Р өрісіндегі К өрісінің өзара бір мәнді деп көрсетуге болады, яғни
1) қасиетке ие болатын және Р өрісінің барлық элементтерін орнында
қардыратын ақырлы К өсімшенің кез келген S бейнелеуі өзара бірмәнді, яғни
Р өрісіндегі К өрісінің автоморфизмі болып табылады.
Шынында да, егер сєР және (єК, онда

(с()S(сS(S(с(S

Бұдан басқа, К өрісінің кез келген ( және ( элементтері үшін

((+()S((S+(S

Бұл, Р өрісіндегі қарастырылатын S бейнелеуі К өрісінің сызықтық (ақырлы)
түрлендіруі болып есептелінетінін белгіленеді. Сондықтан, сызықтық
түрлендіру теориясынан жоғарыдағы деректе берілгенді дәлелдеу үшін, формула
бойынша бекітудің жеткіліктігін көрсетеді, сондай –ақ егер ((0, онда αS(0.
Бірақ егер ((0, онда К өрісінде мынадай ( элементі табылады, сондай – ақ
(((1 және, олай болса, (S(S(1
Сонымен, (S(0 шындық.

Галуа группасы, оның реті

Айталық К өрісі - Р өрісінің кез келген нормальды өсімшесі
болсын. К өсімшесі қарапайым алгебралық өсімше болып табылады, яғни К-да
мынадай θ элеметі табылады
К (Р (θ)

θ элементінің f(х) минималды көпмүшелік дәрежесі n Р өрісіндегі К өрісінің
[К:Р] дәрежесіне тең. К өрісінің кез келген ( элементі бірмәнді жазу
түріне ие болады.

((с0+с1 θ +...сn-1 θ n-1, с0с1,...сn-1Р (1)

Алдынғы пунктте дәлелденген бойынша,G(К,Р) Галуа группасының
кез келген S автоморфизімі θ түбірін қайтадан f(х) көпмүшесінің түбіріне
ауыстырылады. Басқа сөзбен айтқанда, әрбір S G(К,Р) автоморфизмге f(х)
көпмүшенің кейбір түбірі сәйкес келеді. Осы сәйкестікті толық зерттейміз.
Айталық θ ' - f(х) көпмүшенің кез келген түбірі болсын. К өрісі
нормальды және болғандықтан, онда θ 'К. К өрісіндегі S қайта
құруын, осы өрістің кез келген (1) элементті орнына қою арқылы анықтаймыз.

(S(с0+с1 θ +...+сn-1 θ n-1 (2)

( элементінің жазылуы (1) түрде бірмәнді, онда (2) формуланың (S элементі
бір ғана амалмен анықталады.
S түрлендірудің анықтамасын келесі түрде формула арқылы анықтауға
болады; егер

((g (θ)

g(х) – n нен кіші дәрежесі бар Р өрісіндегі көпмүше болса, онда

(S(g(θ ')

Енді Р өрісіндегі кез келген дәрежелі g(х) көпмүшесін қарастырайық, және
айталық

((g(θ)

болсын. g(х) көпмүшесін f(Х) көпмүшесіне (қалдықпен) бөлеміз:

g(х)(f (х)q (х) + r(х). (3)

бұл теңдіктен х( θ деп ұйғарып, f(θ) (0 болғандықтан, біз мына теңдікті
аламыз

((r(θ)

r(х) көпмүшенің дәрежесі n –нен кіші болғандықтан, онда бұдан шығады:

(S(r(θ ')

Басқаша жағдайда, (3) формуладан х(θ' деп ұйғарып, келесісін аламыз.

g(θ)(r(θ')
Демек,
(Sg(θ ')

Сонымен,
g(θ)S(g(θ ')

g(х) көпмүшесінің дәрежесіне байланыссыз.
Айталық

(1(g1(θ), (2(g2(θ)

- К өрісінің кез келген элементі болсын. Сонда
-
(1+(2(g1(θ)+g2(θ),
(1(2(g1(θ)g2(θ)

және, олай болса,

((1+(2)S(g1(θ ')+g2(θ ')((1S+(2S;
((1(2)S(g1(θ ')g2(θ ')((1S(2S

Сонымен, S түрлендіруі қосынды мен көбейтіндіні сақтайды, яғни (1) шартына
ие болады. Бұл түрлендіру Р өрісінің барлық элементтерін орнына қалдырады.
Сондықтан S түрлендіруі Р өрісіндегі К өрісінің автоморфизмі болып
табылады, яғни G (К,Р) Галуа группасына жатады.
S түрлендіруі автоморфизм болып табылады, яғни (1) шарттан тыс өзара
бірмәнді қасиетін дәлелдеу мүмкіндігі шындық. Шынында да, Р(θ ') өрісін
қарастырайық. θ 'К болғандықтан, онда
Р(θ ') К.

Басқаша жағдайда, Р өрісіндегі Р(θ ') өрісінің дәрежесі f(х) көпмүшесінің
дәрежесіне тең, яғни К өрісінің дәрежесіне тең. Демек,

Р(θ ')(К

Бұдан, (1) жазуымен қатар К өрісінің кез келген ( элементі мағыналас түрде
жазылатыны шығады
((с0+с1 θ +...+сn-1 θ 'n-1, (4)

мұндағы
с0,с1, ... сn-1Р

Енді К өрісінің S' түрлендіруі өзгерту функциясын, осы өрісте
әрқандай элементке (4) қою арқылы анықтаймыз.
(S (с0'+с'1 θ +...сn-1' θ n-1
S'S(SS'(Е

болғандықтан, (яғни S'(S-1), онда S түрлендіруі К өрісіндегі мәндес
түрлендіруі болып табылады яғни автоморфизм болып табылады.
S автоморфизмнен құралған θ түбірі θ ' түбіріне ауысады:

θ S( θ ',

яғни жоғарғы мағынада көрсетілген бұл автоморфизм θ' түбіріне сәйкес
келеді. Сонымен, кез келген f(х) көпмүшесінің түбірі үшін G (К,Р) Галуа
группасында осы түбірге сәйкес келетін автоморфизмнің табылатыны
дәлелденді. Түбірмен сәйкес келетін автоморфизм бірмәнді анықталады, яғни
егер,

θS( θ Т
онда
S(T

Шынында да, егер θ S( θ Т болмаса, онда θ ST-1( θ болады, яғни ST-1
автоморфизм θ түбірін орнына қалдырады және, олай болса, төмендегі кез
келген түрді орныда қалдырады
с0+1 θ + ... +сn-1 θ n-1, мұндағы с0,с1,...сn-1,

яғни К өрісінің кез келген элементін орнында қалдырады. Сөйтіп, ST-1(Е және
S(T
Сонымен, G (К,Р) Галуа группасының элеменнтері (яғни Р өрісіндегі К
өрісінің автоморфизмдері) f(х) көпмүшенің түбірлерімен сәйкес келетін өзара
бірмәнді, және олай болса, олардың сандары, яғни G (К,Р) группаның реті
f(х) көпмүшенің түбірінің санына тең, яғни n- ге тең (бұл көпмүше
келтірілмеген болғандықтан, барлық f(х) көпмүшенің түбірлері әр түрлі).
Сонымен біз,
G (К,Р) Галуа группасының реті Р өрісіндегі К өрісінің дәрежесіне тең
екенін дәлелдедік.

Галуа сәйкестігі.

Айталық, К(Р(θ)- кез келген негізгі Р өрісінің нормальды өсімшесі және
G (К,Р) – оның Р өрісіндегі Галуа группасы болсын.
Бұл пункте біз К өрісіндегі Р өрісінің L ішкі өсімшесін қарастырамыз:

Р LК

Мұндай өсімшелерді біз аралық өрістер деп атаймыз.
θ саны түбірі болып табылатын, Р өрісіндегі f(х) көпмүшесін, және әр қандай
L аралық өрісінің көпмүшесін қарастырып алуға болады. Сірә, оның L-дегі
жіктеу өрісі L(θ) өрісі болып табылады. Демек, L өрісіндегі L(θ) өрісі
нормальды. Басқаша жағдайда, РL болса, онда 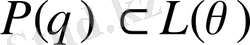, яғни 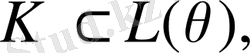ал
және болса, онда L(θ)К болады. Демек, К(L(θ)
Сөйтіп,
К өрісі әр қандай аралық L өрісінде нормальды.
Сондықтан L өрісіндегі К өрісінің G (К,L) Галуа группасы туралы
сөйлеуге болады. Алдынғы пункте дәлелденгенмен келісіп, G (К,L) группаның
реті L өрісіндегі К өрісінің дәрежесіне тең.
Анықтама бойынша, G (К,L) группаның элементтері, әр қандай L өрісінің
элементерін орнында қалдыратын К өрісінің автоморфизмдері болып табылады.
РL болса, онда автоморфизмдер кез келген Р өрісінің элементтерін
орнында қалдырады, яғни Р өрісіндегі К өрісінің G (К,Р) Галуа группасының
элементтері болып табылады. Сөйтіп,
G (К,L) G (К,Р)

яғни L өрісіндегі К өрісінің Галуа группасы Р өрісіндегі К өрісінің Галуа
групасының ішкі группасы болады. Оның реті L өрісіндегі К өрісінің [К;L]
дәрежесіне тең.
Айталық Н- G (К,Р) Галуа группасының кез келген ішкі группасы болсын. Н
ішкі группадан әр қандай автоморфизмдер орнында қалдыратын, К өрісінің
барлық элементтерінің жиынтығы К өрісінің ішкі өрісі болып табылады. Бұл
ішкі өріс Р өрісін құрайды, яғни аралық өріс болып табылады. Біз оны
К(G,Н) арқылы белгілейміз.
Айталық
Т1(Е, Т2,... Тm

- Н ішкі граппасының барлық элементтері болсын. (сөйтіп, m-Н ішкі
группасының реті). Төмендегі көмүшені қарсырайық.
h(х)((х- θ ті)
(1)
Сандары оның түбірлері болып табылады.
әр қандай ТєН автоморфизмінде бұл сандар

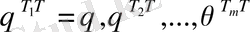(2)
Сандарына өтеді. Бірақ
Т1Т(Т, Т2 Т,.. Тm Т
элементері, Н ішкі группасының барлық элементерін тауысады. Демек, ретке
дейін шығатын дәлдікпен (2) сандары (1) сандарымен тура келеді. Басқа
сөзбен айтқанда, әр қандай ТєН автоморфизмінде h(х) көпмүшесінің түбірі тек
орын – орнына қойылады. Сондықтан, осы түбірлерден кез келген симмериялы
көпмүше, дербес жағдайда h(х) көпмүшенің кез келген коэффициенті, Т
автоморфизмде орнында қалады және, олай болса (Т-Н ішкі группадағы кез
келген автоморфизмін де), К (G,Н) өрісіне жатады. Сөйтіп, h(х) көпмүшесі
К (G,Н) өрісіндегі көпмүше болып табылады.
Демек, К (G,Н) өрісіндегі Ө элементінің минималды көпмүшесі h(х)
көпмүшесінің бөліндісі болып табылады, және сондықтан оның дәрежесі (яғни К
(G,Н) өрісіндегі θ санының дәрежесі) m-ге тең немесе аз. Бірақ θ санынан
шыққан К өрісі кез келген аралық өрісінің қарапайым алгебралық өсімшесі
болып табылатынын жоғарыда көрдік. Сондықтан К (G,Н) өрісіндегі К
өрісінің дәрежесі θ санының минималды көпмүшенің дәрежесіне (К (G,Н)
–қа)тең, яғниң дәлелдеме бойынша, m-ге тең немесе аз.
Енді L( К(G,Н) өрісіндегі К өрісінің G(К,L) Галуа группасын
қарастырайық. Бұл группаның реті К (G,Н) өрісіндегі К өрісінің
дәрежесіне тең және сондықтан m-ге тең немесе аз. Басқаша жағдайда,
анықтама бойынша, G(К,L) группасы L(К(G,Н) өрісінің элметерін орнында
қалдыратын К өрісінің барлық автоморфизмдерінен тұрады және сондықтан Н
группасын құрайды. Демек, оның реті m-нен аз болуы мүмкін емес.
Бұдан G(К,L) группасының реті m-ге тең және сонда ол Н ішкі группамен тура
келетіні шығады. Сөйтіп,

Егер L(К(G,Н), онда G(К,L) (Н

Айталық L- кез келген аралық өріс болсын, және Н(G(К,L) болсын К (G,Н)
өрісін қарастырайық.
LК(G,Н)
[К(G,Н):L](

Басқаша жағдайда, жаңа ғана дәлелдеме бойынша, К (G,Н) өрісіндегі К
өрісінің [К:К(G,Н)] дәрежесіне Н(G(К,L) группасының ретіне тең, яғни L
өрісіндегі К өрісің [К:L] дәрежесіне тең. Демек, [К(G,Н):L](1, яғни
L(К(G,Н).
Сонымен
егер Н(G(К,L) болса онда, К(G,Н)(L болатыны дәлелденді
Сөйтіп, біз әр қандай аралықтағы L өрісіне G(К,Р) группасының кейбір ішкі
группасына сәйкес келетінін,G(К,Р) группасының кез келген Н ішкі группасы
үшін L аралық өрісі табылатынын, және бұл ішкі группаның сәйкес келетінін,
және әртүрлі аралықтағы өріске әртүрлі ішкі группаның сәйкес келетінін
көріп тұрамыз, егер G(К,L1)( Н(G(К,L2) болса, онда келесіні аламыз

L1(К(G, G(К,L1))(К(G,G(К,L2))(L2

Басқа сөзбен айтқанда, біз аралық өрісінің барлығын және Галуа группасының
ішкі группасының барлығын бірмәнді сәйкестік арасында құрдық. Бұл
сәйкестік Галуа сәйкестігі деп атайды.
Тағы бір рет,
Галуа сәйкестігінде нормальды К өрісінің L аралықтағы ішкі өрісіне L
өрісіндегі К өрісінің G(К,L) Галуа группасы сәйкес келетінін, ал Н ішкі
группада G(К,L) группасы - К(G,Н) ішкі өрісіне, К өрісінің барлық
элементтерінен тұртынын, Н- тан әрбір автоморфизмдердің орнына қалғанын
қайталайық. G(К,L) группаның реті L өрісіндегі К өрісігің дәрежесіне тең,
К(G,Н) өрісіндегі К өрісінің дәрежесі Н группасының ретіне тең.
Дербес жағдайда, барлық G(К,Р) группаға Р өрісі сәкес келеді. Демек,
G(К,Р) группасынан әрбір автоморфизмде орнында қалдыратын Р өрісі К
өрісінің барлық элементтерінен тұрады.
Бірлік Е ішкі группаға, яғни тек қана тепе – теңдік Е автоморфизмнен
тұратын ішкі группаға барлық К өрісі сәйкес келеді.
Галуа сәйкестігі берілген ішкі өрістің теориясына нормальды өрістің кейбір
бейнелеу мағынасына Галуа группасы оның ішкі группасының теориясын және
осы ішкі өрісті зерттеуге теоритика – группалық методты қолданады. Мысалы,
арқылы группаның ішкі группасының ақыры сандарынан кез келген нормальды
өрістің ішкі өрісінің аралық саны ақырлы екені шығады. Бұл фактті Галуа
сәйкестігін қолданбай дәленденген қиын. Галуа сәйкестігін қолданғанда, ол
әрқашан кірістіру таңбасына айналу түрде болуы керек, яғни егер К
өрісінің L1 және L2 ішкі өрістерімен оның Галуа группасының Н1 және Н2 ішкі
группалары сәйкес келсе, онда

L1 L2 (3)
(3)–тен,
Н1 Н2 (4)

Шығады, және керісінше, (4)- тен (3) шығады.

Қарапайым радикалды өсімшелер.

Р өрісінің қарапайым радикалды өсімшесі дегеніміз, екімүшелі
теңдеу түріндегі К-ның жіктеу өрісін айтады, яғни төмендегідей.

хn -((0, мұндағы ( Р, (≠0 (1)

1) теңдеудегі барлық түбірлерді жеке nдәрежелі түбірге бірден көбейту
мен алынытыны белгілі. Бірақ кез келген n дәрежелі түбір бір амалды
түбірдің дәрежесі болып табылады. Сөйтіп, егер θ - (1)теңдеудің кез келген
түбірі болса, ал кейбір жеке n дәреженің бір амалды түбірі болса,
онда

θ ( θ ζ0, θ ζ, ... θ ζn-1 (2)
сандары (1) теңдеудегі барлық түбірлерді тауысады.
Демек, Р(ζ, θ) өрісі (1) теңдеудің барлық түбірлерді құрайды, және сол
себептен

КР(ζ, θ)

Басқаша жағдайда К өрісі θ және θ ζ сандарын құрайды және сол себптен θ
және ζ( θ ζ θ сандарын құрайды. Демек,
Р(ζ θ)К
Сөйтіп,
К(Р(ζ ,θ)

Сондай –ақ Р өрісі ζ түбірін құрайтыны мүмкін. Мұндай жағдайда К қарапайым
радикалды өсімшеде Р(θ) түбірі болады. Қашан α(1 болады, сонда басқа санға
кездейсоқ пайда болады. Мұндай жағдайда біз θ түбірі ретінде 1 санын
алуымызға болады, сондай – ақ К (Р(ζ)
К (Р(ζ θ) өрісінің жіктеу өрісі болып табылатыны нормальды және сондықтан
оның G(К,Р) Галуа группасы туралы сөз айтуымызға болады.
Айталық S-G(К,Р) Галуа группасындығы кез келген автоморфизмі
болсын. саны хn-1 көп мүшенің түбірі болғандықтан, онда ζS саны да
осы көпмүшенің түбірі болады. Демек, мынадай саны табылады, сондай –
ақ

ζS(ζа (3)

егер ζа саны хm-1 көпмүшесінің түбірі болса, мұндағы mn болсын, онда және
ζ((ζа)S саны да хm-1 көпмүшесінің түбірі болады, яғни бірліктегі mn
дәрежесінің түбірі болатые еді. Бірақ бұл мүмкін емес, себебі шарт бойынша
ζ саны бірліктегі n дәрежесінің бір амалды түбірі болып табылады. Демек,
ζа саны бірліктегі m дәреженің түбірі болуы мүмкін емес, mn, яғни n
діреженің бір амалды түбірі болады. Сондықтан а саны n санымен өзара жай.
Осыдан кейін, 0 саны (1) теңдеуінің түбірі болғандықтан, онда және θ S
саны да (1) теңдеудің түбірі болады, яғни мынандай b саны табылады, сондай
– ақ

θ S (ζb θ (4)

Сөйтіп, әрбір G(К,Р) автоморфизмге а және b қос сандары сәйкес келеді,
және де а саны n санымен өзара жай. Бұл сәйкестік бірмәнді емес, әйпесе,
мысалы (а1b1) қос, а1 және b1 сандарының а және b1 сандарынан айырмашылығы
бар n еселі санына, сонымен қатар S автоморфизміне де сәйкес келеді. Бұл
сұрақты қарастырайық.
Айталық (а,b) және (а1b1)жұптар бір жіне сол S автоморфизмге сәйке келсін,
яғни

ζS(ζа, ζS(ζа,
θ S(ζb θ, θ S(ζb θ
болсын. Сонда
ζа(ζа, ζb(ζb
яғни
ζа-а(1, ζb-b(1

ζ- біртекті n дәреженің бір амалды түбірі болғандықтан, онда а-а1 және b-
b1 айырмашылықтары n-ге бөлінсе, яғни n модулі бойынша салыстырмалы а және
b сандары а1 және b1 сандарымен сәйкес келсе онда және санда ғана бұл
теңдіктер мүмкін. Басқа сөзбен айтқанда, (а,b ) және (а1 b1) жұптары бір
класқа жатса, яғни Мn группаның бір және [а,b] элементін анықтаса, сонда
және санда ғана бұл жұптар бір және SG(К,Р) автоморфизмге сәйкес
келеді.
Сөйтіп, егер біз (3) және (4) формулаларда а және b сандары анықталатын
G(К,Р) Галуа группадағы әрбір S автоморфизмге Mn группаның [a,b] элементін
жатқызсақ, онда Мnгруппадағы G(К,Р) группаның бірмәнді бейнелеуін
аламыз. Бұл бейнелеуді біз әрпімен белгілейміз:

φ(S)([а,b]

Сондай –ақ φ бейнелеуі гомоморфты болады. Шынында да, егер φ(S)([а,b] және
φ(Т)([с,d] болса, яғни егер
ζS(ζа, θ S(ζb θ
ζт(ζс, θ т(ζd θ
онда
ζSт((ζа)т((ζт)а(ζас
θ Sт((ζb θ)т((ζт)b θ т(ζbсζd θ (ζbс+d θ

Сөйтіп,
φ(SТ)([ас, bс+d]
яғни
φ(SТ)(φ(S) φ(Т)

φгомоморфизмнің ядросын табайық. Егер SєG(К,Р) автоморфизмі φ
голоморфизмнің ядросына жатса онда
ζS(ζ, θ S( θ,

яғни S автоморфизмі ζжәне Ө элементерін орнында қалдырады. Демек, S
автоморфизмі ζ және Ө элементерден кез келген көпмүшені орнында қалдырады.
Сондықтан, К(Р(ζ,Ө) өрісінің кез келген элементі ζ және θ - дан көпмүше
түрінде көрсетіледі, сонда S автоморфизмі К өрісінің кез келген элементін
орнында қалдырады, яғни S(Е. Сөйтіп, φ голоморфизмнің ядросы тек қана Е
автоморфизмнің тепе- теңдігінен тұрады, яғни φ мономорфизм болып табылады.
Басқа сөзбен айтқанда, φ Мn группаның кейбір ішкі группасына G(К,Р)
группаның изоморфты бейнелеуін жүзеге асырады. Мn группасы (сол себептен
және оның кез келген ішкі группасы) шешілетін болса, онда бұдан,
қарапайым радикалды өсімшенің Галуа группасы шешілетін группа болып
табылатыны шығады.
Егер ζєР, яғни егер К(Р(θ), онда φ мономорфизмі [1,n] түріндегі
элементтерден тұратын Мn группаның Nn ішкі группасында бар болады. Бұл ішкі
группа Zn группасында изморфты болғандықтан, онда бұдан, егер ζєР, К(Р(θ)
қарапайым радикалды өсімшенің Галуа группасы циклды группа болады, n санына
бөлінетін рет.
Қарама – қарсы тұрған жағдайда, d(1 болғанда, яғни К(Р(ζ) және θ (1
болғанда, Мn группа ішкі группасында [а,0] түріндегі барлық элементтерден
тұратын φ монорфизмін құрайды. Бұл ішкі группа Zn' группасында изоморфты
болғандықтан, онда бұдан,
ζ- бірліктегі n дәреженің бір амалды түбірі болатын, Р өрісінің
К(Р(ζ) қарапайым радикалды өсімшесінің Галуа группасы, Zn' группасының
кейбір ішкі группасы изморофты және сол себептен абелді екені шығады.

Циклды өсімшелер

Р өрісінің нормальды К өсімшесі циклды өсімше деп аталады, егер оның
Галуа группасы циклды группа болса, n дәрежесі екі мүшелі теңдеумен
анықталатын, сондай-ақ шартты негізгі Р өрісі біріліктегі n дәреженің бір
амалды түбірін құрайтын, циклды өсімше мысалында қарапайым радикалды
өсімшеге жатуы мүмкін. Бұл өсімшенің m дәрежесі, жалпы айтқанда, n-нен аз.
Осы қарапайым радикалды өсімшені анықтайтын 1 n –ғы (1) теңдеу
келтірілмегенде, m=n теңдігі сонда және сонда ғана орын алады.
Келесі керісінше бекітудің дәлелдеуі осы пункттың мақсаты болып
табылады.
Егер Р өрісі бірліктегі n дәрежесінің бір амалды түбірін құрайтын
болса, онда n дәрежесі келтірілмеген екі мүшелі теідеумен анықталатын,
оның кез келген К циклды өсімшесінің n дәрежесі қарапайым радикалды өсімше
болып табылады.
Бұл бекітудің дәлелдеуінде біз бір неше алғашқы ескертулерді
қолданамыз.
Айталық - бірліктегі n дәреженің бір амалды түбірі болсын, ал S –
кейбір G (К,Р) групасын көрсететін болсын (бұл группа циклды, яғни оның
элементтері S0(E,S1,...,Sn-1 дәрежелермен жеткілікті). К өрісінің әрқандай
α элеметтеріне төменгі элеметтерді қарастырайық.

яғни мына элементті

мұндағы t- кейбір бүтін сан. () элементін біз t сананы сәйкес келетін,
элеметтінің Ларгранж резальвенті деп атаймыз.
Бірінші біз 1 санына сәйкес келетін резальвентті қарастырайық.

є К болғандықтан, онда Р ()К болады. Демек, Галуа
сәйкестігінде Р () өрісіне G (К,Р) группаның кейбір Н ішкі группасы
жауап береді. (Н(G(К,Р()).
Циклды группаның ішкі группасы болғандықтан, Н группасы циклды. Соған
көрсетілгендей S элементін алуға болады, мұндағы d-H ішкі групаның индексі.
SdєН(G(К,Р()) болса, онда S (α және олай болса, кез келген і және
j үшін сондықтан, Н групаның ретін m=nd белгілеуі арқылы, біз
төмендегіні аламыз, сондай-ақ

Бірақ егер dn болса, онда болады, және сол себептен

әйтпесе . Сонымен, егер dn болса, онда Демек, егер
болса онда d=n болады. Басқаша жағдайда, d=n теңдігі Н=Е, яғни Р
беріледі.
Сонымен.
Егер (ζ,α)≠0 болса, онда Р (α)(К болатыны дәлелденді.
әрине осы бекітумен байланысты мұндай αЄК элементтері табылғаны туралы
сұрақ туады, сондай –ақ (ζ,α)≠0. Осы сұраққа жауап табу үшін біз
теореманы пайдаланамыз. Осы теорема бойынша К өрісінде мынадай θ элементі
шығады, сондай-ақ
К( Р(θ)

[К:Р](n болғандықтан, онда θ n дәреженің келтірілмеген теңдеудің түбірі
болады. Біз сондай-ақ ең болмағанда бір резольвенттегі нөлден өзгешелігін
көрсетеміз.

(ζ, θ), (ζ, θ 2),..., (ζ, θ n-1) (1)

Шынында да, егер барлық (1) резолвенттер нөлге тең болса яғни егер

θ +ζ θ S +...+ ζn-1 θ S ( 0
θ 2+ζ(θ 2)S+...+ ζn-1(θ 2)S (0
... ... ... ... ... ... ... ... ... ... ... .
θ n-1+ζ(θ n-1)S+...+ζn-1(θ n-1)S -(0

онда, сол себептен
(ζ,1)(1+ζ+...+ζn-1(0
төмендегі көрсеткіш нөлге тең (оның бағаналары сызықты тәуелді)

1 1...1
θ θ S... θ S
θ 2 (θ 2)S...( θ 2)S
. . .
. . .
. . .
θ n-1 (θ n-1)S...( θ n-1)S

Басқаша жағдайда, S бейнелеуі автоморфизм болса, онда кез келген і және j
үшін

(θ i)S(( θ S)i

Демек, жоғарыда жазылған көрсеткішті келесі түрде жазуға болады:

1 1...1
θ θS... θS
θ2 (θS)2...( θS )2
. . .
. . .
. . .
θn-1 (θS)n-1...( θ)
(2)

Алынған көрсеткіш θ, θS,..., θS элементтердің Вандермонд көрсеткіші болып
есептелінеді. Ол осы элементтердің айырмашылығына әр түрлі түрлендіруге тең
екені белгілі. Бірақ біз, осы элементтердің арасында бірдейдің жоқтығын
білеміз (егер θS (θS, онда Si (Sj ). Сондықтан (2) көрсеткіш нөлден
өзгеше. ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.