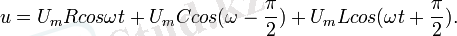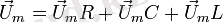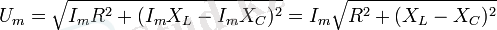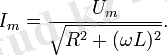Электр тізбектерін талдау: беттесу, генератор және жұлдызша-үшбұрыш түрлендіру; айнымалы ток, Ом заңы және резонанс


Жоспар
- Негізгі түсініктер. Беттесу әдісі . . . 3
- Генератор әдісі . . . 6
- Жұлдызша жазылудан үшбұрыш жалғауына көшу . . . 8
- Айнымалы ток тізбегіндегі актив кедергі. Кернеу мен ток күшінің әсерлік мәні . . . 10
- Айнымалы ток тізбегіндегі сыйымдылық . . . 12
- Ом заңы . . . 13
- Айнымалы ток тізбегіндегі ток заңы . . . 17
- Айнымалы ток тізбегіндегі резонанс . . . 19
- Контурлы ток . . . 19
- Екі түйін әдісі . . . 20
- Көп түйінді потенциал . . . 22
- Есептеу бөлімі . . . 24
- Пайдаланылған әдебиеттер . . . 33
Негізгі түсініктер.
Беттесу әдісі.
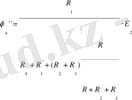
Егер электр сұлбасында екі немесе одан да көп кернеу көзі болса, беттесу әдісі қолданылады. Біз екі кернеу көзі бар электр тізбектерін қарастырайық.
1 сурет
Жоғарғы сұлбасын қарастырып, а және б түйіндер арасындағы тоқты, потенциал айырымын табамыз. Кедергілер және ЭҚК -тер мәндері берілген деп санаймыз.
Бұл есепті екіге бөлейік. Бірінші есепте екінші батареяны жоқ деп санаймыз, ал екінші есепте бірінші батарея жоқ деп санаймыз да, R кедергісінен өтетін тоқтарды табамыз. Бірінші батарея бар кездегі R кедергісінен I 1 тоқ өтсін делік, ал екінші батарея бар кездегі R кедергісінен I 11 тоқ өтсін делік. Сонда, егер екі батарея бар болған кезде толық тоқ осы екі тоқтардың қосындысына тең болу керек.
Кирхгофтың 1заңы:Электр тізбегінің түйініндегі токтардың алгебралық қосындысы нөлге тең . “ ┼ “ белгісімен түйінге кіретін “ ─ “ белгісімен түйіннен шығатын токтарды аламыз . 2, 4 суреттегі токтарды Кирхгоф заңы бойынша I 1 - I 2 - I 3 - I 4 = 0 деп жазамыз .
Кирхгофтың 1 заңы зарядтың сақталу заңының салдары болып есептеледі ; түйінге кіретін заряд саны түйіннен шығатын заряд санына тең, түйінде заряд - жинақталмайды және жойылмайды . Бұл заң тек түйінге ғана емес, тізбектің бөлігіне қолданылады .
Кирхгофтың 2 заңы:Тармақталған электр тізбегінің контурында әсер ететін ЭҚК алгебралық қосындысы осы контурдың барлық актив кедергілеріндегі кернеудің түсуінің қосындысына тең . Бұл теңдеуді қолдану үшін контурды айналу бағытын білуіміз керек . ЭҚК пен кернеу қосындыларын есептеу үшін “ ┼ “ белгісімен айналым бағытына сәйкес келетін ЭҚК мен кернеуді “ ─ “ таңбасымен ол бағытқа қарсыларын аламыз . Контур үшін Кирхгофтың 2 заңы
E 1 + E 2 - E 3 = - r 1 I 1 - r 2 I 2 + r 3 i 3
Ал енді есептеп көрелік. Екінші кернеу көзі жоқ болса, а нүктесінің потенциалын табайық.
Бірінші кернеу көзі жоқ болса, а нүктесінің потенциалын табайық.

 (3)
(3)
Екі батарея бар кездегі а нүктесінің потенциалы:
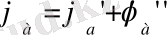 (4)
(4)
Сол сияқты б нүктесіндегі потенциалды табамыз:
 (6)
(6)
Енді R кедергісімен өтетін тоқ:
Мысалы 1 Суреттегі тізбек элементтерінің мәндері былай берілген болса:
R = 5 Om, R 1 = R 2 = 2Om, R 3 = 3 Om, R 4 = 4 Om, E 1 = 10 B, E 2 = 20 B.
.
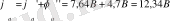 ,
,
Генератор әдісі.
Бұл әдіспен танысар алдында төмендегі электр сұлбасына көңіл аударайық.
2сурет
Мақсат: R - кедергісінен қандай тоқ өтетінін табу керек. Тәжірибе ретінде біз дәл сондай қернеу көзін теріс жалғайық.
3 сурет
Әрине бұл тізбек бойынша тоқ жүрмейді I = 0, себебі ортақ ЭҚК нөлге тең болады Е - E = 0. Ал 2 сурет бойынша тоқ қашан нөлге тең болады?
Әрине, егер R кедергісін алып тастасақ, онда бос жүріс болады. Ал R кедергісіне түсетін кернеу U бос - бос жүріс кернеуі деп атаймыз. R кедергісі жоқ кезде ішкі кедергісін табамыз R іш . Толық тізбектегі тоқ (2 cурет) төмендегідей табылады:
Сонымен егер генератор әдісімен пайдаланатын болсақ:
- Ізделінетін тоқ өтетін R кедергісін сұлбадан шығарып тастаймыз - үзік пайда болады (бос жүріс) .
- Бос жүріс кернеуін табамыз.
- ЭҚК - ін тұйықтаймыз да, ішкі кедергісін табамыз
- 9 - шы формула арқылы тоқты табамыз.
Мысал ретінде төмендегі есепті шығарайық.
4 сурет
Берілгені: R = 5 Om, R 1 = R 2 = 2Om, R 3 = 3 Om, R 4 = 4 Om, E 1 = 10 B,
E 2 =20B.
Табу керек: I R = ?
Екі батарея орнына бір батарея қоюға болады Е = - Е 2 + Е 1 = -20В + 10В =
=-10В.
- сұлбадан R кедергісін ажыратамыз.
- а нүктесінің потенциалын табамыз, б нүктесінің потенциалын табамыз.
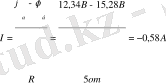
,
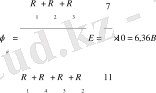

, .
3. Екі батареяны тұйықтаймыз.
Енді ішкі кедергіні табамыз:
Егер R кедергісін қайта қоссақ, одан өтетін тоқ
Жұлдызша жалғаудан үшбұрыш жалғауына көшу.
Төмендегі сұлбада жұлдызша жалғанған үш кедергіні қарастырайық.
1 сурет 2 сурет
Бірінші суретте 1, 2, 3, 0 нүктелер - түйіндер. Әр түйіннің өз потенциалы бар
I 1 + I 2 + I 3 = 0, (1)
енді осы тоқтарды потенциал арқылы жазайық:
(2) теңдеуді (1) теңдеуге ендірейік те,
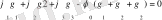 (3)
(3)
Сосын
2 суреттегі үшбұрышқа және белгілерімен
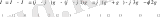 (5)
(5)
I
1
тоқ 1 суреттегі сұлбадағы және екінші суреттегі сұлбадағы I
1
тоғына тең болу керек. (5) - ші (4) - ші теңдеулерде
 - тердің коэффициент - тері бірдей болу керек
- тердің коэффициент - тері бірдей болу керек
Бұл формулаларда үшбұрыштың қабырғаларының өткізгіштері жұлдызшаның сәулелерінің өткізгіштеріне тең. (8) ді кедергі арқылы жазайық.
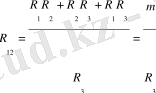 (9)
(9)

(12), (11), (9) теңдеулерін (10) - шы теңдеуге кіргізейік
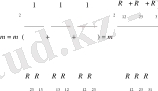 (13)
(13)
Осыдан,
(14) теңдеуді (9), (11), (12) теңдеулерге салсақ:
(15) - (17) теңдеулердің және (6) - (8) теңдеулердің структурасы бірдей.
Бұл теңдеулер түрлендіру теңдеулері деп аталады.
Айнымалы ток тiзбегiндегi актив кедергi. Кернеу мен ток күшiнiң әсерлiк мәнi
Тұрақты ток тiзбегiнiң заңдары айнымалы ток тiзбегi үшiн де орынды болады. Текбұлжағдайдағы
айырмашылық, айнымалы ток тiзбегiнде физикалық шамалар уақыттың өтуiмен байланысты өзгерiп отыратын болғандықтан, бұл заңдар сәйкес шамалардың берiлген уақыт мезетiндегi лездiк мәнi үшiн орындалады.
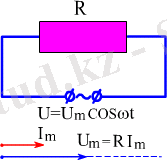
Айнымалы ток тiзбегiне қосылған R актив кедергiсiн қарастыралық ( 2. 5 - сурет ) . Егер бұл кедергiнiң ұштарына уақытқа байланысты
u = Um cos ωt (2. 10)
заңдылығымен өзгеретiн айнымалы кернеу берсек, онда Ом заңына сәйкес тiзбектегi ток күшiнiң лездiк мәнi
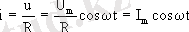
өрнегiмен анықталады. Мұндағы Im=Um/R ток күшiнiң амплитудалық мәнi. Бұл жерден ток күшiнiң де кернеу тәрiздi гармониялық заңдылықпен өзгеретiнi және тiзбектегi токтың фазасы кедергi ұштарындағы кернеудiң фазасына дәл келетiнi көрiнiп тұр. Кернеу мен ток күшi арасындағы осы байланысты мына жерден көруге болады.
Ендi осы тiзбекте бөлiнетiн қуаттың мәнiн табалық. Ол
тең. Яғни қуаттың лездiк мәнi де уақыттың өтуiне байланысты өзгерiп отырады екен. Ал оның орташа мәнi неге тең? Оны табу үшiн (2. 12) өрнегiнiң орташа мәнiн табу керек. Im және Um шамалары уақытқа қатысты өзгермейдi, ал уақытқа қатысты өзгерiп отырған косинустың квадратының бiр периодтағы орташа мәнi 1/2 - ге тең, онда сәйкес қуаттың орташа мәнi
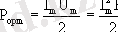
Бұл жерде егер
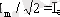 және
және
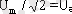 деп белгiлесек, онда қуаттың бұл өрнегi тұрақты ток тiзбегiндегi өрнекпен бiрдей болып шығады, яғни
деп белгiлесек, онда қуаттың бұл өрнегi тұрақты ток тiзбегiндегi өрнекпен бiрдей болып шығады, яғни
Осылай анықталған Iә және Uә шамаларын ток күшi мен кернеудiң әсерлiк мәндерi деп атайды.
Айнымалы ток тiзбегiндегi сыйымдылық
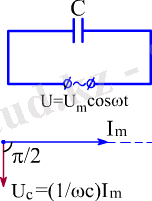
Айнымалы ток тiзбегiне жалғанған С сыйымдылығын қарастыралық ( 2. 6 - сурет ) . Конденсатордың астарларына
u = Um cos ωt (2. 15)
заңдылығымен өзгеретiн кернеу берiлiп тұрсын делiк. Онда осы тiзбектегi токтың мәнi қалай өзгередi? Оны табу үшiн алдымен зарядтың лездiк мәнiн анықталық. Ол мынаған тең:
q = Cu = CUmcos ωt (2. 16)
Тiзбектегi электр тогы конденсатор астарларындағы зарядтардың өзгеруiмен байланысты болғандықтан токтың әдеттегi анықтамасынан мынаны аламыз
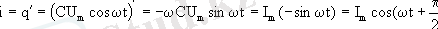
Бұл өрнек тiзбектегi ток күшiнiң уақытқа байланысты қалай өзгеретiнiн көрсетедi. Мұндағы Im=ωCUm шамасы - ток күшiнiң амплитудалық мәнi. Осы (2. 15) және (2. 17) өрнектерiн салыстыра отырып, тiзбектегi кернеудiң фазасы сәйкес токтың фазасынан π/2 - ге қалып отыратындығын байқауға болады. Кернеу мен ток күшi арасындағы бұл байланысты мына жерден көруге болады.
Тұрақты ток тiзбегiндегi Ом заңының өрнегiне ұқсас, айнымалы ток тiзбегiнде де кернеудiң амплитудалық мәнiнiң сәйкес токтың амплитудалық мәнiне қатынасы кедергiнi бередi, яғни
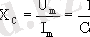
Оны сыйымдылық кедергiсi деп атайды. Сыйымдылық кедергiсi тұрақты шама емес, ол тiзбектегi айнымалы токтың жиiлiгiнен тәуелдi.
Ток пен кернеудiң арасында фазалар ығысуының салдарынан тiзбектегi бөлiнетiн қуаттың толық бiр период кезiндегi орташа мәнi нөлге тең болады.
Ом заңы
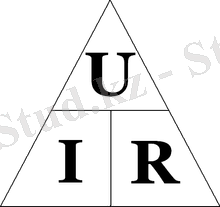 Ом заңын есте сақтауға көмек беретін сурет.
Ом заңын есте сақтауға көмек беретін сурет.
Ом заңы- электр тогының негізгі заңдарының бірі. Ом заңы - өткізгіштегі ток күшінің (І) осы өткізгіштің ұштары арасындағы кернеумен (U) байланысын анықтайды:
U=r*І (1)
мұндағы r өткізгіштің геометриялық өлшемдеріне, электрлік қасиеттеріне және температурасына байланысты болатын пропорционалдық коэффициенті r - омдық кедергі немесе өткізгіштің берілген бөлігінің кедергісі деп аталады. Ом заңын 1826 ж. неміс физигі Г. Ом (1787 - 1854) ашқан.
V - кернеу, I - ток күші, R - кедергі.
Жалпы жағдайда І мен U арасындағы тәуелділік - сызықты емес, бірақ кернеудің белгілі бір аралығында оны сызықтық деп есептеп, Ом заңын қолдануға болады; ал металдар мен олардың құймалары үшін бұл аралық іс жүзінде шектеусіз. (1) түрдегі Ом заңы ток көздері жоқ тізбек бөлігі үшін орынды. Тізбекте ток көздері (аккумуляторлар, генераторлар, т. б. ) болған жағдайда Ом заңы мына түрде жазылады:
rІ=U+ε (2)
мұндағы - қарастырылып отырған тізбек бөлігіне қосылған барлық ток көздерінің қорытқы электр қозғаушы күші. Тұйықталған тізбек үшін Ом заңы былай жазылады: rmІ=ε, (3) мұндағы толық кедергі (rm) сыртқы кедергі (r) мен ЭІК көзінің ішкі кедергісінің rі қосындысына тең: rm=r+rі . О. з-ның дифференциалды түрі өткізгіштің әрбір нүктесіндегі ток тығыздығын (j) электр өрісінің толық кернеулігімен байланыстырады: rj=Е+Еб немесе j=G(Е+Еб), (4) Бұл жерде r - өткізгіш материалының меншікті кедергісі, ал G=1/r - оның менш. электр өткізгіштігі, Е - потенциалды электр өрісінің, Еб - бөгде ток көздері тудыратын электр өрісінің кернеуліктері.
Айнымалы токтың толық тізбегі үшін Ом заңы
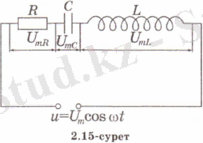
Бір-біріне тізбектей жалғанған , және кедергісіRрезистордан тұратын тізбектің қысқыштарына u = U m cosωt айнымалы кернеу түсірейік (2. 15-сурет) . Ток күшініңi лездік мәні де, I m амплитудалық мәні де тізбектей жалғанған тізбектің барлық бөлігінде бірдей болады. Ал ток көзінің полюстеріндегі лездік кернеу оның жеке бөліктеріндегі кернеудің лездік мәндерінің қосындысына тең:
u = u R + u C + u L . (2. 14)
Тізбектей жалғанған тізбектің барлық бөлігіндегі токтың тербелісі
i = I m cosωt
заңы бойынша өзгерсін.
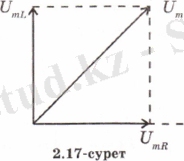
Қарастырып отырған тізбекте еріксіз электромагниттік тербелістер, яғни айнымалы ток пайда болады. Резистордағы, конденсатордағы және катушкадағы кернеудің амплитудаларын сәйкесінше U mR , U mC және U mL деп белгілеп, оларды векторлық диаграммаға салайық (2. 15-сурет) . Ток күшінің амплитудасын горизонталь ось бойымен бағытталған вектор түрінде кескіндейік. Онда горизонталь ось пен әрбір кернеу амплитудасы векторының арасындағы бұрыш ток күшімен ғана сәйкес кернеу тербелістерінің фазалық айырымына тең болады.
Активті кедергідегі кернеудің тербеліс фазасы ток күшінің тербеліс фазасымен сәйкес келеді, ал конденсаторда кернеудің тербелісі ток күшінің тербелісінен фаза бойынша π / 2-ге озады. Сондықтан (2. 14) өрнегін былай жазуға болады:
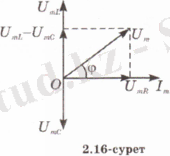
Түсірілген кернеудің
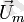 амплитудасын векторлардың қосындысы ретінде табуға болады, яғни
амплитудасын векторлардың қосындысы ретінде табуға болады, яғни
(кернеу белгісінің үстіндегі нұсқамаға (стрелкаға) қарап кернеуді векторлық шама деп қарауға болмайды. Бүл тек модульдері көрсетілген кернеулерге тең векторлар) . 2. 16-суреттен, барлық тізбектегі кернеудің амплитудасы Пифагор теоремасы бойынша
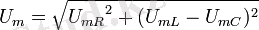
тең. Ом заңына сәйкес
U mL = I m X L , U mC = I m X C және U mR = I m R
Сондықтан
Осыдан
(2. 15)
Бұл айнымалы токтың толық тізбегі үшін Ом заңы.
X L = ωL
және
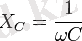
болғандықтан, (2. 15) формуласын былай жазуға болады.
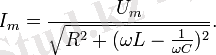
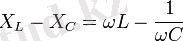
кедергісін реактивті кедергі, ал
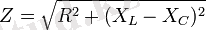
кедергісі айнымалы ток тізбегінің толық кедергісі деп аталады. ϕ фазалар айырымын векторлық диаграмманы колданып анықтауға болады:
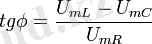
Немесе
(2. 16)
Ток пен кернеудің әсерлік мәндерін колдансақ, (2. 15) өрнегін былай жазуға болады:
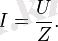
Тізбекте конденсатор жоқ кездегі векторлық диаграмманы салайық (2. 17-сурет) . Бұл дербес жағдайда
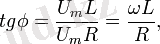
Егер (2. 15) пен (2. 16) өрнектерінде
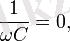
яғни
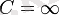
деп алсақ, соңғы екі формула шығады. Олай болса, тізбекте конденсатор жоқ болса, сыйымдылық C нөлге емес, шексіздікке тең екен. Шынында да, егер тізбектегі конденсатордың астарларын бір-біріне шексіз жақындатса, конденсаторды жоқ деп есептеуге болады. Ал жазық конденсатордың сыйымдылығы
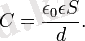
Бұл формуладан егер d = 0 болса,
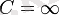
шығады.
Генератордан алынатын энергия тек активті кедергіде ғана жылу энергиясы түрінде бөлініп шығады. Реактивті кедергіде энергия жұтылмайды. Реактивті кедергіде периодты түрде электр өрісінің энергиясы магнит өрісінің энергиясына айналып, түрленіп отырады. Периодтың бірінші ширегінде, конденсатор зарядталып жатқанда энергия тізбекке электр өрісінің энергиясы түрінде түсіп, жинақталады. Ал периодтың келесі ширегінде, конденсатор разрядталып жатканда, энергия қайтадан магнит өрісінің энергиясы түрінде желіге қайтарылады.
Айнымалы ток тiзбегi үшiн Ом заңы
Бiр-бiрiмен тiзбектей жалғанған актив кедергiден, сыйымдылықтан және индуктивтi катушкадан тұратын айнымалы токтың толық тiзбегiн қарастыралық.
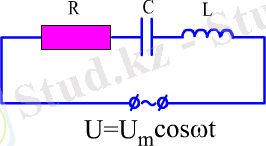
Егер осы тiзбектiң ұшына жиiлiгi ω, ал амплитудасы Um-ға тең бола отырып гармониялық заңдылықпен өзгеретiн айнымалы кернеуiн берсек, онда бұл тiзбекте
I = Imcos ωt (2. 23)
заңдылығымен өзгеретiн ток күшiнiң ерiксiз тербелiсi пайда болады. Ендi осы ток күшi мен кернеудiң тербелiсi амплитудаларының арасындағы байланысты, басқаша айтқанда осы айнымалы ток тiзбегi үшiн Ом заңын табалық.
Тiзбектегi толық кернеудiң лездiк мәнi осы тiзбектiң әрбiр бөлiгiндегi кернеулердiң түсуiнiң қосындысына тең, яғни
Тiзбектегi толық кернеудiң амплитудасын оның бөлiктерiндегi кернеулердiң амплитудалары арқылы өрнектеу үшiн векторлық диаграмма деп аталатын әдiстi қолдану ыңғайлы.
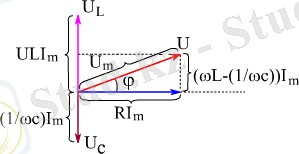
Бұл әдiс тiзбек бөлiктерiндегi кернеулердiң фазаларының әртүрлi екенiн ескеруге мүмкiндiк бередi. Диаграмманы тұрғызу барысында алдымен тiзбектегi токка сәйкес бағытты таңдап алады да соған қатысты кернеулердiң амплитудалық мәндерiн олардың фазалар айырымын ескере отырып салады. Осылай тұрғызылған диаграмма 2- суретте келтiрiлген. Бұл суреттен тiзбектегi толық кернеудiң амплитудасы (үшбұрыштар үшiн Пифагор теоремасын пайдаланғанда)
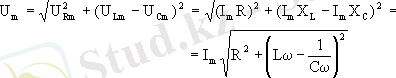
екенi көрiнiп тұр.
Бұл өрнектегi
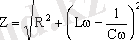
шамасы тiзбектiң толық кедергiсi болып табылады.
Векторлық диаграммадан кернеу тербелiсiнiң фазасы ωt + φ екенi көрiнiп тұр. Сондықтан, кернеудiң лездiк мәнi
Ал кернеу мен токтың лездiк мәндерiнiң арасындағы фазалар айырымы
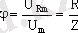
Айнымалы ток тiзбегiндегi қуаттың лездiк мәнi p = I2R = ImR cos2ωt. Бiр тербелiс периоды кезiндегi cos2ωt функциясының орташа мәнi 1/2 болғандықтан тiзбектегi қуаттың орташа мәнi
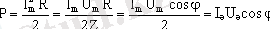
Айнымалы ток тiзбегiндегi резонанс
Айнымалы ток тiзбегiнiң ( 2 - сурет ) толық кедергiсi (2. 27) өрнегiне сәйкес тек тiзбек элементтерiнiң параметрлерiнен ғана емес, сонымен қатар мәжбiрлеушi кернеудiң өзгеру жиiлiгiнен де тәуелдi. Яғни, жиiлiк өзгерген кезде толық кедергi де өзгередi. Тiзбектегi ток максимальдi болу үшiн, Ом заңына сәйкес, оның толық кедергiсi минимальдi болуы керек. Ал (2. 27) өрнегiнен толық кедергiнiң мәнi
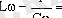
шарты орындалғанда минимальдi болатыны көрiнiп тұр. Бұл шартқа сәйкес келетiн сыртқы мәжбiрлеушi кернеудiң жиiлiгi
Ал бұл еркiн тербелмелi контурдың өшпейтiн еркiн тербелiсiнiң жиiлiгiне тең шама.
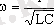
Олай болса, сыртқы мәжбiрлеушi кернеудiң жиiлiгi тербелмелi контурдың еркiн тербелiсiнiң жиiлiгiне сәйкес болғанда тiзбектегi токтың мәнi күрт артып кетедi екен. Осы құбылысты айнымалы ток тiзбегiндегi резонанс құбылысы деп атайды. Тiзбектiң актив кедергiсiнiң әртүрлi мәндерiндегi токтың амплитудалық мәнiнiң сыртқы мәжбiрлеушi кернеудiң жиiлiгiнен тәуелдiлiгi келтiрiлген. Электр тiзбегiндегi резонанс құбылысы радиотехникада, оның iшiнде қабылдау схемаларында, күшейткiштерде, жоғарғы жиiлiктегi тербелiс генераторларында кеңiнен қолданылады.
Контурлы тоқ.
Төмендегі электр сұлбасына көңіл бөлелік. Белгілі кедергілер және кернеу көздер барда; түйінге келетін және шығатын тоқтардың шамасын табу керек.
1 Сурет. I’, I’’ - Контурлы тоқтар.
Екі тұйық контурларда бір ғана контурлы тоқ жүреді I’ және I’’. Әр тұйық контурға Кирхгофтың екінші заңын жазайық:

Осы теңдеулер жүйесін шешіп, контур тоқтарын табамыз.
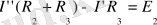
Контур тоғы
Екі түйін әдісі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz